混合型货物作业点取送车作业优化通用模型及算法

郭垂江，孙小月，陈 韬，陈春晓，陈钉均

（1.成都信息工程大学 物流学院，四川 成都 610103；2.西南交通大学 交通运输与物流学院，四川 成都 610031；3.湖南铁道职业技术学院 轨道交通运营管理学院，湖南 株洲 412001）

我国普速铁路大部分车站需办理货运业务，因而衔接了货场、专用线等货物作业点，调车机车（后文简称为“调机”）需往返车站与货物作业点间进行取送调车作业。按照车站与各货物作业点间连线形成的平面图的形状，货物作业点的布置形式可分为放射形、树枝形和混合型3种，我国铁路车站货物作业点的各种布置形式中，混合型的占比最大[1]。

针对放射形货物作业点取送作业计划编制的研究相对比较充分，有运用排序理论[2]针对车辆整列到发的直达车流取送车作业问题的研究，有以货车在站总停留时间最小为优化目标针对非直达车流取送车作业问题的研究[3]，也有研究建立了能同时描述直达车流和非直达车流的数学模型[4]。针对树枝形货物作业点的研究中，目前在车站取送作业计划编制方面的既有方法多是将其转化为哈密尔顿图最短路问题[5−9]，也有个别方法利用了排序理论[10]；部分学者将树枝形货物作业点车辆取送的顺序、批次划分作为1个系统进行优化[11−13]，推进了结合铁路生产实际研究取送作业计划优化理论的进程。树枝形货物作业点取送车作业的优化目标一般为最小化所有车辆在站停留车小时和最小化调机走行距离2类，也有学者基于这2类目标建立了多目标优化模型[14−15]。但到目前为止，还没有针对混合型货物作业点取送车作业优化方面的成果，更没有考虑进路约束条件，能兼容车组整列和分散到发、可适应不同作业类型的混合型货物作业点取送车作业计划优化的通用模型。

本文以最小化计划时段内机车走行时间和等待时间为优化目标，考虑不同货物作业点间调移作业所要求的调机访问先后次序、同一货物作业点车组先送后取、调机牵引能力限制、货物作业点容车数、批次作业的开始时分及结束时分等约束，建立货物作业点取送车作业优化的通用模型；采用模拟退火算法作为主函数对模型进行求解；以岳阳南站为例对模型及算法进行验证。

1 问题描述及假设

1.1 问题描述

阶段计划规定了本阶段应进行取送作业的货物作业点及车数。混合型货物作业点取送车作业优化是指：针对混合型布置的作业点，对其阶段计划涉及的取送车作业，给出作业批次、顺序和时分的具体优化安排，使调机能够高效率地完成规定的取送车作业任务。

我国铁路车站的货物作业点绝大多数是从车站两端咽喉处接轨。因线间距相对到发线（或调车线）长度短得多，因此1个典型的具有混合型货物作业点的车站平面示意图可以简化为图1。由图1可知：总体来看所有货物作业枝呈放射形分布，但就某个分枝细部而言，又呈树枝形分布；若车站每条货物作业点枝只有1个货物作业点，则该混合型货物作业点则可认为是放射形货物作业点；若车站只有1条货物作业点枝，且该货物作业点枝上的货物作业点数量大于1个，则该车站的混合型货物作业点可认为是树枝形货物作业点。因此，可认为放射形和树枝形货物作业点是混合型货物作业点的特殊形式，本文对混合型货物作业点取送车作业的研究成果，同样也适用于放射形和树枝形货物作业点。

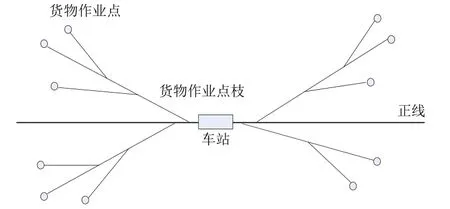
图1 混合型货物作业点示意图

1.2 设定条件

（1）不同车辆视为同一取送车组的条件为：解体完毕时分相同；同一批次送往同一地点进行货物装卸车作业，或从同一装卸点取车且被编入同一列出发列车。

（2）同一批次调机对同一货物作业点只访问1次。

（3）已知各车组所在列车的解体完毕时分、装卸作业完毕时分，以及各车组所编入列车的编组开始时分。

（4）已知挑选车组时间、对货位时间、调机在各货物作业点（车站）间走行时间、各车组的货物作业时间。

（5）已知各货物作业点车辆容纳能力和各货物作业点在计划阶段内需取送车数。

（6）车站只配置了1台调机担当取送车作业任务。

（7）调机牵引能力已知，调机走行速度不受调机所连挂车辆数量的影响。

（8）调机将车组送至货物作业点后随即离开，无须等待装卸作业完毕。

（9）接发列车作业可能妨碍的调车作业进路仅指穿越正线的调车进路，并且不考虑进路分段解锁，即认为接发列车进路一次办理、一次解锁。

2 模型建立

2.1 符号定义

1）参数符号

N为车站货物作业点数量，个；i，i'，i″，i″'为车站和货物作业点的序号，均取为0，1，2，…，N；vi，vi'，vi''和vi'''为车站和货物作业点 （其中v0为铁路车站）；K为车站货物作业点枝的数量，条；k，k'为货物作业点枝序号，均取为1，2，…，K；Uk和Uk'为货物作业点枝，表示相应的货物作业点集合。

tii'为包含了挑选车组时间、对货位时间在内的货物作业点（车站）vi至货物作业点（车站）vi'的调机走行时间，min；ttraverse为调机穿越正线所需要的时间，min；W为计划时段内列车运行图规定可用的调车时间窗数量，个；…，W为调车时间窗，即为能够保证穿越正线调车作业的列车间隔时间，min；τ0为计划阶段的开始时分；为货物作业点vi装卸作业完毕时分；为需到货物作业点vi进行装卸车组的解体完毕时分；为货物作业点vi的作业车组所编挂的列车的编组开始时分。

l（l=1，2，3）表示车组的取送作业模式：送车时l=1；取车时，若车组为计划阶段内到达的车组则l=2，车组为计划阶段前货物作业点结存的车组则l=3。Ri为货物作业点vi的容车数，辆；Q为调机的最大牵引辆数，辆；为调机前往作业点枝Uk上货物作业点vi需进行类型l的调车作业；为取送调车作业对应的车组；M为足够大的正数。

2）变量符号

定义如下中间变量：γ0i和γi0均为0-1变量，分别表示调机从车站v0驶向货物作业点vi、从货物作业点vi驶回车站v0时是否要穿越正线，若需穿越正线则取1，否则取0；μii'为0-1变量，若从作业点枝Uk上货物作业点vi的取车作业和从作业点枝Uk'上货物作业点vi'的送车作业为同一车组（即） 则取1，否则取0；ηki为0-1变量，若从作业点枝Uk上货物作业点vi的取车和送车作业为同一车组（即） 则取 1，否则取 0；为调车作业在解中的序号；J为解的批次数量，批；j为解批次的序号，j=1，2，…，J；Vj为批次j的作业点集合；为第j批从货物作业点（车站）vi转移至货物作业点（车站）vi'车组的货车数，辆；为货物作业点枝Uk上货物作业点vi在第j批次作业前的现有货车数，辆。

2.2 优化目标

每批调机取送车时间是指每批次作业时，自调机离开车站时起，至完成该批次取送作业任务后返回车站止所延续的时间，而调机取送车总时间为阶段内所有批次调机取送车时间之和。所有批次调机取送车总时间越少，意味着调机作业效率越高。

调机取送车作业总时间由各批次调机在货物作业点（车站）间的总走行时间t走行、调机到达货物作业点时由于车辆未装卸完毕需等待的总时间t等待和接发列车对调车作业的总影响时间t影响组成。其中：t等待指机车到达货物装卸地点时起，至车辆已经装卸完毕、装卸机具已经撤离，具备取车条件时止调机等待的非生产时间；t影响指各批次调机返回车站时由于相关列车工作正在进行而影响的取送车作业时间。因此，混合型货物作业点取送车作业优化模型的优化目标Z为

其中，

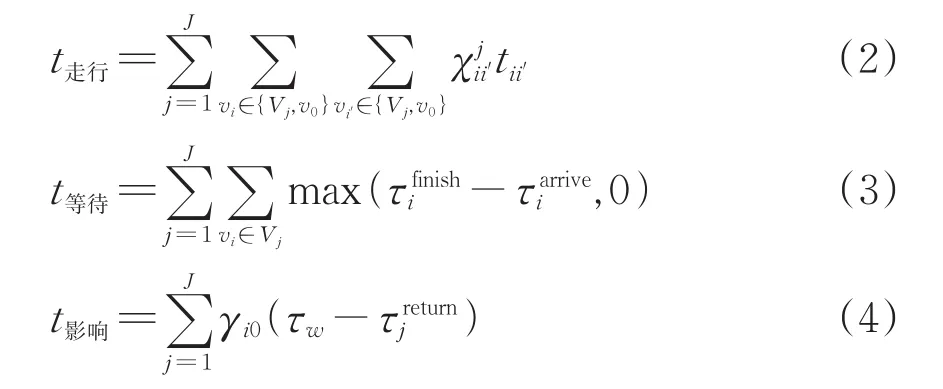
需要说明的是：若调车进路与接发列车进路存在时空冲突或调车时间窗剩余时间不足以完成调机穿越正线作业，调机必须在相应的防护信号机前停轮等待至接发列车作业完毕后才能利用正线空闲时间间隔（调车时间窗）继续进行作业；某批次取送车时，调机需从车站驶向货物作业点，或从货物作业点返回车站；若调机在不同货物作业点枝上的货物作业点间走行，也需先从货物作业点返回车站，再驶向另1个货物作业点；调机从车站v0驶向货物作业点时，若存在进路冲突的接发列车作业正在进行，将本批次的调车作业开始时分推后即可疏解；但调机返回车站v0时，若存在进路冲突的接发列车作业正在进行，调机必须在相应防护信号机处等待接发列车作业完毕后才能继续进行。

2.3 约束条件

1）调移作业要求的调机访问次序约束

双重货物作业车需从卸车货物作业点调移至装车作业点。调机必须先访问卸车作业点取出空车，然后才能访问相应的装车作业点送车，即取送车作业时应满足调机访问货物作业点的优先次序约束，有

2）同一货物作业点同一车组先送后取顺序约束

在车组的1次取送作业中，需按顺序完成送车、装卸、取车等作业。因此对某个货物作业点的车组而言，取车作业必定在送车作业之后，则任一车组在同一货物作业点作业应满足“先送后取”的作业顺序关系，即

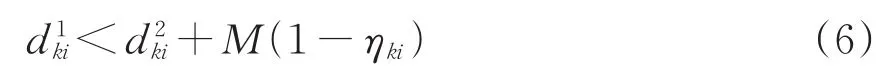
3）调机牵引能力限制约束

调机牵引能力会影响取送车作业的批次划分，即同样的调车作业任务，功率小的调机可能需要较多的作业批次。调机连挂车辆数量受调机能力的限制，每一批次调车作业过程中调机所连挂的车辆数不能超过其最大牵引能力，否则将造成调机启动和制动困难。因此，调机连挂车数量应满足调机牵引能力限制约束，即

4）货物作业点容车数约束

货物作业点容车数的大小也会影响到取送车作业的批次划分，并且货物作业点货位容车数是有限的。因此在任何时间货物作业点的现有车数都不能超过该货物作业点的容车数，即

5）批次作业开始时分约束

每批次作业中，送往货物作业点的车辆只能从送车前已经到达车站且解体完毕的车辆中选择。因此每批含有送车的取送车作业开始时分不应早于所有送车组的解体完毕时分，即

每批次取送车作业的开始时分不应早于上一批次的取送车完毕调机返回调车场（车站）的时分，即

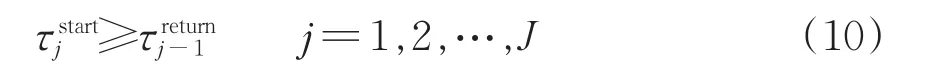
第1批次取送车作业开始时分不应早于计划阶段的开始时分，即

若本批次的首项取送车作业需要跨越正线，则本批次的开始时分应在调车时间窗内，且应在调车时间窗内完成跨线作业，即

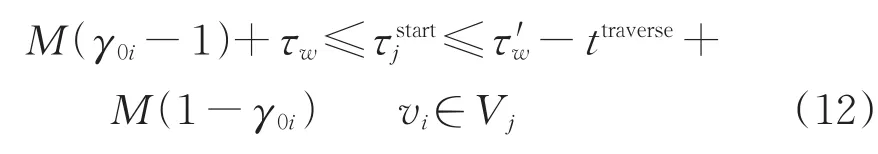
6）批次作业结束时分约束

车辆取回车站的时分应不大于车辆最晚编组开始时分，否则将造成出发列车晚点或由于编入计划外列车造成车辆在站停留时间的延长，即

3 求解方法

建立的铁路车站混合型货物作业点取送车作业优化模型，是1个需对取送车作业批次划分、作业顺序、作业时间3个变量进行决策的问题，选用模拟退火算法作为算法主函数，将约束条件作为子函数，嵌入算法判断解是否可行，并进行搜索求解。

3.1 算法主函数

模型求解时，考虑调移作业要求的调机访问次序约束式（5）、同一货物作业点同一车组先送后取顺序约束式（6）规定了调机访问相应货物作业点的次序关系，因此归为一类，运用取送作业逆序判断及处理函数进行判断和处理；调机牵引能力限制约束式（7）、货物作业点容车数约束式（8）会影响计划阶段内作业任务的批次划分，因此运用批次划分函数和批次作业车数判断函数进行判断和计算；批次作业开始时分约束式（9）—式（12）和批次作业结束时分约束式（13）是取送车作业的时间约束，限定了取送作业的时间范围，因此归为一类，运用取送作业时间计算函数进行判断和计算。

混合型货物作业点取送车作业优化模型属于最小化问题，其目标函数Z可直接作为解S质量的评价函数。采用文献[9]的邻域解构造方法，依次运用卸车点位置前后移动、装车点位置前后移动和2-交换方法构建新的邻域解。由此设计模型的求解算法步骤如下[16−18]。

步骤1：输入初始温度T0、温度下降率λ、终止条件ε和马尔科夫链L，运行取送作业逆序判断及处理函数，生成1个满足调机访问次序关系初始可行解S0。

步骤2：对当前温度T=Tp，令q=1。

步骤3：根据邻域解构造规则建立当前解S的邻域NS，随机产生1个满足调机访问次序关系的邻解S'。

步骤4：执行批次划分函数和批次作业车数判断函数，判断邻解的可行性，若可行，执行取送作业时间计算函数，计算ΔZ=ZS'−ZS。

步骤5：若ΔZ≤0或exp(ΔZ/T)＞rand(0，1)，则接受S'作为新的当前解，即S=S'；否则保留当前解S，令q自增1，若q=L，转步骤6；否则转步骤3。

步骤6：根据温度衰减函数Tp=λTp−1下降温度，若Tp≤ε，转步骤7；否则转步骤2。

步骤7：输出满意的取送车调车作业批次划分、顺序及具体作业时分，计算结束。

3.2 解的表示

对每1项调车作业glki分配1个唯一的数字编号su，u=1，2，…，U（su为对应的取送车调车作业的作业序号；U为在整个计划阶段调车作业的总项数），这样调车作业可与数字编号一一对应，这串自然数s1，s2，…，sU便可用于表示模型的解S。

3.3 取送作业逆序判断及处理函数

取送作业逆序判断及处理函数计算步骤如下。

步骤1：输入解S=s1，s2，…，sU，令u=1。

步骤2：若当前作业su为送车作业，与前面取车作业车组相同，且作业点位置相同，则交换解中2个作业的位置；否则保持作业su位置不变，并令u自增1。

步骤3：若当前作业为取车作业，与前面送车作业车组相同，但作业点位置不同，则交换解中2个作业的位置；否则保持作业su位置不变，并令u自增1。

步骤4：若u≤U，则转步骤2；否则输出处理后的解S'，计算结束。

3.4 批次划分函数

批次划分函数计算步骤如下。

步骤1：输入解S=s1，s2，…，sU，令u=1，当前解的批次数j=1。

步骤2：若当前作业放射枝与上一项作业放射枝不同，令j自增1；否则j=j，并令u自增1。

步骤3：若u≤U，则转步骤2；否则，输出批次数J=j，计算结束。

3.5 批次作业车数判断函数

批次作业车数判断函数计算步骤如下。

步骤1：输入解S=s1，s2，…，sU，令j=1。

步骤3：在该货物作业点前将作业拆分成2个批次，重新记录各批次序号及规模，转步骤1。

步骤4：若j≤J，则转步骤2；否则，输出批次数J，计算结束。

3.6 取送作业时间计算函数

以调机离开车站的时分为批次作业的开始时分，完成相关作业后返回车站的时分为批次作业的结束时分，那么确定取送作业时间的关键是确定每个批次的开始时分。首先运用式（9）—式（12）计算每批次作业的允许开始时分，再结合每个批次最迟返回车站时分vi∈Vj反推每个批次最迟开始时分。

取送作业时间计算函数的计算步骤如下。

步骤1：输入解S=s1，s2，…，sU，令j=1。

步骤3：计算本批次第1个货物作业点调机到达货物作业点的时分调机到达其他货物作业点vi的时分调机离开货物作业点vi的时分进而确定各批次车组返回车站的时分若本批次返回车站需跨越正线则，否则。

步骤5：若j≤J，则转步骤3，否则输出所有批次取送车调车作业总时间计算结束。

4 案例分析

选取岳阳南站对提出的模型及算法进行测试。岳阳南站平面示意图如图2，衔接铁路货场、专用线货物作业点枝6条，货物作业点15个，各货物作业点情况见表1。货物作业点枝1和点枝2处在车站第Ⅰ象限，货物作业点枝3和点枝4处在车站第Ⅲ象限，货物作业点枝5和点枝6处在车站第Ⅳ象限。调车场由9道、11道、13道和15道组成，与货物作业点枝1和点枝2同处于车站正线一侧。调机牵引能力为40辆，调机穿越正线所需要的时间为5 min。

图2 岳阳南站平面示意图

表1 岳阳南站货物作业点情况

选定具有代表性的某日6：00—9：00计划阶段内的取送车调车作业任务进行测试，作业任务表见表2。该计划阶段内，化肥厂线的7辆车需调移至小港线进行装车，6：00时现存的车情况为：氮1线10辆、磷1线10辆、磷2线11辆、化肥厂线7辆、洪湖线15辆、协作线8辆、南1线10辆和南2线8辆。计划阶段内可用调车时间窗为[6：00，6：35]，[6：55，7：40]，[7：53，8：09]，[8：22，9：00]。以时分0：00为0，将1 d内时间转化为[0，1 440]中的对应数字进行计算。

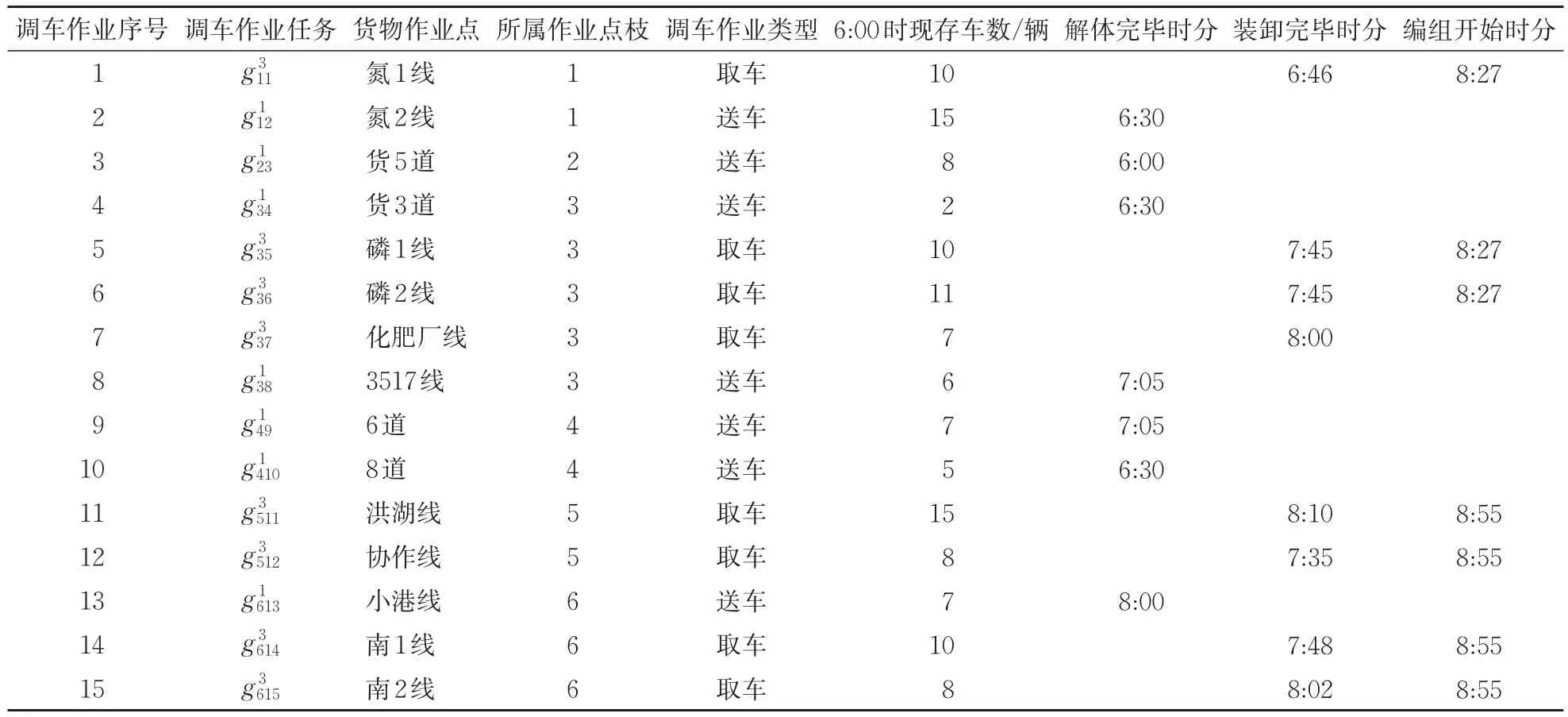
表2 某日6：00—9：00计划阶段内取送车调车作业任务

调机的平均走行速度取5×102m·min−1（即30 km·h−1），挑选车组时间取2 min，对货位时间取1 min。马尔科夫链L=50，初始温度T0=1×106，终止条件ε=1×10−3，温度下降率λ=0.99。运用MATLAB7.0在PC AMD2.20GHZ计算机上进行编程辅助计算，每次测试所得到的结果不尽相同，平均目标函数值为110 min。算法收敛平均时间为10 s左右，能满足铁路车站现场取送车调车作业计划编制的时间要求。选取1个满意解为：该满意解的取送车调车作业安排如图3所示，对应的货物作业点取送作业时分见表3。

图3 满意解的取送车调车作业安排

表3 满意解的各取送车调车作业时分

所有作业分7批次进行，各批次作业时分见表4。目标函数值Z*=107 min，总等待时间t等待=8 min，总影响时间t影响=0 min，较好地规避了本阶段列车接发对取送车调车作业的影响，说明本文所提出的模型和算法是可行的和有效的。此案例包括了货物作业点取车、送车、取送结合、作业点间调移等作业形式，具有广泛的代表性，因此本文所提的模型及算法是通用的。

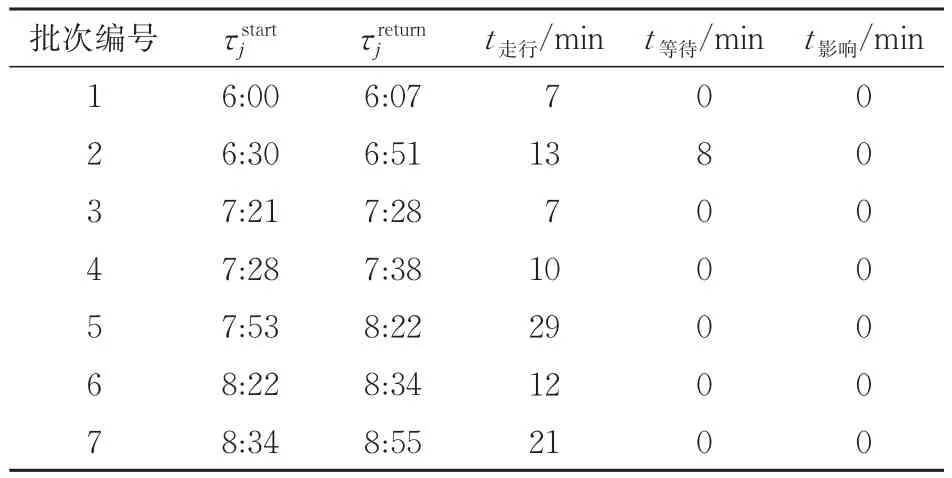
表4 满意解的各批次作业时分及优化效果

5 结 论

（1）因车组整列到发是分散到发的特殊情形，所以提出的模型适用于计划阶段内车组整列或分散到发的所有情景。

（2）因单一取车、单一送车、送车兼调移、取车兼调移、取送车作业结合是送调取结合作业的特殊形式，所以提出的模型适用于以上所有取送车调车作业形式。

（3）模型目标函数增加了调机等待装卸时间和接发列车对调车作业的影响时间，考虑了的约束条件包括：调移作业要求的调机访问次序、同一货物作业点车组先送后取、调机牵引能力限制、货物作业点容车数、批次作业开始时分和批次作业结束时分，所编制的取送车调车作业计划较以往研究更具有可行性。

（4）案例包括了货物作业点取车、送车、取送结合、作业点间调移的等多种作业形式，计算结果表明，模型能较好地对计划阶段内具有多种形式的取送车调车作业做出安排，总等待时间8 min，总影响时间为0 min，较好地规避了本阶段列车接发对取送车调车作业的影响。算法效率能满足铁路车站现场取送车调车作业计划编制的时间要求，因此本文所提出的模型和算法是可行且有效的。