关于m幂等矩阵秩的性质研究

王 慧

(淮北师范大学 数学科学学院，安徽 淮北 235000)

0 引言

设Fn×n为数域F上所有n阶矩阵的集合，r(A)为矩阵A的秩，E为单位矩阵，Z表示整数集合，Z+表示正整数集合.设A∈Fn×n，m∈Z+，且m≥2，若Am=A，且Ak≠A(k=2,3,…,m-1)，则称A为m幂等矩阵.m幂等矩阵是高等代数中的重要概念之一，矩阵的秩是刻画矩阵的一个重要的数字特征，与矩阵的秩有关的命题又是判断m幂等矩阵的重要条件，因而对矩阵秩的研究一直是一个有意义的课题.近年来，相关研究成果有：利用矩阵的秩和齐次线性方程组解空间的维数，给出了m幂等矩阵的新等价条件[1]；采用五种方法证明了关于幂等矩阵秩的一个命题，并进行了推广[2]；杨忠鹏等给出了m幂等矩阵秩的一种等价刻画[3].本文将从三个不同方面出发，证明关于m幂等矩阵秩的一个重要结论.

首先给出几个矩阵秩的性质及引理.

性质1已知A∈Fm×n，B∈Fm×n，则r(A+B)≤r(A)+r(B).

性质2若n阶矩阵A，B满足AB=O，则r(A)+r(B)≤n.

性质3已知A∈Fm×s，B∈Fs×n，则r(A+B)≤min{r(A),r(B)}.

引理1 已知A∈Fm×n，B∈Fm×n，C∈Fm×n，有

引理2 (Schur公式)设A∈Fr×r，B∈Fr×(n-r)，C∈F(n-r)×r，D∈F(n-r)×(n-r)，且方阵A，D均可逆，则

利用Schur公式，可得引理3.

引理3 (1)若方阵A，D均可逆，则

(2)若A，B，C，D均为n阶方阵，且|A|≠0，AC=CA，则

引理4设A∈Fm×n，r(A)=r,则存在列满秩矩阵Lm×r与行满秩矩阵Hr×n，使A=LH.

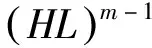
证明(充分性) 已知A=LH，则

由Lm×r是列满秩矩阵，Hr×n是行满秩矩阵，因而

r((HL)m-1-Er)=r(L((HL)m-1-Er)H)=O，

即(HL)m-1=Er.

1 定理及证明

定理1 设A∈Fn×n，m∈Z+，且m≥2，则Am=A的充分必要条件是r(A)+r(E-Am-1)=n.

证法1 利用矩阵的等价标准形

(充分性) 设r(A)=r，则

r(E-Am-1)=n-r，

(1)

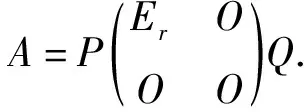
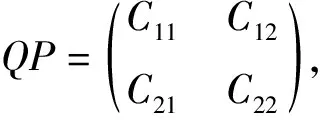
从而

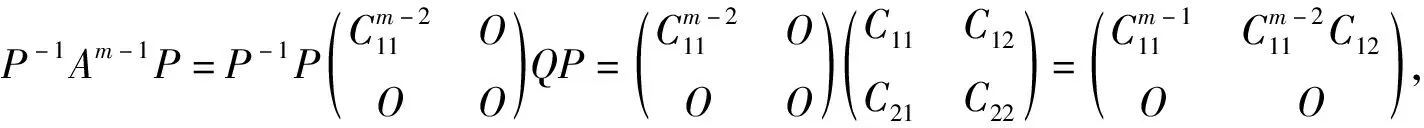
(2)

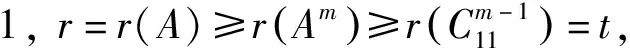
(必要性) 由Am=A得，A(E-Am-1)=O，由性质2知，

r(A)+r(E-Am-1)≤n；

(3)

由性质2、3得，

r(A)+r(E-Am-1)≥r(Am-1)+r(E-Am-1)≥r(Am-1+E-Am-1)=r(E)=n，

(4)

从而，由(3)(4)两式得，r(A)+r(E-Am-1)=n.

证法2 利用矩阵的满秩分解

根据引理1，记A=LH，其中L为n×r列满秩矩阵，H为r×n行满秩矩阵，构造n+r阶分块矩阵，则

由引理3(1)，得

即

n+r(Er-(HL)m-1)=r+r(En-(LH)m-1)，

亦即

n+r(Er-(HL)m-1)=r(A)+r(En-Am-1).

(5)

由(5)式可知，r(A)+r(En-Am-1)=n的充分且必要条件是r(Er-(HL)m-1)=0，即Er=(HL)m-1.由引理4知，r(A)+r(En-Am-1)=n的充分且必要条件是Am=A.

证法3 利用分块矩阵的初等变换

即

(6)

即上述两个分块矩阵均可逆.从而由引理5及性质4，知

故Am=A的充分必要条件为

r(A)+r(E-Am-1)=n.

2 结语

矩阵的秩是矩阵理论中的一个重要概念，是矩阵的重要数量特征，本文主要从矩阵的等价标准形，满秩分解及分块矩阵的初等变换三个不同方面，证明了m幂等矩阵秩满足的一个充要条件，该条件是高幂等矩阵秩的性质的一个补充和完善.