γ能谱符合相加效应修正方法及影响因素
张磊
γ能谱符合相加效应修正方法及影响因素
张磊
(上海市辐射环境安全技术中心 上海 200065)
在辐射环境质量监测中,多能核素的级联符合相加效应是影响γ能谱活度测量准确性的重要因素之一,为了提高待测样品分析的准确性,对结果进行符合相加修正是十分必要的。以152Eu核素为例,根据峰总比不变性特点,获得探测器峰总比拟合公式,联合符合相加修正公式,全能峰效率公式,计算了152Eu核素的符合相加修正因子,进一步采用Genie 2000符合相加蒙特卡罗程序对液体体源的152Eu核素进行了符合相加修正。点源的修正结果与真值的相对偏差小于6%,体源修正结果与真值的相对偏差在±4%以内。通过点源符合相加修正因子与源到探测器距离的线性关系,可以得到符合相加效应可忽略的最小测量距离;体源样品的符合相加修正结果表明:同一介质的样品,高度越高,符合相加修正因子越小;自吸收效应会在低能端对样品的有效立体角产生较大影响,从而影响样品的符合相加修正因子。峰总比不变性与衰变纲图相结合的数值修正方法,不需要对不同位置处的点源总效率进行测量,与蒙特卡罗程序法相比,该方法无需对探测器进行工厂表征,不用对体源介质、密度和形状等参数进行描述;舍弃级联符合较严重的能量点后,可用于环境应急样品的符合相加修正。
符合相加修正, γ谱仪,峰总比
半导体和闪烁体γ能谱仪在测量样品中多能量核素的放射性活度时,会产生对测量结果影响比较大的符合相加效应[1]。符合相加效应是指核素发射的级联γ光子产生的级联辐射有可能在探测器内同时被探测而记录为一个事件,使实际测量的有关γ射线全能峰面积增加或减少的现象。实际测量面积增加或减少都会影响测量结果的准确性,所以需要对活度结果进行符合相加修正。
国内外对γ能谱的符合相加修正方法都有相关研究。谭金波、苏琼、何宗慧等[2‒4]给出了符合相加修正数值计算的通用公式;Morel等[5]给出了含内转换系数的符合相加修正的数值表达式;Rizzo等[6]通过矩阵数值方法对多能核素的符合相加修正进行了研究,对体源的符合相加修正引入了“有效全能峰效率”的表达式;Necati等[7]利用EGS4蒙特卡罗程序包对134Cs核素点源的符合相加修正进行了验证,修正结果与真值的相对偏差在5%以内;Giubroned等[8]利用GEANT4蒙特卡罗程序对88Y和60Co的符合相加效应进行了修正计算,从而获得了无符合相加的体源全能峰效率曲线;文献[9]利用LABSOCS、ANGLE3和GESPECOR等蒙特卡罗程序对食品样品进行了符合相加修正模拟,验证了这三个程序对食品基质活度测量的有效性。除了上述数值计算方法和蒙特卡罗程序方法外,还有距离法和单能效率法。距离法即通过提高待测样品到探测器的距离,来减少级联符合相加影响。单能效率法[10]就是采用一套单能γ标准源,通过拟合得到一条无符合相加效应的全能峰效率曲线,再制备一个含多能测核素的标准源,获得有符合相加影响的全能峰效率曲线,两者的比值就是符合相加修正因子。前述国内外文献均以讨论符合相加修正的方法为主,很少涉及探测器大小、样品尺寸以及介质密度等因素对符合相加效应的影响情况。
以级联符合比较多的152Eu核素为例,用数值计算法和蒙特卡罗程序法分别计算了点源和体源的符合相加修正因子,提出了将探测器峰总比不变性与衰变纲图相结合的符合相加修正方法,并验证了该方法的准确性,重点讨论了点源符合相加效应的影响因素,及体源几何尺寸和介质密度等对符合相加效应的影响程度。
1 仪器及标准物质
符合相加修正实验使用的是美国堪培拉公司生产的GC 4019型P型高纯锗探测器,晶体直径6.1 cm,晶体到探测器表面的距离0.5 cm,分辨率(@1.33 MeV)≤1.9 keV,峰康比≥60∶1,峰型参数十分之一全高宽(Full Width at Tenth Maximum,FWTM)/半高宽(Full Width at Half Maximum,FWHM)≤1.9,相对探测效率为42%,高压为+2 000 V,采用铝壳封装。
实验待测点源的生产厂家为美国Eckert & Ziegler公司,规格为⌀25 mm×3 mm,152Eu点源吸附在直径约为1 mm的离子交换小球上,肉眼可见;液体标准源的生产厂家同样为美国Eckert & Ziegler公司,几何尺寸为⌀75 mm×70 mm,密度为1.02 g∙cm-1,该标准源内含有241Am、109Cd、57Co、139Ce、51Cr、85Sr、137Cs、54Mn、65Zn、60Co、88Y等放射性核素,核素的能量覆盖了低、中、高能。
2 方法与实验
2.1 活度公式
活度公式如下:


2.2 符合相加修正公式






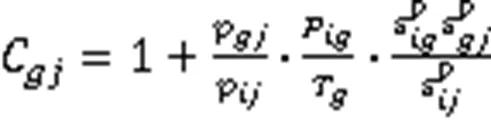
如果探测器低能端的能量低于50 keV,就需要考虑X–的符合相加修正,修正公式如下[2]:

2.3 峰总比测定
通过衰变纲图法计算多能核素的符合相加公式,大部分参数可以通过查表获得,全能峰效率参数可以通过测量相应的标准源获得,公式的难点是如何计算或测量各级联γ射线的总效率。如果要实验测得不同规格不同能量样品的总效率,不仅工作量巨大,而且结果还不尽满意。
Moens等[11]提出峰总比不变性的假设,认为全能峰效率与总效率的比值和源的位置、尺寸、介质组成等因素无关,是探测器的本征属性。樊元庆等[12]通过对单能核素制成的点源、面源和盘状源在不同位置对探测器峰总比进行了实验测量,也证实了高纯锗探测器的峰总比不变性。
γ谱仪峰总比/的公式定义如下:

在实际测量中,峰总比/也可以计数率的形式表示:

式中:p为全能峰计数率;t为谱总计数率;b为本底谱计数率;q为核素的其他γ射线峰计数率;0为外推至零点的计数率。
测量探测器峰总比的单能γ射线点源分别为241Am(59.5 keV)、109Cd(88.0 keV)、57Co(122.1 keV)、113Sn(391.7 keV)、137Cs(661.6 keV)、54Mn(834.8 keV)、65Zn(1 115.5 keV)。点源的生产厂家均为美国Eckert&Ziegler公司,规格为⌀25.4 mm×6.35 mm,由高强度塑料制成,源活性直径为5 mm。将点源分别放置在距离探测器表面5 cm、10 cm和15 cm的位置处(图1)进行峰总比测量,测量后对每个点源谱图都扣除了本底的影响,并且谱总计数率也外推至了零点。对三个位置处的峰总比刻度值取平均后,得到GC4019型高纯锗γ谱仪峰总比的刻度曲线(图2),并拟合成多项式方程如下:


图2 探测器峰总比对数图
3 结果与讨论
3.1 点源的符合相加修正
152Eu符合相加因子计算所需要的核素数据来自国际计量局(Bureau Internationaldes Poidset Measures,BIPM)机构编制的Monographie BIPM-5(Vol.2 A=151 to 242)数据库,152Eu核素的衰变主要分两部分:一部分通过轨道电子捕获方式(72.1%)和β+方式(0.027%)衰变到152Sm核素,另一部分通过β-方式(27.9%)衰变到152Gd核素。
152Eu核素的纲图比较复杂(图3),为了计算方便,不考虑发射概率在0.44%以下γ射线的级联符合干扰,简化后的152Eu核素各主要能量的符合相加修正公式如下:
121.8 keV(分支比为28.4%)的符合相加公式:

244.7 keV(分支比为7.6%)的符合相加公式:

344.3 keV(分支比为26.6%)的符合相加公式:

778.9 keV(分支比为13.0%)的符合相加公式:
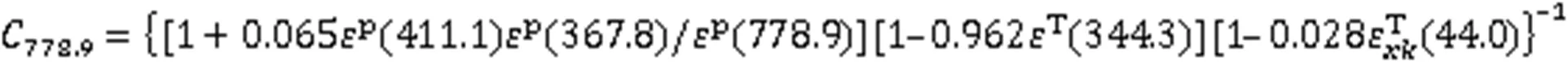
964.1 keV(分支比为14.5%)的符合相加公式:

1 112.1 keV(分支比为13.4%)和1 408.0 keV(分支比为20.8%)的符合相加公式如式(17)和(18):


刻度全能峰效率的单能核素点源与刻度峰总比所用点源一致,点源距离探测器表面距离为0 cm和5 cm时,分别刻度了点源的全能峰效率,效率公式如下。
0 cm位置处点源的全能峰效率公式:
ln()=–49.551+20.231 ln()–2.139 ln2()
<122 keV
ln()=–1.701+0.463 ln()–0.099 ln2()
≥122 keV (19)
5 cm位置处点源的全能峰效率公式:
ln()=–39.001+15.142 ln()–1.611 ln2()
<122 keV
ln()=–2.624+0.208 ln()–0.078 ln2()
≥122 keV (20)
根据符合相加修正公式,全能峰效率公式及峰总比拟合公式,可以求出152Eu点源距离探测器表面0 cm和5 cm的符合相加修正因子,符合相加修正结果如表1所示。

表1 点源符合相加修正结果和参考值的比较
两种距离下,152Eu点源不同能量的符合相加修正结果与参考值的相对偏差均不超过6%,说明用峰总比不变性与衰变纲图相结合的修正方法对点源进行符合相加修正是准确和可靠的,该方法不需要对不同位置的点源总效率进行测量,直接使用探测器的峰总比拟合公式和全能峰效率公式就可以求出不同能量的总效率,从而计算出符合相加修正因子。
3.2 点源符合相加修正的影响因素
点源符合相加效应与点源到探测器距离、探测器半径等参数有比较强的依赖关系,可以通过下式对两个光子级联符合相加的概率进行评估[13]:

式中:r为探测器半径;d为点源到探测器表面距离;d0为探测器晶体到探测器表面距离。

图5 点源到探测器距离与符合相加概率关系图(r=3.05 cm)
如图4所示,探测器半径越大,级联符合概率就会越高,符合相加效应也会越严重;而点源距探测器越远,符合相加概率就会越低,符合相加效应也越不显著,如图5所示,符合相加修正因子TCS与点源到探测器的距离平方2成反比关联关系,具体公式如下[14]:

C=1∙+2(23)
式中:C值可通过符合相加修正因子TCS求得,1、2为线性函数的参数,可通过同一能量下,任意两个距离及对应的C值拟合得到。对152Eu核素4个能量点(121.8 keV、244.7 keV、964.1 keV及1 408.0 keV),根据表1计算结果,拟合得到的线性公式如图6所示。
当符合相加修正因子小于1.01时,测量值和符合相加修正值的相对偏差小于1%,可以忽略符合相加效应对测量结果的影响。根据图6的拟合公式可以算出,源到探测器的距离>8.3 cm时,1 408 keV的符合相加效应可以忽略;>14.2 cm时,964.1 keV的符合相加效应可以忽略;>15.8 cm时,121.8 keV的能量可以忽略;>19.2 cm时,244.7 keV的符合相加效应可以忽略。

表2 液体体源符合相加修正结果和参考值的比较
3.3 液体源的符合相加修正
液体源的规格为⌀75 mm×70 mm,密度为1.05 g∙cm-3,测量几何条件为样品直接放置在探测器表面测量。对液体源分别通过衰变纲图数值计算法和Genie 2000蒙特卡罗程序法[15‒16]进行符合相加修正,蒙特卡罗程序使用的前提是需要对探测器进行工厂表征或使用和探测器尺寸相近的表征文件,以便获得谱仪的空间响应特性,然后通过Labsocs无源效率软件对实际测量的样品信息进行描述,在样品描述中介质类型选择水样(H2O),密度选择1.05 g∙cm-3,修正结果见表2。由结果可知,体源衰变纲图数值计算的偏差比蒙特卡罗程序计算的偏差大,特别是γ级联符合比较严重的能量244.7 keV,衰变纲图计算法的相对偏差为8.8%,而蒙特卡罗程序法相对偏差仅有-2.3%。蒙特卡罗程序符合相加修正时,将体源分割成大量的等体积的子源,然后计算出不同子源位置的全能峰效率和总效率,对子源加权平均后获得体源的符合相加修正因子。而直接用衰变纲图数值计算修正时,没有考虑不同能量的γ射线在体源内各点的效率不全相同,所以偏差较大。除121.8 keV、244.7 keV外,其余能量衰变纲图数值法计算的结果相对偏差均在5%以内。
蒙特卡罗程序使用时需要对待测样品的信息进行详细描述,在实际应用中待测样品并非全是水样,样品的介质组分大部分会比较复杂,如固体样、灰样等,在应急测量样品介质组成不确定时,舍去级联符合较严重的能量点(对152Eu核素,如244.7 keV、121.8 keV等),可以直接使用衰变纲图数值法对体源样品进行符合相加修正。
3.4 体源符合相加修正的影响因素

图7 点源及不同高度液体源的152Eu核素符合相加修正因子
图7为点源、⌀75 mm×5 mm液体源、⌀75 mm×35 mm液体源及⌀75 mm×70 mm液体源直接放置在探测器表面测量时,152Eu核素各主要能量点的符合相加修正因子。点源的修正方法为衰变纲图数值计算法,体源的修正方法为Genie 2000符合相加修正程序。由图5可知,在相同介质情况下,符合相加修正因子随着样品高度的增加而逐渐减小,即点源的修正因子最大,⌀75 mm×70 mm液体源的修正因子最小。其原因是:级联符合相加效应主要取决于样品和探测器的几何条件,一般探测立体角越大,符合相加效应越明显,随着样品高度的增加,立体角会逐渐变小,符合相加效应也会减弱。当体源的测量距离抬高到和§3.2中点源计算的符合相加效应可忽略的距离时,体源的符合相加效应也可以直接忽略。
图8为同样几何尺寸(⌀75 mm×70 mm,⌀75 mm×10 mm)下,水(H2O密度:1.0 g∙cm-3)、土壤(75%SiO2,15%Al2O3,10%Fe2O3;密度:1.6 g∙cm-3),二氧化硅(SiO2;密度:2.2 g∙cm-3),氧化铝(Al2O3;密度:3.7 g∙cm-3),氧化铁(Fe2O3;密度:5.2 g∙cm-3)5种介质在距离探测器表面0 cm的测量条件下,152Eu核素的符合相加修正因子。几何尺寸为⌀75 mm×70 mm(图8(a))时,氧化铁的符合相加修正因子在低能端(122 keV)明显高于其他低密度介质的修正因子,即密度越大,符合相加因子也越大;中能端(245 keV、344 keV),5种介质的符合修正因子差别不明显,最大相对偏差不超过5%;高能端(>779 keV)修正结果正好和低能端相反,即密度越小,符合相加修正因子越大。造成这种现象的原因是:低能端因为介质密度较高,进入探测器的低能γ射线主要以样品下半部分为主,导致样品的几何有效高度变小,相应的探测有效立体角也会变大。当几何尺寸为⌀75 mm×10 mm(图8(b))时,样品高度降低,低能γ射线都可以穿过整个样品,此时无论低能中能高能,都是高密度样品的符合相加修正因子低于低密度样品的修正因子,这是因为随着密度的增大,自吸收效应会逐渐减弱级联γ射线的符合相加效应。

图8 相同几何尺寸不同介质的152Eu核素符合相加修正因子(a) ⌀75 mm×70 mm,(b) ⌀75 mm×10 mm
4 结语
通过单能点源获得探测器的峰总比曲线,联合符合相加修正公式,全能峰效率公式,求出了多能核素点源的符合相加修正因子,计算结果与真值符合得较好,相对偏差在6%以内;点源的符合相加修正因子与点源到探测器的距离平方成反比,通过两个距离点建立线性拟合方程,从而获得点源符合相加效应可忽略的最小测量距离。探测器峰总比不变性和衰变纲图符合相加相结合的数值方法与蒙特卡罗程序法相比,无需对探测器进行工厂表征,不用对体源介质、密度和形状等参数进行描述,在舍弃级联符合较严重的能量点后,可直接用于环境应急样品的符合相加修正,并能得到较准确的修正结果。在P型探测器中,GC4019型探测器的能量分辨率和相对探测效率比较适中,在生态环境监测系统,大部分省级实验室都配备了该类型的探测器,在符合相加修正实验中选用该类型探测器具有一定的代表性和推广性。通过对不同高度样品的符合相加修正,验证了符合相加效应与样品高度成反比;同一位置处,相同体积不同介质样品的符合相加修正结果表明:高密度样品(⌀75 mm×70 mm)在低能端因为有效立体角变大,所以符合相加修正因子高于低密度样品的修正因子,样品在自吸收效应影响较小的高度时(⌀75 mm×10 mm),高密度样品的符合相加修正因子低于低密度样品的修正因子。
作者贡献声明 张磊:本研究的课题负责人,负责实验设计、数据整理和理论分析,本文撰写人。
1 Cheng H, Sun B H, Zhu L H,. Intrinsic background radiation of LaBr3(Ce) detector via coincidence measurements and simulations[J]. Nuclear Science and Techniques, 2020, 31(10): 99. DOI: 10.1007/s41365-020-00812-8.
2 谭金波. 锗γ能谱测量中的符合相加修正[J]. 辐射防护, 1989, 9(2): 101–109.
TAN Jinbo. Coincidence summing corrections in Ge γ-spectrometry[J]. Radialization Protection, 1989, 9(2): 101–109.
3 苏琼. γ谱分析中的γ-γ级联辐射的符合相加校正方法简介与评价[J]. 核技术, 2000, 23(10): 746–752.
SU Qiong. Simple introduction and evaluation about correction methods of coincidence summing effect of γ-γ cascade radiation in γ spectrometry[J]. Nuclear Techniques, 2000, 23(10): 746–752.
4 何宗慧, 黄治俭, 滕慧洁, 等. 近距离测量时Ge(Li)探测器的峰效率刻度符合相加修正[J]. 辐射防护, 1986, 6(6): 431–440, 453.
HE Zonghui, HUANG Zhijian, TENG Huijie,. Peak efficency calibration and coincident summing correction of a Ge(Li) detector at short source-to-detector distance[J]. Radialization Protection, 1986, 6(6): 431–440, 453.
5 Morel J, Chauvenet B, Kadachi A. Coincidence-summing corrections in gamma-ray spectrometry for normalized geometries[J]. The International Journal of Applied Radiation and Isotopes, 1983, 34(8): 1115–1122. DOI: 10.1016/0020-708X(83)90178-3.
6 Rizzo S, Tomarchio E. Numerical expressions for the computation of coincidence-summing correction factors in γ-ray spectrometry with HPGe detectors[J]. Applied Radiation and Isotopes, 2010, 68(4–5): 555–560. DOI: 10.1016/j.apradiso.2009.10.024.
7 Celik N, Altin D, Cevik U. Building-up a code for the purpose of TRUE coincidence summing correction in gamma-ray spectrometry with EGS4[J]. Radiation Physics and Chemistry, 2015, 115: 158–163. DOI: 10.1016/j.radphyschem.2015.07.002.
8 Giubrone G, Ortiz J, Gallardo S,. Calculation of coincidence summing correction factors for an HPGe detector using GEANT4[J]. Journal of Environmental Radioactivity, 2016, 158–159: 114–118. DOI: 10.1016/j.jenvrad.2016.04.008.
9 Rolle C, Lin Z C, Healey S. Computational approaches on photon-attenuation and coincidence-summing corrections for the detection of gamma-emitting radionuclides IN foods[J]. Applied Radiation and Isotopes, 2017, 126: 134–137. DOI: 10.1016/j.apradiso.2017.02.034.
10 李君利. 实验室γ能谱测量与分析[M]. 北京: 人民交通出版社, 2014.
LI Junli. Measurement and analysis of γ spectrum in laboratory[M]. Beijing: China Communications Press,2014.
11 Moens L, de Donder J, Lin X L,. Calculation of the absolute peak efficiency of gamma-ray detectors for different counting geometries[J]. Nuclear Instruments and Methods in Physics Research, 1981, 187(2–3): 451–472. DOI: 10.1016/0029-554X(81)90374-8.
12 樊元庆, 王军, 王世联. HPGe γ谱仪峰总比不变性的实验研究[J]. 原子能科学技术, 2006, 40(S1): 122–125. DOI: 10.3969/j.issn.1000-6931.2006.z1.028.FAN Yuanqing, WANG Jun, WANG Shilian. Experiment research on invariability of peak-to-total ratio in γ-ray spectrometry[J]. Atomic Energy Science and Technology, 2006, 40(S1): 122–125. DOI: 10.3969/j.issn.1000-6931.2006.z1.028.
13 Gilmore G R. Practical gamma-ray spectrometry[M]. Chichester, UK: John Wiley & Sons, Ltd, 2008. DOI: 10.1002/9780470861981.
14 Boshkova T. Experimental assessment of the coincidence summing corrections in gamma-ray spectrometry of bulk samples[J]. Applied Radiation and Isotopes, 2014, 83(Pt A): 1–7. DOI: 10.1016/j.apradiso.2013.10.009.
15 Genie 2000 spectroscopy software customization tools[M]. Canberra, 2006.
16 Zhu H, Morris K, Mueller W,. Validation of true coincidence summing correction in Genie 2000 V3.2[J]. Journal of Radioanalytical and Nuclear Chemistry, 2009, 282(1): 205–209. DOI: 10.1007/s10967-009-0148-x.
Coincidence summing correction methods and influence factors of γ spectrum
ZHANG Lei
()
In the radiation environmental quality measurement or emergency measurement, one of the factors that influence the measurement results of γ spectrum activity is the cascade coincidence summing effect of multienergy nuclides.This study aims to verify the accuracy of coincidence summing correction and analyze its influencing factors.152Eu nuclide was taken as an example object, the peak-to-total fitting formula of the detector was obtained according to the invariance characteristics of peak-to-total ratio. Combined with the coincidence summing correction formula and the full energy peak efficiency formula, and the coincidence summing correction factors of152Eu nuclide were calculated, and the Genie 2000 Monte Carlo program was used to correct152Eu nuclide of the bulk samples.The experimental results show that the relative deviation between the result and the true value is less than 6% of point source, and the relative deviation between the corrected results and the reference values is within ±4% of bulk samples. Through the linear relationship between the point source coincidence summing correction factor and the distance from the source to the detector, the minimum measurement distance with negligible coincidence summing effect can be obtained. The results of coincidence summing correction of bulk samples show that the higher the sample height is, the smaller the coincidence summing correction factor is.The numerical correction method combining peak-to-total ratio invariance and decay scheme, which does not require measurement of the point source total efficiency at different locations. Compared with the Monte Carlo program method, this method does not require factory characterization of the detector, nor does the parameters of the bulk sample such as medium, density and shape after abandoning the energies with serious cascade coincidence, hence be used for the coincidence summing corrections of the environmental emergency samples. In the low energy part, the self-absorption effect has a great influence on the effective solid angle of the sample, so that affecting the coincidence summing correction factor of the sample.
Coincidence summing correction, γ spectrum, Peak-to-total ratio
Supported by Youth Scientific Research Project of Shanghai Municipal Bureau of Ecology and Environment (No.2021-013)
ZHANG Lei, male, born in 1985, graduated from Fudan University with a doctoral degree in 2011, major in particle physics and nuclear physics, focusing on radiation monitoring and energy spectrum analysis
2022-03-17,
2022-04-21
TL817.2
10.11889/j.0253-3219.2022.hjs.45.060401
上海市生态环境局青年科研项目(No.2021-013)资助
张磊,男,1985年出生,2011年于复旦大学获博士学位,粒子物理与原子核物理专业,主要从事辐射监测和能谱分析研究
2022-03-17,
2022-04-21

