桨叶的组合共振理论建模与分析

李贞坤，程起有，朱艳，钱峰，刘晨，代志雄

（中国直升机设计研究所 直升机旋翼动力学重点实验室，江西 景德镇 333001）

旋转叶片广泛应用于工业领域，如风力发电机叶片、飞机发动机叶片、螺旋桨叶片以及直升机桨叶等。由于共振和颤动引起的桨叶失效问题是桨叶故障的主要原因之一，因此深入地了解旋转桨叶的动力学行为有助于减少桨叶的振动故障。

细长的桨叶可视为旋转的悬臂梁，基于线弹性小变形理论，研究者建立了诸多动力学模型来研究旋转梁的线弹性动力学行为，如旋转桨叶的共振频率与模态等问题。其后，研究者考虑了更复杂的情况，如旋转梁处于热环境、采用复合材料以及考虑裂纹等，以研究旋转梁的动特性。Qin等研究了旋转复合材料薄壁梁的自由振动特性，考虑了气动力和湿热环境的影响。Xie等采用有限元对含裂纹的旋转梁进行了研究，考虑了离心效应与裂纹效应的耦合。Liang等研究了弯扭耦合旋转梁，讨论了控制方程中螺旋项和离心项的作用。Guo等基于铁木辛柯梁理论，研究了含预安装角和扭转角的旋转渐变梁6个位移分量之间的耦合效应。

高速旋转的桨叶叶尖周围的流场非常不稳定，在强烈的周期性气流扰动下可能产生大振幅的非线性振动，而当前基于线弹性小变形理论获得的结果和结论不足以解释观测到的非线性问题。因此，研究者对旋转桨叶的非线性动力学行为（如主共振、次共振等）进行了研究，同时对功能梯度材料、温度分布、粘弹性等影响开展了讨论。Chen等研究了有预变形旋转梁的3∶1内共振，预变形来自热梯度分布，考虑了二次和三次非线性，采用多尺度法求解，并用数值法进行了验证。Thomas等考虑了不同非线性来源导致的几何非线性，分别建立了3种模型，采用解析和有限元的方法求解，研究了大挠度下的跳跃行为，以及不同转速下的软化/硬化特性。Emam等对附着有质量-弹簧系统的旋转梁亚结构的主共振进行了研究，采用摄动法求解，讨论了系统在自由振动和受迫振动下的响应。Yao等研究了变转速旋转梁的动特性，考虑梁的扭转和高温高速气流等的影响，采用数值方法分析了叶片的主共振及1∶1内共振。

在上述研究中，研究人员研究了旋转梁的主共振现象，即激励频率接近叶片的固有频率。非线性系统中存在更复杂的共振机制，其他不接近共振频率的激励频率也可能导致共振，如超谐波共振、亚谐波共振和组合谐波共振。以组合谐波共振为例，当桨叶受2个及以上频率激励时，如果2个激励频率满足特定的关系，即使2个频率均远离桨叶共振频率，桨叶同样会发生共振。Inoue等在实验中证实了风轮机叶片存在超谐波共振。Shahgholi等利用谐波平衡法研究了旋转轴的组合共振和次谐波共振。Zhang等探索了预扭转旋转梁的主共振、超谐波和组合谐波共振等情形，采用多尺度法求解，并使用Runge-Kutta法对结果进行了验证。熊春等采用多尺度法开展了旋转Rayleigh梁在轴向力下的参数稳定性分析，研究了超谐波共振和组合共振。伊海铭等针对双转子系统，采用四阶Runge-Kutta法分析了分岔区域的组合共振特性。

由以上文献总结可知，文献中对桨叶的非线性主共振研究较多，次共振特别是组合共振研究较少，而针对直升机桨叶的组合共振研究更少。本文对直升机桨叶的组合共振进行了研究，基于哈密顿原理推导出含几何非线性与非线性惯性的控制方程。采用伽辽金法离散，并使用摄动法中L-P法（Lindstedt-Poincaré method）求解，分析了组合共振发生条件及相应的稳态幅频响应，讨论了超/次谐波共振与组合共振共存的可能，并对组合共振进行了参数分析，探究了激励力和阻尼等对共振的影响。

1 建模与求解

1.1 模型建立与无量纲

如图1所示，以Bo105桨叶为研究对象，将桨叶视为旋转的细长悬臂梁，绕轴以角速度旋转，桨叶长度为，挥舞方向（方向）上受2个周 期变化分布的力、作用，激励力频率分别为、。桨叶轴向和横向位移分别为(,)、(,)，和分别表示横坐标和时间，、为作用力离固定端的距离。

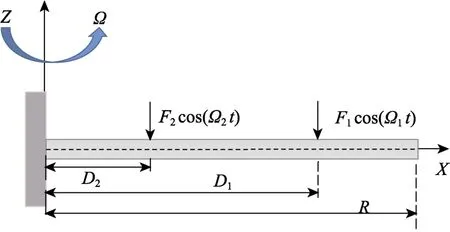
图1 桨叶受2个不同激励频率的力作用示意及坐标关系 Fig.1 Schematic diagram and coordinate relationship of the blades subjected to two different excitation frequencies

桨叶应变能可写为：

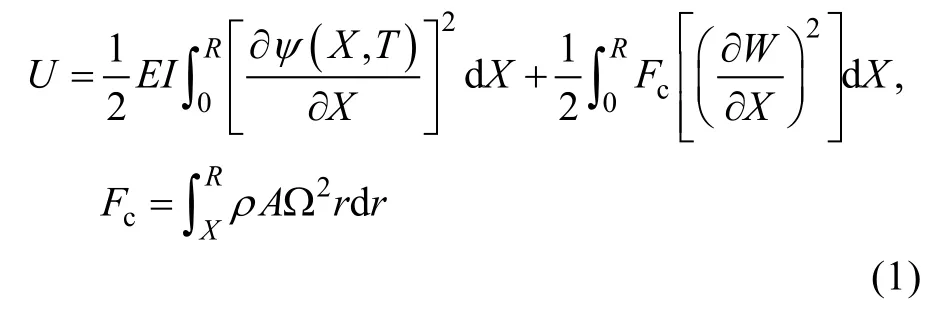
动能和外力功分别为：

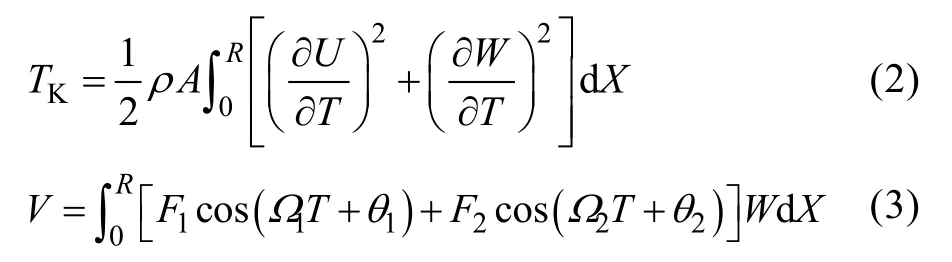
根据哈密尔顿原理，对总能量求变分：

将公式（1）—（3）代入方程（4）进行相应变换，并保留到三次项，可得旋转梁运动方程为：

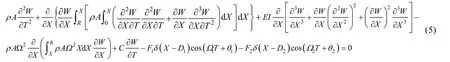
式中：为密度；为梁弯曲刚度，其中为弹性模量，为截面惯性矩；为阻尼系数；为Dirac函数。等式（5）左边与时间相关的三次项为非线性惯性，产生软化效应（Softening Effect），其他非线性项则为几何大变形引起，产生硬化效应（Hardening Effect），含项为旋转产生。如果令转速为0，方程退化成经典的悬臂梁非线性振动控制方程，见式（6）。

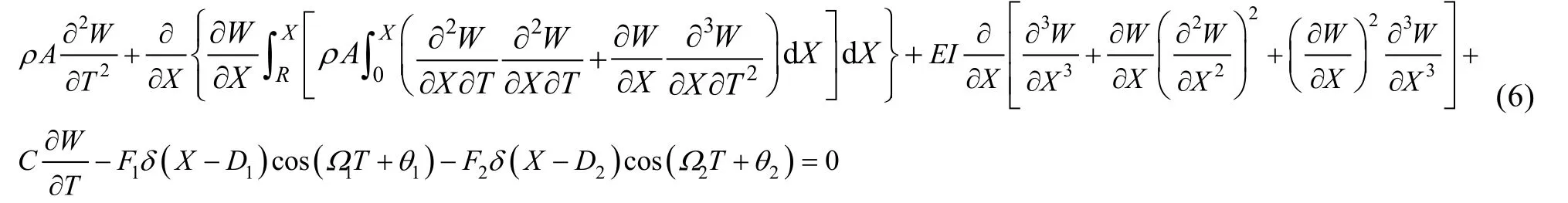
使用合适的参数，式（5）可无量纲化为：

采用的无量纲参数为：

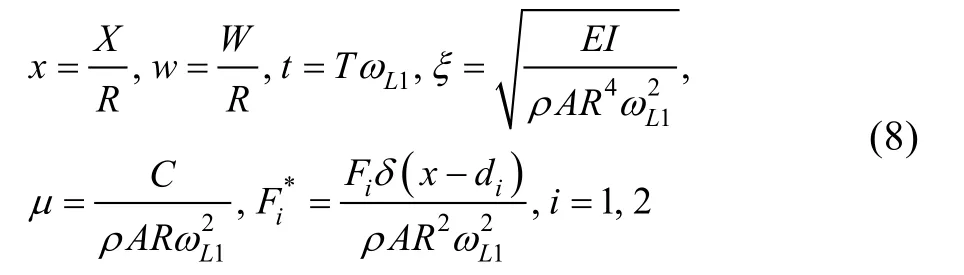
其中是悬臂梁一阶振动频率：

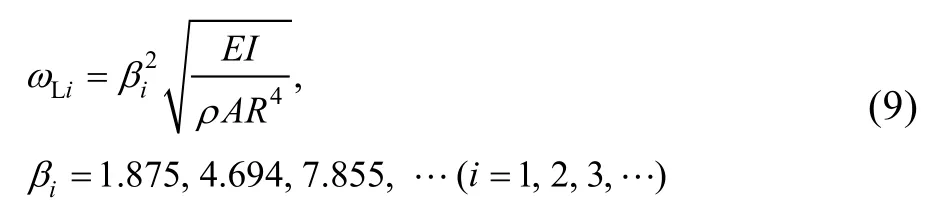
偏微分方程（7）可采用伽辽金法离散成二阶常微分方程：

式中：φ()为悬臂梁各阶模态函数；q()为对应的广义时间坐标。将式（10）代入式（7），并分别乘以对应的各阶模态函数φ()，对从0到1积分可得离散后的方程为（取=1）：

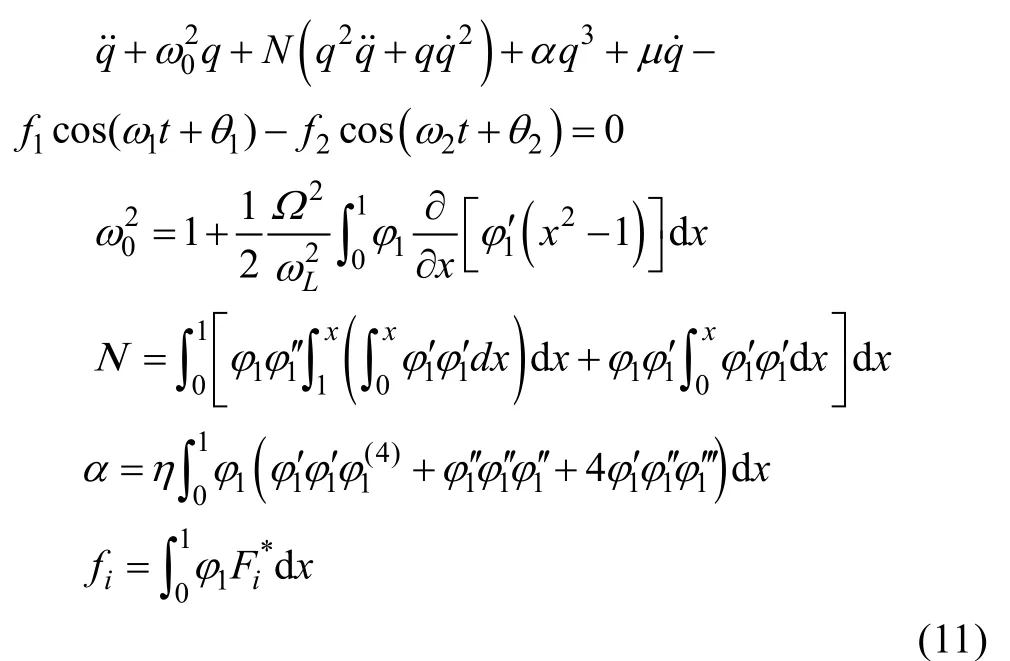
式中：上标点号(·)和撇号(')分别代表对时间和坐标的导数。

1.2 摄动法求解

在控制方程已离散的基础上，采用摄动法中的L-P法求解上述常微分方程。根据L-P法，式（11）可以写为：

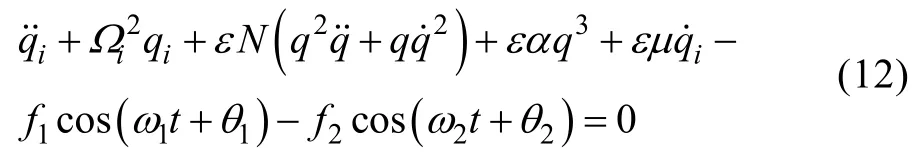
取新的时间变量=，并将激励频率ω和广义时间坐标q分别展开为的级数，见式（13）。

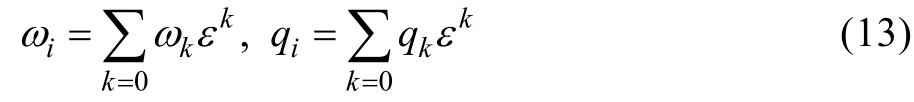
则关于时间的导数改写为：

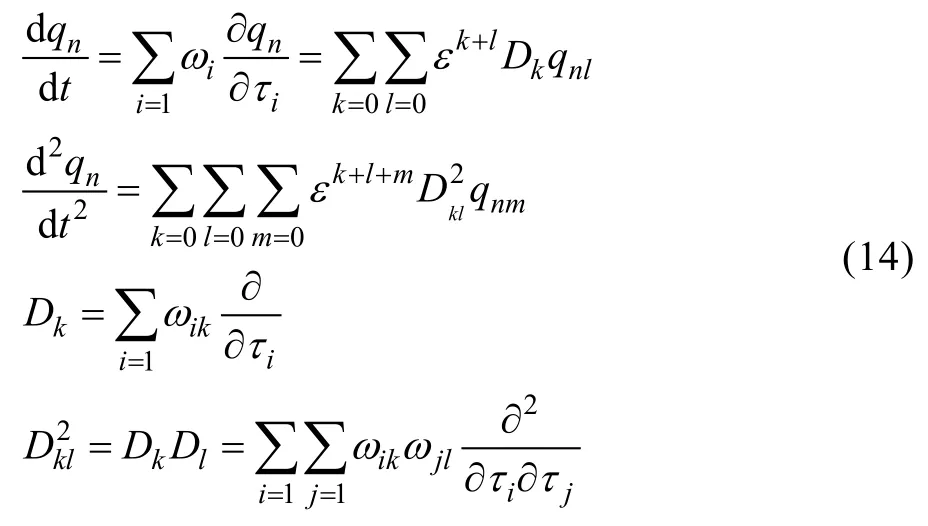
2个外激励频率改写为：

将式（13）—（15）代入方程（12），并令方程两端同次幂系数相等，得：

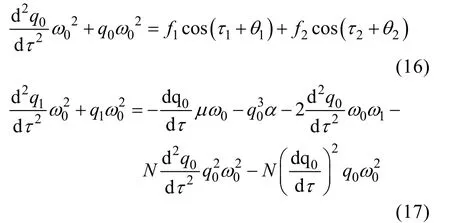
方程（16）的解为：

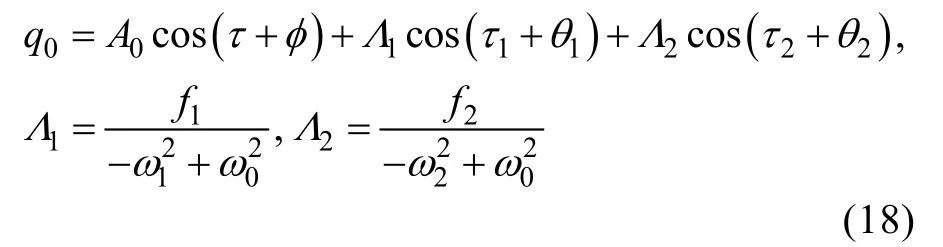
其中，解的第1项cos （+）表示自由振动，响应频率为旋转梁一阶共振频率，第2、3项表示受迫振动，响应频率与激励频率一致。

将方程的解（18）代入方程（17），提取同时含有,的项可得：

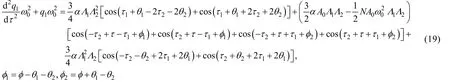
由式（19）可知，当,满足一定的关系，有可能发生组合共振，即：

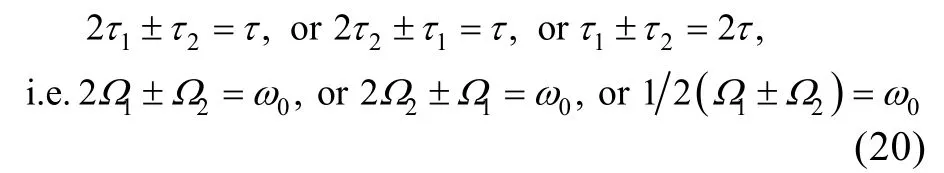
以2+=为例，此时2+=，为当前转速下悬臂梁共振频率，有：

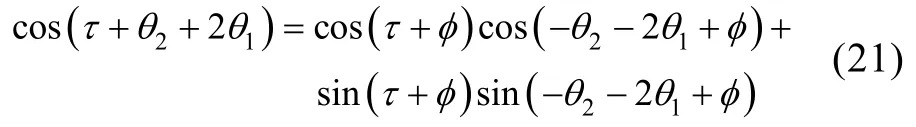
在式（19）中消除永久项，得幅频响应曲线为：

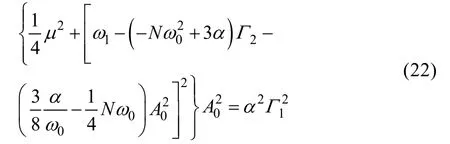
其中：

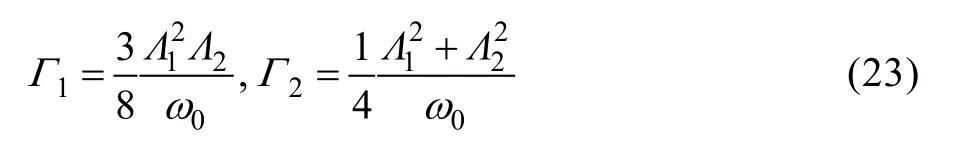
1.3 同时存在组合共振与超/次谐波共振

回到公式（19），只保留了同时包含和的项，其余的项被舍弃，以研究组合共振发生条件。在满足组合共振条件下，如果、还满足额外条件，则可能在组合共振产生的同时发生超谐波或次谐波共振。

将方程的解（18）代入方程（17），在所得的方程中提取包含或的项可得：

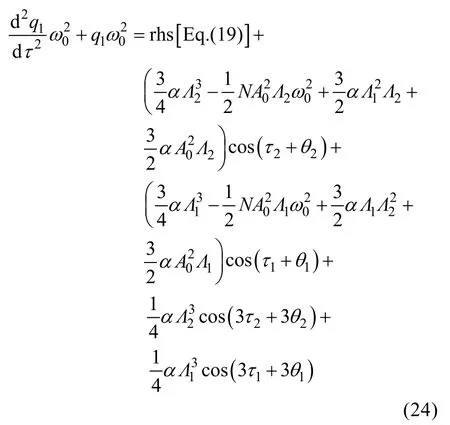
当满足式（20）任一条件时，会发生组合共振。若此时、还满足以下条件之一，则会同时发生超谐波共振：

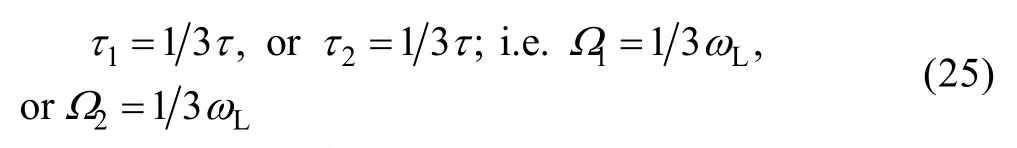
类似地，组合共振与次谐波共振会同时发生，若、还满足：

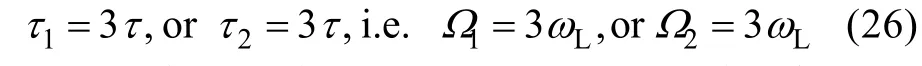
以同时存在组合共振与超谐波共振为例，使用公式（20）和式（25），即：

代入式（24）中消除永久项可得幅频响应方程为：

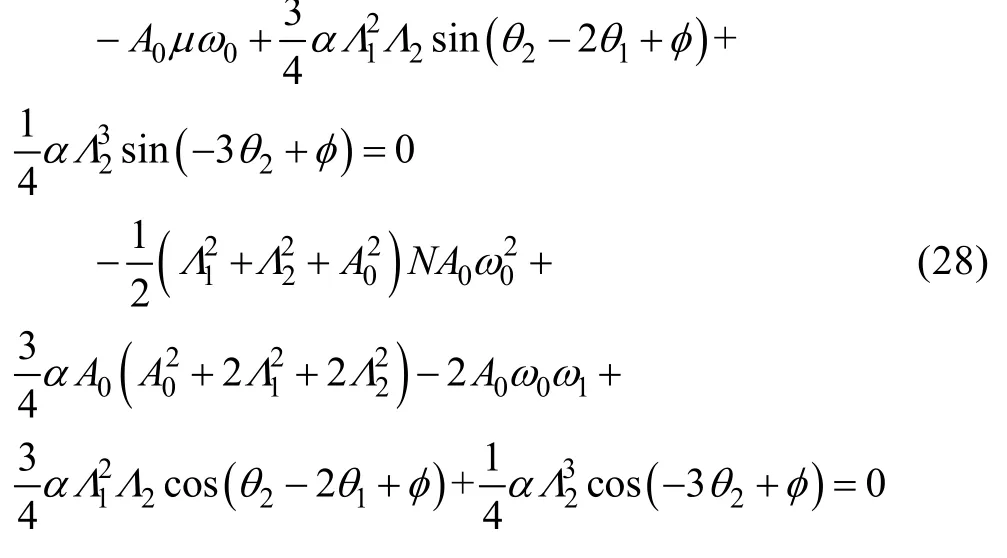
1.4 计算方法验证

为了验证本计算方法的有效性，采用L-P法对文献[24]中悬臂梁非线性振动控制方程进行求解，并与文献中结果进行比较。与文献一样采用一阶模态离散，离散后控制方程为：

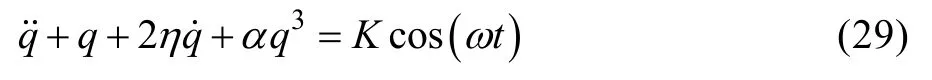
与1.3节类似，将激励频率ω和广义时间坐标q展开为的级数，并代入式（29），令方程两端同次幂系数相等得：

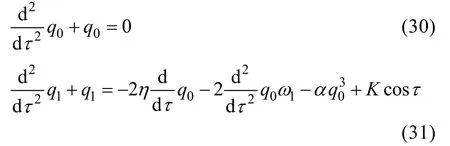
方程（30）的解为：=cos（+），代入方程（31）消除永久项可得幅频响应方程为：

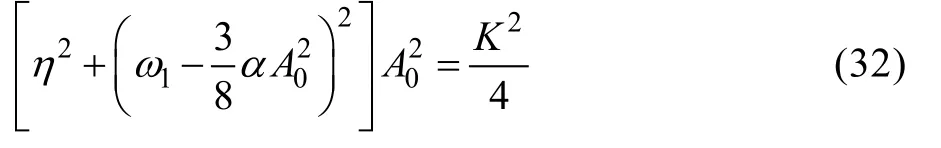
式（32）与文献中多尺度法结果一致，证明本文采用计算方法的正确性。

2 结果与讨论

2.1 组合共振

根据式（22）可作无量纲幅频响应曲线（如图2所示），采用的无量纲参数为：==0.05，=1.5×10。与线弹性振动相比，非线性振动幅频响应曲线与线弹性最显著的区别为在共振点附近曲线左右不对称。由图2可知，幅频响应曲线展现出向左偏的趋势，即表现出软化特性（Softening Effect），且幅频曲线的频率与振幅不再是一一对应，而是表现出多值性，以及跳跃现象。当激励频率由小增大，曲线沿着左下半支前行，在虚线处跳跃到右上半支；当激励频率由大减小，曲线沿着右半支前行，到顶点后跳跃到左下半支。

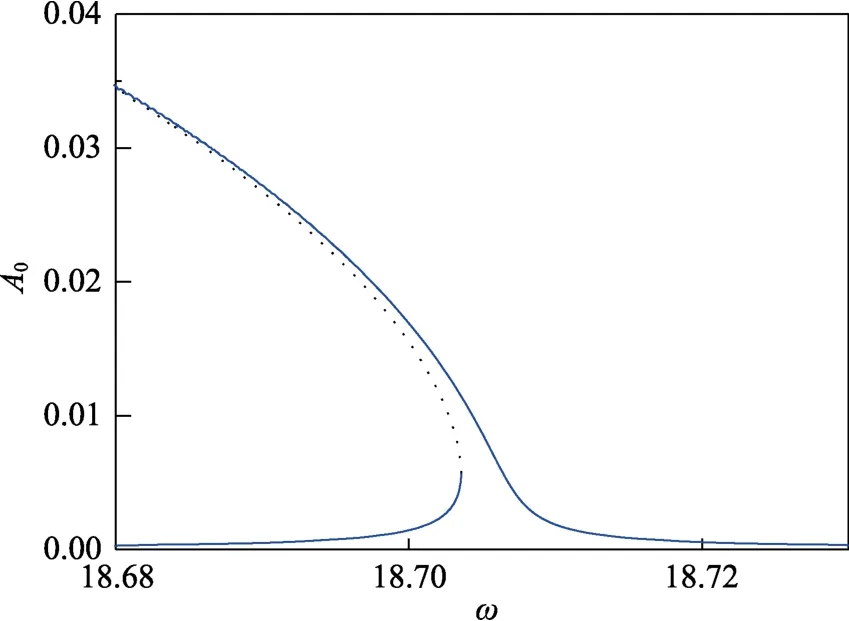
图2 无量纲幅频响应曲线 Fig.2 Dimensionless amplitude frequency resonance response curve

由式（18）可知，非线性振动与线弹性振动的另一区别在于桨叶的响应是由2部分组成：自由振动部分cos（+），频率为旋转悬臂梁共振频率；受迫振动部分cos（+）+cos （+），响应频率分别对应两激励力频率和，且发生组合共振时存在关系2+=，令：

取共振时桨叶的时间历程进行分析，如图3所示。图3a、b为受迫振动部分2个激励的响应，两者振幅相同，==0.05，相位不同。图3c为自由振动部分时间历程，无量纲振幅=0.11，大于两激励力振幅，且略大于两者的合振幅。图3d为旋转梁的合响应，振幅为三者的叠加，同时放上组合共振响应作对比，可以看出，组合共振振幅占总振幅的1/2。

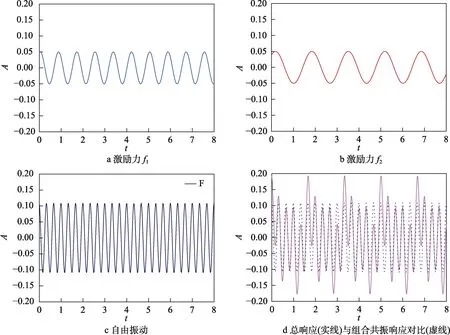
图3 无量纲时间历程 Fig.3 Dimensionless time histories at the resonance point: a) excitation force f1; b) excitation force f2; c) the free vibration part; d) the total response (solid line) and combined resonance response (dashed line)

2.2 参数分析

图4与图5分别展示了无量纲自由振动频响曲线和最大响应振幅随激励力、的变化。图4a和图5a表明，随着、增大，两无量纲响应振幅均增大，此为两者共同点。图4b和图5b表明，自由振动最大振幅随受迫激励力、增加的程度不一。图4b中，增大，振幅类似于幂指数增加；增大，振幅成比例增加。

图4 不同激励力f1下的无量纲频响曲线和最大振幅 Fig.4 Dimensionless frequency response curve (a) and the maximum amplitude (b) under different excitation force f1

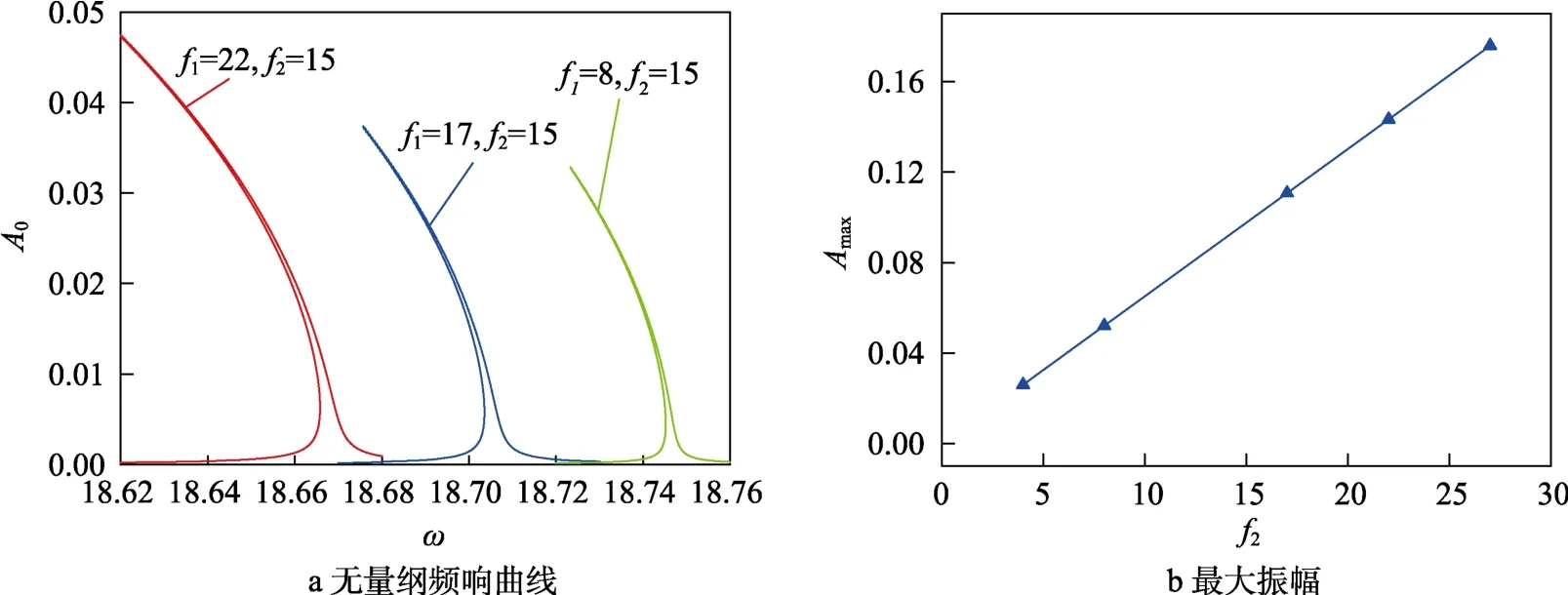
图5 不同激励力f2下的无量纲频响曲线和最大振幅 Fig.5 Dimensionless frequency response curve (a) and the maximum amplitude (b) under different excitation force f2

作最大振幅与激励力大小的比值图，如图6所示。可以看出，/呈线性关系，/为常数，表明组合共振振幅与激振力呈线性关系，却与呈平方关系，即在当前受力形势下（激励频率）对组合共振的振幅影响更大。

图6 Amax/ fi随fi变化（i=1,2） Fig.6 Ratio of Amax/ fi with different fi (i=1,2)

激励力位置对响应的作用如图7所示。无量纲参数和表示激励力、与固定端的距离。由图7 可知，随着的增加，即激励力远离固定端，曲线振幅相应增加；的影响趋势与一致。仔细对比图7a、b可知，响应的振幅随变化更剧烈。这与前文观察的现象一致，与相关联，响应振幅与成正比，而仅与成正比，因此响应随的变化更大。

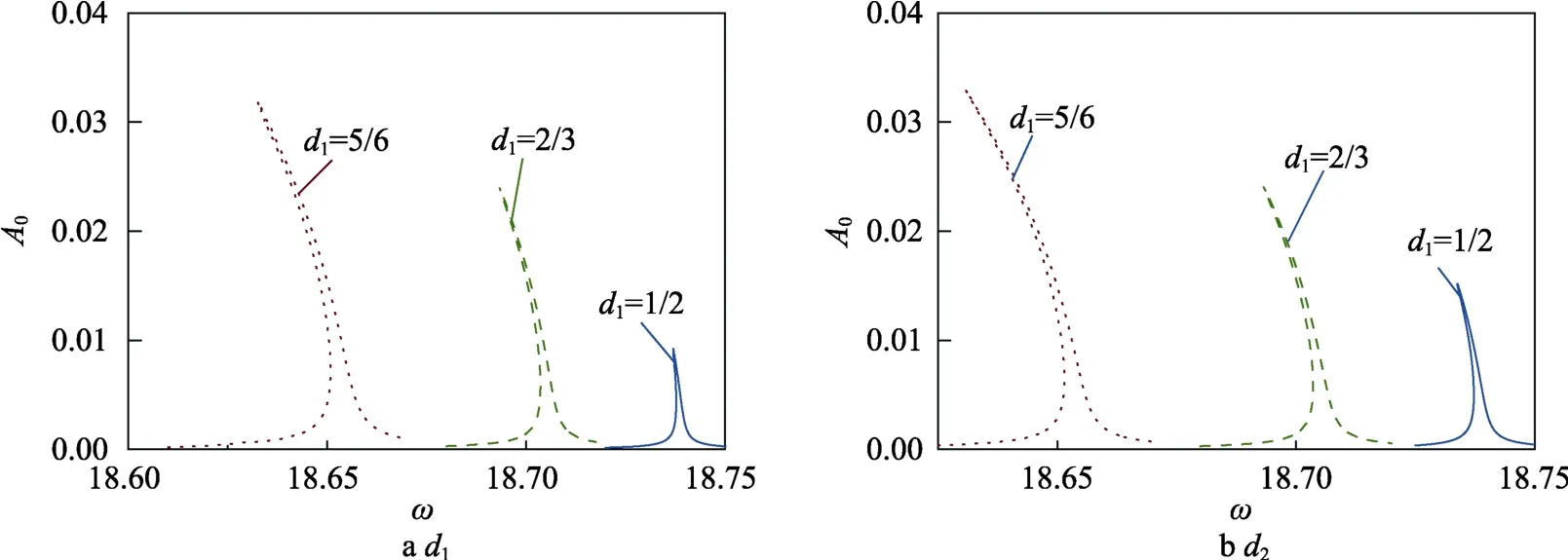
图7 响应随激励力位置的变化 Fig.7 Changes of position of the excitation force on the response

如前文所述，组合共振的存在极大地提高了旋转梁横向运动的振幅。对比图3c、d可知，组合共振使得振幅提高了1倍，极大地增加了桨叶的不稳定性和破坏的可能。不同阻尼下自由振动部分的无量纲频响曲线如图8所示。由图8b可知，增大阻尼能迅速地减小自由振动部分振幅，如无量纲阻尼从3×10增大到6×10，振幅降低了50%。因此，增大阻尼能有效抑制组合共振强度，防止旋转梁振幅过大而导致潜在的破坏。

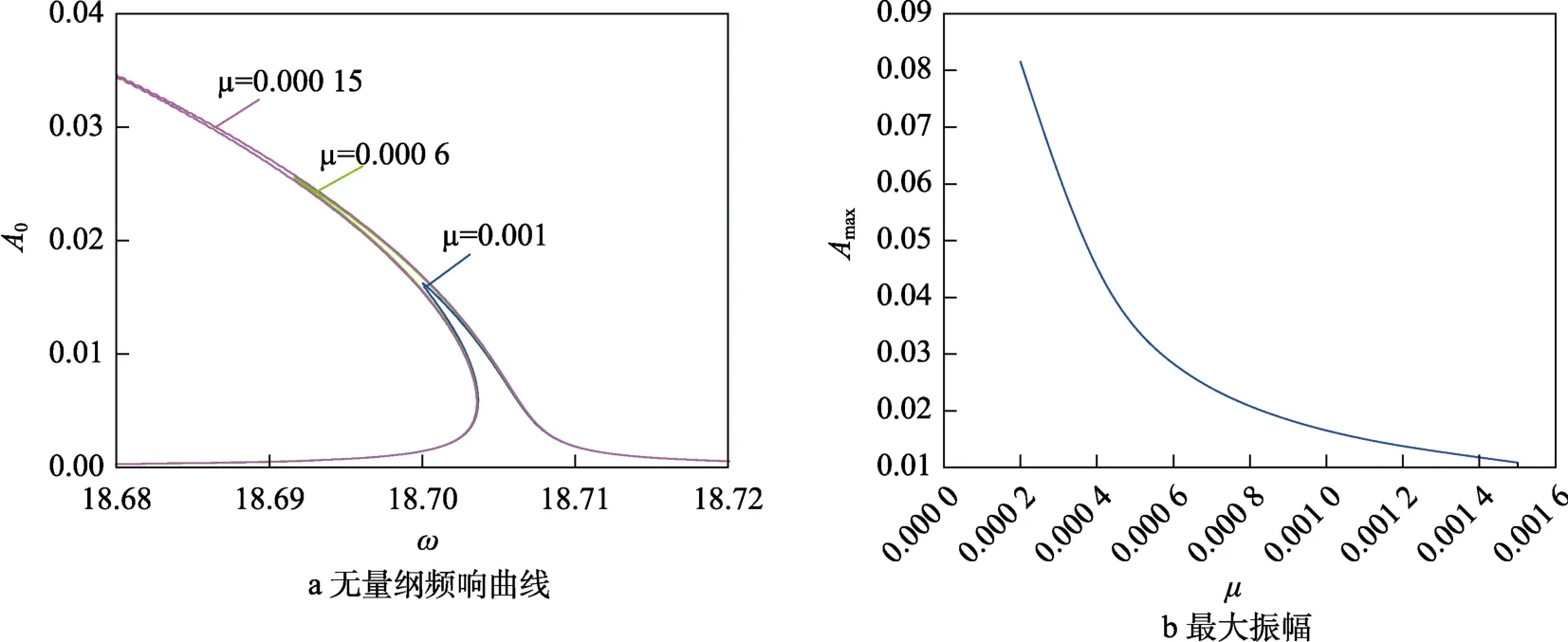
图8 不同阻尼下的无量纲频响曲线和最大振幅 Fig.8 Dimensionless frequency response curve (a) and maximum amplitude (b) under different damping;

2.3 超谐波共振与组合共振共存

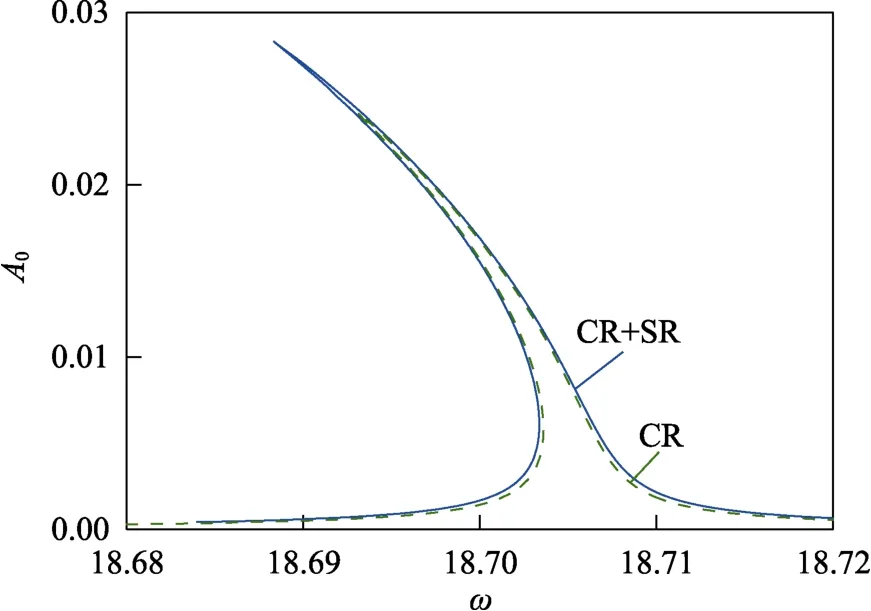
图9 有超谐波共振存在的组合共振（CR+SR）与 普通组合共振（CR）对比 Fig.9 Comparison of combination resonance (CR+SR) with the coexistence of super-harmonic resonance and commom combination resonance (CR)

3 结论

本文研究了旋转梁横向运动下受到2个激励力的组合共振，采用Hamilton原理推导了旋转梁控制方程，同时考虑了几何非线性与非线性惯性。采用L-P法对控制方程进行求解，获得了组合共振发生条件和共振时的幅频响应曲线方程，对组合方程进行参数分析，并进一步研究同时存在超/次谐波共振与组合共振的条件，研究获得如下结论：

1）当两激励频率满足2±=、2±=或1/2(±)=条件之一时，旋转梁可能发生组合共振，此时桨叶的响应既有2个激励频率成分，又有自由振动成分。

2）以2±=条件为例进行的分析表明，旋转梁表现出软化特性，组合共振中自由振动部分占主导，其振幅与两受迫振动振幅叠加相当。

3）参数分析表明，在2±=条件下，激振力的大小和位置对组合共振影响更大，振幅与呈平方关系，与呈线性关系。

4）在条件1）满足的情况下，若=1/3或=1/3，会同时存在超谐波共振；若=或=，会同时存在次谐波共振。=1/3的结果表明，同时存在超谐波共振时，会进一步增加组合共振的振幅。