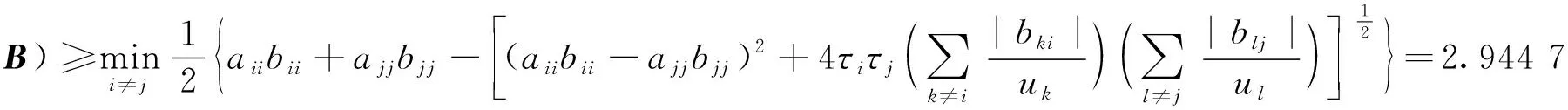矩阵Hadamard积与Fan积的特征值新界①

张晓凤， 陈付彬， 罗欢

昆明理工大学津桥学院 理工学院， 昆明 650106

矩阵在众多科学领域中有着极其广泛的应用， 是研究的重点[1-3]． 矩阵的Hadamard积与Fan积是两种与矩阵的乘法不同的运算[4]． 非负矩阵和M-矩阵相关特征值的研究是一个热点问题， 其中非负矩阵Hadamard积的谱半径上界和非奇异M-矩阵Fan积的特征值下界引起了学者们的关注， 且相继给出了许多结果[5-19]． 下面将继续针对这两个问题进行研究， 得到只依赖相关矩阵元素且更具优越性的结果．

1 预备知识

以Rn×n(Cn×n)表示实(复)矩阵集，N表示集合{1， 2， …，n}．

如果矩阵A=(aij)的元素满足aij>0(i，j∈N)， 则A是正矩阵， 记A>0； 如果满足aij≥0(i，j∈N)， 则A是非负矩阵， 记A≥0．

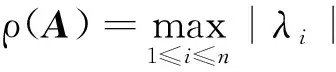
设A=(aij)，B=(bij)∈Rn×n． 用A∘B表示A和B的对应元素相乘的矩阵， 称为A和B的Hadamard积， 如果A≥0，B≥0， 则A∘B≥0．

如果有置换矩阵P， 使得

则称A可约， 否则A不可约．

记

Zn={A=(aij)：aij≤0(i≠j)；i，j=1，…，n}

设A=αI-P，P≥0，α∈R， 若α>ρ(P)， 则A为非奇异M-矩阵， 记为Mn； 否则A是奇异的．

设A=(aij)，B=(bij)∈Rn×n，A★B=(cij)定义为A与B的Fan积， 其中

如果A，B∈Mn， 则A★B∈Mn．

本文将用到以下记号： 令A=(aij)，i，j，k∈N，j≠i，

2 非负矩阵Hadamard积的谱半径上界

引理1[18]设A=(aij)∈Cn×n， 则A的特征值位于如下域中：

引理2[18]设A=(aij)∈Cn×n， 则A的特征值位于如下域中：

定理1设A=(aij)，B=(bij)∈Rn×n， 且A，B≥0， 则

证当n=1时， 结论明显成立． 当n≥2时， 分以下两种情况讨论：

情况1 若A∘B不可约． 则A和B也不可约． 依据引理1， 当i∈N时， 有

由于ρ(A∘B)≥aiibii， 则

情况2 若A∘B可约． 则有满足ξ12=ξ23=…=ξn-1，n=ξn，1=1， 且其余元素ξij=0的置换阵D=(ξij)， 当正数ε充分小时，A+εD和B+εD非负不可约． 将A，B替换为A+εD，B+εD， 同情况1的讨论， 结论成立．

定理2设A=(aij)，B=(bij)∈Rn×n， 且A，B≥0， 则

证当n=1时， 结论明显成立． 当n≥2时， 分以下两种情况讨论：

情况1 若A∘B不可约． 则A和B也不可约． 令ρ(A∘B)=λ， 依据引理2， 存在(i，j)， 1≤i，j≤n，i≠j， 有

由于ρ(A∘B)≥aiibii， 则

情况2 若A∘B可约． 则有满足ξ12=ξ23=…=ξn-1，n=ξn，1=1， 且其余元素ξij=0的置换阵D=(ξij)， 当正数ε充分小时，A+εD和B+εD非负不可约． 将A，B替换为A+εD，B+εD， 同情况1的讨论， 结论成立．

下面比较定理1和定理2的优越性． 不失一般性， 当i≠j时， 假设有

即

则

因此

所以

例1令非负矩阵

应用文献[8-15]中ρ(A∘B)的相关定理分别得

ρ(A∘B)≤50.127 4ρ(A∘B)≤25.536 4ρ(A∘B)≤31.461 1ρ(A∘B)≤23.200 0

ρ(A∘B)≤28.446 0ρ(A∘B)≤25.364 4ρ(A∘B)≤22.163 3ρ(A∘B)≤21.887 2

而应用所给定理1， 得

应用定理2， 得

3 非奇异M-矩阵Fan积的特征值下界

定理3设A=(aij)，B=(bij)∈Mn， 则

证当n=1时， 结论明显成立． 当n≥2时， 分以下两种情况讨论：

情况1 若A★B不可约． 则A和B也不可约． 依据引理1， 当i∈N时， 有

由于0≤τ(A★B)≤aiibii， 则

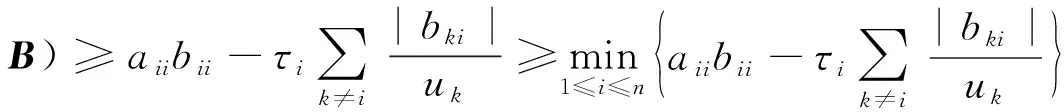
情况2 若A★B可约． 因为Zn中的矩阵满足主子式皆为正时为M-矩阵[19]， 则有满足ξ12=ξ23=…=ξn-1，n=ξn，1=1， 且其余元素ξij=0的置换阵D=(ξij)， 当正数ε充分小时，A-εD和B-εD为M-矩阵且不可约． 将A，B替换为A-εD，B-εD， 同情况1的讨论， 结论成立．

定理4设A=(aij)，B=(bij)∈Mn， 则

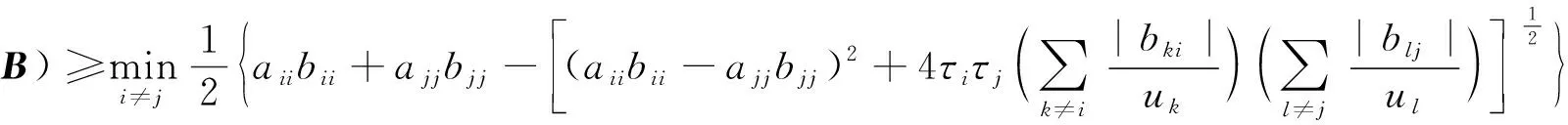
证当n=1时， 结论明显成立． 当n≥2时， 分以下两种情况讨论：

情况1 若A★B不可约． 则A和B也不可约． 令τ(A★B)=λ， 依据引理2， 存在(i，j)， 1≤i，j≤n，i≠j， 有

由于0≤τ(A★B)≤aiibii， 则

情况2 若A★B可约． 因为Zn中的矩阵满足主子式皆为正时为M-矩阵[19]， 则有满足ξ12=ξ23=…=ξn-1，n=ξn，1=1， 且其余元素ξij=0的置换阵D=(ξij)， 当正数ε充分小时，A-εD和B-εD为M-矩阵且不可约． 将A，B替换为A-εD，B-εD， 同情况1的讨论， 结论成立．

下面比较定理3和定理4的优越性． 不失一般性， 当i≠j时， 假设有

即

则

因此

所以

例2令M-矩阵

应用文献[8-14， 16]中τ(A★B)的相关定理分别得

τ(A★B)≥0.191 0τ(A★B)≥1.573 0τ(A★B)≥1.523 8τ(A★B)≥2.433 3

τ(A★B)≥1.573 0τ(A★B)≥1.523 8τ(A★B)≥2.833 3τ(A★B)≥2.921 2

而应用本文定理3得

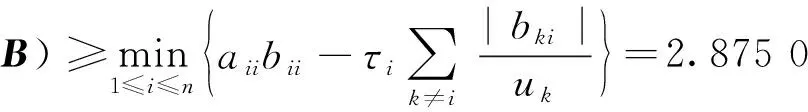
应用定理4得