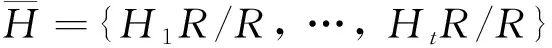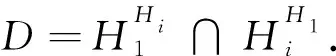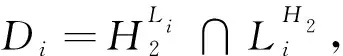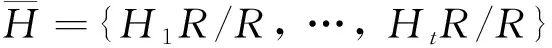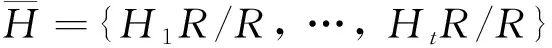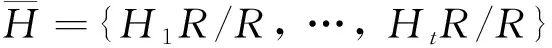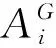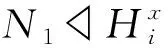有限群的σ半次正规子群①
郑毅, 吴珍凤, 殷霞, 杨南迎
江南大学 理学院, 江苏 无锡 214122
文中所涉及的群均为有限群.G总表示一个有限群, |G|表示G的阶,π(n)表示所有整除n的素因子的集合, 且π(G)=π(|G|). |G|π表示能整除|G|且素因子均在π中的最大整数.
文献[1]首次引入了半正规的概念: 假定H≤G, 如果G中存在子群K, 满足G=HK, 且对任一K1 文献[2]利用子群的半正规性, 推广了Ito定理. 文献[3]结合次正规和半正规的概念引入了半次正规的概念: 假定A≤G, 如果A在G中次正规或者半正规, 则称A在G中是半次正规的, 并得到了有限群超可解的若干判别准则. 近些年, 学者们通过利用有限群的σ-理论和半正规子群的性质来研究有限群, 得到了有限群结构的许多重要的结果(参见文献[3-12]). 通过分析这些已有的结果与方法, 本文结合σ-次正规性和半正规性引入了如下概念: 定义1假定A≤G, 如果A在G中σ-次正规或者半正规, 则称A在G中是σ-半次正规的. 由定义, 半次正规子群显然也是σ-半次正规子群, 但下面的例子表明反之不成立: 例1设G=PSL2(7), 则|G|=23·3·7, 且G中含有一个阶为3·7的极大子群, 记为M. 令σ={σ1,σ2}, 其中σ1={2, 3, 7},σ2={2, 3, 7}′. 则G是σ-幂零的, 从而由文献[3]的命题2.3知M在G中是σ-次正规的, 则M是σ-半次正规的. 若M在G中是半次正规的, 那么由于G是单群, 故M在G中是半正规的, 从而存在B≤G使得G=MB, 且对任意B1 通过研究σ-半次正规子群, 我们给出有限群的σ-可解性和超可解性的一些新的充分条件. 未交代的符号和概念参见文献[13-19]. 引理1[4,6]设A,K和N是群G的子群. 假设A在G中是σ-次正规的, 并且N正规于G, 则: (i)A∩K在K中是σ-次正规的; (ii)AN/N在G/N中是σ-次正规的; (iii) 若A是G的σ-Hall子群, 则A正规于G; (iv) 若H≠1是G的HallΠ-子群, 且A不是Π′-群, 则A∩H≠1且是A的HallΠ-子群; (v) 若G是Π-完全群, 且A是Π-群, 则A≤OΠ(G). 引理2[15]设G是群,H≤X≤G且N正规于G, 则下列结论成立: (i) 如果H在G中半正规, 则H在X中半正规; (ii) 如果H在G中半正规, 则HN/N在G/N中半正规; (iii) 如果H在G中半正规, 且K是H在G中的S-补, 则对∀g∈G和L≤K,H与Lg置换, 特别地, 对任意g∈G,Kg是H在G中的S-补. 引理3设G是群,H≤X≤G, 如果H在G中σ-半次正规, 则下列结论成立: (i)H在X中σ-半次正规; (ii) 若N正规于G, 则HN/N在G/N中σ-半次正规. 证如果H在G中σ-次正规, 则由引理1得(i)-(ii)成立; 如果H在G中半正规, 则由引理2得(i)-(ii)成立. 因此(i)-(ii)成立. 引理4[4]σ-可解群在子群、 同态像和直积下是封闭的. 并且任意两个σ-可解群的扩张还是σ-可解群. 引理5[5]令H是群G的次正规且σ-可解子群, 那么H≤Rσ(G). 引理6[15]令H是群G的半正规Hallπ-子群, 那么H在G中的任一S-补都是G的Hallπ′-子群. 引理7[15]令H是群G的半正规子群, 且K是H在G中的S-补, 那么对K的任一子群L,HL∩LH在G中次正规. 引理8[16]若X是群G的次正规且π-可解子群, 则XG是π-可解群. 引理9[17]设G是群,P∈Sylp(G)且P循环. 若p是整除|G|的最小素因子, 则G有正规p-补, 即G为p-幂零群. 引理10[18]有限群G是超可解群当且仅当G的所有极大子群的指数是素数. 定理1设群G是具有Sylow型的σ-完全群, 且有完全Hallσ-集H={H1, …,Ht}. 令p是整除|G|的最小素因子, 假设对任意的i=1,…,t,Hi是p-幂零群. 如果对所有的非循环子群Hi,Hi在G中都是σ-半次正规的, 那么G是σ-可解群. 证假设结论不成立, 并设群G是一极小阶反例, 我们分以下步骤来证明: 步骤1如果R是群G的一个极小正规子群, 那么G/R满足定理1的假设, 从而G/R是σ-可解的. 步骤2Rσ(G)=1. 假设Rσ(G)≠1, 则G存在非平凡的σ-可解正规子群N. 那么由步骤1知,G/N是σ-可解的, 从而由引理4知G是σ-可解的, 矛盾. 因此Rσ(G)=1. 步骤3对任意非循环的子群Hi, 都有Hi半正规于G. 由假设, 对任意非循环的子群Hi, 都有Hi在G中σ-次正规或半正规. 如果Hi在G中σ-次正规, 则由引理1(iii)可知Hi正规于G, 与步骤2矛盾. 这表明对任意非循环的子群Hi, 都有Hi半正规于G. 步骤4令p∈σ1. 则H1是非循环的且在G中半正规. 若H1是循环的, 则G的Sylowp-子群也是循环的, 从而由引理9知G是p-幂零的. 又因为p是整除|G|的最小素因子, 所以G是可解的, 矛盾, 故H1是非循环的. 因此由步骤3知,H1在G中是半正规的. 步骤5|σ(G)|=2且G=H1H2. 由步骤4知H1半正规于G. 根据引理6得,G存在Hallσ′1-子群K, 使得K是H1在G中的S-补. 令L是K的任一Hallσi-子群(i≠1), 则L也是G的Hallσi-子群. 又因G是具有Sylow型的σ-完全群, 从而存在x∈G使得Lx=Hi. 于是由引理2(iii)可得H1Hi≤G, 并且Kx也同样是H1在G中的S-补. 因此由引理3(i)得H1Hi满足定理假设. 如果|σ(G)|>2, 那么H1Hi 我们得到D是σ-可解的. 再根据引理5, 我们有D≤Rσ(G). 故由步骤2, 得到D=1, 从而 因此Hi≤CG(H1). 由Hi选取的任意性知H1◁G, 但这与步骤2矛盾. 因此|σ(G)|=2, 即G=H1H2. 步骤6最后矛盾. 下面分两种情况讨论: 情况1H2非循环. 由步骤3知H1,H2在G中半正规, 再由引理6和引理2(iii)可得,H1是H2在G中的S-补, 同时H2也是H1在G中的S-补. 现设L1,L2是H1的两个不同的极大子群, 且Ai=H2Li,i=1,2, 则 A1=H2L1 我们断言A1,A2均是σ-可解的. 显然{Li,H2}是Ai的完全Hallσ-集,Li=H1∩Ai是Ai的Hallσ1-子群. 因为H2是H1在G中的S-补, 所以对任意B H1B∩Ai=(H1∩Ai)B=LiB 所以Li≤CG(H2). 又因为H1=〈L1,L2〉, 从而H1≤CG(H2), 故H2◁G, 矛盾. 情况2H2循环. 由步骤4知H1在G中半正规, 从而由引理6知H2是H1在G中的S-补. 我们断言|H2|=q. 设Q是H2的一个极大子群, 则H1Q是G的真子群. 因{H1,Q}是H1Q的完全Hallσ-集, 且由引理3得H1Q满足定理假设, 所以由G的选取知H1Q是σ-可解的. 于是同情况1同样的讨论可得到H1≤CG(Q), 故Q◁G. 由步骤2,Q=1, 从而|H2|=q, 故G是可解群, 矛盾. 综上所述, 定理1得证. 推论1[15]如果群G的所有非循环Sylow子群在G中半正规, 那么G是可解群. 定理2设群G有完全Hallσ-集H={H1, …,Ht}, 使得Hi均为超可解子群, 对于所有i=1,…,t, 如果G的任意极大子群在G中都是σ-半次正规的, 那么G是超可解群. 证假设定理2不成立, 并设群G是一极小阶反例, 我们分以下步骤来证明: 步骤1若R是群G的一个非平凡的极小正规子群, 则G/R是超可解群. 步骤2G有唯一极小正规子群, 记作R. 设R1和R2是G的两个不同极小正规子群, 则由步骤1知,G/R1和G/R2均为超可解的, 故G是超可解群, 矛盾. 步骤3最后矛盾. 设M是G的任一极大子群. 如果R≤M, 那么M/R是G/R的极大子群, 于是由步骤1知,G/R是超可解群. 所以根据引理10, 我们有|G∶M|=|G/R∶M/R|为素数. 如果R≤/M, 那么G=RM, 且由假设,M在G中σ-半次正规. 若M在G中σ-次正规, 则M◁G或者G/MG为σ-准素的. 若M◁G, 则由R的唯一性知M=1, 从而G是素数阶循环群, 矛盾. 若G/MG为σ-准素的, 则对某个Hi∈H,G/MG=HiMG/MG, 因Hi是超可解的, 从而G/MG为超可解群, 故MG≠1. 又由步骤2知,R≤MG≤M, 矛盾. 该矛盾表明M在G中半正规. 现设K是M在G中的S-补, 则G=MK, 且对任意H MK1∩K=(M∩K)K1=K 从而可得 MK1=M(M∩K)K1=MK=G 矛盾, 故M∩K≤Φ(K). 设L是K的任一极大子群, 则ML是G的真子群. 又因M是G的极大子群, 于是ML=M, 则L≤M∩K≤K, 因此L=M∩K. 从而 Φ(K)≤L=M∩K≤Φ(K) 于是L=M∩K=Φ(K)是K的极大子群, 这表明K的极大子群唯一, 从而K为素数幂阶循环群, 故|G∶M|=|K∶M∩K|为素数. 因此, 对G的任一极大子群M, 都有|G∶M|为素数. 由引理10可知,G是超可解群, 矛盾. 定理2得证. 推论2[3]如果群G的所有极大子群在G中半正规, 那么G是超可解群. 定理3设群G是具有Sylow型的σ-完全群, 且有完全Hallσ-集H={H1, …,Ht}. 令p是整除|G|的最小素因子, 且当p∈σi时,Hi是超可解群. 如果Hi的所有极大子群都在G中σ-半次正规, 那么G是σ-可解群. 证假设定理3不成立, 并设G是一极小阶反例, 则由Feit-Thompson定理可知p=2. 不失一般性, 可假设p∈σ1. 步骤1如果R是G的非平凡正规子群, 那么G/R是σ-可解群. 若2⫮|H1R/R|, 则G/R为2′-群, 从而G/R是可解群. M=M∩H1R=(M∩H1)R 因为H1是超可解群, 所以由引理10知|H1R/R∶M/R|=|H1R∶M|=|H1∶M∩H1|是素数, 从而M∩H1是H1的极大子群. 则由引理3知(M∩H1)R/R=M/R在G/R中σ-半次正规, 故G/R满足定理假设. 因此由G的选取可知,G/R是σ-可解群. 步骤2Oσ1(G)=Oσ′1(G)=1. 若Oσ1(G)≠1, 则由步骤1知G/Oσ1(G)为σ-可解群. 又因Oσ1(G)是σ-可解的, 从而根据引理4得到G是σ-可解的, 矛盾, 故Oσ1(G)=1. 若Oσ′1(G)≠1, 则由步骤1知G/Oσ′1(G)为σ-可解群. 又因Oσ′1(G)为奇数阶的, 故是可解群, 从而根据引理4得到G是σ-可解的, 矛盾, 因此Oσ′1(G)=1. 步骤3最后矛盾. 因此|H1|=2, 从而由引理9知G是可解群, 矛盾. 因此M在G中半正规. 设K是M在G中的S-补, 则G=MK. 于是对任意q∈σi∩π(G)(i=2,…,t), 有q||K|. 设Q∈Sylq(K), 令D=MQ∩QM, 则由引理7知D次正规于G. 如果D=1, 那么 [M,Q]≤[MQ,QM]≤MQ∩QM=1 从而Q≤CG(M). 则由q的任意性知|G∶NG(M)|是σ1-数, 又由M◁H1可得M◁G, 与步骤2矛盾. 因此存在Q∈Sylq(K), 使得D=MQ∩QM≠1. 显然D≤MQ, 于是由引理3知M在MQ中半正规. 又因为M≤H1是超可解的, 则M为2-幂零的, 从而由文献[15]的定理1知MQ为π(M)-可解的, 进而由引理8知DG为π(M)-可解的. 令R是G的极小正规子群, 且R≤DG, 则R亦是π(M)-可解的. 再因|H1∶M|=2, 那么π(H1)=π(M)或者π(H1)=π(M)∪{2}. 如果π(H1)=π(M), 则R为π(H1)-可解的, 从而R是π′(H1)-群或初等交换t-群, 其中t∈σ1. 若R为π′(H1)-群, 则R≤Oσ′1(G)=1, 矛盾. 若R是初等交换群, 则R≤Oσ1(G)=1, 矛盾. 如果π(H1)=π(M)∪{2}, 那么|H1|2=2, 从而由引理9知G是可解群. 综上所述, 定理3得证. 定理4设群G是具有Sylow型的σ-完全群, 且H={H1, …,Ht}是G的一个完全Hallσ-集, 使得对所有的i=1,…,t,Hi是超可解群. 令A和B是G的子群, 且G=AB. 如果A,B的所有Hallσi-子群在G中都是σ-半次正规的, 那么G是超可解群. 证不失一般性, 可设Hi是G的Hallσi-子群(i=1,…,t). 假设定理4不成立, 并设群G是一极小阶反例, 我们分以下步骤来证明: 步骤1对G的任一非平凡的正规子群R,G/R是超可解群. 令R是G的任一非平凡的正规子群, 则 G/R=AR/R·BR/R H=(H∩A)R 且 |AR/R∶H/R|=|AR∶H|=|AR∶(H∩A)R|=|A∶H∩A| 是σ′i-数. 再令S是H∩A的任一Hallσi-子群, 则|A∶S|=|A∶H∩A||H∩A∶S|是σ′i-数. 从而S是A的一个Hallσi-子群, 则由假设知S在G中是σ-半次正规的. 又因为 SR/R≤H/R 且 |AR/R∶SR/R|=|AR∶SR|=|A∶S|/|A∩R∶S∩R| 是σ′i-数, 所以SR/R是AR/R的一个Hallσi-子群, 故SR/R=H/R. 由引理3(ii)知,H/R=SR/R在G/R中是σ-半次正规的. 类似地, 我们可以证明BR/R中的任一Hallσi-子群K/R在G/R中是σ-半次正规的. 因此G/R满足定理假设条件, 故由G的选取可知,G/R是超可解群. 步骤2G是可解群. 事实上, 我们只需证明G是σ-可解群. 因为若G是σ-可解的, 则对G的任一主因子H/K, 都有H/K是σ-准素的, 所以存在G/K的某一Hallσi-子群HiK/K, 使得H/K≤HiK/K. 又因HiK/K≅Hi/Hi∩K是超可解的, 故H/K是初等交换的q-群, 对于某个素数q,G是可解群. 下面我们证明G是σ-可解群. 令p是整除|G|的最小素因子, 且不妨假设p∈σ1. 因为G=AB, 所以若A,B都是σ1-子群, 则G是σ1-群, 从而G是σ-可解群, 得证. 下面我们可以假设A,B不全是σ1-子群, 不妨设A不是σ1-子群, 则A中存在Hallσi-子群Ai, 使得Ai≠1且i≠1. 由定理假设,Ai在G中是σ-半次正规的. 若Ai在G中是σ-次正规的, 则由引理1(v)知A≤Oσi(G). 从而由步骤1知G/Oσi(G)是超可解的, 进而G是σ-可解的. 因此, 在任一种情况下, 我们都能得到G是σ-可解的. 从而步骤2成立. 步骤3G中含有唯一的极小正规子群, 记为N. 且N=Oq(G)=CG(N), 对于某个素数q,q∈σi. 由步骤1和步骤2可以直接得到. 步骤4最后矛盾. 如果T在G中是σ-次正规的, 则 T≤Oσj(G)≤CG(N)=N 矛盾. 从而T在G中是半正规的. 故存在G的子群U, 使得G=TU, 且对任意U1≤U有TU1≤G. 显然N≤U, 从而TN1=N1T. 由TN1∩N=N1知T≤NG(N1), 故 T≤NG(N1)∩A=NA(N1) 即|A∶NA(N1)|是σ′j-数. 由j的任意性知|A∶NA(N1)|是σi-数. 与上面的证明类似, 可得|B∶NB(N1)|也是σi-数. 综上所述, 定理4得证. 推论3[3]令A和B是G的子群, 且G=AB. 如果A,B的所有Sylow子群在G中都是半次正规的, 那么G是超可解群.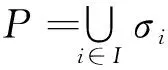
1 预备知识
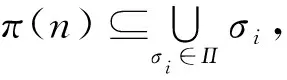
2 主要结果