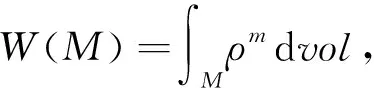n维球空间中的Willmore曲面与Willmore猜想研究综述
王长平,王 鹏
(福建师范大学数学与统计学院,福建省分析数学及应用重点实验室,福建 福州 350117)
子流形的整体几何与拓扑是微分几何领域研究的核心研究方向之一,其中一个代表性的问题为英国数学家Willmore[1]在1965年提出的Willmore猜想:
Willmore猜想Sn中的任何一个二维环面都满足
其中H为其平均曲率向量,并且等号成立当且仅当此环面(相差Sn的一个共形变换)为Clifford环面.
关于Willmore泛函和其变分临界曲面的研究由来已久,历史上最初见于1816年左右法国女数学家Germain关于弹性曲面能量的研究.1920年左右德国几何学家Blaschke及其学生Thompsen已经证明Willmore泛函是共形不变的,并将其变分临界曲面-Willmore曲面- 称为共形极小曲面,其研究成果写入Blaschke关于微分几何的德语专著之中[2].由于Willmore能量是共形不变的,其研究自然成为共形几何研究中的核心问题,吸引了全世界几何学家的研究目光.而在此问题的研究中,数学家们也发展了很多重要的研究工具并开创了新的研究方向,其中一些典型的成果包括:Li等[3]建立了谱几何中的特征值问题和Willmore泛函的不等式,从而第一个给出了这一猜想的部分证明,这一工作已成为了几何分析研究的一个重要部分并被推广到各种情形;Simon[4]第一个利用几何测度论,证明存在Rn中的光滑环面,其Willmore能量为所有浸入二维环面的Willmore能量的最小值; Marques和Neves进一步发展了几何测度论方法,在n=3时完全解决了Willmore猜想,并利用他们的理论证明几何和拓扑研究中的一些其他重要猜想;Bryant[5]研究了Willmore能量临界曲面,即Willmore曲面,给出了二维球面的分类定理,开创了Willmore曲面研究的新领域; Burstall等[6-7]通过四元数分析等方法来研究Willmore球面和Willmore 环面及Willmore 猜想; Kuwert[8]和Rivière[9]等通过曲率流或者PDE方法在Willmore猜想和Willmore曲面研究取得一系列进展,并推动了几何偏微分相关领域的发展.
本文将首先回顾Sn的共形几何,然后简要介绍一下关于Willmore二维球面的研究进展; 接下来回顾以下近年来Willmore猜想研究中的主要进展;关于Willmore猜想在各个方向的推广也是一个重要的主题,将简要介绍一下Willmore猜想的两个推广,即关于Lawson嵌入极小曲面刻画的广义Willmore猜想和关于Willmore超曲面刻画的广义Willmore猜想.
1 Sn中的Willmore曲面

这里H为y在Sn中的平均曲率向量,1则是来自于Sn的截面曲率.称y为Willmore,若它是Willmore能量的变分临界曲面.由Gauss方程可知
由于Willmore能量和Willmore曲面是共形不变的,接下来将回顾一下Sn的射影光锥模型,主要参见文[7,10-11].定义如下同胚:
Sn≅P(L):y↔[(y,1)]=[Y],

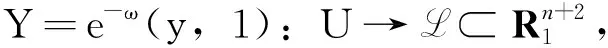
这一子空间与提升Y和复坐标z的选择无关,因此可以定义一个曲面的共形高斯映射[5,13]:
从几何上来看,Vp恰好代表y在p点的二维平均曲率球[5,7,13-14].
选取V⊗C的一个局部标架如下:
其中N∈V满足〈N,N〉=0,〈N,Y〉=-1,〈N,Yz〉 =0.记V⊥为y的共形法丛,ξ∈Γ(V⊥)为法丛V⊥的任意一个截面,D为法联络,则曲面的结构方程如下:

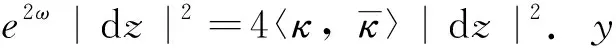
在此标架下,y为Willmore曲面当且仅当Gr为调和映射,当且仅当Willlmore方程成立[5,7,13-14]:
注意到这是4阶椭圆型偏微分方程组,于是 Willmore及相关的几何量均为实解析的.
Bryant的一个重要结果说明,S3中的Willmore曲面均存在对偶曲面,这也是其分类Willmore二维球面的一个核心出发点.在高余维的情形,一般情况下Willmore曲面不再具有对偶曲面,由Ejiri的一个经典结果[11,13-14],如果一个Willmore曲面满足
(1)
则它具有对偶曲面.将所有这样的Willmore曲面称为S-Willmore曲面,注意这与Ejiri原始定义稍有不同,这样定义的好处在于,它恰好刻画了具有对偶曲面的所有的Willmore曲面[11,13-14].
由于Sn中的Willmore曲面一般不再具有对偶曲面,马翔引入了伴随曲面的概念[10-11,14].称y1=[Y1]为y的伴随曲面,若它满足以下3个条件:(1)Y1∈V; (2)〈Y1z,Y1z〉≡0;(3)Y1z≡ 0mod{Y,Y1,Yz} 且V⊥⊗C.关于伴随曲面的详细讨论,参见文[10-11,14-15].
定理1[10]Willmore曲面y的伴随曲面y1=[Y1]:M2→Sn仍为分支Willmore曲面,并且在y1为浸入时,y也是y1的伴随曲面.特别地,若y1退化为单点,或者y1在M的一个开稠集上的平均曲率球和y的平均曲率球重合时,y1为y的对偶曲面.
2 Willmore二维球面
简要回顾一下Willmore二维球面研究的历史.1984年Bryant关于S3中Willmore球面的分类定理[5,16]简洁深刻,从Willmore曲面的整体几何这一研究方向开启了对于Willmore猜想的探索.这一工作对于理解Willmore曲面的分析性质具有重要基础价值.回顾此定理如下:

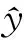
(2)当k=2,3,5,7时不存在这样的极小曲面; 当k取其它值时,存在这样的极小曲面[5,16-17].
Ejiri[13],Musso[18]和Montiel[19]分别从不同角度将Bryant的分类定理推广到S4中的Willmore二维球面.此时新的Willmore二维球面还包括了S4的twistor丛投影到S4中的twistor曲线,将一大类几何中的重要曲面与Willmore曲面研究关联起来.

(1)y为S-Willmore曲面,且属于以下2种曲面之一:
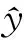
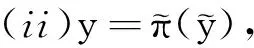
(2)[19]对于以上Willmore二维球面,均有W(y)=4πk; 且对任意k∈Z+,存在S4中Willmore二维球面y,使得W(y)=4πk.
关于Twistor几何的内容,可参见文[13,20-23].
对于更高余维数的情形,Ejiri分类了具有对偶曲面(即S-Willmore)的所有Willmore二维球面,得到了类似的结果,并在论文最后提出公开问题,是否Sn中任何一个Willmore二维球面都是S-Willmore的?
在文[24]中,利用Dorfmeister等关于Willmore曲面的可积系统的研究方法[25-26],给出S6中的第一个非S-Willmore的Willmore二维球面; 在文[27]中,利用文[28]和文[29]等工作,通过可积系统方法给出了Willmore二维球面的一个粗略的可积系统刻画.通过进一步对Willmore二维球面的分析性质的讨论,马翔等给出了S5中Willmore球面的几何分类,并构造了第三类Willmore球面的例子.

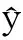


关于此定理的详细讨论,参见文[11].这里简要回顾一下证明的概要.其核心的思想是构造如下全纯微分形式:
由于S2不存在非平凡的全纯形式,因此Θ≡0.进一步利用余维数的限制,可以证明或者S-Willmore条件(1)成立,或者此曲面的法丛有一个整体正交分解:T⊥S2=W1⊕W2,其中W2定义了一个新的整体调和映射,利用此调和映射,可以重新构造出y的伴随曲面y1,并证明其为R5中的某个特殊分支极小曲面.反之, 从R5中的某个特殊分支极小曲面出发,通过求解一个Riccati方程,给出了一些具体的S5的Willmore球面,这些Willmore球面不具有对偶曲面.详细证明见文[11].关于齐性Willmore二维球面分类见文[30].
关于Sn中的一般Willmore二维球面,有如下猜想[11,14]:

(1)Rn中的一个亏格为0的具有平坦嵌入端的完备极小曲面.
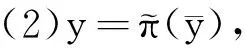
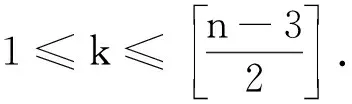
在n≤8时可以证明此猜想成立,但更高维数的时候的由于伴随变换产生的奇点难以消除,需要引入新的方法.
3 关于二维环面的Willmore猜想
本节回顾一下关于Willmore猜想的研究进展.首先将介绍Li-Yau[3]关于Willmore猜想的部分证明的思路,接下来介绍一下Marques和Neves关于S3中的Willmore猜想证明的大致思路,最后大致介绍一下Lawson嵌入极小曲面ξg,1和关于它们的广义Willmore猜想.
3.1 共形面积和Li-Yau关于Willmore猜想的部分证明
在文[3]中Li等引入了共形面积这一基本概念,并成功用于曲面的第一特征值估计和Willmore能量估计,第一个给出了限定共形结构下Willmore猜想的证明.
定义1设(Mm,gM)为一个m维黎曼流形.

(2)记C(M,Sn)为从M到Sn的所有非常值分支共形映射组成的集合.黎曼流形(Mm,gM)的n维共形体积VC(M,n)定义如下:
(3)黎曼流形(Mm,gM)的n维共形体积VC(M,n)定义为:
由定义可知VC(y,n),VC(M,n)和VC(M)为共形不变的.特别地,当M为具有共形度量gM的二维黎曼面,n=2时,VC(y,2)恰好是4πdeg(y).
定理5[3]设M为一个黎曼面,具有共形度量gM.
(1)记λ1为gM的Laplace算子第一特征值,则有
λ1Area(M)≤2VC(M),

这里简要介绍一下证明概要:第一部分的证明核心是利用Sn的共形变换,使得坐标函数可以作为特征值的试探函数,用于估计第一特征值,从而给出结论; 第二部分则是基于Willmore能量和共形面积的共形不变性以及Willmore能量显然大于面积这一简单的不等式.具体证明参见文[3]或文[31]中的第3章3.8 节.
回顾一下二维环面的共形类的如下模空间:令T2(a,b)=R2/Λ, 其中Λ=2πZ+2π(a+bi)Z,a2+b2≥1, 0≤a≤1/2,0 W(y)≥2π2, (3)关于具有其他共形结构的二维环面T2(a,b)的Willmore能量下界估计的近期工作参见文[34]. Marques[35]和Neves[36]关于Willmore猜想的证明,是过去十几年中微分几何研究的重要进展,简要回顾一下其证明的核心概要. 他们的工作的第一个出发点是Urbano关于S3中Clifford二维环面的面积指标刻画: 这里的面积指标5=1+4有着清晰的几何意义:其中4来自于S3的非等距的共形变换导致的极小曲面面积的减少; 1来自于面积变分的Jacobi算子的第一特征值,由于此时第一特征值的重数必须为1.由于通常这一特征值对应的第一特征函数无法给出表达式,因此很难刻画这一方向导致的面积变换.这一困难的解决思路,来源于Ros的这一不等式[38-39]. 此外,由Li-Yau的一个经典结果[3],如果y为一个非嵌入的定向闭曲面,则W(y)≥ 8π.因此要证明Willmore猜想,只需对嵌入曲面证明即可. (2)通过Almgren-Pitts极小极大理论证明存在取得面积极值的嵌入极小曲面,其面积大于等于2π2; (3)利用Ros的结论证明上述曲面的面积≤W(y); (4)在等式成立时,证明此极小曲面的面积指标Index(y)≤5,加上此时曲面亏格不为0(因此非全测地),由Urbano定理可知此时曲面为Clifford极小环面. 关于此定理的进一步细节参见文[35-36,40-41].而进一步利用此方法证明S4中的二维环面的Willmore猜想仍旧具有很多困难,Marques和Neves曾经提出希望有一个Urbano型定理的推广.近期,Kusner等给出了如下推广: 如何将此结果推广到Sn,n≥ 5,或者将其中亏格1的假定改为亏格≥ 1,仍旧是公开问题. 首先回顾一下Lawson嵌入极小曲面ξm,k⊂S3的构造.考虑S3中的两个异面且互相垂直的大圆周: γ={(0, 0,cosθ,sinθ)|θ∈[0,2π]},γ⊥={(cosθ,sinθ,0, 0)|θ∈[0,2π]}. 考虑两个圆周上的点 其中j∈Z2k+2,l∈Z2m+2.则{Pj}将γ均匀分为2k+2个大圆弧, {Ql}将γ⊥均匀分为2m+2个大圆弧.令Γj,1为S3经过Pj和Ql的大圆周.令Γ0,1为S3中的测地四边形P0Q0P1Q1,其边界为连接两个相邻顶点的最短测地线(长度为π/2).于是,由关于边界Γ0,0的Plateau问题的解[43],存在一个极小圆盘δ0,0使得其为S3中以Γ0,0为边界的面积最小曲面.由Schwarz反射定理及Pj,Ql的对称性,将δ0,0关于大圆Γj,1的反射给出了S3中的一个嵌入闭极小曲面, 记为ξm,k.Lawson证明这一曲面是嵌入的,亏格为mk的闭极小曲面,关于此曲面的几何和分析性质,详见文[40,43-47]. 这里简要回顾一下近年来关于ξm,k的几何和分析性质进展: 猜想2Sn中的任何一个亏格为g的二维定向闭曲面M都满足 并且等号成立当且仅当此环面在相差Sn的一个共形变换的意义下等价于ξm,k. (2)Choe等证明[44],Lawson嵌入极小曲面ξm,k⊂S3的第一特征值λ1=2,证明了这些曲面满足关于极小超曲面的第一特征值的Yau猜想[31].关于极小超曲面的第一特征值的研究,参见唐梓洲等关于等参超曲面的重要进展[48],及Brendle的重要论文[40,49]. (3)Kapouleas[45]和Wiygul[50]给出了Lawson极小曲面的几个重要刻画: (i)[45]证明Lawson嵌入极小曲面ξg,1在S3中的面积指标(Morse index)为2g+3,nullity为6. (4)利用以上结果,以及Li-Yau等的共形面积,Kusner和王鹏证明: (ii)Lawson极小曲面ξg,1是Willmore稳定的. 这里I和II分别为M的第一和第二基本形式,H为平均曲率. 当m≥ 3的时候,Willmore超曲面和Willmore子流形的研究变得非常复杂,特别地,此时极小子流形不一定仍是Willmore子流形.关于Willmore子流形的更多研究参见文[52-58],其中文[53]在共形几何框架下给出了Willmore子流形的基本理论,文[52]给出了Willmore子流形的第二变分公式,文[53-56]则分别侧重于从黎曼几何的框架下研究Willmore子流形的Simon型不等式及一般黎曼流形中的Willmore子流形,文[57-58]则是结合等参超曲面理论研究Willmore子流形及相关问题; 此外,在关于空间形式中子流形的积分型不等式方法有一系列相关重要工作,详见文[59],这里由于篇幅问题从略. 这里首先回顾经典的Willmore-Clifford超曲面WTm,k的例子: 2001年,郭震等[52]提出了关于超曲面Willmore泛函的广义Willmore猜想: 目前关于此猜想的研究进展甚微,已知的一个重要的如下定理. 定理10[52]Willmore-Clifford超曲面WTm,k在Sm+k+1中是Willmore稳定的. 一个自然的想法是在一些特殊情形证明这一猜想成立,或者将之前关于经典的Willmore猜想的成功经验用于这一猜想研究,比如: (1)在超曲面具有较好对称性如S1-对称性假定下证明这一猜想; (2)对于具有Sr-叶状结构的超曲面证明这一猜想,这里1≤r≤max{m,k}; (3)Li-Yau定义的关于超曲面的共形体积这一共形几何基本不变量和超曲面的Willmore泛函之间此时也缺少一个自然的关系,如何建立这两者之间的关系式并用于以上猜想的研究,也是一个很有价值的问题,关于此方向的部分工作,参见文[16,60]; 其中
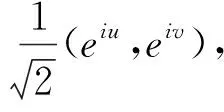
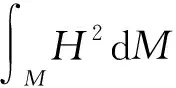
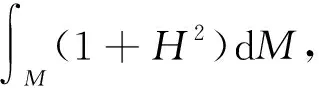
3.2 Marques和Neves关于S3中的Willmore猜想的证明



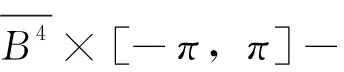


3.3 Lawson嵌入极小曲面和广义Willmore猜想

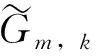
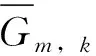


4 Willmore超曲面的广义Willmore猜想