含多吸引子的忆阻混沌系统的分析与实现

曹可，赖强，赖聪

华东交通大学电气与自动化工程学院，江西南昌 330013

自1963年第1个蝴蝶型混沌吸引子Lorenz系统被发现以来，人们对混沌理论的研究与应用的探索已经超过50 a.目前，混沌理论在混沌神经网络［1］、保密通信［2］、图像加密［3-5］、多智能体控制［6］和混沌遗传算法［7-8］等应用方面都有较大发展.1971 年CHUA［9］预测了第4种基本电路器件忆阻器的存在.2008 年，HP 实验室利用TiO2和金属Pt 成功制备了具有忆阻器特性的纳米级二端器件［10］，在实物层面上验证了CHUA的猜测.在此以后，研究者对忆阻器的兴趣更加浓厚.利用忆阻器来构建混沌系统，可以有效增加系统的复杂度和动态特性［11］，因此忆阻器在混沌研究中的应用已受到广泛关注.

目前，忆阻混沌系统的构建方式大致包括两个方向：①忆阻器为主体构建新的混沌系统，即利用不同的忆阻模型辅以较为简单的外围电路构成新系统.LAI等［12］将正弦忆阻器作为额外的反馈控制输入构成了一个忆阻混沌电路，该电路只由包括忆阻器在内的3个器件组成，利用新引入的控制输入让系统产生了极端多稳态现象.XU 等［13］利用忆阻器，记忆电感和线性无源电容构成了具有线平衡点的忆阻混沌系统，可产生共存吸引子等复杂的动力学行为.LI等［14］研究了基于忆阻器串并联构成的具有多稳态的忆阻混沌系统.②向系统直接添加忆阻器，引入忆阻器前原系统大多已存在混沌现象，但忆阻器的应用使系统在混沌行为和动力学特性上产生了不同方向上的改进，提供了具有更复杂动力学行为的高性能系统.阮静雅等［15］将二次型磁控忆阻器作为简化Lorenz系统的正反馈项构建了一个新的超混沌系统，并通过参数调整发现了系统的多吸引子共存和状态转移行为.MA 等［16］提出了一个具有多涡卷吸引子的忆阻混沌系统，该系统利用忆阻器和RCL并联结之间的耦合强度控制混沌现象的产生，最终得出系统中利用忆阻器产生适当程度的正反馈作用可以更有效地触发混沌现象的结论.目前，向混沌系统中引入忆阻器作为系统负反馈项的研究相对较少，且构建的系统大多只具有较简单的动力学特性.但是在混沌保密通信，图像处理等信息加密领域的研究迫切需要高性能的混沌系统.因此，研究具有复杂动力学行为的忆阻负反馈混沌系统有着重要的应用价值和现实意义.目前对于忆阻混沌系统的性质分析主要包括常规性质分析和动力学行为分析，研究发现忆阻混沌电路的特殊动力学行为主要包括共存吸引子［17-19］与极端多稳态［20-21］，隐藏吸引子［22-23］和瞬态转移［24］等现象.这些特性对系统的性能与应用产生了很大影响，所以对具有复杂动力学行为的忆阻混沌系统的分析成为研究热点.

本研究采用磁控忆阻器作为Sprott-J 系统［25］的负反馈项，建立一个具有复杂动力学行为的新忆阻Sprott-J 混沌系统，分析其基本动力学特性和混沌分岔特性，并通过改变系统参数和初始条件，研究系统的吸引子共存现象.基于系统方程设计系统的模拟电路并完成电路仿真验证，证明理论分析结果和电路实验结果吻合，验证了系统的物理可行性，为系统在高性能混沌加密领域的应用提供条件.

1 新忆阻混沌系统构建

对于一个简单的三维混沌Sprott-J 系统，其数学模型可表示为

其中，m和n0为忆阻器参数，n= 3n0.在该忆阻器两端施加不同频率的正弦激励电压v=v1sin(2πft）.其中，v1为电压幅值；f为电压频率.图1为不同电压频率下忆阻器的伏安特性曲线.由图1可见，忆阻器模型的伏安特性曲线符合忆阻器特有的“8”字型磁滞回线.

图1 忆阻器滞回曲线Fig.1 Hysteresis curves of memristor.

对于系统（1），本研究引入磁控忆阻器模型（3）作为系统的非线性负反馈项，构建出新的4维忆阻Sprott-J混沌系统，即

其中，a和b为忆阻混沌系统的可变参数；m和n为忆阻器的可变参数；w为引入忆阻器后的系统第4维度状态变量；ẋ、ẏ、ż和ẇ分别为系统变量x、y、z和w对时间的导数.

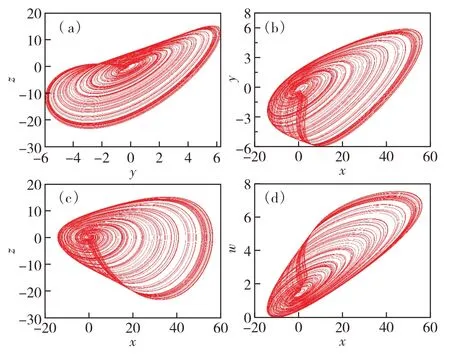
设参数a= 3.6、b= 3、m= 0.2 和n= 0.2，则系 统（4）在 初 始 条 件 [CT1，CT2，CT3，CT4]=[1，1，1，1]时出现混沌现象.图2 为该系统的位于y-z、x-y、x-z和x-w平面上的相轨迹图.

2 新忆阻混沌系统的基本动力学特性分析

对系统（4）进行基本动力学行为分析，包括系统的耗散度、平衡点的存在与稳定性、系统的分岔与混沌特性，以及多吸引子共存现象.

2.1 系统耗散度分析

由耗散度计算公式（5）可得系统（4）的耗散度为∇·V=-2 < 0，即在不同系统参数和初始条件下，系统的耗散度恒小于0，表明系统一直处于耗散状态.其中，V为耗散体积.

2.2 平衡点集与稳定性

分析系统的平衡点集可获得系统在各平衡点上的稳定性，深入了解系统的各项性质.令系统（4）的各微分项等于0，可得平衡状态方程组为

求解方程组（6），可得系统的平衡点集S0={(x，y，z，w)|x=y=z= 0，w=k}.其中，k为任意实数，即系统具有一个线平衡点集.在S0处对系统进行线性化，求得其Jacobian矩阵为

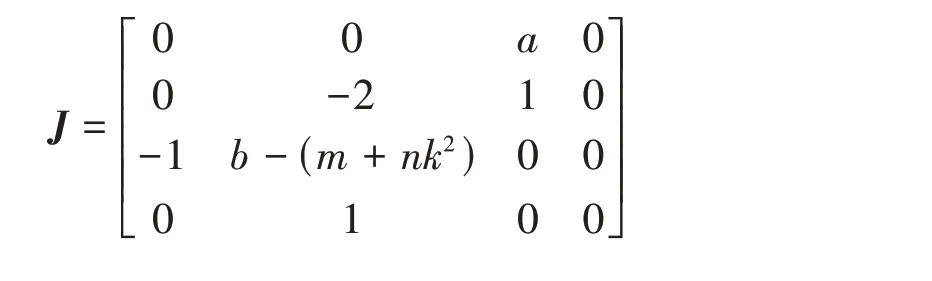
将J带入|J-λE|= 0，求得含有系统参数的特征方程为

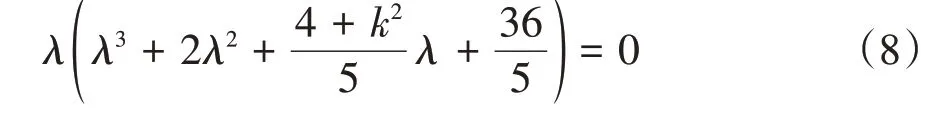
选取k= 0 时的平衡点为S1=(0，0，0，0)，求得此时系统（4）的4 个特征根λ1= 0，λ2=-2.694 6，λ3=-0.347 3 - 1.597 2i，λ4=-0.347 3 + 1.597 2i.其中，λ3和λ4是一对具有负实部的共轭复数根.该平衡点S1是一个不稳定点.当k= 2 时平衡点为S2=(0，0，0，2)，此时系统（4）的4 个特征根分别为λ1= 0，λ2=-2.507 2，λ3=-0.253 6 - 1.675 5i，λ4=-0.253 6 + 1.675 5i.其中，λ3和λ4是具有负实部的共轭复数.该平衡点是一个稳定点.对于一些特定平衡点的分析结果与理论推导相一致，进一步印证了平衡点分析的正确性.

2.3 Lyapunov指数和维数

分析系统的Lyapunov指数，可以得到系统处于不同状态的理论依据.设系统（4）的参数a= 3.6、b= 3、m= 0.2 和n= 0.2，初 始 条 件［CT1CT2CT3CT4］=[1，1，1，1]，则利用Wolf 法计算系统的Lyapunov 指数［27］，可得此时的4 个Lyapunov 指数分别为LE1= 0.168 22、LE2= 0.000 66、LE3=-0.000 77 和LE4=-2.168 10.系统最大Lyapunov指数大于0，且所有指数和小于0，所以该系统是一个混沌系统.

混沌系统的Lyapunov维数为

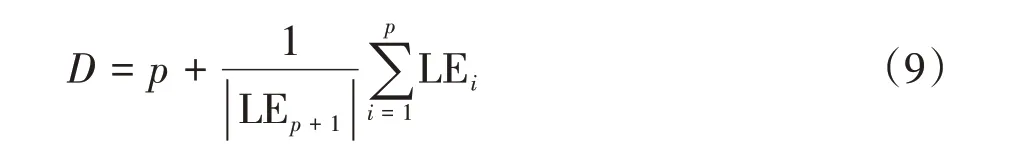
其中，p的值为系统的维数减1，当i取不同值时LEi分别取系统的各项Lyapunov指数值.由式（9）可得，新忆阻Sprott-J 混沌系统D=3.077 5，所以该系统是分数维系统，进一步表明系统是混沌的.

3 新忆阻混沌系统动力行为学分析

利用Matlab 软件的ode45 函数绘制新忆祖Sprotl-J 混沌系统的分岔图和Lyapunov 指数谱，用于分析其混沌分岔特性和参数特性.分析混沌分岔特性时算法的时间区域为［0，1 000］，步长Δt1= 0.01.研究吸引子共存时设置的时间区域为［0，500］，步长Δt2= 0.002.

3.1 改变参数a时系统的混沌分岔特性

固定参数b= 3、m= 0.2 和n= 0.2，设置初始条件为［CT1CT2CT3CT4］=［1，1，1，1］，在［1.5，6.5］区间内改变系统（4）的参数a，得到系统（4）的Lyapunov 指数谱和分岔图如图3.由图3（b）的分岔图观察到系统从混沌进入周期的路径，再综合考虑指数谱可得当a取不同值时的系统状态.当a∈[1.50，1.95]时，系统的最大Lyapunov 指数接近0，此时系统处于周期3 状态；当a∈(1.95，4.67]时，系统的最大Lyapunov 指数在0 ～ 0.3，系统进入混沌状态；当a取值在2.5、3.5 和4.1 附近时，系统出现短暂的周期窗口.随着a的增大，系统的最大Lyapunov 指数接近并最终稳定为0，系统经反倍周期分岔从混沌状态进入周期状态.当a∈(4.67，4.73]时，系统进入周期4 状态；当a∈(4.73，5.69]时，系统属于周期2 状态；当a∈(5.69，6.5]时，系统处于周期1状态.可见，图3所示的分岔图与指数谱现象吻合.

图3 a ∈[1.5，6.5]时系统（4）的（a）指数谱和（b）分岔图Fig.3 (a)Exponential spectrum and(b)bifurcation diagram for system(4)when a ∈[1.5,6.5].

图4为系统（4）在不同a值条件下的x-y平面相轨迹图.由图4可见，当a= 2.15时，系统出现混沌吸引子；当a= 3.1 时，系统混沌轨迹的复杂程度加大；当a= 4.43时，系统的混沌吸引子发生改变；当a= 4.81时，系统出现周期2吸引子，即系统处于周期状态.可见，系统（4）的x-y平面相轨迹图与其分岔图（图3（b））相符.

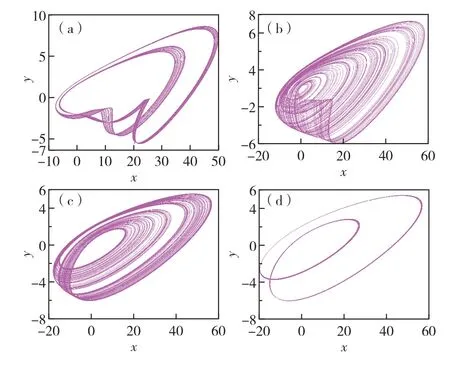
图4 改变参数a时系统（4）的x-y相轨迹图 （a）a = 2.15；（b）a = 3.10；（c）a = 4.43；（d）a = 4.81Fig.4 x-y phase trajectory for system(4)with(a)a = 2.15,(b)a = 3.10,(c)a = 4.43,(d)a = 4.81.

3.2 忆阻器参数m变化时的混沌特性

固定参数a= 3.6、b= 3和n= 0.2，给定系统（4）的初始条件［CT1CT2CT3CT4］=［1，1，1，1］，在［0，2］范围内改变m参数，此时系统的Lyapunov指数谱和分岔图如图5.由图5 可见，随着m的增大， 系统由混沌状态进入周期状态. 当m∈[0，0.65]时，系统存在大于0 的最大Lyapunov指数，此时系统处于混沌状态.当m取值处于0.17、0.32 和0.48 附近时，系统出现小范围的周期窗口.随着m持续增大，系统的最大Lyapunov指数从0.2 逐渐降到0，系统经反倍周期分岔进入周期状态.当m∈(0.65，0.72]时，系统处于周期4状态；当m∈(0.72，1.02]时，系统进入周期2 状态；当m∈(1.02，2]时，系统处于周期1状态.

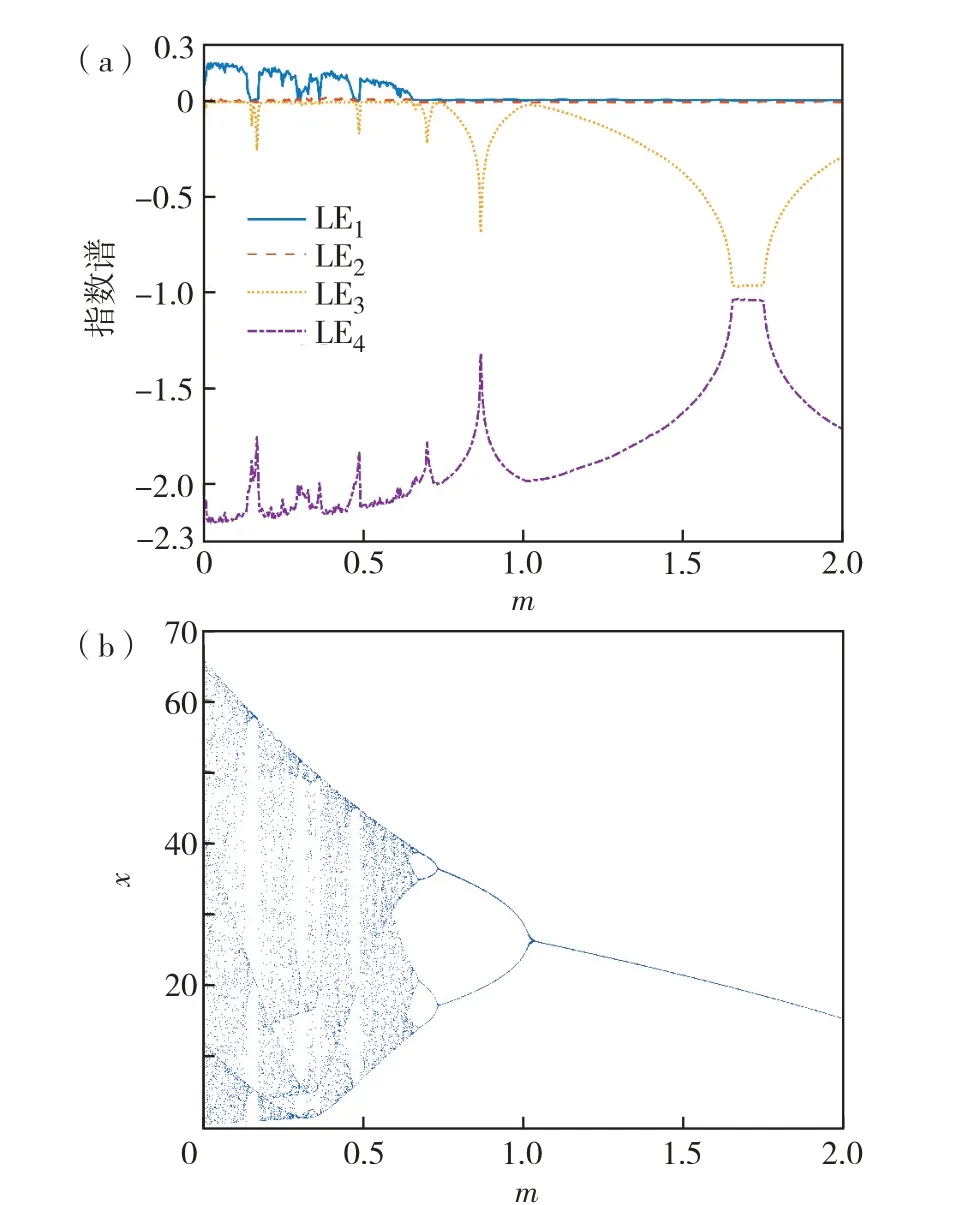
图5 m ∈[0，2]时的（a）指数谱和（b）分岔图Fig.5 （a）Exponential spectrum and（b）bifurcation diagram when m ∈[0，2].

3.3 吸引子共存

对系统（4）在一定参数和初始条件下的动态演化进行研究，发现存在多吸引子共存现象.固定参数b= 3、n= 0.2 和m= 0.2，改变系统初始条件CT4.图6给出了当CT4分别为−1、1.23和1.55，a在［1.5，6.5］内变化时的最大Lyapunov指数图和分岔图.图6（b）中蓝色曲线表示初始条件［CT1CT2CT3CT4］=［1，1，1，−1］时系统的组合分岔图；红色表示［CT1CT2CT3CT4］=［1，1，1，1.23］时系统的组合分岔图；绿色表示［CT1CT2CT3CT4］=［1，1，1，1.55］时系统的组合分岔图.

由图6（a）可见，当初始条件CT4=-1时，系统在a∈[1.5，2.35] 条 件 下 处 于 周 期 状 态；a∈(2.35，5.21]条件下，系统进入混沌状态，系统的最大Lyapunov 指数也在此范围内取得最大值；a∈(5.21，5.63]时的最大Lyapunov指数为0，系统处于周期状态.随着a的持续增大，系统再次进入混沌并在a= 6.45附近出现反倍周期分岔现象.当CT4= 1.23 时，系统在a∈[1.5，2.05]条件下处于周期状态；在a∈(2.05，4.20]条件下出现混沌状态，此范围内也伴随着短暂的周期窗口；在a∈(4.20，6.5]条件下由反倍周期分岔从混沌进入周 期 状 态. 当 CT4= 1.55 时， 系 统 在a∈[1.5，2.07] 条 件 下 处 于 周 期 状 态； 在a∈(2.07，3.64]条件下进入混沌，此时系统的最大Lyapunov指数出现极值；在a∈(3.64，6.5]条件下系统出现反倍周期分岔现象.图6（b）组合分岔图清晰地表现了系统在不同初始条件下从混沌进入周期的路径.相比另外两种取值，当CT4=−1时，系统出现更大的混沌面积和更广范围的混沌分布.可见，系统存在多吸引子共存现象，且初始条件对不同吸引子的混沌特性与分岔现象具有很大影响.

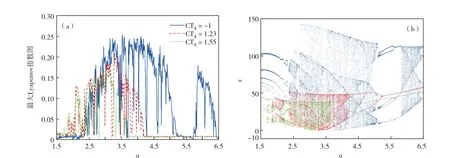
图6 不同CT4时的（a）最大Lyapunov指数图和（b）组合分岔图Fig.6 (a)Maximum Lyapunov exponent diagram and(b)combined bifurcation diagram at different CT4.

图7是不同初始条件（CT4）取值下，a取不同值时系统（4）的x-y相轨迹图.表1 列出了对应情况下系统的最大Lyapunov 指数值.当a= 2 时，3 种初始条件下系统均为周期状态，各初始条件下的最大Lyapunov 指数均接近0；当a分别为2.2 和4.5时，系统出现周期状态与混沌状态共存；当a分别为2.5、3和3.6时，3个初始条件下系统均处于混沌状态，此时系统各状态下的最大Lyapunov指数均大于0.05，出现3种混沌共存现象.分析可得，图7 中不同情况下的相轨迹图与表1 中最大Lyapunov指数的数值大小相符.

图7 不同初始条件CT4对应的x-y相图 （a）a = 2；（b）a = 2.2；（c）a = 2.5；（d）a = 3；（e）a = 3.6；（f）a = 4.5（CT4 =-1的轨迹为蓝色，CT4 = 1.23的轨迹为红色，CT4 = 1.55的轨迹为绿色）Fig.7 x-y phase diagram with changing initial condition CT4.(a)a = 2,(b)a = 2.2,(c)a = 2.5,(d)a = 3,(e)a = 3.6,(f)a = 4.5.(Blue curves are for CT4 =-1,red curves are for CT4 = 1.23,and green curves are for CT4 = 1.55.)

表1 图7中不同吸引子时的最大Lyapunov指数Table 1 Maximum Lyapunov exponents with different attractors in Fig.7

4 电路实现与仿真

为进一步验证系统（4）电路的可行性，采用Multisim 软件设计系统电路并进行仿真分析.图8为本研究设计的3阶磁控忆阻器电路.

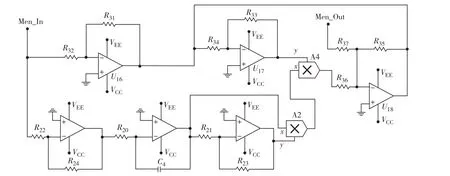
图8 三阶磁控忆阻器电路Fig.8 Three-order magnetic control memristor circuit.

以忆阻器电路模型作为组成部分设计新忆阻Sprott-J 混沌系统的电路.由于系统状态变量范围超过运算放大器的动态放大区，因此，对电路内变量进行均匀压缩，得到（10x，10y，10z，10w）.电路使用增益为0.1 的线性模拟乘法器AD633.利用时间尺度变化联系微分方程和积分常数，取τ= 1 000可得变换后系统（4）的方程为

图9 为采用Multisim 软件设计的忆阻混沌系统在x、y、z维度和忆阻器的w维度的电路原理图，各维度之间通过全局连接实现耦合.其中，C1=C2=C3=C4= 10 nF；R1= 2.781 kΩ；R6= 5 kΩ；R14= 3.33 kΩ；R18= 0.1 kΩ；R15= 100 kΩ；R2=R7=R12=R20= 100 kΩ；R37= 2kΩ；R3=R4=R5=R8=R9=R10=R11=R13= 10 kΩ；R15=R16=R17=R19=R21=R22=R23=R24= 10 kΩ；R31=R32=R33=R34=R35=R36= 10 kΩ.

图9 忆阻混沌系统电路实现 （a）状态变量x；（b）状态变量y；（c）状态变量zFig.9 Circuits of memristive chaotic system for(a)state variable x,(b)state variable y and(c)state variable z.

图10为对图9所示忆阻混沌系统电路进行仿真的示波器结果.对比图10与图2中系统4维度的相轨迹图可以发现，电路实现与数值模拟的结果相一致，验证了新忆阻混沌系统电路设计的准确性.

图10 电路仿真吸引子相图 （a）y-z；（b）x-y；（c）x-z；（d）x-wFig.10 Circuit simulation attractor phase diagrams for(a)y-z,(b)x-y,(c)x-z,(d)x-w.

结 语

设计并研究了一个具有4 个可变参数的4 维忆阻混沌系统.相比原系统，新系统产生了线平衡点集和多共存吸引子，不同于那些只具有限平衡点集的混沌系统.随着参数的变化，系统的出现周期、拟周期和混沌现象，且出现倍周期分岔路径.改变初始条件，系统存在无穷多吸引子共存现象.利用数值分析方法对系统的吸引子共存特性进行了分析，验证了不同初始条件下存在周期共存，周期与混沌共存和混沌与混沌共存的现象.设计了忆阻Sprott-J 混沌系统的仿真电路，观察了电路产生的不同相平面图.比较系统电路仿真现象和数值仿真计算，两者获得了一致的动力学特征表现，验证了该系统的物理可行性，系统可应用于图像加密，保密通信领域.