分段线性忆阻系统的簇发振荡及其机理分析

马铭磷 陈 亮 李志军 王梦蛟 邱志成

(湘潭大学自动化与电子信息学院 湘潭 411105)

1 引言

多时间尺度系统具有广泛的实际应用背景，如神经元放电模型、输电线路不同导线耦合作用、化学反应中不同物质反应速率等[1—4]。簇发振荡(bursting oscillations)是多时间尺度系统中普遍存在的一种复杂动力学行为，表现为大幅振荡与微幅振荡交替出现[5—7]。当系统轨迹表现为大幅振荡时，对应激发态(SPiking state, SP)；当系统轨迹表现为小幅振荡或几乎不变时，对应沉寂态(Quiescent State, QS)，系统轨迹在激发态与沉寂态之间相互转迁时，便形成了这种特殊的簇发振荡模式。对于多时间尺度系统，一直缺少理论分析方法，直到Rinzel[8]提出快慢分析法，才将簇发振荡上升到机理分析的层次。近些年来，国内外学者借助快慢分析法对各种非线性系统的簇发振荡进行了深入研究，并取得了一系列丰富的成果。如，Bao等人[9]揭示了两快一慢莫里斯-勒卡(Morris—Lecar, ML)神经元模型的混沌簇发和多稳态放电模式及其生成机理，并从硬件电路验证了理论分析的正确性；Proskurkin等人[10]研究了化学反应系统中的簇发现象；Han等人[11]研究了参数激励Lorenz系统的簇发行为，报道了由分岔延迟与混沌危机引起的混沌簇发；Ma等人[12]揭示了周期激励Jerk电路中由延迟pitchfork分岔诱发的复杂簇发结构；Han等人[13]在Duffing振子中引入多频参数激励，揭示了turnoverpitchfork-hysteresis与compound-pitchfork诱发的两种新簇发模式；Wei等人[14]研究了参数激励与外部激励联合激励下机械系统的簇发动力学行为，并揭示了由Hopf分岔与同宿分岔引起的复杂级联型簇发模式。

1971年，美籍华裔科学家Chua[15]提出了忆阻器的基本概念，揭示了电荷与磁通之间的关系；2008年，惠普公司研究员首次在物理上制作了忆阻器[16]。由于忆阻器具有独特的非线性和记忆效应，采用忆阻器在神经网络硬件电路中模拟生物突触受到了广泛的关注[17,18]。如，Chen等人[19]采用图解法研究了忆阻型FitzHugh-Nagum电路的簇发生成机理；Lin等人[20]研究了局部有源忆阻器在神经网络电路中的多稳态模式；文献[21]简要阐述了基于忆阻器的混沌、储存器及神经网络电路中的研究进展。最近，一些学者更是研究了忆阻系统中的簇发振荡现象，Wen等人[22]在Jerk电路中引入3次忆阻器模型，在周期参数激励下研究了激励频率与幅值对簇发模式的影响。目前针对忆阻系统的研究，多数学者是基于连续的忆阻系统上，也有部分学者研究了分段光滑模型。如，Wang等人[23]研究了基于2次非线性函数的忆阻器模型及其混沌吸引子, 并设计了分段光滑忆阻器的硬件电路；Ponce等人[24]在一个4D分段线性忆阻系统中发现了多重的focuscenter-cycle分岔；Amador等人[25]分析了一个分段线性忆阻器模型，并在一个3D混沌系统中引入该忆阻模型，揭示了其复杂的动力学行为。

目前，针对忆阻系统的簇发振荡研究相对较少，特别是对于分段线性忆阻系统的簇发振荡现象几乎没有学者进行过研究。分段线性忆阻模型的引入使系统出现了各种非光滑分界面，系统轨迹在穿越非光滑分界面时出现了一些特殊的穿越形式，从而导致整个系统出现了复杂的动力学行为，而传统非线性分析法无法解释这些现象。本文为了揭示分段线性忆阻系统的簇发动力学行为，结合文献[26]中的理论基础，并在一非自治系统中引入分段线性忆阻器模型与外部周期激励项，建立了一种两时间尺度的4D分段线性忆阻系统。借助微分包含定理，在不同系统参数条件下，发现了系统轨迹在非光滑分界面处的突然跃迁与非光滑分岔均会引起系统的簇发振荡，并深入分析了簇发行为的形成机理，为分段线性忆阻器在神经网络中的潜在应用提供了理论依据。

2 数学模型

根据Itoh等人[27]对忆阻器的描述，忆阻器揭示了电荷(q(t))与磁通(φ(t))的关系，忆阻器又分为磁控型与荷控型。本文采用的分段线性磁控型忆阻器为

式中，x, y, z, w为状态变量，其中w为所用分段线性忆阻器的内部状态变量，α, β, γ为系统参数，W(w)为忆导函数，x为忆阻器的输入项，W(x)x为忆阻器的输出项。在不加外部周期激励下，即A=0, 转化为4D混沌系统，在引入外部周期激励后，设定ω=0.01，考虑系统变量x, y, z, w以固有频率O(1.0)振荡，即O(dx/dt, dy/dt, dz/dt,dw/dt)≈O(1.0)≡T1，而周期激励频率ω=0.01≡T2。由于T1, T2存在不同尺度耦合，系统的簇发振荡等特殊的非线性行为便产生了。固定参数a=1, b=2, 分段线性忆阻器特性如图1所示。分段线性忆阻器的引入导致式(3)被分界面(记为Σ: {x,y, z, w|w=±1})分成3个子区域，即区域D—: {(x, y, z,w |w＜—1)}, D0: {(x, y, z, w |—1＜w＜1)}和D+: {(x,y, z, w |w＞1)}，其示意图如图2所示。式(3)的轨迹在不同的子区域会受到不同的子系统控制，当在D—, D0和D+分别受到相应子系统控制时，在相应的子区域有对应的吸引子(包括稳定与不稳定的吸引子)，这里将此种吸引子定义为系统的名义平衡轨迹(Nominal Equilibrium Orbits, NEO)。

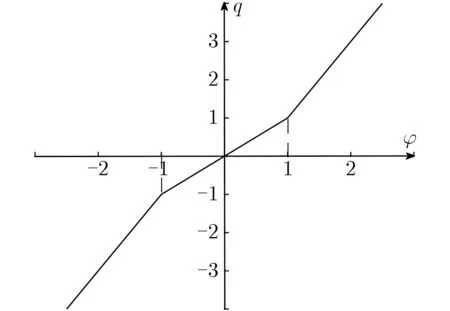
图1 分段线性忆阻器的特性图

图2 (w, z)平面示意图

3 分岔分析

式(3)对应3个子系统相应的Jacobi矩阵记为J—,J0和J+。由于系统向量场在分界面Σ: {x, y, z, w|w=±1}上的不连续，系统轨迹在穿越分界面时可能出现非光滑分岔，借助微分包含理论，引入辅助参数q(q∈[0, 1])，通过Clarke定义[28]得到广义Jacobi矩阵

当辅助参数q从0变化到1时，广义Jacobi矩阵的特征值可以穿过分界面，引起两种余维数为1的非光滑分岔，包含非光滑fold分岔(Non-Smooth Fold Bifurcation, NSFB)与非光滑Hopf分岔(Non-Smooth Hopf Bifurcation, NSHB)。

情况 2 α=7，类似地，可以计算子系统的Jacobi矩阵及其对应的特征根为

在每一个子区域，系统受到该子区域的控制，则有相应的名义平衡轨迹，记为NEO0和NEO±，可以发现在α=7时，子区域D0存在不稳定的鞍焦点，意味着系统轨迹在穿越该区域分界面时，可能会发生非光滑分岔，由于区域D—与D+对应Jacobi矩阵相同，这里仅考虑穿越Σ—1:{x, y, z, w|w=—1}时的情况，引入辅助参数q，其对应的特征方程为

一对纯虚根的出现，意味着可能会产生Hopf分岔，通过计算可知为sup-Hopf分岔。

4 簇发振荡及其机理

因为周期激励频率与系统固有频率存在显著量级差，系统存在两时间尺度效应，当系统轨迹表现为大幅振荡时，对应激发态(SPiking state, SP)，当轨迹表现为微幅振荡或几乎不振荡时，对应沉寂态(Quiescent State, QS)，系统轨迹在激发态与沉寂态之间相互转迁时，便形成了簇发振荡现象。考虑到参数α 的重要影响，分别在两种参数情况下研究系统的簇发行为，即α=4(情况 1)与α=7(情况 2)，并选取适当的激励幅值A，使系统轨迹能够穿越分界面处断层。需要指出的是，所有数值仿真结果都是基于4阶Runge-Kutta算法。

情况 1 设定参数α=4，激励幅值A=0.2，式(3)的(w, z)平面被分界面Σ:{x, y, z, w |w=±1}分成D0和D±3个区域，在每个区域分别有对应的子系统控制的稳定的名义平衡轨迹NEO0和NEO±。

图3给出了α=4时(w, z)平面的相图，z的时序图如图4(a)所示。可以发现，在图3中，(w, z)平面相图被w=±1分成了4个部分，由4个沉寂态(Quiescent States, QSs)与4个激发态(SPiking states,SPs)组成，当系统轨迹遇到非光滑分界面时，运动轨迹会突然跃迁到相应的稳定名义平衡轨迹上，出现激发态，然后逐渐收敛稳定下来，形成沉寂态。在图5中，(x, z)平面相图出现类似涡卷的现象，是由系统轨迹在分界面处的4次跃迁后，逐渐收敛到相应的稳定NEOs形成。由图4(a)的z时序图可知，z的运动轨迹在分界面处的跃迁点在大幅振荡和小幅振荡之间交替进行，图4(b)为状态变量z的局部放大图，T1与T2为运动轨迹收敛到NEOs过程的振荡周期。为了揭示簇发振荡的形成机理，图6把(w, z)平面相图与系统NEO0, NEO±叠加在一起，3支NEOs分别在对应子区域控制3个子系统的运动轨迹。

图3 α=4时(w, z)平面相图

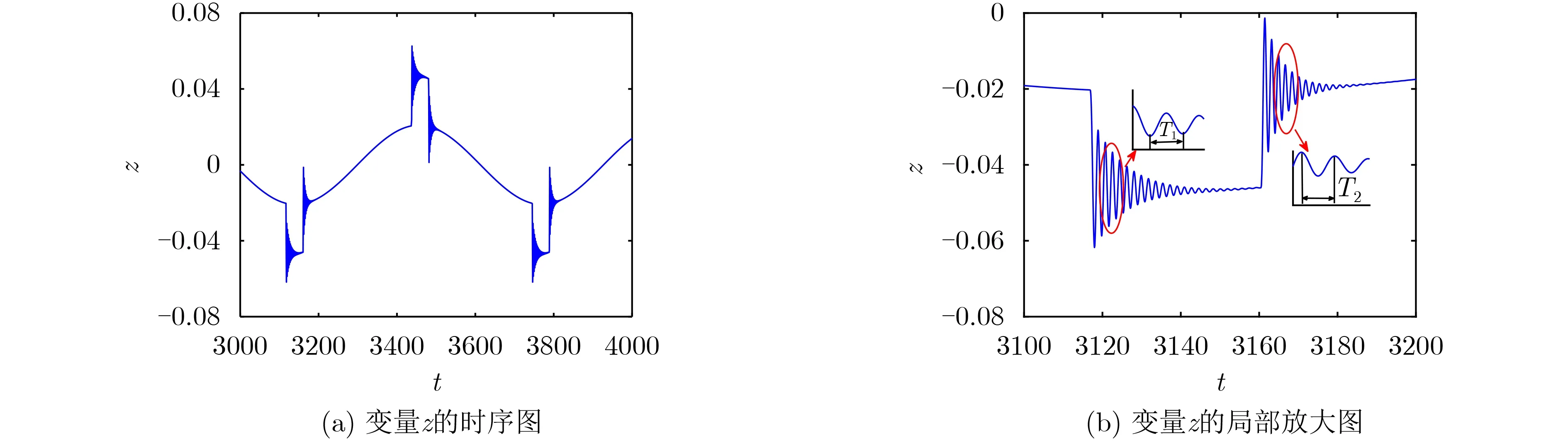
图4 (x, z)平面相图

图5 α=4时变量z的时序图及局部放大图

如图6所示，假设轨迹从P1点出发，沿着NEO0进行小幅振荡并且逐渐稳定在NEO0上形成QS1，因为在子区域D0中NEO0是稳定吸引子，所以系统运动轨迹能够逐渐稳定在NEO0上。当轨迹运动到A1点时，即遇到非光滑分界面Σ—1:{x, y, z, w|w=—1}，由于在子区域D—中NEO—才是稳定的吸引子，轨迹迅速跃迁到了NEO—上，形成了激发态SP1，随后又逐渐稳定到NEO—上形成沉寂态QS2，轨迹严格沿着NEO—运动一直到A3点。同样地，在分界面w=—1处，轨迹迅速跳跃到子区域D0的稳定NEO0上，形成了激发态SP2，然后振幅逐渐减小，最后收敛在NEO0上形成沉寂态QS3，当运动到了A4点，由于分界面w=1的作用，轨迹又迅速跃迁到NEO+上，形成了SP3，接着逐渐稳定到NEO+，然后严格在NEO+上运动直到A2点，同样在分界面Σ+1处发生稳定性交换，轨迹跳跃到NEO0形成SP4，回到P1点，完成一个周期的运动。

图6 α=4时(w, z)平面相图与NEOs叠加图

在频率上，图4(b)为SP2与SP3的局部放大图，轨迹振荡的频率可以近似为子区域D0与D+对应子系统特征值共轭复根虚部的数值。由前面理论计算可知，子系统在D0与D+对应的特征值分别为λ(0)=—0.204±j3.612, λ(+)=—0.126±j3.423, 可知SP2与SP3的振荡频率为ω1=3.612, ω2=3.423。由图4(b)的数值仿真结果计算可知，T1=1.75,ω1N=2π/T1=3.590; T2=1.83, ω2N=2π/T2=3.433。

情况 2 设定参数α=7，激励幅值A=0.2。由计算可知，在子区域D0的特征值为λ(0)=0.0189±j3.472，因此D0对应子系统控制的NEO0是不稳定的，轨迹运动到子区域D0中，不会稳定在该子区域对应的NEO0上，轨迹在穿越非光滑分界面Σ:{x,y, z, w |w=±1}时，可能会产生非光滑分岔。通过前面理论推导，在q=0.984742时，系统会发生非光滑sup-Hopf分岔，形成周期振荡。

图7给出了α=7时，(w, z)平面的相图，由于分界面Σ:{x, y, z, w |w=±1}的存在，系统轨迹由4个SP与2个QS组成，需要指出的是与图3的系统运动轨迹是不同的分岔机理造成的。z的时序图如图8(a)所示，其局部放大图如图8(b)所示，由此可见，在分界面两侧的运动形式不同，振荡的频率也不相同，周期振荡的产生与终止均是由非光滑sup-Hopf分岔形成的。图9显示了(x, z)平面的相图，可以看到系统周期振荡的轨迹。

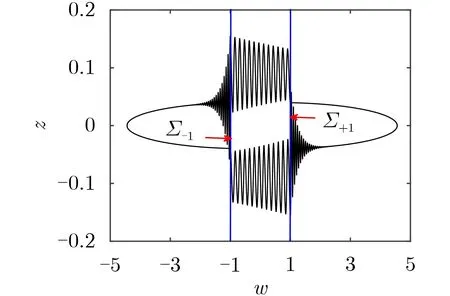
图7 α=7时(w, z)平面相图

图9 (x, z)平面相图

图8(b)可见，轨迹的SP分为左右两边不同的形态，振荡的频率也不相同，在子区域D0中NEO0是不稳定的，轨迹在穿越分界面进入子区域D0后开始周期振荡，在穿出分界面进入D+或D—后结束周期振荡，振荡幅值逐渐减小并缓慢稳定在该子系统控制的稳定NEO上。由前面理论计算可知，由非光滑sup-Hopf产生的特征根为λ(0)=±j3.4499，子区域D+对应一组特征根为λ(+)=—0.175±j3.654 ，因此轨迹在D0和D+振荡的频率为ω3=3.4499,ω4=3.654，由图8(b)的数值仿真计算得，T3=1.806, ω3N=2π/T3=3.479; T4=1.716, ω4N=2π/T4=3.662。

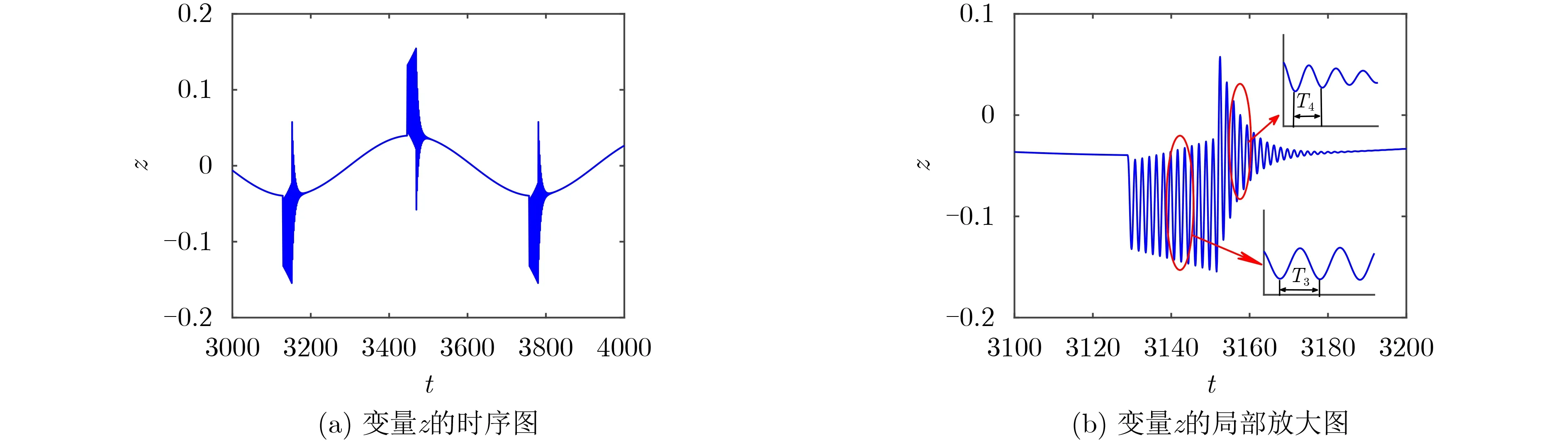
图8 α=7时变量z的时序图及局部放大图

为了更详细地揭示簇发振荡形成的机理及分岔机制，图10将α=7时(w, z)平面相图与对应子系统控制的NEOs叠加在一起。依然假设系统轨迹从P1点出发，在子区域D—中该子系统控制的NEO—是稳定吸引子。

图10 α=7时(w, z)平面相图与NEOs叠加图

因此轨迹能逐渐收敛并稳定下来，沿着NEO—移动形成运动轨迹P1P2，直到遇到非光滑分界面Σ—1:{x, y, z, w |w=—1}上A3点，由于非光滑sup-Hopf分岔的产生，系统运动轨迹开始振荡，形成SP2，因为子区域D0对应子系统控制NEO0是不稳定的，所以运动轨迹在进入D0后并不会收敛到NEO0上，而是因非光滑sup-Hopf分岔产生周期振荡，如P3点，其振荡频率数值上可以近似为特征根λ(0)=±j3.4499的虚部值。轨迹一直振荡，直到遇到非光滑分界面Σ+1:{x, y, z, w |w=+1}上A4点，又因为产生非光滑sup-Hopf分岔，周期振荡消失，随着进入子区域D+，由于D+中子系统控制的NEO+是稳定的，运动轨迹逐渐收敛并稳定在NEO+上，形成运动轨迹P4P5，如P4点，其振荡频率数值上可以近似为D+对应特征根λ(+)=—0.175±j3.654的虚部值。系统轨迹沿着NEO+一直运动到A2点，同样地，再次遇到非光滑分界面w=1，产生非光滑sup-Hopf分岔，进入周期振荡，振荡随着轨迹运动到w=—1的非光滑分界面上，在A1点产生的非光滑sup-Hopf分岔消失，然后系统运动轨迹进入子区域D—，随之收敛到NEO—上到达P1点，完成一个周期的运动。

5 电路仿真

为了揭示分段线性忆阻系统的簇发振荡现象，本文采用混沌电路的模块化设计方法对式(3)在Multisim仿真电路中设计如图11所示电路。运算放大器采用TL082CD实现积分运算与比例运算，模拟乘法器采用AD633AN实现非线性项。所有的有源器件采用±15V供电。在系统参数α=7时，对式(3)的状态方程作时间尺度变换，设时间尺度变换因子τ0=100，并且式(2)忆导模型用W(w)=[1/2sign(|w|—1)+3/2]代替，可得转换后的方程为

图11的电路能够实现式(3)的动力学行为，当系统参数取β=14, e=1.2, γ=0.12, ω=0.01,A=0.2时，相应的电路参数为

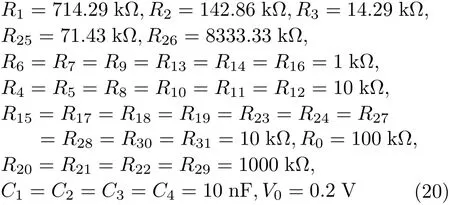
基于Multisim电路平台，设计图11所示电路，保持频率f=ωτ0/2π=0.159 Hz与其他系统参数不变，改变参数α的值，得到α=7(情况 2)与α=4(情况 1)两种参数条件下的不同簇发模式，图12和图13电路仿真结果与Matlab数值仿真结果一致。

图11 分段线性忆阻系统簇发振荡的电路原理图

图12 α=7时Multisim电路仿真图

图13 α=4时Multisim电路仿真图

6 结束语

本文在一非自治系统中引入分段线性忆阻器模型与外部周期激励项，当周期激励频率远小于系统固有频率时，构建了一种两时间尺度的分段线性忆阻系统。由于分段线性忆阻模型的引入，原系统被分成不同的子区域，在每个子区域有相应的控制子系统，系统轨迹在穿越两个子区域的非光滑分界面时，便会产生特殊的动力学行为。基于Matlab数值仿真与Multisim电路仿真，在不同的系统参数条件下，揭示了两种不同的簇发模式；系统在激发态(SP)和沉寂态(QS)之间相互转迁并不像连续系统一样由系统固有分岔产生，而是在非光滑分界面处产生的非光滑分岔与临界条件改变所形成。本文首次对分段线性忆阻系统的簇发动力学行为进行研究，揭示了两种新的簇发模式与分岔机理，进一步丰富了分段线性忆阻系统的簇发路径。