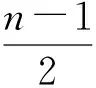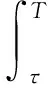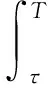具有边界反馈的波方程系统解的能量衰减估计

白忠玉，陈娜娜

(海口经济学院 网络学院，海南 海口 571127)

设Ω是Rn中具有C2边界Γ的有界区域，Γ1和Γ2是Γ上两个不相交的开集，Γ1∪Γ2=Γ.文中研究波方程系统

(1)

其中ν是Γ上的单位外法向量，非负函数

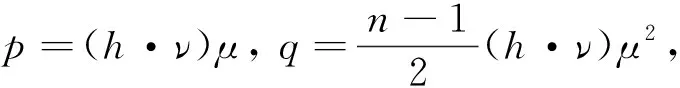
(2)

正函数μ∈L∞(Γ2)，h=h(x)由下面(3)式定义.

任取x0∈Rn，设

h(x)=x-x0,x∈Rn,

(3)

使得

波方程的能量衰减问题已被许多学者所研究.Feng等[1]采用黎曼几何方法讨论了非线性边界条件的波方程的能量衰减.在几何控制假设下，Ammari[2]证明了带有Drichlet边界的波方程的稳定性.对具有耗散边界条件的波方程，可以运用能量法、Lyapunov泛函等研究其能量衰减性[3-5].文献[6-8]利用微分几何法、摄动能量法探讨了几类粘弹性波方程的衰减问题.通过考虑摩擦阻尼或结构阻尼，文献[9-11]获得了阻尼波方程的能量衰减率.文献[12-13]利用算子半群、预解估计得出了具有扩散型边界控制条件的波方程解的适定性与能量衰减估计.

受文献[2]的启发，文中为系统(1)设计特殊的边界反馈，并建立能量衰减不等式.选取控制函数p,q，利用能量乘子法和文献[1-2]的方法，在适当的几何条件下，给出系统(1)的正则性与能量衰减估计不等式.

设

U={u∈H1(Ω):u=0,x∈Γ1},

(5)

对初值(w0,w1)∈U×L2(Ω),系统(1)有唯一解w满足

定义系统(1)解的能量

易知系统是耗散的.因为

所以E(t)是递减的，t∈[0,+∞).

1 预备知识

设系统(1)的解足够光滑，则对∀t∈[0,+∞)，有w(t),w′(t)∈U.在系统(1)的第三个方程两边同时乘以u∈U，并用Green公式在Γ2上积分可得

这样，系统(1)可写为算子形式

(9)

(10)

其中B∈U×L2(Ω)是线性算子，定义为:

U中的欧氏范数定义为

它等价于H1(Ω)上的范数.

由(8),(12)和(13)式易知，B+I是Hilbert空间U×L2(Ω)上的单调算子.当p,q≥0时，对任意的(w,z)∈D(B)，有

任取(u,g)∈U×L2(Ω)，考虑问题

应用Lax-Milgram定理可知(15)有唯一解w∈U.

由(15)式及v∈D(Ω)可知Δw=4w-2u-g∈L2(Ω).因此，(15)式可写成

令z=2w-u，则(w,z)∈D(B)，且

根据B+I的单调性知，B+2I是满射的.

对每个初值(w0,w1)∈U×L2(Ω)，应用Hille-Yosida定理可知，系统(1)有唯一解，使得

(w,w′)∈C([0,+∞);U×L2(Ω)).

(18)

进一步，当t→∞时e-t||(w,w′)(t)||U×L2(Ω)递减.事实上，令

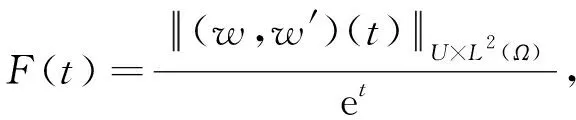
(19)

则由F(t)>0可知，F2(t)和F(t)单调性相同.

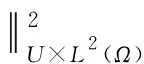
所以只需关注G′(t)-2G(t)的符号.而

于是

从而

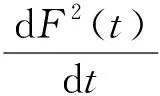
特别地，由(7)和(13)式，有

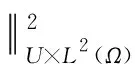
(20)

又D(B)在U×L2(Ω)中稠密，且对每个初值(w0,w1)∈D(B)，系统(1)的解满足

注意到，Γ1∩Γ2=∅,D(B)⊂H2(Ω)×U,Δw∈C([0,+∞);L2(Ω)).进一步，由(21)式可得

2 主要结果

引理1设w是系统(1)的解，且满足(22)式，则当0≤τ

证明用w′乘以系统(1)的第一个方程，在Ω×(τ,T)上分部积分，并由系统(1)的第二、三个方程可得

结合(7)式即得(23)式.

下面证明(24)式.用2h·w+(n-1)w乘以系统(1)的第一个方程，分部积分得

应用Green公式可得

即

由(25)式得

再由系统(1)的第二、三个方程和(7)式即得(24)式.】

定理1设M=sup{|h(x)|:x∈Ω}，则存在μ∈L∞(Γ2)，当μ≥1/M,μ|h|≤1且(2)式成立时，对系统(1)的任意解w及(w0,w1)∈D(B)，满足

证明先证明

应用散度定理和(3)～(4)式可得

利用(2),(7),(29)式和Cauchy-Schwarz不等式得到

下面证明

由(2)式可得

应用Cauchy-Schwarz不等式及μ≥1/M,μ|h|≤1,x∈Γ2，得到

由(4)式可得

结合(2)式可得(31)式.

由(28)和(31)式，有

利用(23)式得到

把上式代入(34)式，并结合(2)式即得

由h·ν≤0,x∈Γ1可得

所以

当T→+∞时，有

(37)

进一步，(37)式可写为

于是

由(7),(23)和(37)式可知，E(t)是非负单调递减的，且

因此

令τ+2M=t，则

此即为估计(26).

当n=2时，(36)式的第二项

将上式右端移到左端，则

于是，当n=2时有

(39)

所以(39)式中w关于t恒为零.

易知

进而

(40)

用与n≠2情形同样的推理方法，可得估计式(27).】