问题解决的概念视角——以2022年高考函数部分试题为例

安徽省金寨第一中学 六安市徐道奎名师工作室 徐道奎 （邮编：237300）

概念是思维的基础，是问题解决的逻辑起点，分析和解决问题要依据概念、围绕概念进行.函数导数问题涉及的概念多，问题解决过程的概念性强，现选择2022年全国高考函数导数试题说明.

1 回归概念的本质

题1（理科甲卷第6题）

当x=1 时，函数取得最大值-2，则f′(2)=_______.

分析试题考查函数单调性、最值等概念.从概念的角度分析,要回归概念所反映的问题的本质，求函数最值需要分析函数图象，要从导数求得函数的单调区间入手.由f(1)=-2，得b=-2.由于，所以当a≥0 时，f′(x)>0，函数f(x)在(0,+∞)上单调递增，没有最大值.a<0 时，函数在上单增，在上单减.所以处取得最大值，故

题目已知函数最大值时自变量的取值，我们在运用概念分析时可以通过导数和图象分析另求自变量取何值时函数取最大值，把题设和用概念分析的结果对应起来.

当然，求出b=-2 后，根据f′(x)=0 解得a=-2，对于解选择题是可以的，但如果求得的a有多个值，则需要检验.而依据最大值的本质（分析单调区间，找最值点）去解决问题则能直击要害，一步到位，这是最严谨和最把稳的.

2 构造运用概念的情境

题2（理科甲卷第11题）

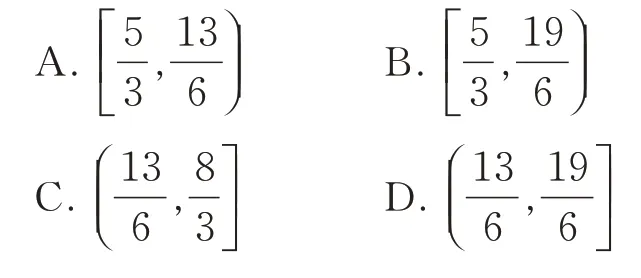
分析试题主要考查函数图象（五点法作图）的概念，同时涉及周期、单调性、极值点、零点等多个概念.因为x∈(0,π)，所以由题意，结合五点法作图可知，函数f(x)在(0,π)上图象如图1.

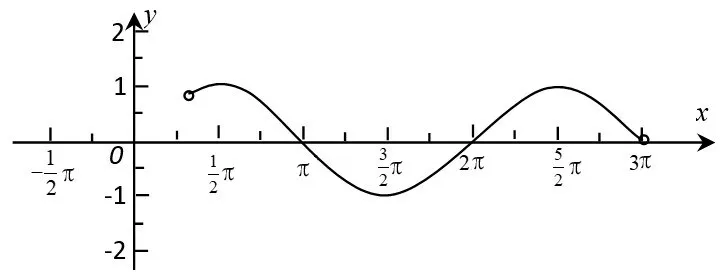
图1

准确作图是充分运用条件的前提，而作图的关键是分析出x=0（此时整体角处于五点法作图的“五点”第一点（整体角ωπ+和第二点（整体角之间.所以，根据最后一个极值点位置可知，

当然，也可以把f(x)在(0,π)上的极值点和零点信息转化为上的极值点和零点处理.

顺利解题，就需要想办法创造运用概念的情境，如本题，只有通过作图，分析出函数图象的起、止点位置，才能找到关系，把条件转化为不等式关系.

3 注重以概念引领变式构造

题3（理科乙卷第12题）

已知函数f(x)、g(x)的定义域均为R，且f(x)+g(2-x)=5，g(x)-f(x-4)=7.若y=g(x)的图象关于直线x=2 对称，g(2)=4，则

A.-21 B.-22 C.-23 D.-24

分析因为问题求的是的值，所以要分析出f(x)满足的关系，想到消去条件中的g(x)，用周期或对称关系解题.

遇复杂关系，不知道条件如何运用时，要想到对其进行转化，条件可能得到什么，如何变换，朝着什么方向努力，实际上是概念在暗中引领，解题的思路也是由概念引发的.

4 准确理解概念之间的逻辑关系

题4（理科乙卷第16题）

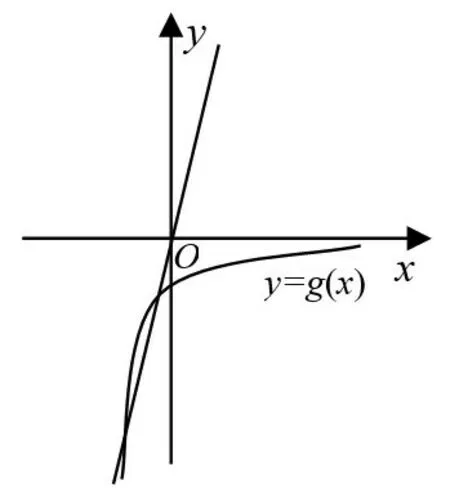
已知x=x1和x=x2分别是函数f(x)=2ax-ex2（a>0且a≠1）的极小值点和极大值点.若x1

分析这是一个概念性非常强的函数导数问题，涉及极值点、导数、导数几何意义、导数变号零点、图象分析等多个概念综合运用.问题的起点低，落点高.

要准确理解函数极值点与其导函数零点之间的关系，导数变号零点的各种不同求法.

由题意和极值点概念，自变量从小到大（图象自左至右），函数依次取极小值和极大值，因此，函数图象自左至右单调性依次为减、增、减，对应的导函数值依次为负、正、负.

现在我们对导数的变号零点进行分析.分析导数变号零点的方法很多，要根据问题的情境进行选择.因为f′(x)=2axlna-2ex，导函数零点可转化为两个函数y1=g(x)=axlna和y2=ex交点（横坐标）.显然y1与y2的图象应该交于两点，且自左至右y1图象在y2图象的下、上、下，先考虑切线斜率，然后考虑割线与切线斜率的关系.

（1）当a>1 时，若y1与y2的图象有两个交点（如图2），自左至右y1图象在y2图象的上、下、上，这时，x1是极大值点，x2是极小值点，不合题意.

图2

图3

（2）当0

5 把握概念的适用条件和概念运用视角

题5（文科乙卷16题）

分析试题考查函数奇偶性概念、性质.要注意概念的适用条件，不能在不知道定义域的情况下代入自变量.有的同学盲目代入（这是最典型的错误），虽然也能得出结果，但其过程是错误的.

法一从具有奇偶性的函数其定义域是关于原点的对称区间的角度分析.

一个概念往往有多种理解方式，要善于在复杂情境中选择最适合解决问题的概念运用方式，因此，要提升对概念的理解水平和综合运用能力.

概念是思维的逻辑起点，是思维的源泉，依据概念的内涵和意义，从不同角度切入概念，问题的解决方法不同，但所有问题解决都是建立在概念运用基础之上.

6 强化概念运用意识，找准概念运用的切入点

题6（新高考卷1 第15题）

若曲线y=(x)+aex有两条过坐标原点的切线，则a的取值范围是______.

分析本题主要考查函数切线的概念，最终转化为零点（方程的解）解决，在问题解决过程中，切点是关键.

设切点为(x0,y0),则y0=(x0+a)ex0,切线斜率k=(x0+1+a)ex0,因此，切线方程为：y-(x0+a)ex0=(x0+1+a)ex0(x-x0),又由于切线过原点，所以-(x0+a)ex0=-(x0+1+a)ex0x0,整理得：x02+ax0-a=0,因为切线有两条，所以Δ=a2+4a>0,解得a<-4或a>0,所以a的取值范围是(-∞,-4)⋃(0,+∞).

解决问题要从概念入手，一开始，不要盯着“两条切线”，而要抓住切线概念.先求切线.切点是应用切线概念的关键，通过设切点，求切线，得到参数关系，自然而然知道如何处理“两条切线”的问题，从而使问题解决.

7 注重概念综合运用

题7（新高考1 卷第12题）

已知函数f(x)及其导函数f′(x)的定义域均为R，记g(x)=f′(x)，若，g(2+x)均为偶函数，则（）.

分析本题为多选题，考查抽象函数奇偶性、对称性、周期性以及函数与导函数之间的关系等概念，是概念的综合运用.

第一，要准确理解概念的本质.函数奇偶性反映了函数图象的对称特征，函数奇偶性概念的本质是“自变量相反”时“函数值相反（或相同）”，而函数中的“自变量”均是“x”，而不是，因此，（*），g(2+x)=g(2-x)，所以，函数f(x)、g(x)的图象分别关于直线,x=2 对称.（*）式中令，可知选项C 正确.

第二，要结合概念充分挖掘条件隐含的信息.由于g(x)是f(x)的导函数，且是函数f(x)的对称轴（f(x)可导，是函数f(x)极值点），所以

第三，要准确把握概念之间的关系.函数与其导函数的对称性有一定关系.由关于直线对称），两边对求x导，得（f′(x)关于点对称）即

由题目的条件可以变出很多结论，但其关键条件仅就两个，即函数f(x)关于直线对称，函数g()x关于直线x=2 对称，根据上述分析，我们完全可以构造函数f()x=sin πx+1（该函数符合题目中的所有条件），则g(x)=π cos πx，这样可将选项A 和D 排除，这也是以特殊的关系运用概念.

运用概念时，要对题目的条件进行变式转化，由函数的两个对称关系推出周期，或由一个对称和周期推出其它对称都属于最基本的变式.

概念反映了数学的本质，概念在问题解决中的作用不可替代，因此，要有以概念解决问题的视角，强化概念解决问题的意识，提升用概念解决问题能力.