幂等矩阵的性质及应用

◎任芳国 和嘉琪

(陕西师范大学数学与统计学院，陕西 西安 710119)

一、引 言

幂等矩阵是一类常见的较特殊的矩阵，在矩阵理论中具有重要的地位和作用，它的很多优良的性质对解决矩阵问题大有益处.它不但在高等代数中有着重要的应用，在其他课程里，如计量经济学、统计学课程中也有重要应用.幂等矩阵及其相关性质具有鲜明的背景、丰富的理论，但是在通常的高等代数的教材中关于幂等矩阵的讨论是比较少的，因此，本文在前人已有的研究基础上对幂等矩阵的性质做了一些有益的补充和推广，就幂等矩阵的性质给予系统的归纳、分析和证明.

为了本文讨论更方便需要以下定义和引理.

1设∈×，的行向量组的秩或列向量组的秩称为矩阵的秩或者矩阵的非零子式的最高阶数称为矩阵的秩，记作()，并规定零矩阵的秩为0.

2设∈×，集合{|∀∈}称为的值域，记作()；集合{∈|=0}称为的核，记作().

3设∈×，如果的秩等于它的列(或行)数，称是列(行)满秩矩阵，特别地，可逆矩阵也称为满秩矩阵.

4设∈×且()=，如果存在列满秩矩阵∈×及行满秩矩阵∈×，使得=，称矩阵具有满秩分解.

5设∈×.

(1)如果=，称是幂等矩阵.

(2)如果=，称是对合矩阵.

1(Douglas引理)

设∈×,∈×，则()⊆()⟺存在∈×，使得=

由()=(,…,),()=(,…,)，其中,分别是与的第个列向量，如果()⊆()，则向量组,…,可由向量组,…,线性表示，那么存在∈×，使得(,…,)= (,…,)，即=；反之结论成立.

2设,是阶方阵,则()=.(证明略)

3设∈×，(),()∈[]，如果((),())=1，则(())+(())=+(()()).

故由等价矩阵的秩不变可知，

4 设∈×,∈×,∈×.如果是列满秩矩阵，是行满秩矩阵，则()=()=()=().

5

(满秩分解)每一个非零矩阵都有满秩分解.

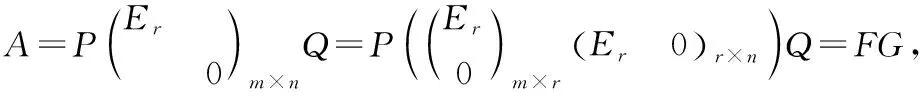
二、主要定理

1设∈×是幂等矩阵，则:

(2)可逆当且仅当是单位矩阵.

(3)()=(-).

(4)∀∈()，有=

(5)()⊕()=.

(7)()=().

(8)的特征值是0或1.

(9)+是可逆矩阵，其中是不等于0,1的任意数.

(10)的最小多项式是或-1或(-1).

(11)能表示成两个对称矩阵的乘积.

(12) 设∈×，则=⟺()⊆().

(13) 设∈×，则=⟺()⊆().

(14)的经典伴随是幂等矩阵.

()==()=()=；

()=()=.

(2)若是单位矩阵，显然可逆；反之，若可逆，由是幂等矩阵知，==()===.

(3)∀∈()，有(-)=-=-0=∈(-)，则()⊆(-)；∀∈，由((-))=(-)=(-)=0=0知，(-)⊆()，所以()=(-).

(4)∀∈()，存在∈，使得=，则=()===

(5)∀∈，由=+(-)=+(-)及()=(-)可知，=()+()；∀∈()∩()，即∈()且=0，于是由(4)知，==0，那么()∩()=0，所以()⊕()=.

(6)由于是幂等矩阵，由dim()=,dim()=-，取()中的一组基,…,，取()中的一组基+1,…,，那么由(5)知，,…,,+1,…,就是中的一组基.

令=(,…,,+1,…,)，则阶方阵可逆，进而由(4)知，

=(,…,,+1,…,)

=(,…,,0,…,0)

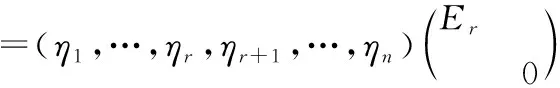
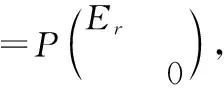
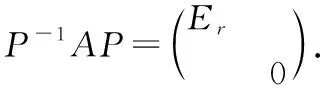
(7)由相似矩阵有相同的迹，并结合(6)知，()=().

(8)由相似矩阵有相同特征值，并结合(6)可知，的特征值是0或1.

(10)由于相似矩阵的最小多项式相同及分块对角矩阵的最小多项式是主对角线上每个子块的最小多项式的最小公倍式，则由(6)知，的最小多项式是或-1或(-1).

(12)充分性：∀∈，由幂等矩阵值域性质(4)及()⊆()知()=()=，所以=；

必要性：若=，由Douglas引理知，()⊆().

(13)充分性：∀∈，由幂等矩阵核性质(3)及()⊆()知，0=((-)) =(-)，即=()，所以=；

必要性：若=，显然()⊆().

(14)由引理2知，=()=()==()，即是幂等矩阵.

综上，定理1得证.

由定理1(12)、(13)易得如下推论.

设,∈×是幂等矩阵，则

(1)=⟺()⊆().

(2)=⟺()⊆().

2设∈×，=()且=是的满秩分解，则下列条件等价.

(1)是幂等矩阵.

(2)()+(-)=

(3)=.

(4)若=≠0，其中,∈，则是幂等矩阵，当且仅当=1.

(5)2-是对合矩阵.

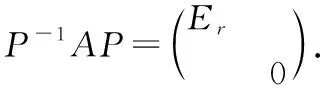
(7)设∈×，则是幂等矩阵,当且仅当存在∈×，使得=，其中=

(1)⟺(2)

取()=,()=-1，显然有()=，()=-，()与()互素，于是由引理3知，()+(-)=(())+(())=+(()())=+((-))，因此()+(-)=，当且仅当((-))=0，当且仅当(-)=0，即=

(1)⟺(3)

必要性：由引理4知，(-)=(-)=((-))=(-)，于是=，当且仅当(-)=0，当且仅当(-)=0，当且仅当=.

(1)⟺(4)

由于≠0，则,都是非零维列向量，那么=是的满秩分解矩阵，于是由(1)与(3)等价知，是幂等矩阵，当且仅当=1.

(1)⟺(5)

由于(2-)=4-4+，则2-是对合矩阵，当且仅当4-4+=，当且仅当4-4=0，当且仅当=

(1)⟺(6)

(1)⟺(7)

充分性：如果=，则由=知，===

必要性：由()=()及Douglas引理知，存在∈×使得=，则有()=()=().设=是的满秩分解，由()=()，即()=()，则由引理4知，()=()，那么是行满秩，再由=，即=及引理4知，

0=(-)=((-))=((-))=((-))=((-))=((-))，即=

综上，定理2得证.

3设,∈×是幂等矩阵.

(1)幂等矩阵是相似不变量.

(2)幂等矩阵具有直和不变性.

(3),∈相似，当且仅当它们迹相同.

(4)按照相似分类，所有的阶幂等矩阵可以分为(+1)类.

(5)-是幂等矩阵，当且仅当==

(6)+是幂等矩阵，当且仅当==0.

(7)如果=，则是幂等矩阵.

(8)若存在两个非零复数,且+≠0使得+可逆，则对所有满足+≠0的非零复数,，线性组合+都是可逆的.

(9)-是可逆矩阵，当且仅当-,+-都可逆.

(10)+是可逆矩阵，当且仅当+,+-都可逆.

(1)设∈×是任意给定的可逆矩阵，令=，则=()===，所以幂等矩阵是相似不变量.

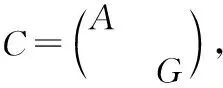
(3)相似矩阵具有相同的迹，又由幂等矩阵的迹等于它的秩，由定理2(6)幂等矩阵的相似标准形及相似关系是等价关系知，两个幂等矩阵,相似当且仅当它们迹相同.

(4)由定理2(6)可知，两个阶幂等矩阵相似，当且仅当它们有相同的秩，对阶幂等矩阵其秩有(+1)种选择，即=0,1,…,，所以，所有的阶幂等矩阵可以分为(+1)类.

(5)必要性：由(-)=--+=--+=-，即

2=+

(3.1)

将上式分别右乘和左乘，则有2=+，2=+，

所以=，再由(3.1)知，==

充分性：因为==，则(-)=--+=-2+=-

(6)必要性：由(+)=+++=+++=+，即

+=0.

(3.2)

将上式分别左乘和右乘，则有+=0,+=0，

所以=，再由(3.2)知，==0.

充分性：因为+=0，则(+)=+++=+=+

(7)由于=，则()====

(8)由∀∈(+)，有(+)=0，即有=-①

将①式两边分别左乘,可得=-,=-②

则由①②可得，=,=③

将=,=代入上式可得

由于+可逆，将上式两边左乘(+)-1得(+)=(+)=+④

将④左乘，得+=+，即=，

将它代入②中的=-可得(+)=0⟹=0=，

再由③式有=0，因此由④式可得(+)=0，

但+≠0，所以=0，

因此(+) ={0}，从而+是可逆的.

(9)由于,是幂等矩阵，有-=(-)(+-)，所以-是可逆矩阵，当且仅当-,+-都可逆.

(10)由于,是幂等矩阵，有+=(+)(+-)，所以+是可逆矩阵，当且仅当+,+-都可逆.

综上，定理3得证.

三、结束语

幂等矩阵是高等(线性)代数教与学的重点内容之一，研究幂等矩阵可以加强对高等(线性)代数的学习和研究.本文主要在高等(线性)代数教学的基础上，总结并深化了关于幂等矩阵的重要性质及一些应用.首先对幂等矩阵的基本的重要的性质进行了归纳总结，并给出幂等矩阵的等价刻画，接着讨论了矩阵普通加法与数乘对幂等矩阵的影响，并进一步获得了幂等矩阵的运算性质，最后讨论了幂等矩阵的分解形式.