图的哈密尔顿性的Aα-谱条件

何 焕，叶淼林

（安庆师范大学 数理学院，安徽 安庆 246133）

本文考虑的所有图都是简单无向图。设G=(V,E)为n阶图，其顶点集V=V(G)={v1,v2,v3,…,vn}，边集E=E(G)={e1,e2,e3,…,em}。图G的邻接矩阵记为A(G)，图G的度对角矩阵记为D(G)。图G的顶点v的度是指G中与v关联的边数目，用dG(v)表示，记δ为G的顶点的最小度。记Kn、K1,n-1、Km,n-m分别是n阶完全图、星图、完全二部图。文献[1]最先给出了Aα-谱的概念，对于任意的实数α∈[ 0,1 ]，称Aα(G)=αD(G)+( 1-α)A(G)为图G的Aα-矩阵。设Aα(G)的n个特征值从大到小排列为λ1(Aα(G))≥λ2(Aα(G))≥λ3(Aα(G))≥…≥λn(Aα(G))，最大特征值λ1(Aα(G))称为G的Aα-谱半径，记为λ(Aα(G))。设G1=(V1,E1)与G2=(V2,E2)是两个顶点不交的图，它们的并图为G1⋃G2=(V1⋃V2,E1⋃E2)，又记为G1+G2；它们的联图记为G1∨G2，即在G1+G2中添加由G1中每个顶点到G2中每个顶点的边所构成的图。一条包含图G中所有顶点的路称为哈密尔顿路，如果图G中任意两个顶点都被一条哈密尔顿路相连，则称G是哈密尔顿-连通的。一个包含图G中所有顶点的圈被称为哈密尔顿圈。如果图G包含一个哈密尔顿圈，则称G是哈密尔顿图。如果图G含有哈密尔顿路，则称G是可迹图。文中没有提到的概念和术语可参考文献[2]。

图的哈密尔顿问题是一个经典且困难的问题，近几年来关于这类问题的研究较多。Fiedler等根据图的邻接矩阵或其补图的谱半径给出了图含有哈密尔顿路或哈密尔顿圈的充分条件[3]。周波利用图的补图的无符号拉普拉斯矩阵的谱半径，给出了图包含哈密尔顿路和哈密尔顿圈的一些条件[4]。Butler等建立了一个图是哈密尔顿的充分条件，即拉普拉斯矩阵的非平凡特征值充分接近于图的平均度[5]。余桂东等根据图的邻接矩阵或无符号拉普拉斯矩阵或其补图的谱半径，给出了图是哈密尔顿-连通的一些谱充分条件，同时利用无符号拉普拉斯谱半径，给出了图含有哈密尔顿路或哈密尔顿圈的条件[6]。受文献[6]启发，本文给出了具有最小度数条件的连通图是哈密尔顿-连通的、哈密尔顿的和可迹的谱充分条件。

1 预备知识

下面介绍需要用到的相关概念和引理。

给定一个含n个顶点的图G，如果对应于Aα-特征向量X={X1,X2,X3,…,Xn}T的特征值是λ，则根据Aα-特征值的定义，当且仅当X≠0，且对于每个u,v，显然矩阵的特征等式为

2 主要结果

受无符号拉普拉斯谱半径与哈密尔顿性的启发，本文想要寻找Aα-谱半径与哈密尔顿-连通性之间的关系，又因为利用图的边数去刻画谱充分条件比较简单，所以借助上面的引理条件得到了下面的结论。

假设G不是哈密尔顿-连通的，则由引理2可得G∈NP1。

如果G=K4∨4K1，则设X={X1,X2,X3,…,X8}T是Aα(G)的特征值λ(Aα(G))所对应的特征向量。由图G的Aα-特征等式（1）可知，所有度为7的顶点在X中对应的值相同，记为X1；所有度为4的顶点在X中对应的值相同，记为X2。仍由图G的Aα-特征等式（1），令λ=λ(Aα(G))，有

将式（2）转化成矩阵等式(B-λI)X′=0，这里X′=(X1,X2)T，

如果G=K4∨(K1,4+K1)，则设X={X1,X2,X3,…,X10}T是Aα(G)的特征值λ(Aα(G))所对应的特征向量。由图G的Aα-特征等式（1）可知，所有度为9的顶点在X中对应的值相同，记为X1；所有度为8的顶点在X中对应的值相同，记为X2；所有度为5的顶点在X中对应的值相同，记为X3；所有度为4的顶点在X中对应的值相同，记为X4。仍由图G的Aα-特征等式（1），λ=λ(Aα(G))，有

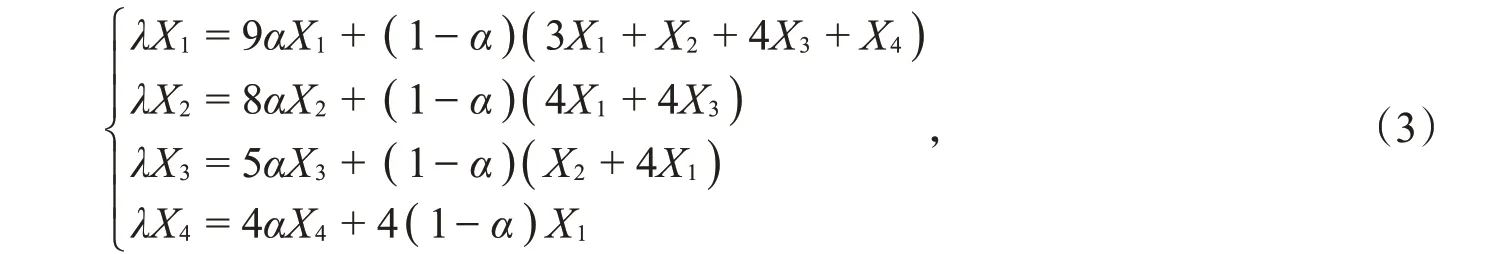
将式（3）转化成矩阵等式(B-λI)X′=0，这里X′=(X1,X2,X3,X4)T，

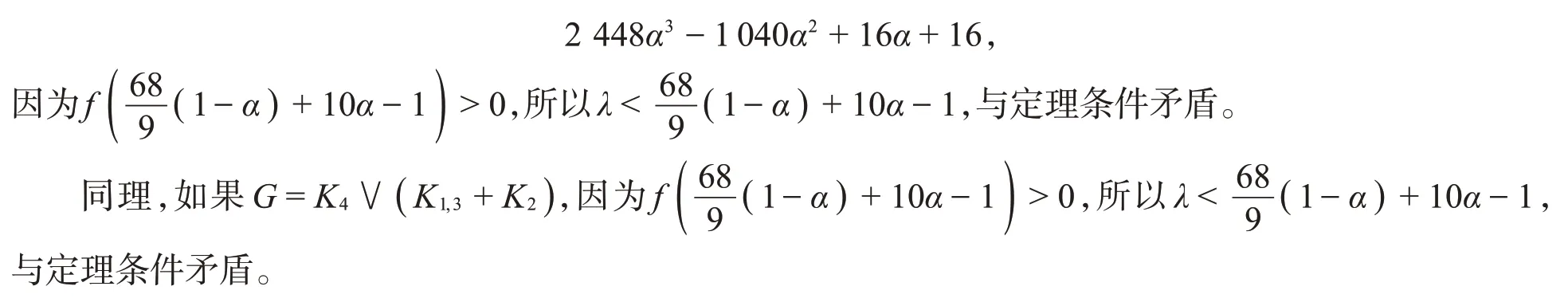
如果G=K3∨(K1,3+K1)，则设X=(X1,X2,X3,…,X8)T是Aα(G)的特征值λ(Aα(G))所对应的特征向量。由图G的Aα-特征等式（1）可知，所有度为7的顶点在X中对应的值相同，记为X1；所有度为6的顶点在X中对应的值相同，记为X2；所有度为4的顶点在X中对应的值相同，记为X3；所有度为3的顶点在X中对应的值相同，记为X4。仍由图G的Aα-特征等式（1），令λ=λ(Aα(G))，有

3 结论

目前，利用邻接谱半径、无符号拉普拉斯谱半径、拉普拉斯谱半径去刻画图的哈密尔顿-连通性、哈密尔顿性和可迹性是十分常见的，比如文献[6]就是利用无符号拉普拉斯谱半径去刻画图的哈密尔顿性。但是，利用Aα-谱半径去刻画图的哈密尔顿-连通性、哈密尔顿性和可迹性的文献较少。本文借助文献[6]的思想，通过刻画Aα-谱半径，给出了具有最小度数条件的连通图是哈密尔顿-连通的、哈密尔顿的和可迹的谱充分条件。今后，希望可以找到一种较为合适的方法来利用Aα-谱半径去判断图的这些性质，从而优化本文中的一些结论。