幂等元集为正规带的r-宽大半群

彭 娇，宫春梅

(西安建筑科技大学 理学院，陕西 西安 710055)

正则半群是半群代数理论的重要研究对象.作为正则半群的推广，1982 年，Fountain[1]引入Green ∗关系，定义了富足半群.1990 年，Lawson[2]在半群上定义了Green～关系.为了将广义正则半群在rpp 半群中做进一步推广，2011 年，郭聿琦等[3]首次提出Green ∗,∼关系，定义了r-宽大半群.

半群幂等元集的性质对半群代数结构有着重要影响.在文献[4]中，Yamada 研究了幂等元满足置换恒等式的正则半群，并讨论了这类半群的结构定理.郭小江在文献[5～6]中分别给出了满足置换恒等式的强rpp 半群和富足半群的结构.在此基础上，文献[7]建立了幂等元满足正规带的半富足半群的结构.文献[8]利用拟织积建立了Uσ-富足半群的结构.文献[9]给出了具有真核的正则ω2-半群的结构定理和相应的同构定理.本文则研究了幂等元集为正规带的r-宽大半群的结构，给出了r-宽大半群的幂等元集为正规带的结构刻画.

文中未出现的记号和术语见文献[10].

1 若干准备

引理 1[3]令S为一半群，E(S)为半群S的幂等元集，且a,b∈S.则下列2 款成立：

(ⅰ)aL∗，∼b当且仅当关于任意x,y∈S1，ax=ay⇔bx=by；

(ⅱ)aR∗,∼b当且仅当关于任意f∈E(S)，fa=a⇔fb=b.

一般情况下，L∗，∼是右同余，而 R∗，∼不 是左同余.L ⊆L∗⊆L∗，∼，R ⊆R∗⊆R∗,∼.

引理 2[3]令S为一半群，E(S)为半群S的幂等元集，且a∈S,e∈E(S).则下列2 款成立：

(ⅰ)aL∗，∼e当 且仅当ae=a，且关于任意x,y∈S1,ax=ay⇒ex=ey；

(ⅱ)aR∗,∼e当 且仅当ea=a，且关于任意f∈E(S),fa=a⇒fe=e.

引理 3[3]令S为一半群，E(S)为 半群S的幂等元集，且e,f∈E(S).则下列2 款成立:

(ⅰ)eL∗，∼f当且仅当eLf；

(ⅱ)eR∗,∼f当且仅当eRf.

称半群S为r-宽大半群[3]，如果S中的每一 L∗，∼-类和 R∗，∼-类至少包含一个幂等元；称r-宽大半群S为弱适当半群[11]，如果它的幂等元集E(S)是 一个半格；称r-宽大半群S为拟弱适当半群，如果它的幂等元集E(S)构 成子半群，即E(S)是 一个带.称带B为正规带[10]，如果带B满足恒等式e fgh=egfh.

对于弱适当半群S，因为E(S)为 半格，所以S的每一 L∗，∼-类和每一 R∗，∼-类有且仅有一个幂等元.含元素a的 半群S的 L∗，∼-类和 R∗，∼-类分别记作La∗，∼和Ra∗，∼.此外，元素a∗和a+分别表示La∗，∼和Ra∗，∼中的幂等元.显然a=aa∗=a+a.

称半群同态α：(S,E(S))→(T，V)为允许同态，如果对于任意a,b∈(S，E(S))，aL∗，∼b蕴含α(a)L∗，∼α(b)，aR∗，∼E(S)b蕴 含α (a)R∗，∼Vα(b)且 α(E(S))⊆V.自然地，我们称(S,E(S))上 的同余ρ 为允许同余，如果自然同态 ρ♮：(S,E(S))→((S,E(S))/ρ,E(S)/ρ)为允许同态.

对于r-宽大半群 (S,E(S))上的允许同态有以下引理：

引理 4令θ:(S,E(S))→(T,V)是一个半群同态，且θ(E(S))⊆V.则 θ为允许同 态当且仅当对任意a∈(S,E(S))，存在幂等元e∈La∗，∼∩E(S)，f∈Ra∗,∼∩E(S)，使得θ(a)L∗，∼θ(e)，θ(a)R∗，∼Vθ(f).

证明显然，必要性成立.下证充分性.假设a，b∈(S，E(S))且aR∗，∼E(S)b.因为 (S，E(S))为r-宽大半群，则存在幂等元f，g∈E(S)，使得aR∗，∼E(S)f，bR∗，∼E(S)g.显然，fR∗，∼E(S)g.据引理3，fRg.又因为 θ是一个半群同态，则θ(f)Rθ(g)，故有θ(f)R∗，∼Vθ(g).据假设，θ(a)R∗，∼Vθ(f)，θ(b)R∗，∼Vθ(g)，故θ(a)R∗，∼Vθ(b).这表明aR∗，∼E(S)b蕴含θ(a)R∗，∼Vθ(b).类似地，可证aL∗，∼b蕴含θ(a)L∗，∼θ(b).故 θ为允许同态.证毕.

引理 5令 ρ为r-宽大半群(S,E(S))上 的允许同余.则 ((S,E(S))/ρ,E(S)/ρ)是E(S)/ρ上的r-宽大半群.

证明记(T,V)=((S,E(S))/ρ,E(S)/ρ).据引理4，对任意a∈(S，E(S))，存在幂等元e∈La∗，∼∩E(S)，f∈Ra∗，∼∩E(S)，使得aρL∗，∼eρ，aρR∗，∼V fρ.显然eρ,fρ ∈V，且V⊆E(T).这证明了 ((S，E(S))/ρ,E(S)/ρ)为E(S)/ρ上的r-宽大半群.证毕.

对于拟弱适当半群S，如果E(S)是 一个带E，我们用E(e)表 示带E中包含幂等元e的 D-类.

定义 1在拟弱适当半群S上定义关系 δ如下：

定义 2在带E的 D-类上定义一个偏序集如下：

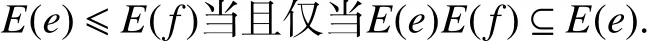
引理 6令S为拟弱适当半群，a,b∈S，aδb且 R∗，∼为左同余.则下列3 款成立：

(ⅰ)E(a+)=E(b+)，E(a∗)=E(b∗)；

(ⅱ)E(a+)aE(a∗)=E(b+)bE(b∗)；

(ⅲ)aδ=E(a+)aE(a∗).

证明(ⅰ)因aδb，则存在e∈E(a+)，f∈E(a∗)，使得b=eaf.显然eb=b.由bR∗，∼b+和 R∗，∼为左同余，得b+R∗，∼eb+.据引理3，知b+Reb+，于是有eb+=b+，从而E(a+)E(b+)⊆E(b+)，故E(b+)≤E(a+).类似地，可证E(b∗)≤E(a∗).这意味着a+b+∈E(b+)，b∗a∗∈E(b∗).又因为

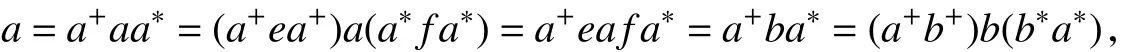
这表明了bδa.显然，(a+b+)a=a.又由aR∗，∼a+和 R∗，∼为左同余，知a+R∗，∼(a+b+)a+.再由引理3，知a+R(a+b+)a+，于是有(a+b+)a+=a+，从而E(b+)E(a+)⊆E(a+)，故E(a+)≤E(b+).类似可证E(a∗)≤E(b∗).这证明了E(a+)=E(b+)，E(a∗)=E(b∗).

c∈E(b+)bE(b∗)g∈E(b+)=E(a+)h∈E(b∗)=E(a∗)

(ⅱ)设，则存在幂等元，，使得

因此，E(b+)bE(b∗)⊆E(a+)aE(a∗).

反之，设d∈E(a+)aE(a∗)，则存在幂等元 λ ∈E(a+)=E(b+)，µ∈E(a∗)=E(b∗)，使得

因此，E(a+)aE(a∗)⊆E(b+)bE(b∗).故E(a+)aE(a∗)=E(b+)bE(b∗).

(ⅲ) 由 δ定义可得(ⅲ)成立.证毕.

引理 7令S为r-宽大半群，E(S)为 正规带，且 R∗,∼为左同余.则下列3 款成立：

(ⅰ)δ为S上的同余关系；

(ⅱ) δ为S上的允许同余；

(ⅲ)S/δ为弱适当半群.

证明 1(ⅰ)显然，δ是自反的.由引理6(ⅰ)的证明，得 δ是对称的.下证 δ是传递的.令a，b，c∈S，使得aδb，bδc.则存在e∈E(a+)，f∈E(a∗)，g∈E(b+)，h∈E(b∗)，使得b=eaf，c=gbh.因此c=geafh，据引理6，知E(a+)=E(b+)=E(c+)，E(a∗)=E(b∗)=E(c∗)，于是有ge∈E(a+)，fh∈E(a∗)，从而aδc.这表明 δ是传递的.因此，δ是S上的等价关系.

要证 δ是S上的同余关系，只需再证 δ是相容的.为此，假设aδb.则存在e∈E(a+)，f∈E(a∗)，使得b=ea f.因此，对于任意c∈S，由E(S)为正规带，得

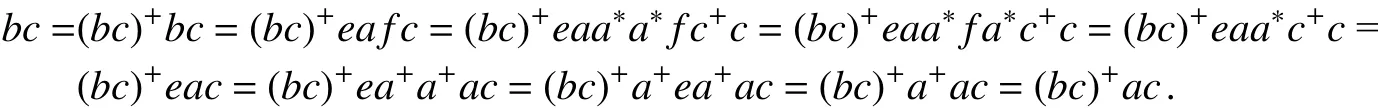
又因为 R∗，∼为 左同余，则 (bc)+R∗，∼(bc)+(ac)+.据引理3，(bc)+R(bc)+(ac)+.因此，(bc)+=((bc)+(ac)+)(bc)+且(bc)+(ac)+=(bc)+((bc)+(ac)+)，故E((bc)+)≤E((bc)+(ac)+)且E((bc)+(ac)+)≤E((bc)+).这证明了E((bc)+)=E((bc)+(ac)+).因为 ((bc)+(ac)+)(ac)+=(bc)+(ac)+，则E((bc)+(ac)+)≤E((ac)+)，因此，E((bc)+)≤E((ac)+).根据 δ的对称性，类似地，可证ac=(ac)+bc.因此，E((ac)+)≤E((bc)+)，故E((ac)+)=E((bc)+).又据bc=(bc)+ac=(bc)+ac(ac)∗，其中 (bc)+∈E((bc)+)=E((ac)+)，(ac)∗∈E((ac)∗).因此，acδbc，δ是右相容的.类似地，可证 δ是左相容的.这证明了 δ 是S上的同余关系.

(ⅱ)令aL∗，∼b.设x，y∈S1，(ax)δ=(ay)δ，则存在m∈E((ax)+)，n∈E((ax)∗)，使得ay=maxn.又因为E(S)是正规带，则有

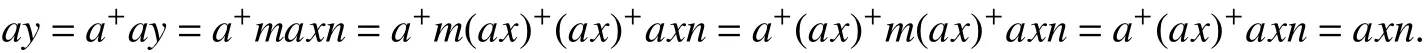
由aL∗，∼b，得by=bxn=(bx)+bxn.又因为aL∗，∼b且 L∗，∼为 右同余，则axL∗，∼bx，从而有 (ax)∗L∗，∼(bx)∗.据引理3，得 (ax)∗L(bx)∗，因此 (ax)∗=(ax)∗(bx)∗且 (bx)∗=(bx)∗(ax)∗.故E((ax)∗)≤E((bx)∗)且E((bx)∗)≤E((ax)∗).这证明E((ax)∗)=E((bx)∗).又据by=(bx)+bxn，其中n∈E((ax)∗)=E((bx)∗)，(bx)+∈E((bx)+)，因此，(bx)δ=(by)δ.类似可证 (bx)δ=(by)δ蕴含 (ax)δ=(ay)δ.这证明了aδL∗，∼bδ.

令aR∗，∼b.设e∈E(S)，eδaδ=aδ，则存在p∈E((ea)+)，q∈E((ea)∗)，使得a=peaq.显然，aq=a.因此aqR∗，∼b.又 由aq=a=peaq，得b=peb=peb(eb)∗.因aR∗，∼b且 R∗，∼为左同余，则eaR∗，∼eb.从而 (ea)+R∗，∼(eb)+.据引理3，(ea)+R(eb)+，因此，(ea)+=(eb)+(ea)+且 (eb)+=(ea)+(eb)+.故E((ea)+)≤E((eb)+)且E((eb)+)≤E((ea)+)，这 证明 了E((ea)+)=E((eb)+).又据b=peb(eb)∗，其中p∈E((ea)+)=E((eb)+)，(eb)∗∈E((eb)∗)，因此，eδbδ=bδ.类似可证eδbδ=bδ 蕴含eδaδ=aδ.这就证明了aδR∗，∼Vbδ，V=E(S)/δ.因此，δ 为S上的允许同余.

(ⅲ)显然S/δ是 L∗，∼-富足和 R∗，∼-富足的，则S/δ为r-宽大半群.

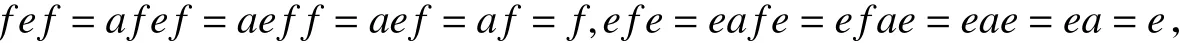
下证E(S/δ)为 半格.因为S为r-宽大半群，则对任意a∈E(S)，存在e，f∈E(S)，使得aL∗，∼e，aR∗，∼f.据引理3，aLe，aRf.因此a=ae且e=ea，a=fa且f=af，因为E(S)为正规带，则进而fLef，eRef.又因为e fR∗，∼(e f)+和e fL∗，∼(e f)∗，则e fR(ef)+，e fL(ef)∗.从而fLe fR(e f)+，eRefL(ef)∗，因此fD(ef)+，eD(ef)∗，故f∈E((ef)+)，e∈E((ef)∗).又因为E(S)为 正规带，则fe=f fee=fefe，其中f∈E((ef)+)，e∈E((ef)∗)，故有e fδfe，从而eδfδ=fδeδ.这证明了E(S/δ)为 半格.因此，S/δ为弱适当半群.证毕.

引理8[11]令S为弱适当半群，E(S)为S的幂等元集，且a，b∈S.则下列5 款成立：

(ⅰ)aL∗，∼b当且仅当a∗=b∗；aR∗,∼b当且仅当a+=b+；

(ⅱ) 一般地，(ab)∗=(a∗b)∗，但 (ab)+≠(ab+)+；

(ⅲ) 若 R∗，∼为 左同余，则 (ab)+=(ab+)+；

(ⅳ) 对任意e∈E(S),(ae)∗=a∗e；若 R∗，∼是 左同余，则 (ea)+=ea+；

(ⅴ) 若 R∗，∼为 左同余，则 (ab)+≤a+,(ab)∗≤b∗，其中 ≤是E(S)上的自然偏序.

2 拟织积结构

令半群T为弱适当半群，Y为其幂等元集的半格.令为一左正规带关于左零带Lα的强半格，为 一右正规带关于右零带Rα的强半格.设集合QS=QS(L，R，T；Y)={(e，a，f)∈L×T×R：a∈T，e∈La+，f∈Ra∗}.定义QS上的乘法如下：

其中ab为a和b在T上的积.据引理8(ⅴ)，知 (ab)+≤a+，(abc)+≤(ab)+.因 此，a+≥(ab)+≥(abc)+，故φa+,(ab)+φ(ab)+,(abc)+=φa+,(abc)+.对任意 (e,a,f),(u,b,v),(i,c,j)∈QS，有

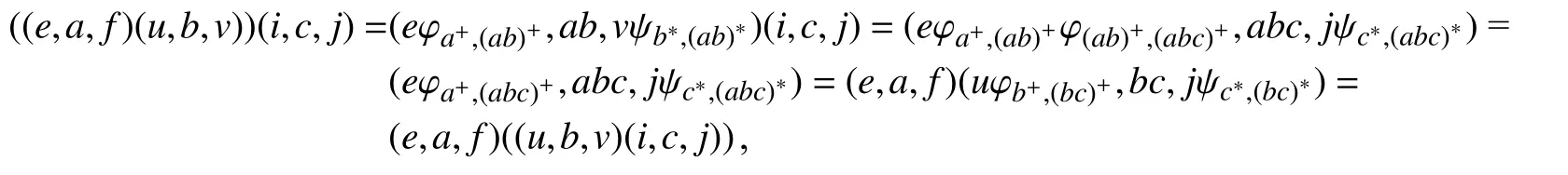
因此，QS关于上述运算构成半群.我们把QS称为左正规带L，右正规带R和弱适当半群T关于半格Y的拟织积.

引理 9令QS为左正规带L，右正规带R和弱适当半群T关于半格Y的拟织积，(e,a,f)，(u,b,v)∈QS，且R∗，∼为左同余.则下列4 款成立:

(ⅰ) (e,a,f)∈E(QS)当且仅当a∈E(T)；

(ⅱ) (e,a,f)L∗，∼(a∗,a∗,f),(e,a,f)R∗，∼(e,a+,a+)；

(ⅲ) (e,a,f)L∗，∼(u,b,v)当且仅当aL∗，∼(T)b且f=v；

(ⅳ) (e,a,f)R∗，∼(u,b,v)当且仅当aR∗，∼(T)b且e=u.

证明(ⅰ)设 (e,a,f)∈E(QS).则 (e,a,f)=(e,a,f)(e,a,f)=(eφa+,(a2)+，a2,fψa∗,(a2)∗).因此a2=a，即a∈E(T).反之，假设a∈E(T)，则a2=a，从而

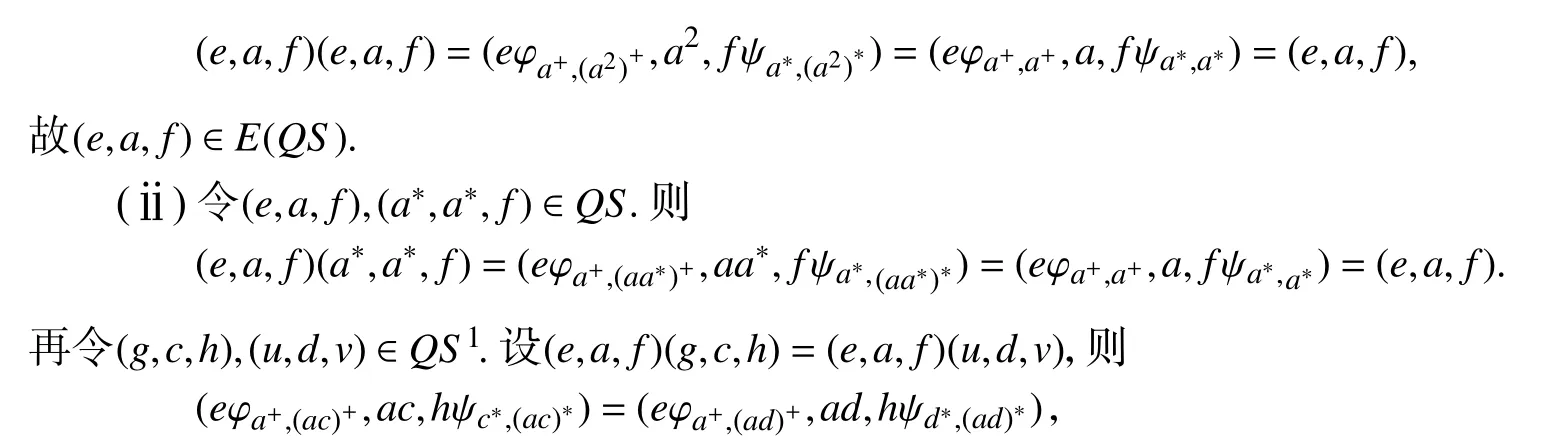
从而有ac=ad且hψc∗，(ac)∗=hψd∗，(ad)∗.因为aL∗，∼a∗，则a∗c=a∗d.又因为L∗，∼为右同余，则acL∗，∼a∗c，adL∗，∼a∗d，从而 (ac)∗L∗，∼(a∗c)∗，(ad)∗L∗，∼(a∗d)∗.据引理8(ⅰ)，知 (ac)∗=(a∗c)∗，(ad)∗=(a∗d)∗，故有

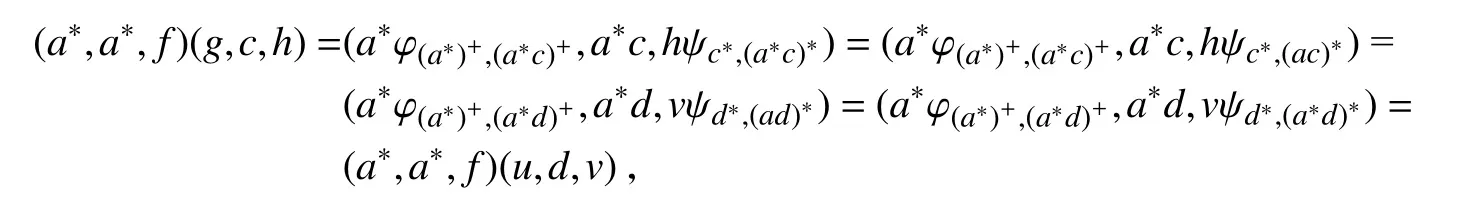
因此，(e,a,f)L∗，∼(a∗,a∗,f).

下证 (e,a,f)R∗，∼(e,a+,a+).令 (e,a,f),(e,a+,a+)∈QS，则

再令 (g,c,h)∈E(QS)，则c∈E(T).假设 (g,c,h)(e,a,f)=(e,a,f)，则

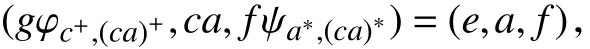
从而ca=a且gφc+,(ca)+=e.因为aR∗,∼a+，则 (ca)+R∗,∼a+，据引理8，知a+=(ca)+=(ca+)+=ca+.故

因此，(e,a,f)R∗，∼(e,a+,a+).

(ⅲ) 由(ⅱ)，得 (e,a,f)L∗，∼(a∗,a∗,f),(u,b,v)L∗，∼(b∗,b∗,v).因为a∗,b∗∈E(T)，且T为弱适当半群，则a∗b∗=b∗a∗.又由(ⅰ)，得 (a∗,a∗,f),(b∗,b∗,v)∈E(QS).据引理3，有

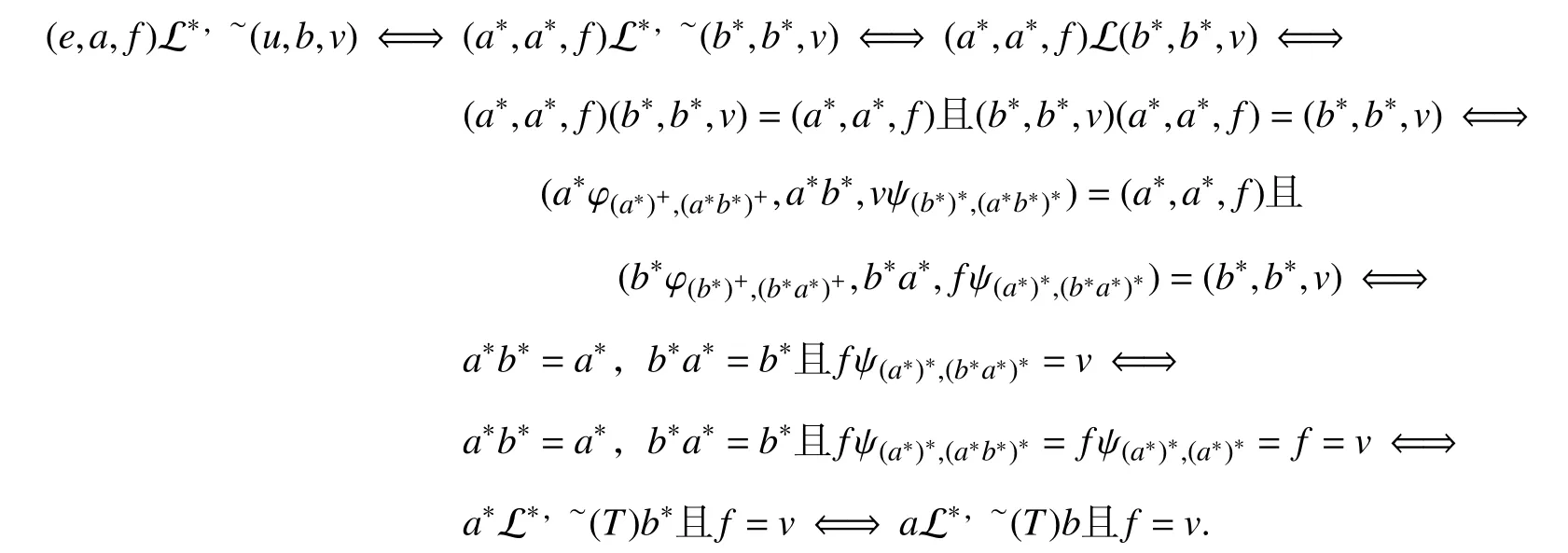
类似地，可证(ⅳ)成立.证毕.

定理 1半群QS=QS(L,R,T;Y)是幂等元集为正规带的r-宽大半群.

证 明据引理9，对任意 (e,a,f)∈QS，有 (e,a,f)L∗，∼(a∗,a∗，f)，(e,a,f)R∗，∼(e,a+,a+)，其中(a∗,a∗,f),(e,a+,a+)∈E(QS).因此，QS为r-宽大半群.

下证E(QS)为正规带.令 (e,a,f)，(u,b,v)，(i,c,j)，(s,d,t)∈E(QS).由引理9(ⅰ)，得a,b,c,d∈E(T).因T为弱适当半群，则由幂等元可交换得abcd=acbd.从而有

因此，E(QS)为正规带.故QS=QS(L,R,T;Y)是幂等元集为正规带的r-宽大半群.证毕.

定理 2令QS=QS(L,R,T;Y)，且R∗,∼为左同余.则QS/δ ≅T.

证明构造映射ϕ:QS/δ →T，(e,a,f)δa.令a,b∈T，(e,a,f)，(u,b,v)∈QS.设 (e,a,f)δ=(u,b,v)δ，则存在(i,c,j)∈E((u,b,v)+)，(s,d,t)∈E((u,b,v)∗)，使得 (e,a,f)=(i,c,j)(u,b,v)(s,d,t).据引理9(ⅰ)，知c,d∈E(T).

下面证明 (e,a,f)R∗，∼(i,c,j).显然，(i,c,j)(e,a,f)=(e,a,f).假设对任意 (x,g,y)∈E(QS)，有(x,g,y)(e,a,f)=(e,a,f).则我们可以得到(1)式

因为 (s,d,t)∈E((u,b,v)∗)，则存在(λ,k,µ)∈E(QS)，使得 (s,d,t)R(λ,k,µ)L(u,b,v)∗，故(λ,k,µ)=(s,d,t)(λ,k,µ).再将(1) 式的两边同时右乘(λ,k,µ)后可得(2)式

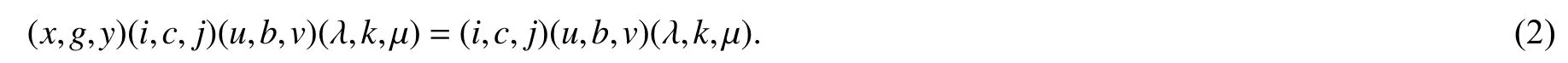
又因为(λ,k,µ)L(u,b,v)∗，(u,b,v)L∗，∼(u,b,v)∗，故

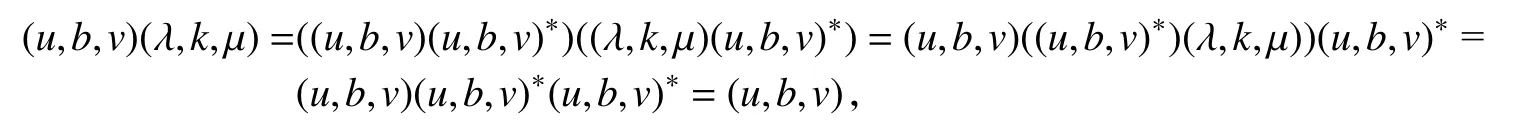
从而(2) 式可简化为 (x,g,y)(i,c,j)(u,b,v)=(i,c,j)(u,b,v).因为R∗，∼为左同余，且 (u,b,v)R∗，∼(u,b,v)+，则(i,c,j)(u,b,v)R∗，∼(i,c,j)(u,b,v)+.据R∗，∼的定义，对任意 (x,g,y)∈E(QS)，当(x,g,y)(i,c,j)(u,b,v)=(i,c,j)(u,b,v)时，(x,g,y)(i,c,j)(u,b,v)+=(i,c,j)(u,b,v)+成立.从而 (x,g,y)(i,c,j)(u,b,v)+(i,c,j)=(i,c,j)(u,b,v)+(i,c,j)，即(x,g,y)(i,c,j)=(i,c,j).这证明了 (e,a,f)R∗，∼(i,c,j).

下证 (e,a,f)L∗，∼(s,d,t).显然 (e,a,f)(s,d,t)=(e,a,f).假设对任意 (x,g,y)，(λ,k,µ)∈QS1，有(e,a,f)(x,g,y)=(e,a,f)(λ,k,µ)，则我们可以得到(3)式

因为 (i,c,j)∈E((u,b,v)+)，则存在 (p,h,q)∈E(QS)，使得 (i,c,j)L(p,h,q)R(u,b,v)+，故 (p,h,q)=(p,h,q)(i,c,j).再将(3)式的两边同时左乘 (p,h,q)后可得(4) 式：

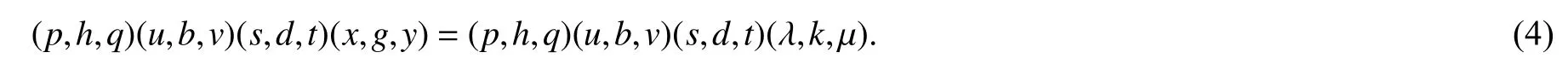
又因为 (p,h,q)R(u,b,v)+，(u,b,v)R∗，∼(u,b,v)+，则

从而(4) 式可简化为 (u,b,v)(s,d,t)(x,g,y)=(u,b,v)(s,d,t)(λ,k,µ).因为L∗，∼为右同余，且 (u,b,v)L∗，∼(u,b,v)∗，则(u,b,v)(s,d,t)L∗，∼(u,b,v)∗(s,d,t).又据L∗，∼的定义，得 (u,b,v)∗(s,d,t)(x,g,y)=(u,b,v)∗(s,d,t)(λ,k,µ).再两边同时左乘 (s,d,t)可得 (s,d,t)(u,b,v)∗(s,d,t)(x,g,y)=(s,d,t)(u,b,v)∗(s,d,t)(λ,k,µ)，即 (s,d,t)(x,g,y)=(s,d,t)(λ,k,µ).这证明了 (e,a,f)L∗，∼(s,d,t).

据引理9，知aR∗，∼c，aL∗，∼d，从而a+R∗，∼c，a∗L∗，∼d.又据引理8(ⅰ)，a+=c，a∗=d，因此，a=cbd=a+ba∗.类似地有b=b+ab∗成立.因T为弱适当半群，则由幂等元交换得

从而 (e,b+,v) ∈E((u,b,v)+)，(u,b∗,f)∈E((u,b,v)∗)，因此 (e,a,f)δ=(u,b,v)δ.综上可知QS/δ ≅T.证毕.

定理 3令S是幂等元集为正规带的r-宽大半群，且R∗，∼为左同余.则，其中 LE,RE和 DE为E上的格林关系.

证明假设S是幂等元集为正规带的r-宽大半群.由E(S)为 正规带，知E(S)为矩形带Eα的强半格S(Y;Eα;ϕα,β)，这里Eα是E的 D -类.因此Y≅E/DE.令Eα为 左零带Lα与右零带Rα的直积，即Eα=Lα×Rα.据文献[10]的推论4.4.3，半群同态α,β:Eα→Eβ(α ≥β)决定了同态映射φα,β:Lα→Lβ和ψα,β:Rα→Rβ，使得对任意(lα，rα)∈Eα，有 (lα，rα)ϕα,β=(lαφα,β，rαψα,β).同时L和R分 别为左正规带和右正规带，显然L和R关于半格Y的织积为E，因此L≅E/RE，R≅E/LE.因为E(S)为 正规带，据引理7，知 δ为 允许同余且S/δ为弱适当半群.注意到 δ对E的限制 δ|E为DE，因此，E(S/δ)≅Y.

为简单起见，我们分别用L，R和Y来表示E/RE,E/LE和E/DE.构造映射

由S/δ为 弱适当半群和引理8，得 δ((ab)+)=δ(a+)δ((ab)+)=δ((ab)+)δ(a+)，故 δ(a+)≥δ((ab)+).因此，由 RE是E上的同余，得

最后，证明θ 是满射.令(e,x,f)∈QS(L,R,S/δ;Y)，则存在a∈S，使得令幂等元g,h∈E(S)，则，于是有δ(g)=δ(a+)=(δ(a))+,δ (h)=δ(a∗)=(δ(a))∗，从 而δ(g)δ(a)δ(h)=(δ(a))+δ(a)(δ(a))∗=δ(a).因为 θ是同态映射，则