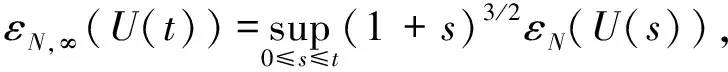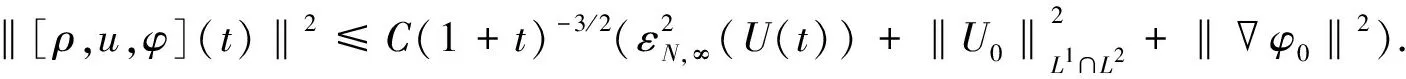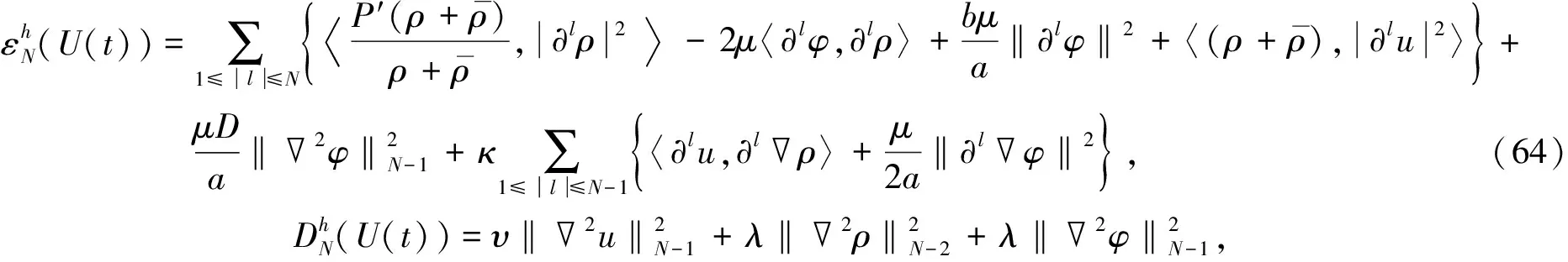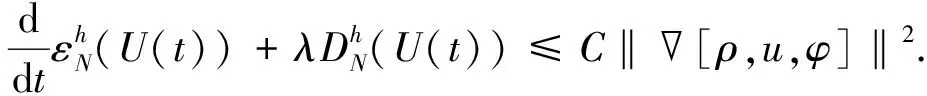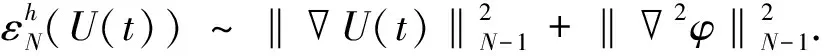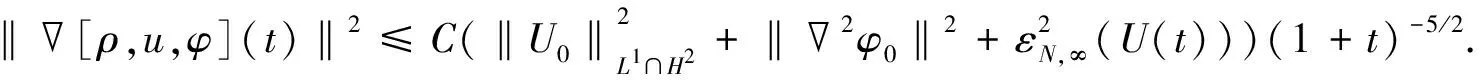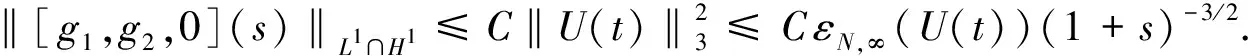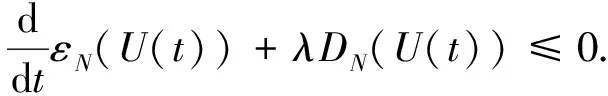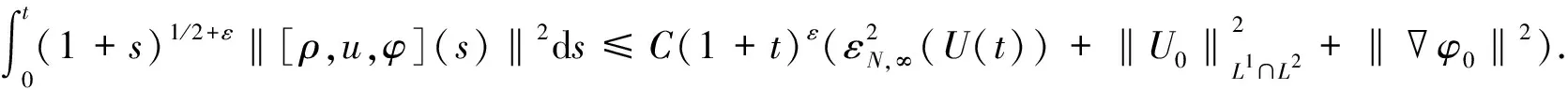黏性血管生成模型解的全局存在性和大时间行为
伍小莉, 刘青青
(华南理工大学 数学学院, 广州 510641)
1 引言与主要结果
血管生成(Vasculogenesis)是血管网络形成的前提, 其反应机制非常复杂. 为描述血管生成的过程, Gamba等[1]提出了如下带黏性的血管生成模型:

(1)
其中: 未知函数n=n(t,x)>0和u=u(t,x)∈3分别表示内皮细胞的密度和速度,c=c(t,x)表示化学引诱剂的浓度, 并且t>0,x∈3; 正常数D,a和b分别表示扩散系数、 释放率和化学引诱剂降解时间的倒数; 正常数μ和υ分别表示细胞对化学信号的反映强度和黏性系数;P表示压力, 是一个仅依赖于密度的光滑函数, 并且对∀n>0, 有P′(n)>0.方程的初始条件为
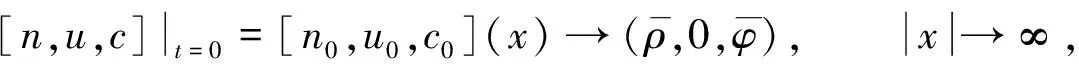
(2)
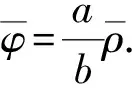
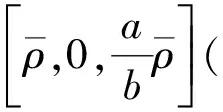
带黏性的血管生成模型(1)可视为带趋化外力的Navier-Stokes方程耦合一个抛物方程, 也可视为将Poisson方程替换为抛物方程的Navier-Stokes-Poisson方程. 因此, 研究Navier-Stokes方程以及Navier-Stokes-Poisson方程的相关结果对该问题的研究具有启发意义. 文献[7-9]研究了Navier-Stokes方程常状态附近的扰动理论; 文献[10]给出了研究双曲抛物型耦合方程解的最优衰减率方法; 当考虑势外力时, 文献[11]和文献[12]分别研究了等熵和非等熵Navier-Stokes方程非平凡Profile附近解的最优衰减率问题; 文献[13-16]研究了Navier-Stokes方程的Cauchy问题、 半空间问题、 有界域问题不同渐近态附近解的稳定性以及衰减率等; 文献[17-19]研究了Navier-Stokes-Poisson方程解的全局存在性和衰减估计.
与文献[18]中的Navier-Stokes-Poisson方程:
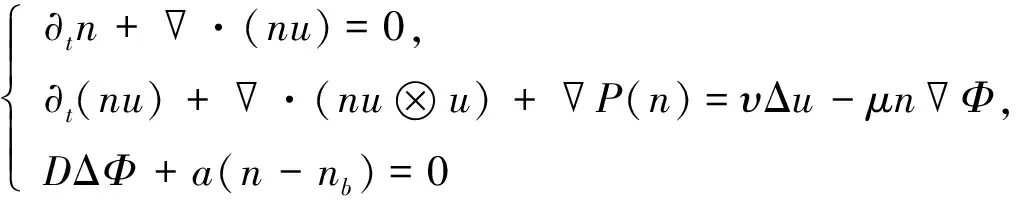
(3)
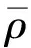
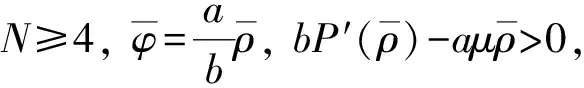
则存在C0>0, 使得Cauchy问题(1)-(2)存在唯一的全局解, 满足
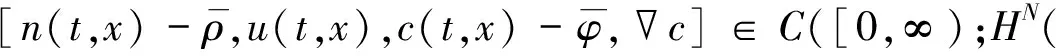
且
此外, 若还存在δ1>0, 使得
则存在常数C1>0, 使得对∀t≥0, 有
本文首先在常平衡态附近做扰动, 重述Cauchy问题(1)-(2), 并用Fourier能量方法给出相应线性齐次系统解的衰减估计; 其次用能量方法证明问题(1)-(2)解的全局存在性; 最后利用时间加权能量方法给出方程解在常平衡态附近的衰减率.
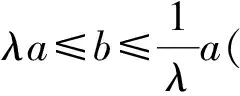
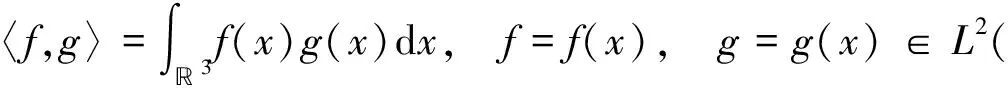
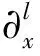

其中i为虚数单位.
2 齐次线性系统解的Lp-Lq衰减估计
2.1 用扰动函数重述问题
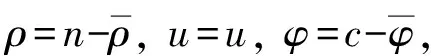
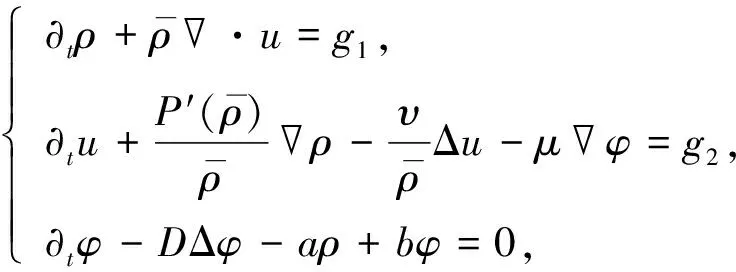
(4)
初始条件为
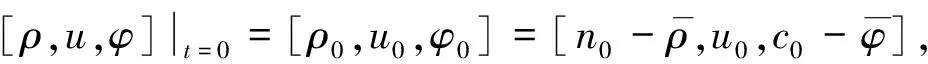
(5)
其中g1,g2为
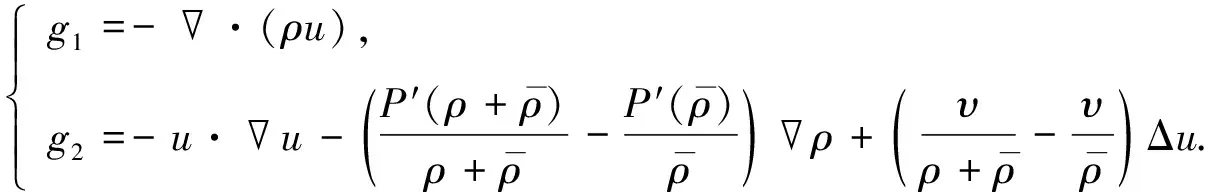
(6)
2.2 Fourier空间中线性方程的能量估计
下面考虑Cauchy问题(4)-(5)相应线性齐次系统解的衰减估计. 为此, 首先给出问题(4)-(5)相应的线性齐次方程组:

(7)
初始条件为
[ρ,u,φ]|t=0=[ρ0,u0,φ0]→[0,0,0], |x|→∞.
(8)
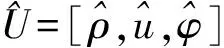
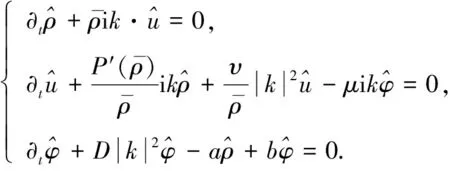
(9)
初始条件为

(10)
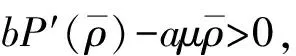
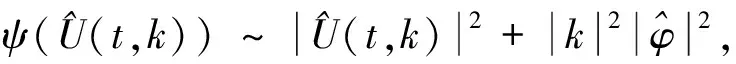
(11)
且存在λ>0, 使得对∀t>0,k∈3, 有

(12)
证明: 为使运算结果更简洁, 用记号(a|b)表示a点乘b的共轭, 其中a,b是两个复数或者向量.通过直接运算, 易得

(13)

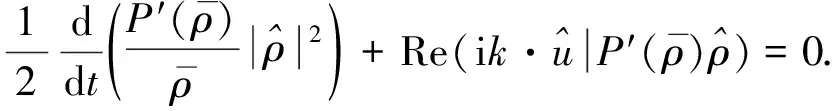
(14)

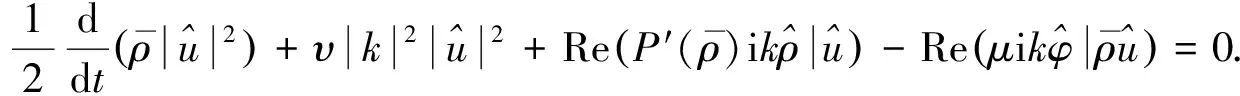
(15)
将式(14)+式(15), 利用方程(9)中第一式, 且注意到
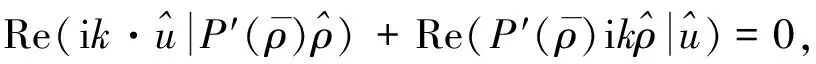
有
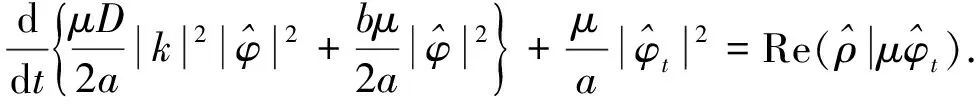
(17)
式(17)+式(16), 有
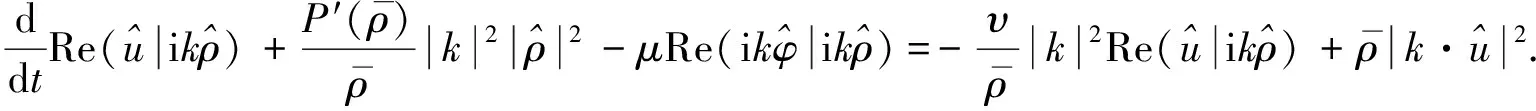
(19)
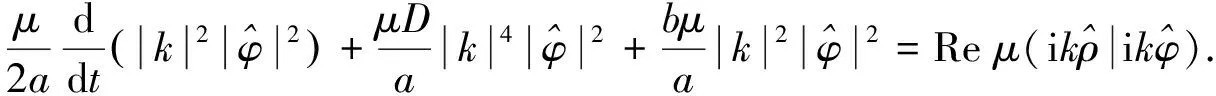
(20)
式(19)+式(20), 有
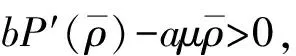
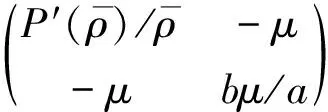
(22)
是正定矩阵.即存在常数C2>0, 使得

(23)
将式(23)与式(21)结合, 再利用Cauchy-Schwarz不等式, 易得
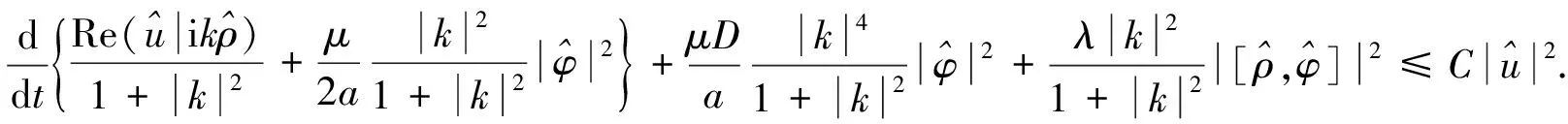
(25)
定义
其中0<κ≪1待定.由于矩阵(22)是正定矩阵, 所以存在另一个常数C3>0, 使得

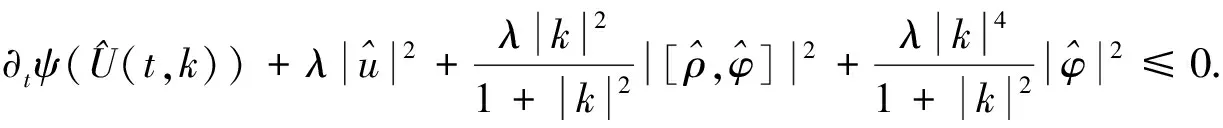
(27)
注意到

(28)
结合不等式(27),(28), 易知式(12)成立.证毕.
由定理2直接可得以下两个推论.
推论1∀t≥0,x∈3, 令U(t,x)是方程组(7)-(8)的解, 则存在λ>0,C>0, 使得对∀t≥0,k∈3, 有
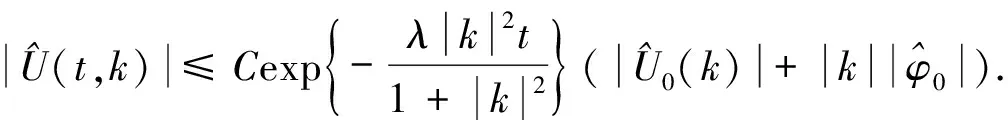
(29)
由式(29)可得Cauchy问题(7)-(8)解的Lp-Lq时间衰减估计.形式上, 方程组(7)-(8)的解可记为
U(t)=[ρ,u,φ]=etLU0,
其中etL(t≥0)是线性化方程的解算子.
推论2[20]令1≤p,r≤2≤q≤∞,l≥0,m≥0是整数.定义
其中[·]-表示取整函数, 则对∀t≥0, 存在C=C(m,p,r,q,l), 使得
3 非线性系统解的渐近行为
3.1 解的全局存在性
仍用记号U=[ρ,u,φ]表示非线性系统(4)-(6)的解.下面总假设N≥4.为使结论更简明, 定义能量泛函εN(U(t))和耗散DN(U(t))分别为
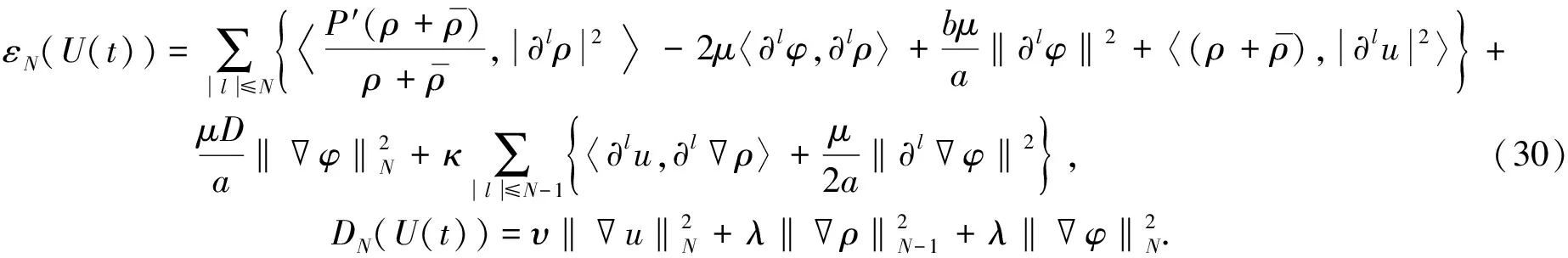
(31)
定理3若εN(U0)>0充分小, 则Cauchy问题(4)-(6)存在唯一全局解U=[ρ,u,φ], 且满足
U∈C([0,∞);HN(3)),φ∈C([0,∞);HN(3)).
此外, 存在如式(30)所示的εN(U(t))满足对∀t≥0, 有

由文献[21]知, 要证明定理3成立, 只需证明下述先验估计成立.
引理1假设存在T>0, 使得U=[ρ,u,φ]∈C([0,T);HN(3))是Cauchy问题(4)-(6)在[0,T)上的解, 满足则存在如式(30)所定义的εN(U(t)), 使得对∀0≤t (32) 证明: 证明分三步. 1) 证明 成立. 为证明式(33)成立, 将式(4)改写为如下形式: (34) (37) 将式(36),(37)代回式(35), 有 (41) 将式(40),(41)代回式(39), 有 将式(43)中ρt用方程(34)中第一式代替, 并改写式(43)的最后一项, 有 将式(44)代入式(43), 有 将式(38),(42),(45)相加, 有 其中 (48) 结合估计(47),(48), 并对式(46)两边关于0≤|l|≤N累加, 易得式(33)成立. 2) 证明 成立. 为证明式(49)成立, 先考虑方程(4)-(6).首先, 令0≤|l|≤N-1, 将∂l先作用于方程(4)中第二式, 然后乘以∂lρ, 最后将所得结果关于x在3上积分.利用分部积分并用方程(4)中第一式代替∂tρ, 有 (51) 将式(50)和式(51)相加, 有 因为矩阵(22)是正定矩阵, 所以存在常数C4>0, 使得 最后, 对式(52)利用Cauchy-Schwarz不等式, 有 其中g1,g2的定义见式(6).利用Sobolev不等式和Cauchy-Schwarz不等式及Hölder不等式, 有 (54) 将式(54)代入式(53), 并把所得结果两边关于|l|≤N-1求和, 易知式(49)成立. 3) 证明定理3成立. 令0<κ≪1为式(30)中充分小的待定常数, 令2×式(33)+κ×式(49).注意以下3个事实: (55) ② 由式(22)是正定矩阵, 所以存在常数C5,C6>0, 使得 结合式(30),(31)中εN(U(t))和DN(U(t))定义, 易见存在λ>0,C>0, 使得 ∂tεN(U(t))+λDN(U(t))≤C[εN(U(t))1/2+εN(U(t))]DN(U(t)) 成立, 即式(32)成立.因此引理1成立.再结合局部存在性理论和连续性技巧可知定理3成立. 下面主要说明当初始条件U0=[ρ0,u0,φ0]具有一定的正则性和可积性时, 定理3中的解U=[ρ,u,φ]具有一定的时间衰减.为使结论更简洁, 记 τm(U0)=‖U0‖m+‖φ0‖m+‖U0‖L1, (57) 其中m≥0是整数. 先对‖[ρ,u,φ](t)‖2进行估计.记 (58) 则可得如下引理. 引理2对∀t≥0, 有 (59) 证明: 由Duhamel原理, 初始条件为U0=[ρ0,u0,φ0]的Cauchy问题(4)-(6)的解U=[ρ,u,φ]形式上可以写为 (60) 其中etL(t≥0)是线性化方程的解算子,g1,g2如式(6)所示.结合推论2, 当取m=0,q=r=2,p=1时, 有 (61) 结合g1,g2的定义(式(6))及εN,∞(·)的定义(式(58)), 通过直接计算可知, 对任意的0≤s≤t, 有 ‖[g1,g2](s)‖L1∩L2≤CεN(U(s))≤(1+s)-3/2εN,∞(U(t)). (62) 把估计式(62)代入式(61)中最后一项, 有 ‖[ρ,u,φ](t)‖≤C(1+t)-3/4(‖U0‖L1∩L2+‖φ0‖+εN,∞(U(t))), (63) 对式(63)两边平方即可得式(59)成立.证毕. 记 (65) 其中0<κ≪1是充分小的待定常数. (66) 证明: 类似于引理1中式(33),(49)的证明过程, 求和时只要取1≤|l|≤N的项, 即有 令0<κ≪1为式(64)中充分小的待定常数, 令2×式(67)+κ×式(68).基于式(55),(56)和0<κ≪1充分小, 有 易知式(66)成立.证毕. 引理4假设定理3的条件成立, 则对∀t≥0, 有 (69) 证明: 在推论2中令m=1,q=r=2,p=1, 结合式(60), 有 其中g1,g2的定义见式(6).用Minkowski不等式、 Hölder不等式以及定义式(58), 易证 (71) 把估计式(71)代入式(70)的最后一项, 可得 ‖[ρ,u,φ](t)‖≤CεN,∞(U(t)))(1+t)-5/4, 表明式(69)成立. 定理4假设定理3的条件成立, 且τN(U0)>0充分小, 则对∀t≥0, 解U=[ρ,u,φ]满足 ‖U(t)‖N+‖φ‖N≤CτN(U0)(1+t)-3/4, (72) (73) 证明: 首先, 证明带时间权重的εN(U(t))有如下估计.当1 (74) 由引理1知, 对∀t≥0, 有 (75) 下面用迭代法证明式(74)成立.对∀l≥0, 在不等式(75)两边同时乘以(1+t)l, 并将所得结果关于时间t在[0,t]上积分, 有 (76) 由εN(U(t))和DN(U(t))的定义易知 εN(U(t))≤C(DN(U(t))+‖[ρ,u,φ](t)‖2). (77) 结合式(76),(77), 有 类似上述过程, 用l-1代替l, 有 当1 由定理3, 有 (81) 结合式(80),(81), 当1 由式(78),(82)知式(74)成立. 其次, 通过式(74)和引理2说明由式(58)所定义的εN,∞(U(t))关于时间一致有界, 且 (83) 从而说明式(72)成立(τN(·)如式(57)所示).下面证明式(83)成立.在式(74)中, 取l=3/2+ε(其中ε>0充分小), 有 结合式(59), 可对式(84)中最后一项进行估计.注意到εN,∞(U(t))关于时间t单调不减, 有 (85) 由式(84),(85), 有 这表明 所以有 又由条件τN(U0)>0充分小, 进一步知式(83)成立.再结合εN(·)和τN(·)的定义式(30)和(57), 易知对∀t≥0, 有 ‖U(t)‖N+‖φ‖N≤CεN(U(t))1/2≤CτN(U0)(1+t)-3/4, (86) 从而式(72)成立. (87) 将式(87)两边关于t在[0,t]上积分, 有 (88) 再结合引理4, 利用式(69),(88)以及式(83)易证如下结论成立: 从而式(73)成立.进而可得定理1中方程解的衰减估计.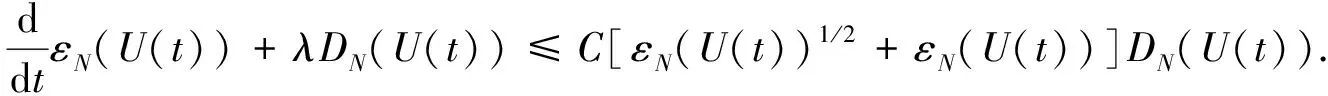
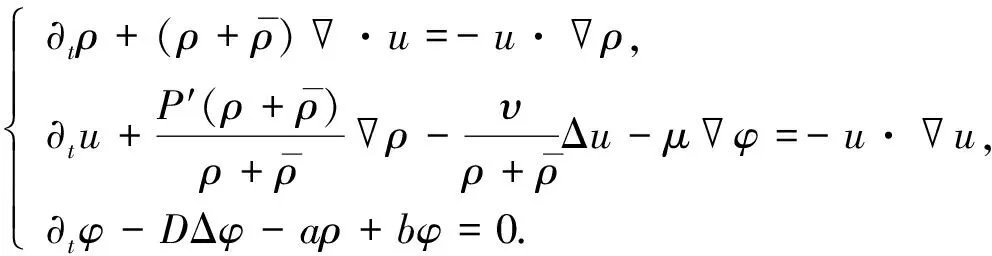
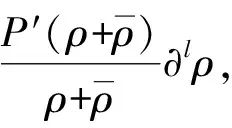


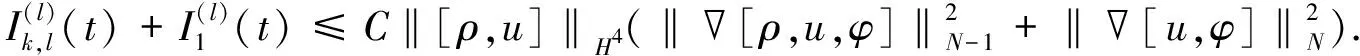
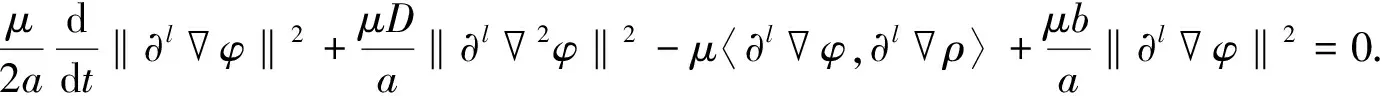
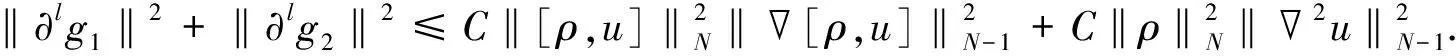
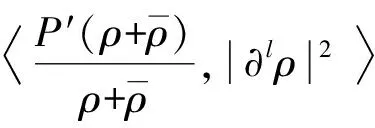
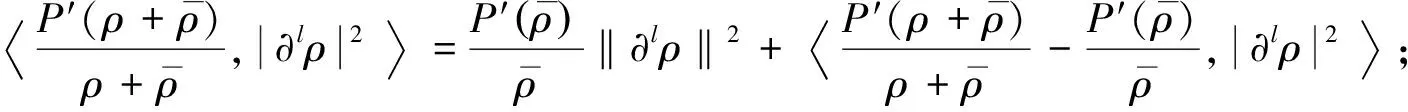
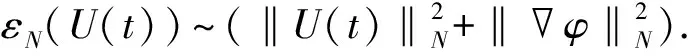
3.2 解的渐近行为