图变换及其在图的最小无符号拉普拉斯特征值的应用
冯小芸, 陈 旭, 王国平
(新疆师范大学数学科学学院,乌鲁木齐 830017)
0 引言
连通图的最小无符号拉普拉斯特征值已经被广泛研究。Cardoso 等[1]给出了所有非二部图的连通图中最小无符号拉普拉斯特征值是最小的唯一图。Guo 等[2]给出图的最小无符号拉普拉斯特征值的下界。Guo 和Zhang[3]确定了给定最大度的所有非二部图的连通图中最小无符号拉普拉斯特征值是最小的唯一图。Fan 等[4]确定了带有悬挂点的所有非二部图的连通图中最小无符号拉普拉斯特征值分别是最大和最小的唯一图。Guo 等[5]确定了所有单圈图中最小无符号拉普拉斯特征值是最小的唯一图。Wang 和Fan[6]确定了在一类给定非二部图作为诱导子图且有固定阶的连通图中最小无符号拉普拉斯特征值是最小的唯一图。Yu 等[7]确定了所有非二部图的连通双圈图中最小无符号拉普拉斯特征值是最小的唯一图。Yu 等[8]分别确定了给定匹配数和边覆盖数的所有非二部图的连通图中最小无符号拉普拉斯特征值是最小的唯一图。Wen 等[9]分别给出了带有稳定数和覆盖数的所有非二部图中最小无符号拉普拉斯特征值是最小的唯一图。
设G= (V(G),E(G))是一个连通简单图,可定义G的补图Gc= (V(Gc),E(Gc)),其中V(Gc)=V(G)和E(Gc)={xy:x,y ∈V(G),xy/∈E(G)}。若|E(G)|=|V(G)|+1,则称G是一个双圈图。我们定义K1,n−1是带有n个点的星图,若K1,n−1+ 2e是从K1,n−1中连接两对不同的悬挂点对而得到的图,由于K1,n−1+2e的补图(K1,n−1+2e)c含有一个孤立点,所以(K1,n−1+2e)c不连通。显然,不少于12 个点的双圈图的补图是非二部图,所以我们仅考虑不少于12 个点的除了K1,n−1+2e(n ≥12)之外的双圈图的补图。
Li 和Wang[10]确定除星图K1,n−1的所有树的补图中最小无符号拉普拉斯特征值是最小的唯一图。Yu 等[11]确定了除图K1,n−1+e的所有单圈图的补图中最小无符号拉普拉斯特征值是最小的唯一图。本文中,我们给出两种图变换,并且应用它们确定了带有n ≥12 个点除了K1,n−1+2e的所有双圈图的补图中最小无符号拉普拉斯特征值取最小的唯一图。
1 主要结论
假设G是点集为V(G) ={v1,v2,···,vn}的图,下文我们将λn(G)记为λ(G)。令X=(X1,X2,···,Xn)T是一个单位向量,其中Xi=X(vi)(1≤i ≤n),这样有
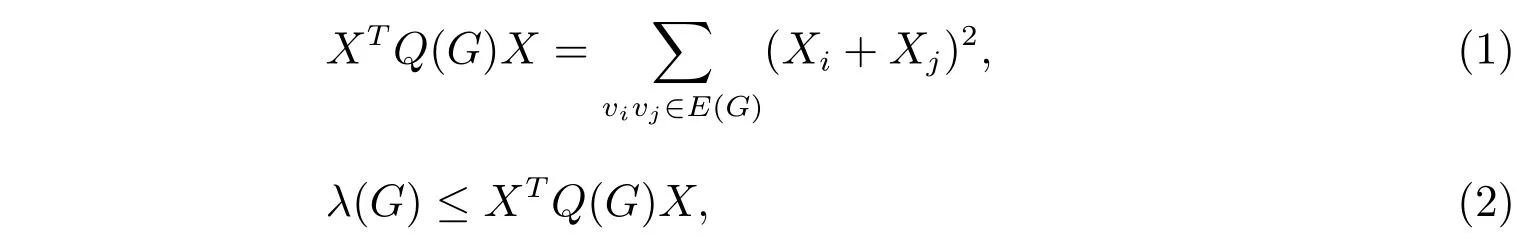
(2)式中的等号成立,当且仅当X是Q(G)的关于特征值λ(G)的特征向量。
本文将带有n个点的图的点集记为{v1,v2,···,vn},令X= (X1,X2,···,Xn)T是一个单位向量,其中Xi=X(vi)(1≤i ≤n),且X1≥X2≥···≥0≥···≥Xn。
引理1[10]设X如上所示,其中X1>0 和Xn<0,则对于任意的1≤i,j ≤n,有
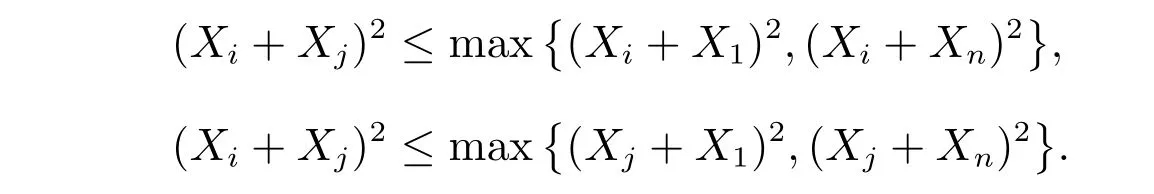
将带有n个点的所有连通双圈图的连通补图的集合记为(n ≥12),那么对于任意G ∈,则有λ(G)>0。
将图G中点vi和点vj之间最短路的长度称为它们之间的距离,记为dG(vi,vj)。
设Gk(p,q)(1≤k ≤12),如图1 所示。
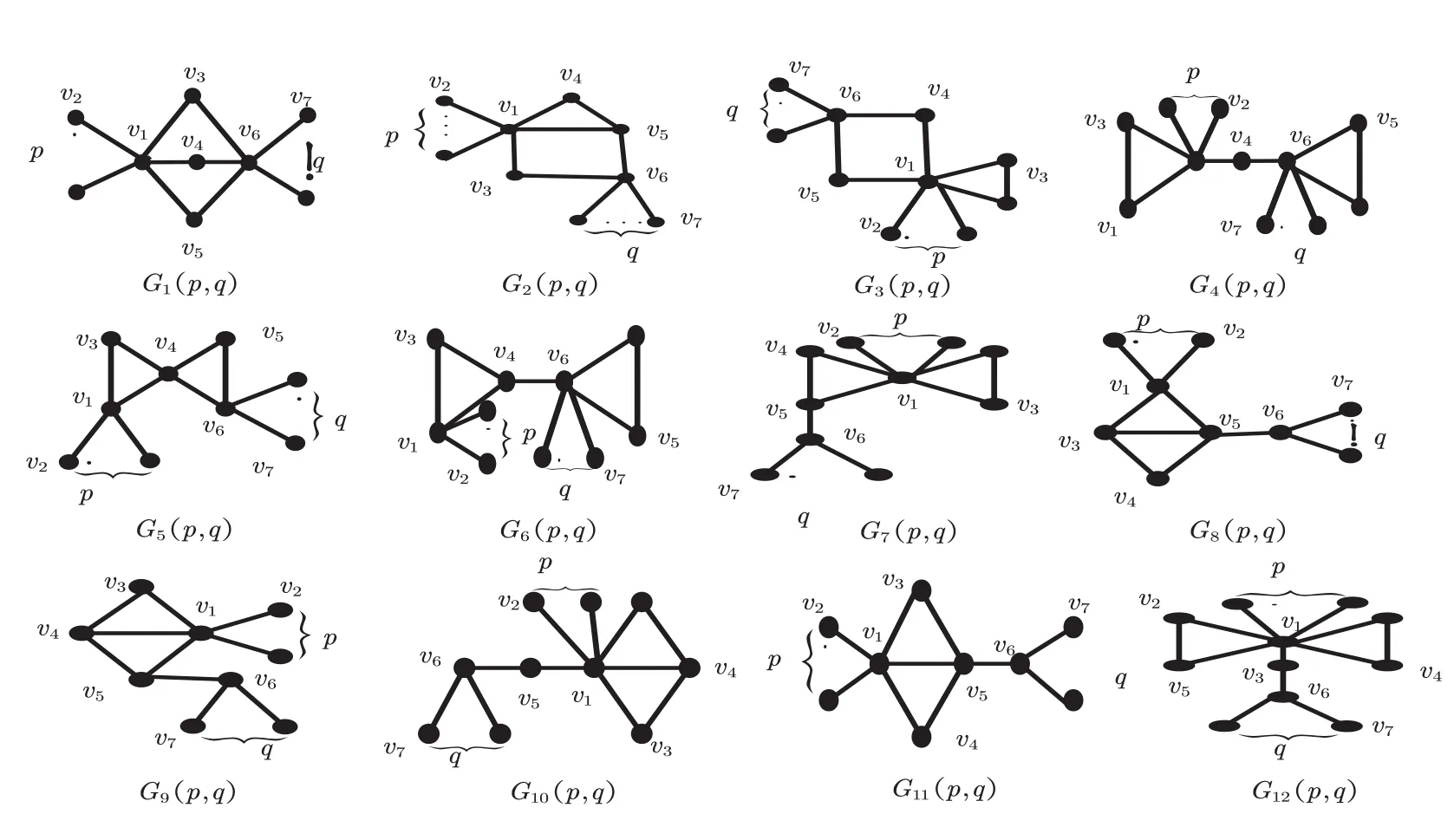
图1 Gk(p,q)(1 ≤k ≤12)
我们令b-图是由一条路和两个不相交的圈组成的图,其路的两个端点分别属于两个不相交的圈中的点。令∞-图是由两个相交的圈组成的图,其只有一个公共的交点。令θ-图是由两个相交的圈组成的图,其中至少有两个交点。显然,双圈图是b-图,∞-图和θ-图其中一个粘贴树而得到的图。
设G是一个带有n个点的图,其中v1vl1vl2···vltvn是v1和vn在图G中最短的路。令X= (X1,X2,···,Xn)T,其中X1> 0 和Xn< 0。在图G中,如果(X1+Xl2)2≥(Xn+Xl1)2,那么删除边vl1vl2,同时增加边v1vl2,否则就增加边vnvl1,我们称上述过程为图G的T1-变换。通过对图G做一系列T1-变换得到的结果图记为GT1,现在我们使用T1-变换证明下面结论。
引理2设H′={Gk(p,q)|1≤k ≤12}。若Gc ∈,则GT1∈H′,或者dGT1(v1,vn)≤2。
证明 如果G ∈H′或dG(v1,vn)≤2,那么结论自然成立。假设G/∈H′且dG(v1,vn)>2,则可分四种情况进行讨论。
情况1v1和vn在图G的同一个圈上。
对图G一直做T1-变换可知,dGT1(v1,vn)≤2。
情况2v1和vn分别属于图G的两个圈。
显然,图G是b-图或∞-图粘贴树而得到的。对G做一系列T1-变换可得,结果图GT1是由θ-粘贴树而得到的或者dGT1(v1,vn)≤dG(v1,vn)−1。如果前者成立,那么根据情况1 可证结论是正确的,否则重复上述过程,最终可以确定,结论是正确的。
情况3v1和vn分别在图G的圈上和树上。
不失一般性的假设v1在树上和vn在圈上,对图G做一系列的T1-变换可得,v1和vn是在GT1的同一个圈上,或者dGT1(v1,vn)≤dG(v1,vn)−1。如果前者成立,那么根据情况1 可证结论是正确的,否则重复上述过程,最终可以确定,结论是正确的。
情况4v1和vn都在图G的树上。
对图G做一系列T1-变换可得,v1和vn分别在图GT1的圈上和树上,或dGT1(v1,vn)≤dG(v1,vn)−1。如果前者成立,那么根据情况3 可证结论是正确的,否则重复上述过程,最终可以确定,结论是正确的。
如果X=(X1,X2,···,Xn)T满足XTQ(G)X=λ(G),那么称X是G的单位无符号拉普拉斯特征向量,这样对于任意1≤i ≤n,有
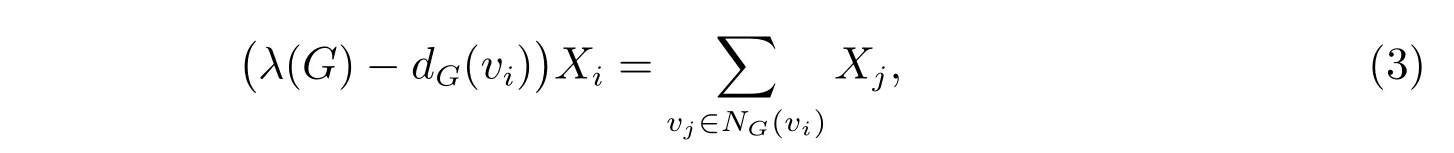
其中NG(vi)是图G中点vi的邻域,方程(3)也被称为图G的无符号拉普拉斯特征方程。
令In是一个n阶单位矩阵,则Q(G)−λ(G)In是一个半正定矩阵,所以我们可以令X= (X1,X2,···,Xn)T是图G的一个单位无符号拉普拉斯特征向量,且X1≥X2≥···≥Xn,这时X1>0 和Xn<0。
令θ4和θ5分别是带有4 个点和5 个点的θ-图,令∞5和∞6分别是带有5 个点和6 个点的∞-图,令b6和b7分别是带有6 个点和7 个点的b-图,并且这些图的两个圈的长度都是3。
设带有n个点的图H是从θ4、θ5、∞5、∞6、b6和b7中一个粘贴树而得到的,我们可以找到一个悬挂点vs,并且它的邻点vt既不是v1也不是vn。令X=(X1,X2,···,Xn)T,其中X1>0 和Xn<0。在图H中,如果(X1+Xs)2≥(Xn+Xs)2,那么删除边vtvs,同时增加边v1vs,否则就增加边vnvs,我们称上述过程是图H的T2-变换,对图H做一系列的T2-变换得到的结果图记为HT2。结合T1-变换和T2-变换可证下面重要结论。
令图Hi(1≤i ≤7),如图2 所示vn。
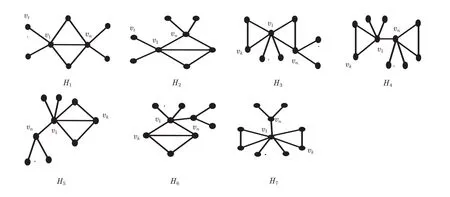
图2 Hi(1 ≤i ≤7)
引理3设H′={Hi|1≤i ≤7},图Gc ∈Ccn(n ≥12),则存在图H ∈H′∪H′′,满足λ(Gc)≥λ(Hc)。
证明 记H=H′∪H′′,让X= (X1,X2,···,Xn)T是Gc的单位无符号拉普拉斯特征向量,其中X1≥X2≥··· ≥Xn,这时X1> 0 和Xn< 0。如果G ∈H,那么结论自然成立。因此,假设G/∈H。
如果dG(v1,vn)> 2,那么对G做一系列T1-变换得到的结果图记为GT1。结合引理2 可知,GT1∈H,或GT1/∈H,但dGT1(v1,vn)≤2。如果是前者成立,那么结合方程(1)和引理1,可得
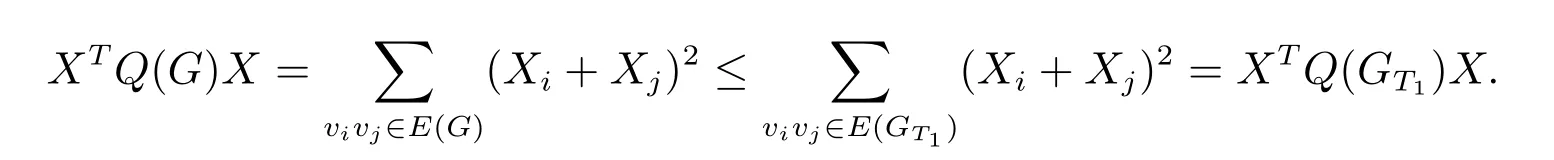
现在假设后者成立,则分两种情况讨论GT1。
情况1dGT1(v1,vn)=1。
情况1.1v1和vn在同一个带有t+2 个点的圈Ct+2上。
当t ≥2 时,可以令Ct+2=v1vnvl1vl2···vltv1。如果(X1+Xl1)2≥(Xn+Xl2)2,那么删除边vl1vl2和增加边v1vl1,否则增加边vnvl2,在做一系列上述变换后可得一个包含圈C3=v1vnvl1v1的图。设vs1vs2···vskvs1是图G11的另一个圈,则如果(X1+Xs2)2≥(Xn+Xs1)2,那么删除边vs1vs2和增加边v1vs2,否则增加边vnvs1,通过做一系列上述变换得到的图~G同构于θ4或∞5粘贴树而得到的图。如果~G/∈H,那么通过对图~G做一系列T2-变换得到的图~GT2是同构于图2 的H1、H2和H3中某一个图。
情况1.2v1和vn分别在不同的圈上。
显然,GT1是由b-图粘贴树而得到的。设GT1包含圈Ct+1=v1vl1vl2···vltv1,则当t ≥3 时,如果(X1+Xl2)2≥(Xn+Xl1)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl1可得图。如果v1和vn是在 图G21的同一个圈上,那么可以使用情况1.1,否则继续做一系列上述变换可得一个包含圈C3=v1vl1vl2v1的图。设vnvs1vs2···vskvn是图的另一个圈,如果(Xn+Xs2)2≥(X1+Xs1)2,那么删除边vs1vs2和增加边vnvs2,否则增加边v1vs1可得图。如果v1和vn在图G23的同一个圈上,那么可使用情况1.1,否则继续通过做一系列上述变换得到的图是b6粘贴树而得到的。如果/∈H,那么通过对做一系列T2-变换得到的图是同构于图2 中H4。
情况1.3v1和vn分别在圈上和树上。
不失一般性的假设v1在圈上和vn在树上,否则将X替换为−X,则GT1包含圈Ct+1=v1vl1vl2···vltv1。当t ≥3 时,如果(X1+Xl2)2≥(Xn+Xl1)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl1可得图G31。如果v1和vn在图的同一个圈上,那么可使用情况1.1,否则继续做一系列上述变换可得一个包含圈C3=v1vl1vl2v1的图。设vs1vs2···vskvs1是图的另一个圈,则如果(X1+Xs2)2≥(Xn+Xs1)2,那么删除边vs1vs2和增加边v1vs2,否则增加边vnvs1可得图。如 果v1和vn属 于中的圈,那么可以使用情况1.1 或情况1.2,否则继续通过做一系列上述变换得到的图是θ4或∞5粘贴树而得到的。如果/∈H,那么通过对图做一系列T2-变换得到的图是同构于图2 的H5、H6和H7中一个粘贴树而得到的图。
情况1.4v1和vn在同一个树T上。
设树T粘贴在圈Ck中点vlm,现考察路vnv1vl1vl2···vlm。如果(X1+Xl2)2≥(Xn+Xl2)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl2,在做一系列上述变换后可知道,点vl1是在圈vl1vs2···vskvl1上。如果(X1+Xs2)2≥(Xn+Xs2)2,那么删除边vl1vs2
和增加边v1vs2,否则增加边vnvs2可得图。这时,在图中,点v1和点vn是在同一个圈上或者点v1和点vn分别在圈上和树上。如果前者成立,那么使用情况1.1,否则就使用情况1.3。
情况2dGT1(v1,vn)=2。
情况2.1v1和vn在同一个圈Ct+3上。
当t ≥2 时,可以设Ct+3=v1vtvnvl1vl2···vltv1。如果(X1+Xl1)2≥(Xn+Xl2)2,那么删除边vl1vl2和增加边v1vl1,否则增加边vnvl2,通过做一系列上述变换可得一个含有圈C4=v1vtvnvl1v1的图。设vs1vs2···vskvs1是图的另一个圈,则如果(X1+Xs2)2≥(Xn+Xs1)2,那么删除边vs1vs2和增加边v1vs2,否则增加边vnvs1,通过做一系列上述变换得到的图是θ5或∞6粘贴树而得到的。如果/∈H,那么通过对做一系列T2-变换得到的图是同构于图1 的G1(p,q)、G2(p,q)和G3(p,q)中一个图。
情况2.2v1和vn分别在不同的圈上。
显然,GT1是由b-图或∞-图粘贴树而得到的图。设GT1包含圈Ct+1=v1vl1vl2···vlt v1,则当t ≥3 时,如果(X1+Xl2)2≥(Xn+Xl1)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl1可得图︿G21。如果v1和vn是在图的同一个圈上,那么可以使用情况2.1,否则继续通过做一系列上述变换可得一个包含圈C3的图。令vnvs1vs2···vskvn是图︿G22的另一个圈,如果(X1+Xs1)2≥(Xn+Xs2)2,那么删除边vs1vs2和增加边v1vs1,否则增加边vnvs2可得图。如果v1和vn在︿G23的同一个圈上,那么使用情况2.1,否则继续通过做一系列上述变换可得图是同构于∞5、b7和b6中一个粘贴树的图。如果/∈H,那么通过对做一系列T2-变换得到的图是同构于图1 的G4(p,q)、G5(p,q)和G6(p,q)中一个图。
情况2.3v1和vn分别是在圈上和树上。
不失一般性的假设v1在圈上和vn在树上,则GT1包含圈Ct+1=v1vl1vl2···vltv1。当t ≥3 时,如果(X1+Xl2)2≥(Xn+Xl1)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl1可得图︿G31。如果v1和vn在图︿G31的同一个圈上,那么可以使用情况2.1,否则继续做一系列上述变换可得一个包含圈C3=v1vl1vl2v1的图。设vs1vs2···vskvs1是的另一个圈,则如果(X1+Xs2)2≥(Xn+Xs1)2,那么删除边vs1vs2和增加边v1vs2,否则增加边vnvs1可得图。如果v1和vn在中的圈上,那么可以使用情况2.1 或情况2.2,否则继续通过做一系列上述变换得到的图是θ4或∞5粘贴树而得到的。如果/∈H,那么通过对做一系列T2-变换得到的图是同构于图1 的G7(p,q),G8(p,q),···,G12(p,q)中一个图。
情况2.4v1和vn在同一个树上。
让树T粘贴在圈Ck中点vlm上,若令vt是v1和vn的共同邻点,现在分两种情况去讨论。
情况2.4.1 假设存在路vnvtv1vl1vl2···vlm。
如果(X1+Xl2)2≥(Xn+Xl2)2,那么删除边vl1vl2和增加边v1vl2,否则增加边vnvl2,做一系列上述变换可得一个圈vl1vs2vs3···vskvl1。如果(X1+Xs2)2≥(Xn+Xs2)2,那么删除边vl1vs2和增加边v1vs2,否则增加边vnvs2可得图。这时,在图中,点v1在圈上和点vn在树上,或点v1和vn在同一个圈上。如果前者成立,那么可以使用情况2.1,如果后者成立,那么可以使用情况2.3。
情况2.4.2 假设存在路v1vtvl1vl2···vlm。
如果(X1+Xl1)2≥(Xn+Xl1)2,那么删除边vtvl1和增加边v1vl1,否则增加边vnvl1可得图。如果存在路vnvtv1vl1vl2···vlm,那么可以使用情况2.4.1,否则继续做一系列上述变换可得图vtvs2vs3···vskvt。如果(X1+Xl1)2≥(Xn+Xl1)2,那么删除边vtvl1和增加边v1vl1,否则增加边vnvl1可得图。这时,在图中,点v1和vn分别在圈上和树上,则可以使用情况2.3。
根据以上分析可得,对于任意图Gc ∈(n ≥12),存在图H ∈H′∪H′′,有
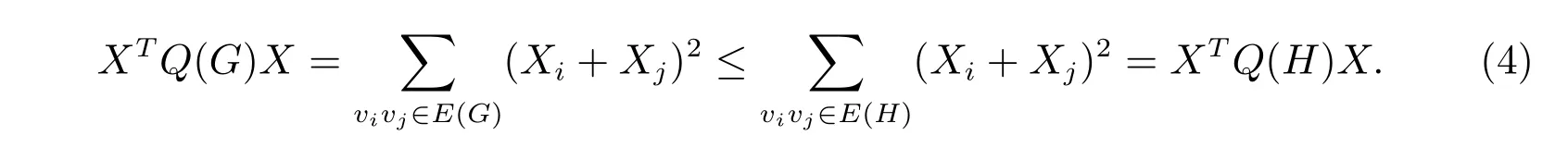
由于Q(Gc)=(n −2)In+Jn −Q(G),其中Jn是一个所有元为1 的n阶矩阵,所以使用方程(2)和(4),可得
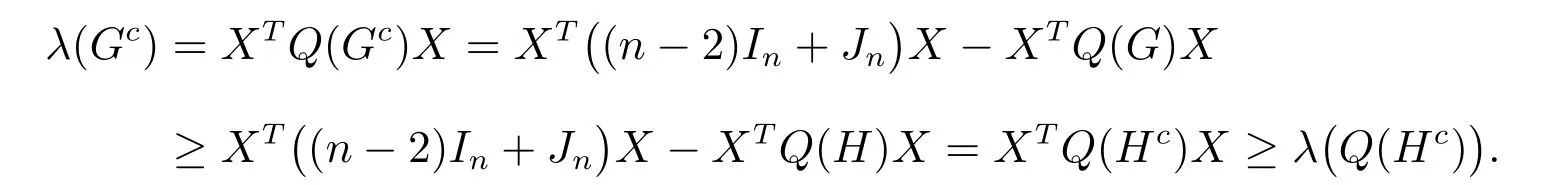
引理4如果H ∈H′′,那么存在图H∗∈H′,有λ(Hc)≥λ()。
证明 令X=(X1,X2,···,Xn)T是Hc的单位无符号拉普拉斯特征向量,其中X1≥X2≥··· ≥Xn,这时X1> 0 和Xn< 0。不失一般性的假设|Xn|≥|X1|,否则将X替换为−X。
对于图Hi ∈H′′(i= 1,2),在图H′中可以删除边v1vn和增加边vnvt得到的图H∗是同构于G1(p,q)或G2(p,q),所以
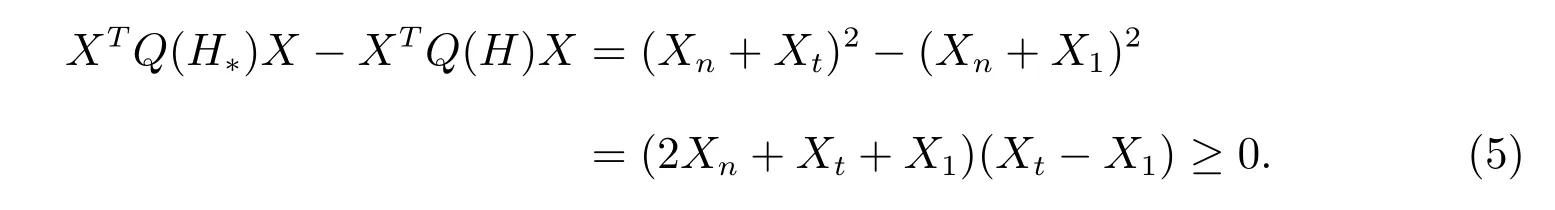
对于图Hi ∈H′′(3≤i ≤7),则删除边v1vn和增加边vnvk得到的结果图H∗是同构于Gℓ(p,q)(ℓ=2,6,7,8 或11),所以
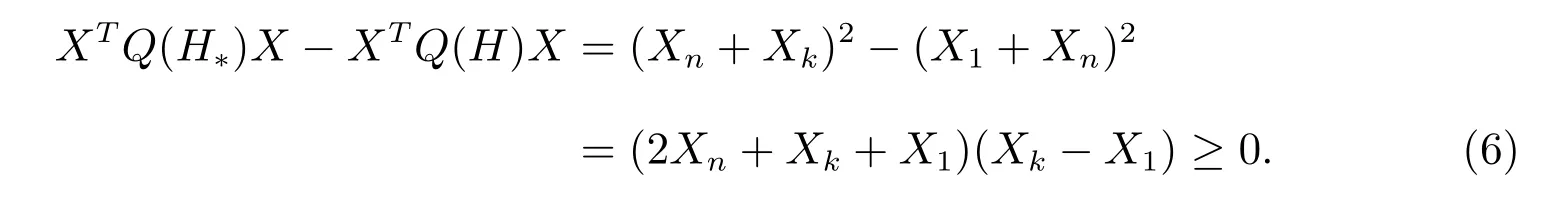
我们结合方程(2)、(5)和(6),可得
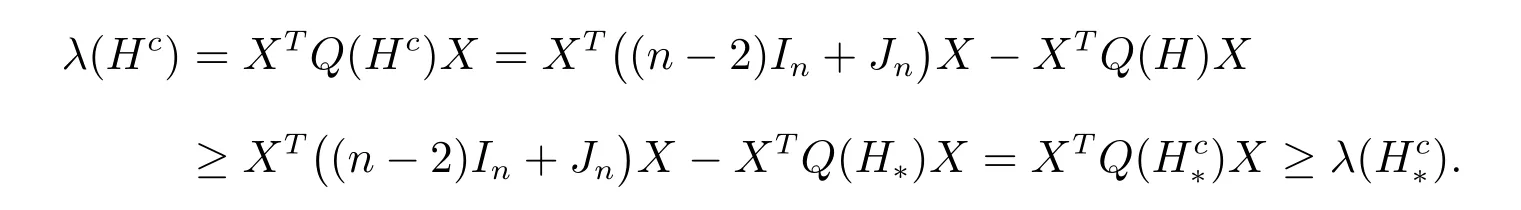
引理5[10]令G是一个简单图,则有λ(G)≤δ(G),其中
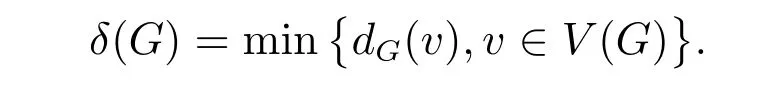
引理6设p和q是两个正整数,且p+q=n −5(n ≥12),则有
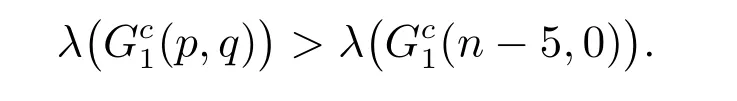
证明 不失一般性的假设p ≥q ≥1,需要求证
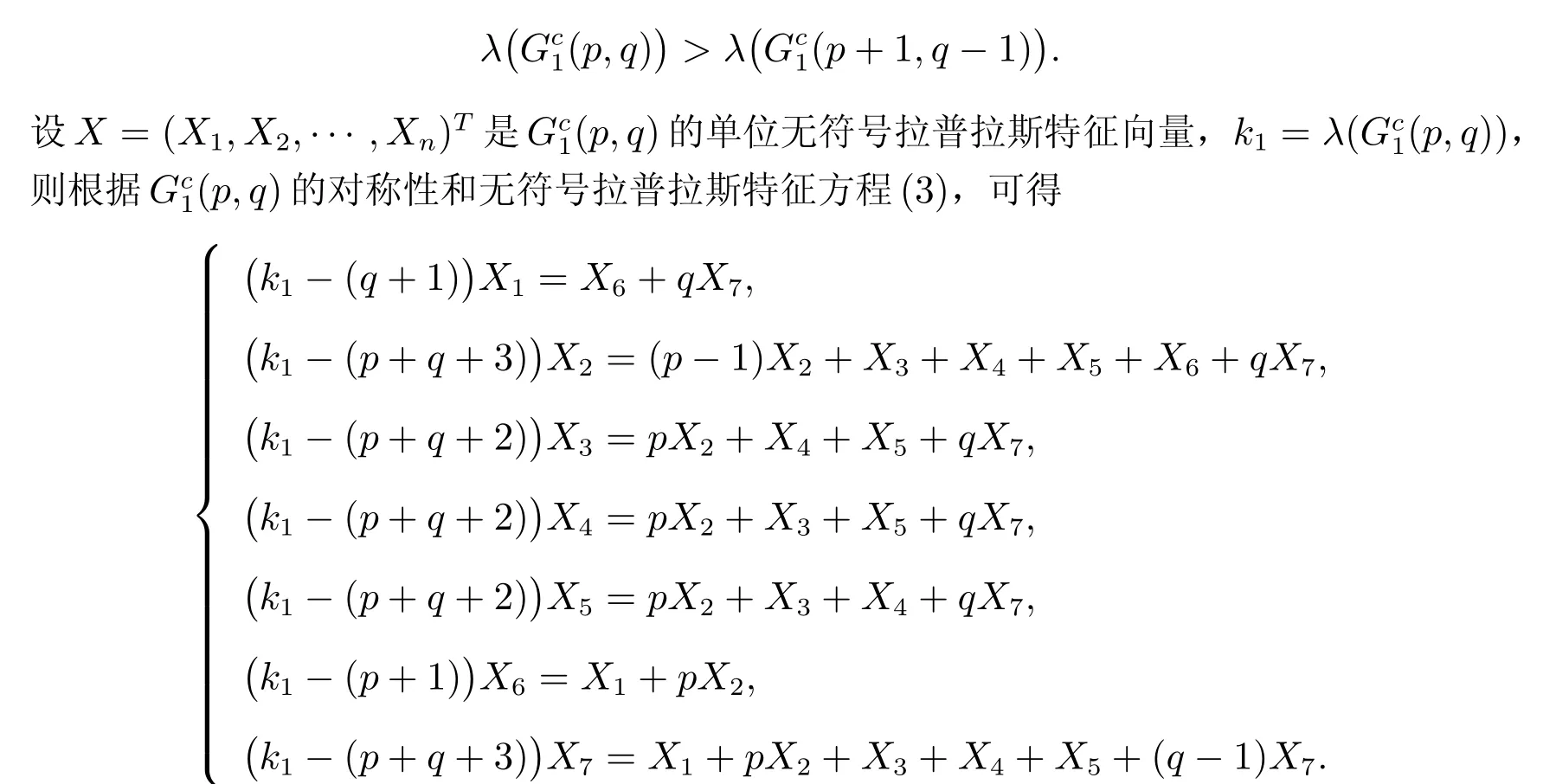
将以上方程转换成矩阵方程(k1I7−Q1)X′=0,其中X′=(X1,X2,···,X7)T和令f1(x;p,q)=det(xI7−Q1),则有
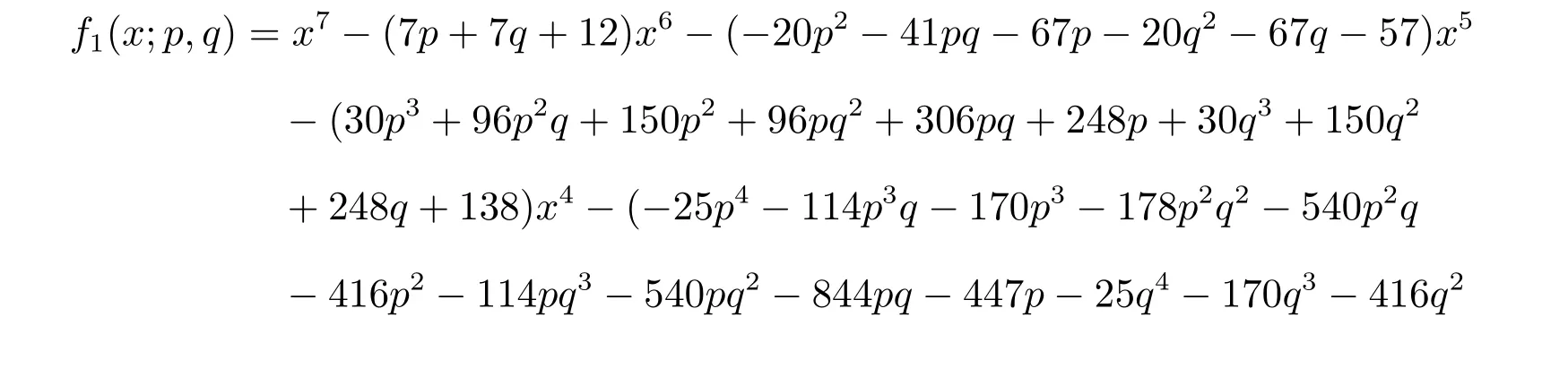
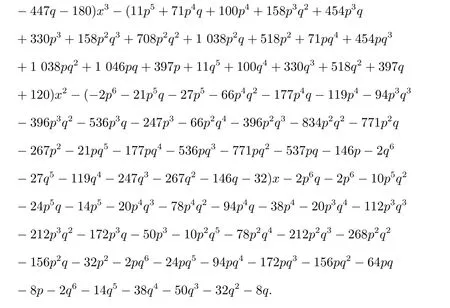
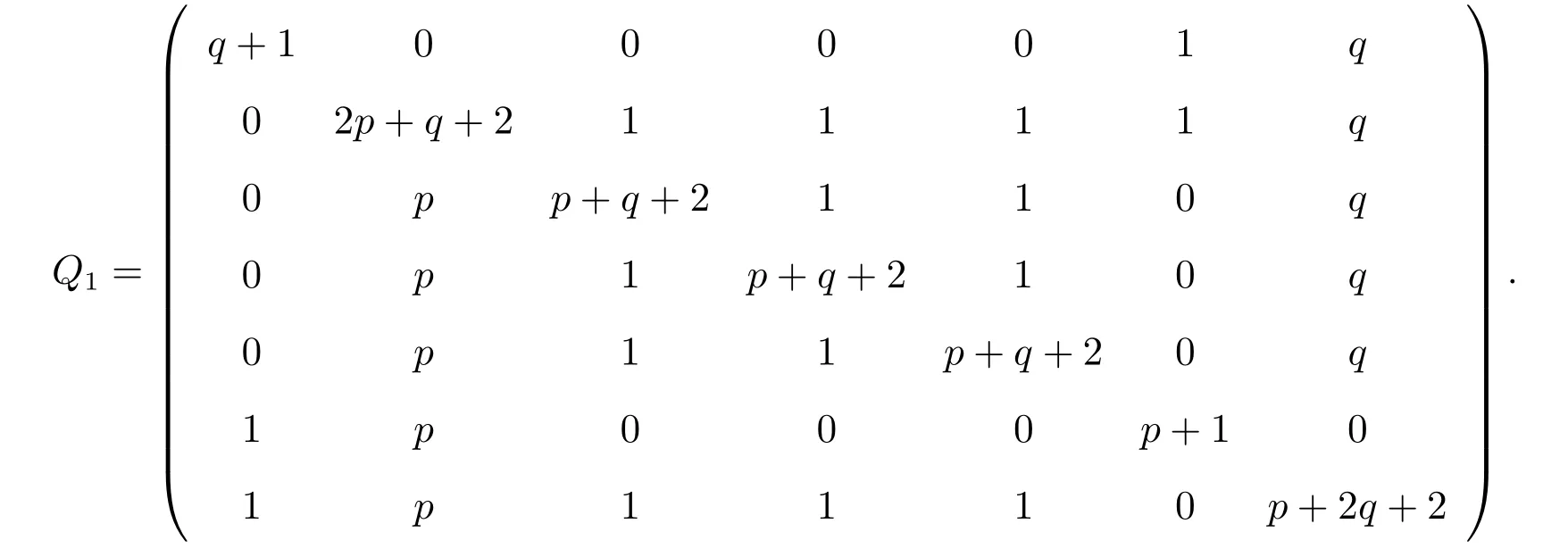
因此,有
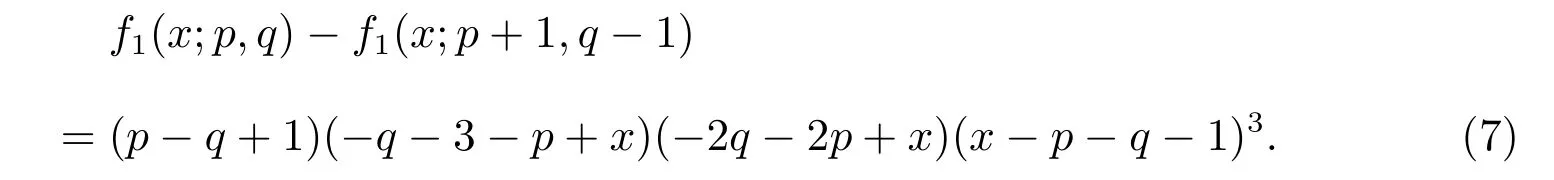
引理7设p和q是满足p+q=n −5(n ≥12)的两个正整数,则有λ((p,q))>λ((n −5,0))。
证明 令X= (X1,X2,···,Xn)T是(p,q)的单位无符号拉普拉斯特征向量,若k2=λ(p,q)),则根据(p,q)的对称性和无符号拉普拉斯特征方程(3),可得
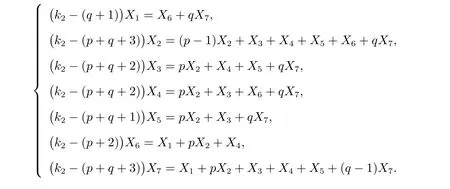
将以上方程转换成矩阵方程(k2I7−Q2)X′=0,其中X′=(X1,X2,···,X7)T和
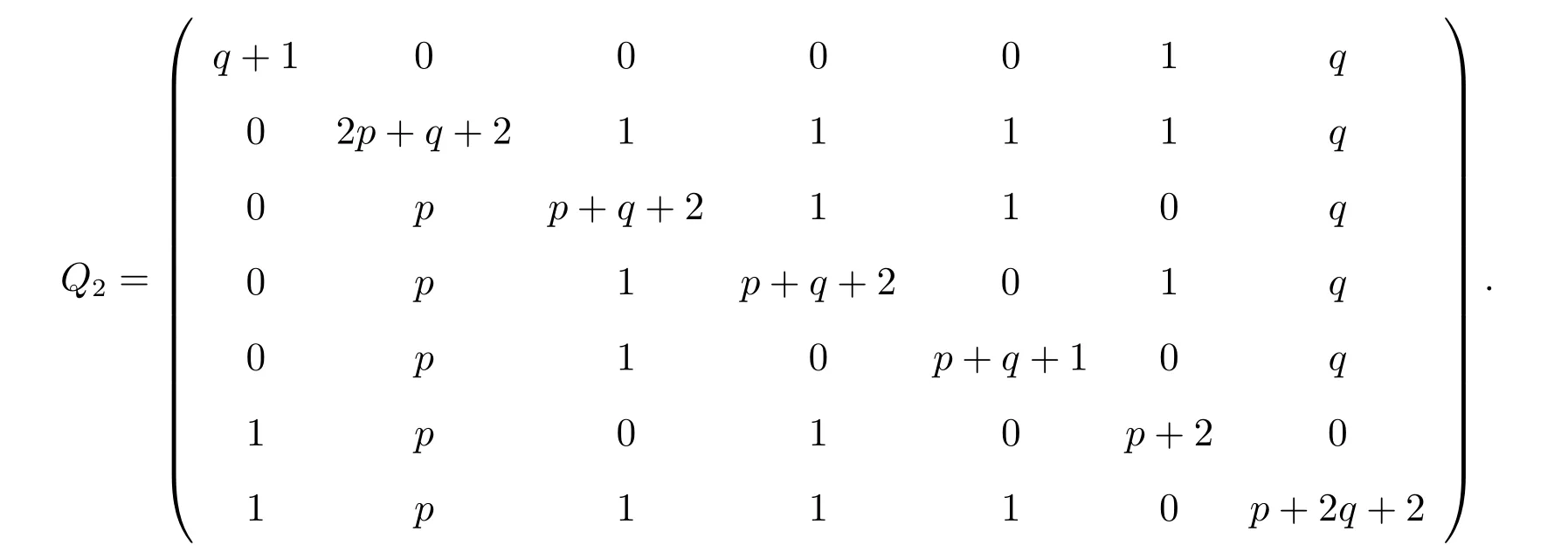
令f2(x;p,q)=det(xI7−Q2),则有
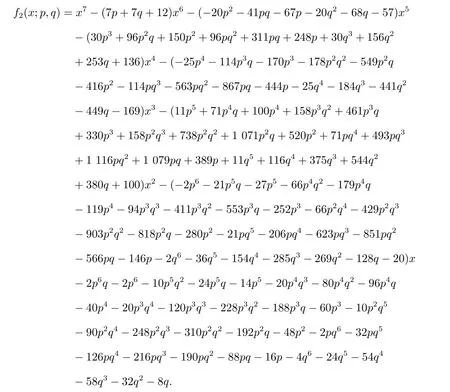
因此,有

其中

引理9设p和q是两个正整数,且有p+q=n −7(n ≥12),则有
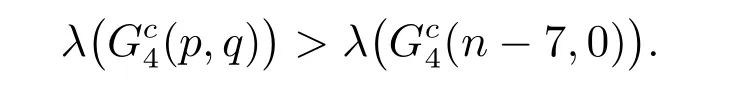
证明 不失一般性的假设p ≥q ≥1。需要求证
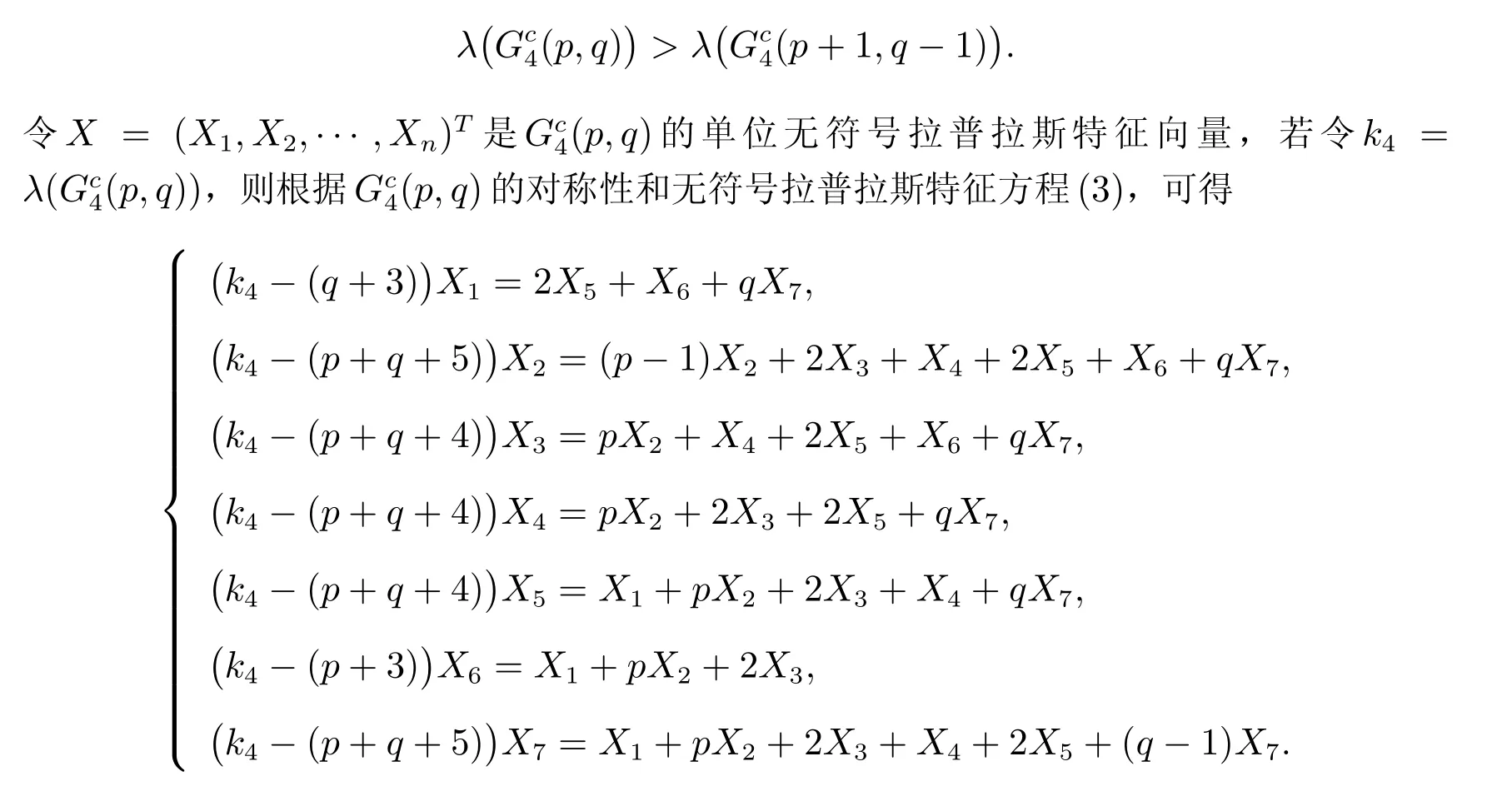
将以上方程转换成矩阵方程(k4I7−Q4)X′=0,其中X′=(X1,X2,···,X7)T和

令f4(x;p,q)=det(xI7−Q4),则有
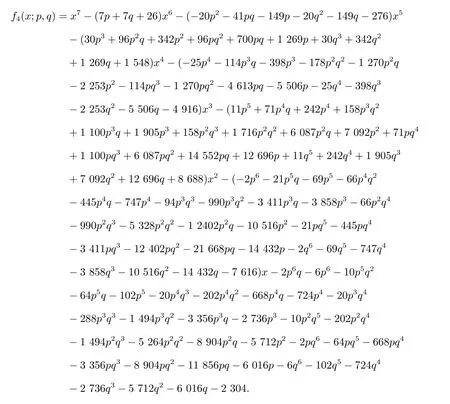
因此,有
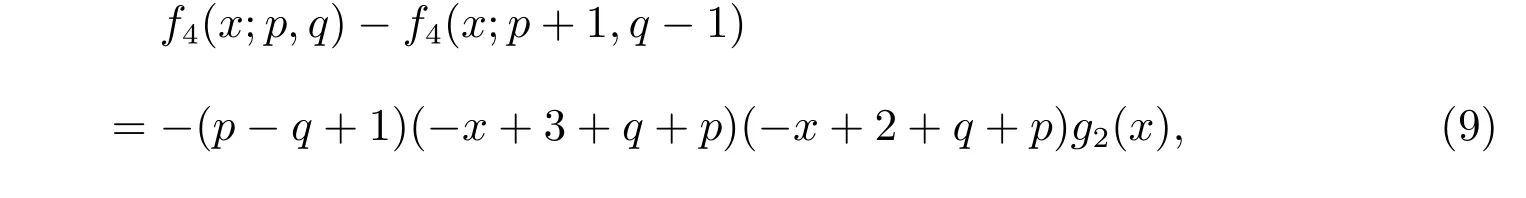
其中

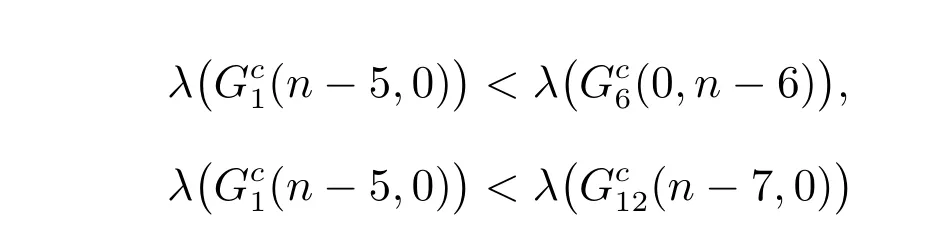
是正确的。
结合引理3、引理4 以及引理6 至引理10 中不等式,可得结论是正确的。
2 附录
事实A设g1(x)是引理7 证明中的多项式,则当0x ≤min{q+1,p+2}时,g1(x)>0。
证明 下面将对g1(x)进行求导数,可得

设min{q+1,p+2}=p+2,则有0x ≤p+2。因为p ≥0 和n=p+q+5≥12,所以n ≥2p+6,q ≥4,因此

可得g1(x)是关于x的单调递减多项式,所以
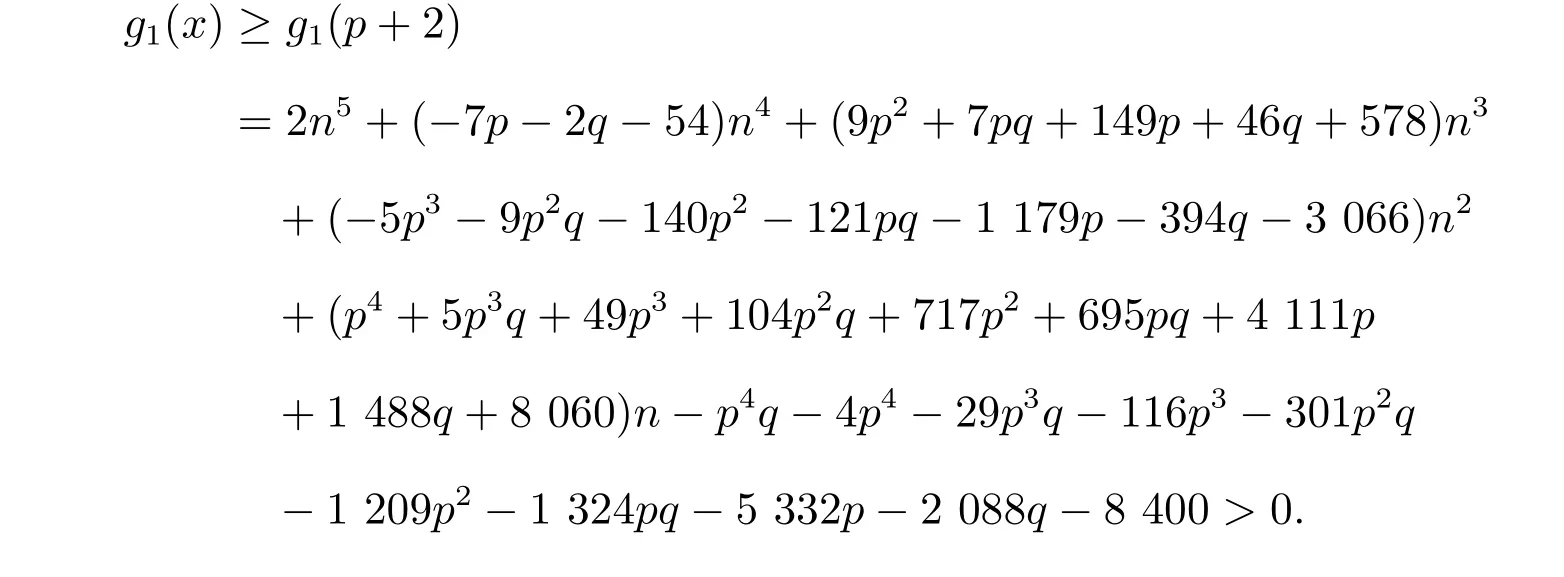
如果min{q+1,p+2}=q+1,那么0x ≤q+1,所以可得g1(x)>0。
事实B设g2(x)是引理9 证明中的多项式,则当0x ≤q+3 时,g2(x)>0。
证明 下面对g2(x)进行求导数,可得

因此g2(x)是关于x的单调递减的多项式,所以
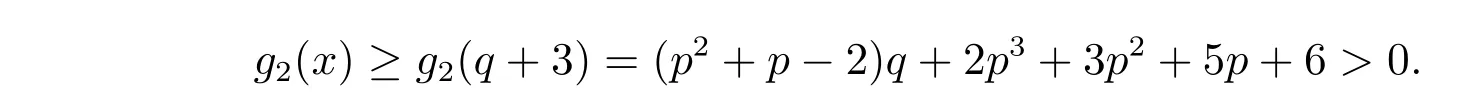
事实C设g4(x)是引理11 证明中的多项式,则当0x ≤1 时,g4(x)>0。
证明 下面对g4(x)进行求倒数,可得
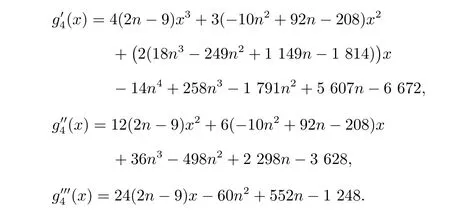

——以指数、对数函数同构问题为例

