一类多概率区间分布时滞网络控制系统分析
戎佳豪,姜偕富,张镇佳,赵 冰
(杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
网络控制系统(Networked Control Systems, NCSs)是由通信网络组成闭环回路的空间分布式控制系统[1]。相较于传统控制系统,NCSs具有远距离控制、布线方便、易扩展、维护方便等优点。但是,NCSs的控制性能受到数据传输速率、网络时延、数据丢包等网络物理局限性的影响。近几年来,针对网络控制系统网络时延的研究取得了一定成果。文献[2]把网络控制系统转化为时变时滞系统,在L-K泛函中使用增广矩阵,更好地利用了系统的时滞信息,降低了结果的保守性。文献[3]在L-K泛函中引入四重积分,使用扩展Wirtinger不等式来界定泛函求导项,取得了很好的结果,但未考虑时滞的随机性,使所得结果的保守性较大。文献[4]研究二概率时滞区间分布的问题,构造了一个概率区间时变时滞系统,在L-K泛函中引入增广矩阵和三重积分,运用Wirtinger不等式和凸组合相结合的方法来处理泛函求导项,降低了稳定性条件的保守性。文献[5]研究多概率区间时变时滞系统的稳定性问题,给出一个包含二概率区间时滞系统模型作为特例的三概率区间时滞系统模型,使用广义Finsler引理给出了一个可以获得更大时滞上界的稳定性准则。本文研究网络控制系统的诱导时延问题,在三概率区间时滞系统模型的基础上,构造带增广矩阵和三重积分、四重积分的L-K泛函,使用Wirtinger不等式和凸组合结合的方法界定泛函求导项,从而得到一个保守性较小的稳定性准则。
1 系统模型
考虑如下一类基于网络控制的线性系统:
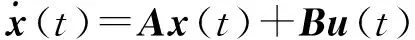
(1)
式中,x(t)∈Rn和u(t)∈Rm分别为系统的状态向量和控制输入;矩阵A和B为适合维数的参数矩阵。
假设网络控制系统中的传感器为时间驱动,控制器和执行器为事件驱动。T为传感器的采样周期,ikT为传感器的第k个采样时刻。若传感器在ikT时刻采样到信号,那么在ikT+τk时刻执行器收到来自控制器的命令,其中τk=τsc+τc+τca,τsc为传感器和控制器之间的传输时滞,τc为控制器的计算时滞,τca为控制器与执行器之间的传输时滞。
如果系统(1)可控,其网络控制器为:
(2)

(3)

(4)
式中,h(t)为系统(4)的时滞函数,h为已知常量;φ(t)为系统在区间[-h,0]的初始状态。
假设存在常量h1,h2和h3,满足0≤h1≤h2≤h3=h,h(t)在区间[0,h1],(h1,h2]和(h2,h3]上的概率分布已知,定义如下3个随机事件:
Ω1∶h(t)∈[0,h1];Ω2∶h(t)∈(h1,h2];Ω3∶h(t)∈(h2,h3]
引入如下2个随机变量:

定义3个函数h1(t)∶R+→[0,h1];h2(t)∶R+→(h1,h2];h3(t)∶R+→(h2,h3],则有:
显然,δ1(t)和δ2(t)都服从伯努利分布,满足
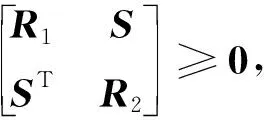
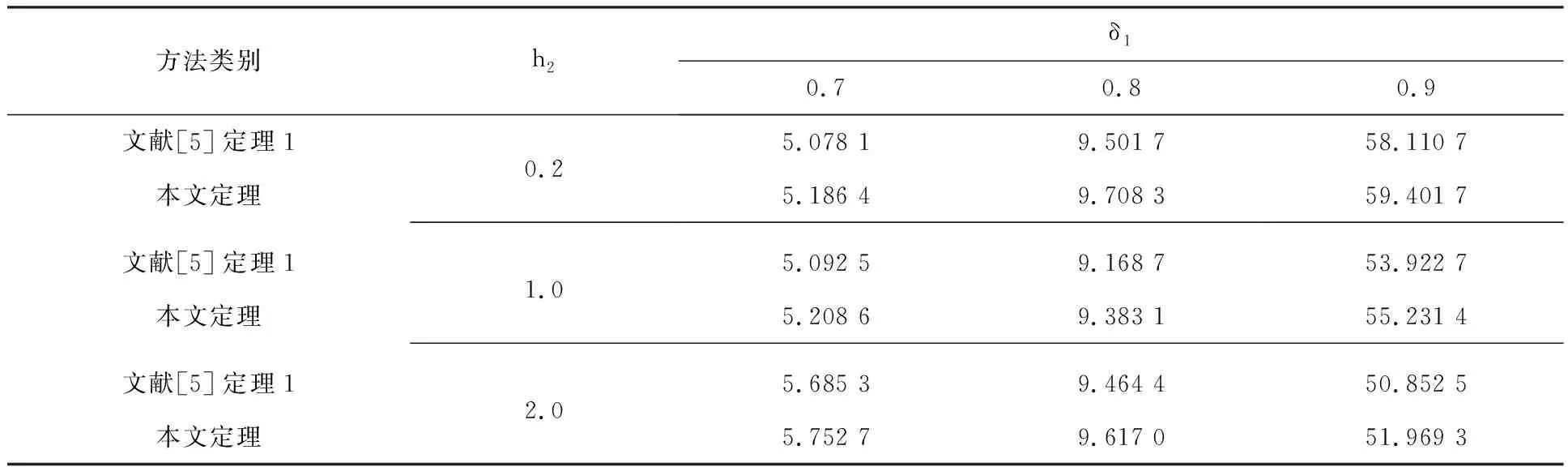
Prob{δ1(t)=1}=Prob{0≤h(t)≤h1}=E{δ1(t)}=δ1,Prob{δ1(t)=0}=Prob{h1 综上分析,系统(4)改写为: (5) 当δ1=1或δ2=1或δ1+δ2=0时,系统时滞概率分布在1个区间上;当δ1=0,δ2∈(0,1)或δ1∈(0,1),δ2=0或δ1+δ2=1,δ1∈(0,1),δ2∈(0,1)时,系统时滞概率分布在2个区间上;当δ1∈(0,1),δ2∈(0,1),且δ1+δ2∈(0,1)时,系统时滞概率分布在3个区间上。本文主要研究三概率区间分布的情况。 针对系统(5)给出如下均方稳定性准则。 (6) (7) (8) (9) 式中, Ξ12=-P12+U11-U12+U21-U22,Ξ13=δ1M1Ad-2R1-U11-U12-U21-U22,Ξ15=δ2M1Ad, 证明构造如下形式的L-K泛函 V(xt)=V1(xt)+V2(xt)+V3(xt)+V4(xt)+V5(xt) 沿系统(5)的运动轨迹做弱无穷运算,可得: V(xt)=V1(xt)+V2(xt)+V3(xt)+V4(xt)+V5(xt) (10) 式中, (11) xT(t-h2)Q2x(t-h2)-xT(t-h3)Q3x(t-h3) (12) (13) (14) (15) 引入如下零等式: (16) 运用引理1对式(13)中的R1相关积分项进行放缩,可得: (17) (18) 运用引理2对式(17)和(18)进行放缩,可得: (19) 同理可得: (20) (21) 式中, 对式(14)中Z相关积分项利用引理3可得: (22) 对式(15)中W相关积分项利用引理3可得: (23) 联立式(10)—式(23),并对式(10)求数学期望,可得: E{V(xt)}≤E{ξT(t)Ξξ(t)} 当满足Ξ<0时,存在一个足够小的常数ε>0,使得E{V(xt)}<-εE{ξT(t)ξ(t)}成立。 采用文献[9]中的类似方法,可以得到: 针对网络控制系统(1),本文将其转化为时滞系统(5)并得到稳定性准则,从而得到网络控制系统(1)的稳定性准则。在构造L-K泛函时,引入了增广矩阵和四重积分,与文献[5]相比,使用了更多的时滞信息;对L-K泛函求导时,把式(13)的3个积分项进行拆分,使用Wirtinger积分不等式界定拆分后的积分项,再用凸组合引理处理界定后的积分项,充分运用了时滞信息,有效降低了稳定性准则的保守性。 通过数例来验证本文提出的三概率区间分布时滞网络控制系统稳定性准则的有效性。采用MATLAB中的LMI工具箱求解线性矩阵不等式,得到确保系统渐近稳定的最大允许时滞上界。 使用文献[5]中的系统模型: 取h1=0.1,δ2=0.08,对不同取值的h2,δ1,分别运用文献[5]中的定理1和本文定理得到允许的最大时滞上界值如表1所示。 表1 不同的h2和δ1下,最大允许时滞上界h3 从表1可以看出,与文献[5]相比,本文定理得出的时滞上界h3更大一些,说明引入四重积分和增广矩阵降低了结果的保守性,验证了本文方法的有效性。 为了更好地验证本文定理得到的稳定性准则,表2列举了运用本文定理、文献[10]定理1、文献[11]推论2,分别在概率为0.7,0.8,0.9下求出的最大时滞上界。 算法的复杂度主要与决策变量数以及线性矩阵的行数相关,其中决策变量数对复杂度起着最主要的作用。从表2的决策变量数可以看出,本文定理算法的复杂度与文献[10]定理1和文献[11]推论2相比处于同一个数量级,但结果的保守性大大减小了。根据表2还可以看出,本文定理的最大时滞上界要大于文献[10]和文献[11],因为在界定式(13)的求导项时,本文使用了凸组合引理,并在L-K泛函构造时引入了四重积分和增广矩阵,利用了更多的时滞信息,从而得到保守性更小的均方稳定性准则,进一步验证了本文方法的有效性。 本文主要研究一类线性三概率区间分布时滞网络控制系统的均方稳定性问题。为了充分利用时滞信息,在L-K泛函中引入四重积分,使用Wirtinger积分不等式与凸组合结合的方法界定L-K泛函中二重积分求导产生的积分项,使用Jensen不等式界定L-K泛函中三重积分四重积分求导产生的积分项,得到保守性更小的稳定性准则。但是,在实际应用中,网络控制系统往往是非线性的,下一步将基于T-S模糊模型研究一类非线性多概率区间分布时滞网络控制系统问题。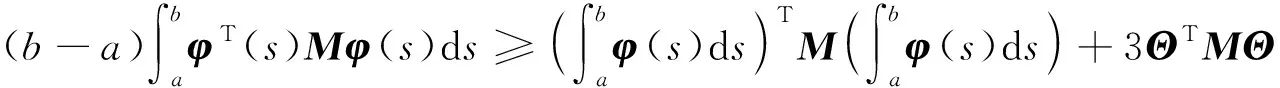
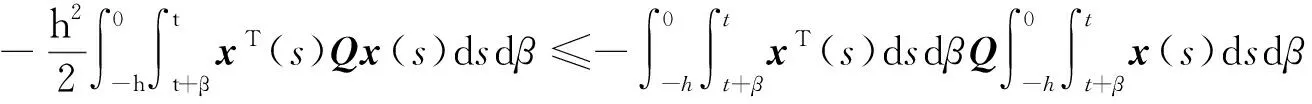
2 主要结果
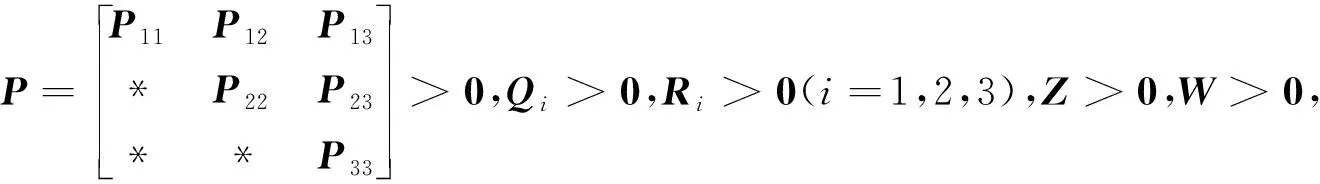
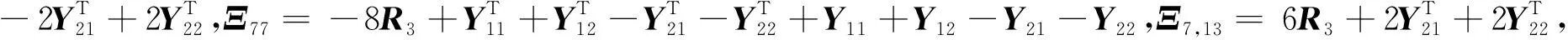
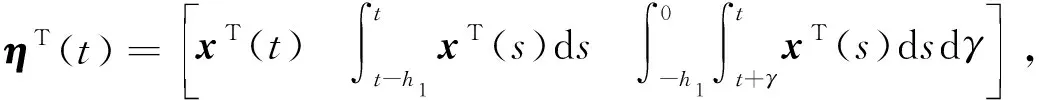
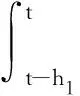


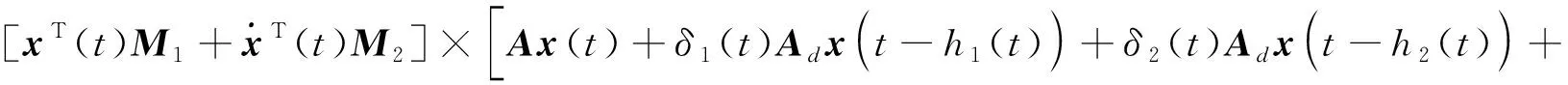
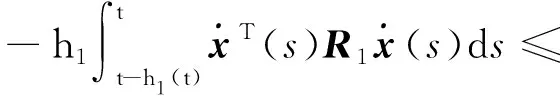
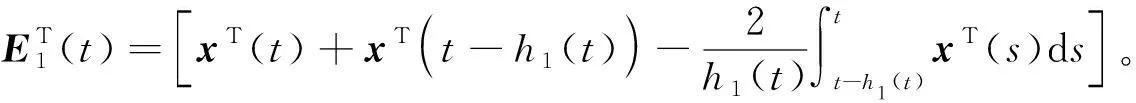
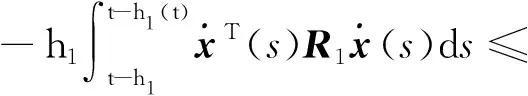
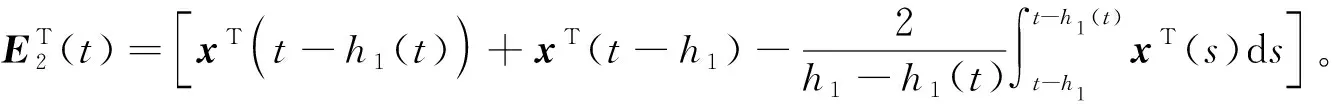
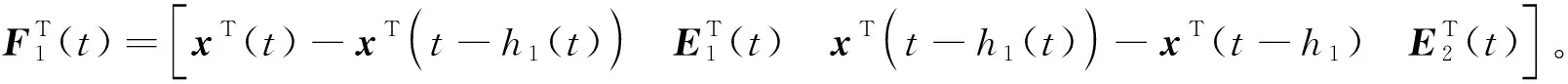

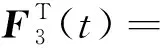
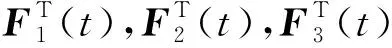
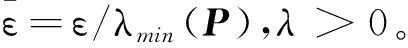
3 数例验证
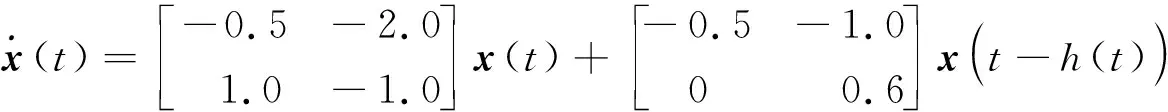
4 结束语

