非齐次弹性力学问题双互易边界元方法研究*

潘先云，余江鸿,2，周枫林

（1.湖南工业大学 机械工程学院，湖南 株洲 412007；2.长沙理工大学 公路工程教育部重点实验室，长沙 410001）

引 言

在一些工程实践中，人们选择运用数值计算方法分析复杂结构的弹性力学、热传导等各方面问题，为工程设计提供依据和参考.目前发展较好的数值计算方法有：有限单元法[1]、无网格法[2]、边界元法[3-4].相较于其他数值计算方法，边界元法只需要离散问题的边界而不是整个区域，从而降低了维数减少了计算工作量，其计算效率高.此外，边界元还具有计算精度高、能有效处理无限域的问题等优势.如胡宗军等[5]用高阶边界元分析了二维薄体结构温度场；李聪等[6]用扩展边界元法求解了双材料裂纹结构全域应力场.另外，边界元在弹性力学方面也有着广泛的应用.

边界元法在弹性力学问题[7]方面的运用可以追溯到20世纪初.1905年，Fredholm[8]提出运用积分方程求解弹性力学问题.到了20世纪60年代末，Rizzo 等[9]和Cruse[10]运用直接边界元法求解弹性力学问题.我国学者也在弹性力学边界元方面开展了大量研究.孙秀山等[11]提出用边界元法解决二维正交各向异性结构弹塑性问题；姜弘道[12]完整地介绍了利用边界元法解决弹性力学问题.但是传统边界元法对于处理非线性和非均质的域积分面临较大困难，比如含有体力、时间相关效应和其他问题上，通常需要将问题域分成内部单元，生成的边界积分方程则会出现域内积分项，因此边界元方法失去了原有的降维优势.为了解决域积分问题，人们进行了大量的研究来寻找一种将区域积分转化为等价边界积分的通用而有效的方法，并提出下列3 种方法：双互易法（DRM）[13]、多重互易法（MRM）[14]和径向积分法（RIM）[15].双互易法主要是基于微分算子特解将区域积分转换为边界积分，从而解决了域内积分项的问题.高锁文等[16]将双互易方法与边界元结合，对开孔无限大薄板弹性波的散射与动应力集中问题进行了分析；苗雨等[17]提出双互易法解决弹性动力学问题.双互易法还在声学[18]、热学[19]等多个领域有着广泛的应用.

双互易方法一般选取RBF[20]作为插值函数.RBF 分为全局型RBF 和紧凑型RBF，无论是哪一种RBF，形状参数和插值点数量对其插值精度和稳定性都有重要影响.Franke[21]最先提出用RBF 作为插值函数的插值方法.从此，RBF 插值方法不断发展和完善.我国学者也采用RBF 来解决各种问题，赵培玉[22]用RBF 求解椭圆型偏微分方程；聂鑫[23]将其应用在电磁学领域；曾华等[24]利用multiquadric(MQ)函数作为RBF处理非均匀弹性力学问题.RBF 方法不仅形式简单，而且精度高，数据拟合好，较其他方法而言，具有一定的优势.但是RBF 还存在一些问题，比如插值的稳定性和精度问题，插值函数中形状参数的取值问题等，本文接下来将对其中一种RBF 探讨上述问题.

本文应用双互易边界元法(DRBEM)解决弹性力学中含有域内体力项的问题.弹性力学边界积分方程中将体力项用RBF 来插值，再导入到弹性力学边界积分方程中，得到完全边界积分方程，然后对边界积分方程进行离散得到线性方程组或者非线性方程组，最后求解方程组.在此过程中，RBF的选择对于插值精度和双互易边界元方法数值计算精度至关重要.本文提出选择指数型RBF[25]，探讨指数型插值函数的形状参数变化方案对插值精度和稳定性的影响.然后再应用到双互易边界元方法中，通过边界元程序产生的数值分析结果进行稳定性和精度讨论，并验证了指数型基函数作为双互易边界元方法RBF 解决弹性力学域内体力项问题的有效性.

1 RBF 插值

1.1 RBF 定义

RBF 插值就是用RBF的线性组合近似表示未知函数，对N个不同的点构成的三维空间{x1,x2,···,xN}⊆R有

RBF 采用以下形式：

在N个点上构造函数：

式中，i=1,2,3,···,N.那么就可以得到线性方程组：

1.2 RBF的类型

RBF 有很多种，我们常见的全局型RBF 如下所示：

指数型RBF：

本文选择指数型基函数作为双互易边界元法的指数型RBF，形状参数变化方案为

2 静弹性问题双互易边界元法

2.1 静弹性力学问题

根据弹性力学基本方程（平衡微分方程、几何方程和物理方程）可建立以位移为未知物理量的位移Navier 控制方程，其微分表达式形如

式中，G为剪切模量，v为Poisson 比，fj为第j方向上的体力，Ω为结构所在整个区域.为完全求解出所有位置上的位移分量或者应力分量，往往还需要添加确定的边界条件，其位移边界条件和 应力边界条件如下所示：

式中，uj为第j个方向的位移；pj为第j个方向的面力；n为边界上单位外法向量；为Γu上的位移边界条件；为Γp上的应力边界条件，区域边界Γ 满足Γ=Γu∪Γp.

2.2 双互易边界元法

双互易边界元法是解决边界积分方程中含非均匀体力项积分计算困难的有效途径之一，它的中心思想是借助RBF 插值技术对非均匀体力项函数进行插值处理，将非均匀体力项积分转换为边界积分，成功避免了域内积分的计算，还原了边界元法仅需边界离散的特征.

基于Betti 定理与Kevin 基本解得到静弹性问题边界积分方程，形如

式中，p*lk为面力基本解；u*lk为位移基本解；clk与源点的位置有关，具体表达式如下：

θ为源点处的立体角角度；

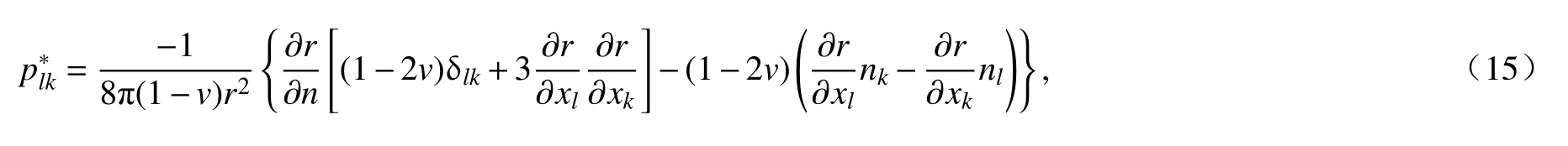
其中

在实际问题中，体力载荷不可避免，若要直接进行域内体力项积分的运算将会严重影响到边界元方法的计算效率，为体现边界元法只含边界网格的优势，本文采用了双互易法对体力积分进行转换.式（12）中出现域内体力项fk，结合RBF 对式（12）中的体力项进行插值处理，插值表达式为

式中，φj为未知的系数，ϕj为插值函数，N和L分别是边界点和内部点的数量.值得注意的是，若体力项函数未知，则RBF 插值系数也是未知的.找到方程（10）中特定的位移u满足Navier 平衡方程：

式中，δmk为Kronecker 函数.

利用分部积分可以将体力项积分写成

将式（22）代入到式（12）中可以得到含体力的静弹性问题双互易边界积分方程：

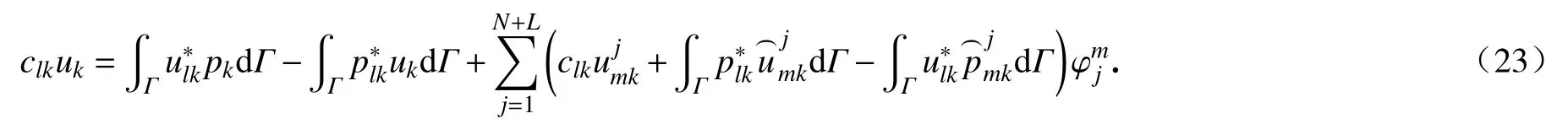
双互易法的实现往往要借助于RBF 插值，对于式（20）的RBF ϕj采用指数型RBF，其表达式为

其中，c为形状参数，r为插值点与节点的距离.对应的指数型RBF 在弹性问题上的位移特解即式（21）中特定位移u的表达式为

式中

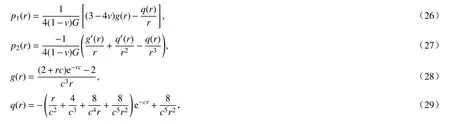
特解（25）并不是唯一的，该特解是通过Papkovich 势函数法推导出来的满足平衡方程的一种形式，并且保证了g（r）与q（r）在全域内连续且有一阶导数.将位移特解（25）导入Hooke 定律与平衡方程同样可以求解出应变特解与面力特解：

2.3 边界离散与数理处理

通过式（23）可以看出双互易边界元法求解静弹性问题时并没有使用到域内积分，所以只需要在边界上进行单元离散，经过离散后式（23）可以写成

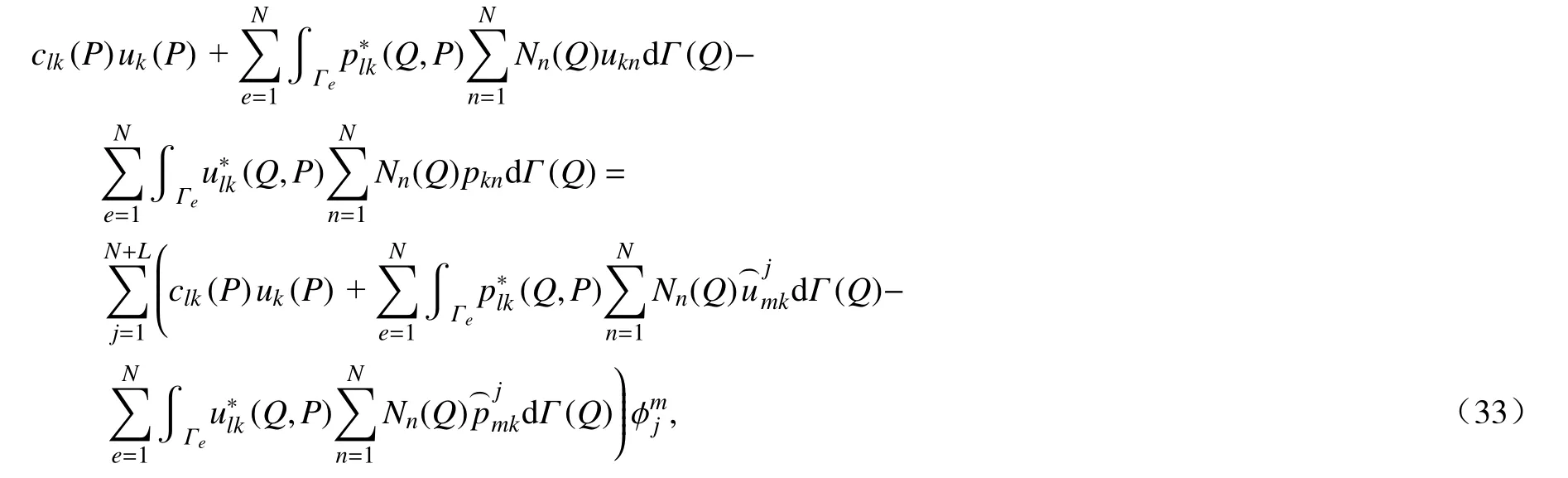
式中，Γe为第e个单元的边界.在单元内任意一点的位移和面力可以表示为

离散后得到线性方程组：

将所有未知量移到方程的左边整理可得

通过式（37）可以计算得到所有点对应的位移分量或面力分量.

3 数值算例

在实际工程问题分析中,插值的精度和稳定性不可同时兼得的矛盾已有定论，数值分析的稳定性往往比计算精度更为重要.因为精度可以通过增加自由度来提高，而一旦出现数值稳定性问题，就会导致计算出错.因此，可以通过改变RBF的形状参数，在保持精度可接受的情况下，提高插值的稳定性.

插值的性能取决于参数的变化方案，因此本文提出的参数变化方案不同于恒定参数，而是为提高插值稳定性，插值函数的形状参数取决于插值点间最小距离的最小值，也就是式（9）提出的插值方案.针对这种参数变化方案，本文设计了四个算例.

第一个算例为分析RBF 插值精度和插值稳定性的变化.第二个和第三个算例在有解析解的情况下，将指数型基函数应用到双互易边界元方法中分析结构静弹性力学问题，验证双互易边界元法采用指数型插值方法处理弹性力学中域内体力项问题的有效性.第四个算例在无解析解实际工况下，用双互易边界元法和有限元法两种方法分析结构静弹性力学问题.本文中四个算例都是通过在Visual Studio的软件环境下，设计边界元法程序分析得到的数值结果.

相对误差定义为

式中，v为相关变量向量，vei为数值解，vai为解析解，|v|max为解析解中的最大值，N为节点的数量.

条件数反映的是数值方法的病态程度，采用条件数来评判数值方法的稳定性，条件数越大，病态越严重.对于一般的矩阵，条件数都为1，而边界积分方程所构造的矩阵往往都是奇异矩阵，条件数很大，问题往往都是“病态”的，病态的程度可以通过条件数的大小来反映，条件数越大，表明函数越不收敛，数值方法越不稳定，可以通过对比条件数的计算结果验证方法的稳定性.

3.1 RBF 插值精度和稳定性分析

本算例模型为边长为2的正方体，正方体中心处于直角坐标系原点，插值点位置如图1所示.被插值函数分别为

图1 正方体RBF 插值点位置Fig.1 Positions of RBF interpolation points in a cube

本算例中通过改变正方体中指数型插值函数的插值点数量，研究在不同被插值函数中的插值精度和插值稳定性变化，得到插值点数量的变化对插值精度和稳定性的影响.

图2和图3分别表示RBF 插值相对误差和RBF 矩阵条件数随着插值点数量增加的变化情况.图2所示的收敛性分析说明了随着插值点的不断加密,插值精度不断提高.我们可以了解到RBF 矩阵条件数表示插值稳定性，即RBF 矩阵条件数越大，插值稳定性越差.所以从图3的结果上来看，插值点数量越多时，RBF 矩阵条件数越大，插值稳定性越差.

图2 正方体RBF 插值精度Fig.2 Accuracies of the cube RBF interpolation

图3 正方体RBF 矩阵条件数Fig.3 The condition number of the cube RBF matrix

3.2 双互易边界元数值分析

3.2.1 球体模型

本算例是在有解析解的情况下，利用双互易边界元方法对正方体模型进行静力学分析，双互易边界元方法中采用指数型基函数中式（9）的插值方案，验证指数型插值函数作为双互易边界元方法中RBF 去解决弹性力学中域内体力项问题的有效性.本算例模型为半径为2的球体，插值点位置如图4所示，材料参数为：密度1.14，Poisson 比0.25，弹性模量1.0.

图4 球体插值点位置Fig.4 The sphere interpolation point positions

弯管的边界条件和位移解析解为

体力项函数分布为

在双互易边界元法中，插值点数量变化对所有节点上面力相对误差和插值稳定性的影响如图5和图6所示.随着插值点数量增多，所有节点上面力相对误差降低，双互易方法的计算精度不断提高，但是稳定性有所变差.从算例结果可以看出，计算精度和稳定性随着插值点数量增多不断收敛，插值点数量达到7 369 后，矩阵条件数随插值点数量增加的速度明显减慢并趋于稳定.因此，使用式（9）控制形状参数能够有效控制插值矩阵条件数的快速增长,同时也能够达到很高的插值精度.

图5 边界上面力的相对误差Fig.5 Relative errors of the surface force on the boundary

图6 RBF 矩阵条件数Fig.6 The condition number of the RBF matrix

3.2.2 弯管模型

为了进一步验证形状参数插值方案在双互易边界元方法解决弹性力学中域内体力项问题的有效性是否具有普遍性，设计了复杂模型弯管，几何尺寸如图7所示，插值点位置见图8.取样点数为81个，取样点位置如图9所示，其中边界取样点为31个，位于R=0.8 mm 倒角面上均匀选取一圈，起点坐标为（-5.566,0.234 3,0）；域内为50个，位于R=0.8 mm 第一段倒角处薄壁中面圆周一圈，起点坐标为（-6.032,0.4,0.501 3）.弯管材料参数为：Poisson 比0.25，弹性模量1 MPa，材料密度1.14 t/mm3.

图7 弯管几何图示(单位：mm)Fig.7 The geometric model of an elbow pipe (unit: mm)

图8 弯管插值点位置Fig.8 Positions of interpolation points of the elbow pipe

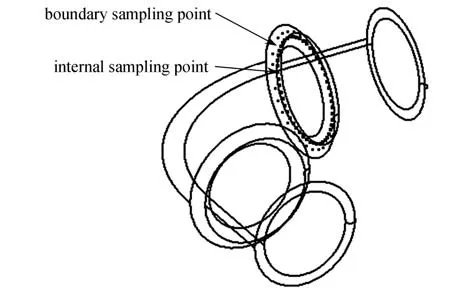
图9 取样点位置Fig.9 Positions of sampling points

弯管的边界条件和位移解析解为

体力项函数分布为

在双互易边界元法中，插值点数量变化对所有节点上面力相对误差和插值稳定性的影响如图10和11 所示.从图中可知，插值点数量增多，所有节点上面力相对误差降低，计算精度提高，其插值稳定性变差.图12和图13分别表示插值点数量为1 961的情况下边界取样点的面力和内部取样点的位移.从图中可以看到，取样点的位移和面力数值解和精确解拟合效果很好，误差小，计算精度高.从图11可以看到，随着插值点的加密，插值矩阵条件数的增长速度越来越缓慢，因此用式(9)控制参数变化是合适的.

图10 边界上面力的相对误差Fig.10 Relative errors of the surface force on the boundary

图11 RBF 矩阵条件数Fig.11 The condition number of the RBF matrix

图12 取样点面力结果Fig.12 Surface force results at sampling points

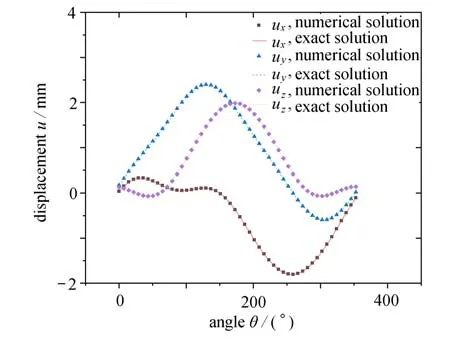
图13 取样点位移结果Fig.13 Displacement results at sampling points

从上述两个具体的双互易边界元算例可以看出，采用式（9）插值方案下，能够较好地控制插值矩阵的条件数，同时能够保证插值的收敛性，并且也可以证明指数型基函数在式（9）形状参数变化方案下，作为双互易边界元方法的RBF 解决静弹性力学非齐次问题的有效性.

3.2.3 工字型结构

考虑实际工况下的解析解不易求得的情况，采用双互易边界元法和有限元法进行对比，进一步验证双互易边界元方法在解决静弹性力学问题的有效性.该算例模型为工程上常见的工字型结构，可以作为横梁支架等应用场景.模型的几何尺寸见图14，材料参数为：Poisson 比0.28，弹性模量2 000 MPa，密度0.007 9 t /mm3.工字型结构的边界条件为：左端面施加压力为100 MPa，右端面固定约束，给定z方向上体力为- 20 N/mm3，约束和载荷如图15所示.

图14 几何尺寸图 (单位：mm)Fig.14 Geometric dimensions (unit: mm)

图15 载荷和约束Fig.15 Loads and constraints

双互易边界元法中，指数型函数作为双互易边界元法中的RBF 并且形状参数方案为式（9），采用线性三角形单元，单元数量为1 656，节点数量为1 108.

有限元法中，采用六面体线性单元类型，如图16，单元数量为4 440，节点数量为5 859.取样点为单元节点位置，如图17所示，坐标如表1所示.

表1 取样点坐标Table 1 Coordinates of sampling points

图16 有限元单元离散Fig.16 Finite element discretization

图17 取样点位置Fig.17 Sampling point positions

图18是双互易边界元双法以及有限元法对工字型结构进行静弹性力学分析得出的取样点位移分量ux，uy和uz.从图18中可以看出，双互易边界元法和有限元法两种方法分析得到的位移数值结果拟合程度较高，进一步说明了指数型基函数作为双互易边界元方法的RBF 对于结构静力学分析的有效性和准确性.

图18 取样点的位移Fig.18 Displacements of sampling points

4 结 论

本文从含有域内项弹性力学边界积分方程出发，运用指数型RBF 对体力项进行插值，分析指数型插值函数的形状参数变化方案下插值点数量对RBF 插值精度和稳定性的影响，并应用到双互易边界元法中分析数值误差.算例表明，在指数型基函数形状参数等于插值点最近距离的最小值插值方案下，控制形状参数能够有效控制插值矩阵条件数的快速增长，同时也能够达到很高的插值精度，其取样点的位移和面力数值解和解析解拟合程度高，并且在无解析解实际工况下双互易边界元法和有限元法数值结果吻合度较好.数值结果说明了指数型基函数在式（9）插值方案下，作为双互易边界元法的RBF 解决静弹性力学中非齐次项问题的有效性，适合求解实际工程中的非齐次问题.