裂纹体分析的权函数理论与应用: 回顾和展望

吴学仁 徐 武

1 北京航空材料研究院, 北京 100095

2 上海交通大学航空航天学院, 上海 200240

1 引 言

在材料制备/构件制造和结构使用过程中, 难以避免出现各种原因引发的裂纹(缺陷/损伤).裂纹在使用载荷/环境因素作用下的持续扩展, 会导致结构的灾难性破坏. 图1 给出了对推动断裂力学和损伤容限设计准则的发展具有“里程碑”意义的结构破坏事故. 自20 世纪中叶开始迅速发展的断裂力学, 为含裂纹材料和结构的安全性评定和使用寿命预测提供了理论和方法, 在航空航天、先进材料、核电能源、石油化工、交通运输、大型装备和土木工程等诸多领域得到了广泛应用. 由于安全系数和使用寿命要求, 含裂纹工程材料和结构基本都使用在线弹性范围(包括小范围屈服). 只要构件承受的载荷不超过其全塑性屈服载荷的50%, 甚至净截面应力不超过80%材料屈服应力(NASGRO 2012), 在通常情况下小范围屈服就是合理的假设. 即使结构件出现塑性屈服, 基于线弹性断裂力学(linear elastic fracture mechanics, LEFM)分析的结果经适当修正后仍然有效. 甚至在进入大范围屈服阶段后, 弹性区部分仍然要用LEFM 的分析方法(黄克智和余寿文 1985). 这使得LEFM 成为含裂纹材料与结构的剩余强度分析和使用寿命预测的主要理论工具.

在线弹性条件下, 主宰裂纹尖端应力应变场奇异性强度的关键力学控制参量是由Irwin(1957)首次提出的应力强度因子K(stress intensity factor, SIF).K包含了裂纹体几何和载荷对裂纹尖端场奇异性强度的影响, 唯一地表征了线弹性裂纹尖端场的强度(Hutchinson 1979, 杨卫1995, 王自强和陈少华 2009). 这使得以K为核心的裂纹尖端场的“单参量表征(one parameter characterization)”成为断裂力学中最重要的概念之一(Anderson 2005). 对于断裂力学的工程应用来说,K为由实验室简单试样的试验结果向复杂工程结构的转移奠定了理论基础. McClung 等(2013) 指出: 在材料和结构的疲劳裂纹扩展寿命分析中,K的计算是最重要的一步. 作为裂纹扩展的驱动力(driving force),K的高精度求解计算是线弹性断裂力学的中心工作(ASTM E08.04.01 2018), 也是损伤容限设计和结构完整性评价的关键和前提.

长期以来, 国际断裂界发展了许多求解K的理论和方法. 但由于裂纹尖端应力场的奇异性,严格的理论解法只限于极少的理想裂纹几何/载荷情况, 如无限大板中心裂纹/周期性共线裂纹,内埋椭圆裂纹, 以及半无限裂纹. 对于工程实际中的绝大多数有限体裂纹几何, 目前采用的两种主要方法则是数值方法(有限元法FEM 和边界元法BEM)和权函数法(weight function method,WFM). 数值方法对复杂裂纹几何体具有强大的分析能力, 但正如负责航空航天结构损伤容限设计大型工业软件开发的美国西南研究院(SwRI) McClung 等 (2013)指出的, FEM 等数值方法分析裂纹问题在技术上固然没有困难, 对一些特殊的现场裂纹问题分析是个很有吸引力的选择. 但对于含有大量断裂关键部位的复杂结构来说, 由于裂纹尖端场的奇异性和裂纹尺寸的不断变化,使得各种数值方法的建模/计算工作量很大, 所以数值方法作为一种通用的结构损伤容限设计工具仍然是不现实的(impractical).

图1推动断裂力学和损伤容限设计准则发展的“里程碑”事故. (a)斯克内克塔迪自由轮在平静的港湾中整体断裂为两段(Tetelman & McEvily 1967), 该事故引起人们对裂纹尖端场的关注与研究;(b) 锻造缺陷引起的裂纹导致美国空军F-111 战斗轰炸机机翼断裂坠毁, 该事故推动了损伤容限设计准则和规范的建立(Wanhill 2003); (c) 多位置损伤MSD 导致阿罗哈航空公司波音737-200机身压力舱上部蒙皮被撕脱,该事故改变了大型运输机的适航规范 (Wanhill 2003, FAA 2010);(d) 疲劳裂纹导致CF6-6D 航空发动机钛合金一级风扇盘破裂, DC-10 客机坠毁(McEvily 2002),它推动了发动机损伤容限设计准则和规范的建立.

与FEM 等数值方法的大量建模/计算相比, 权函数法只需通过一个简单的积分, 就能以高出几个数量级的计算速度, 求得裂纹体在任意复杂载荷条件下的完整K(a)曲线. 权函数法以其高度的普适性、出色的求解效率、准确可靠和便于应用的特点, 在裂纹体分析和损伤容限设计中得到了广泛应用. 在国际航空航天界广泛应用的两个大型工业软件中, 权函数法是计算K(a)的主要方法(NASGRO 2012), 甚至是唯一方法(DARWIN 2008). 在迅速发展的各类新型材料(智能/纳米/生物)裂纹问题的建模分析中, 特别是在桥连增韧方面, 权函数也得到了日益广泛的应用(Shao et al. 2012, Meng et al. 2018, Gao et al. 2021, Wang et al. 2020).

权函数法问世至今已达半个世纪. Bueckner (1970)从各向同性材料的弹性应力场的解析函数性能的角度首次提出了权函数法; Rice (1972)则从应力强度因子与应变能的关系论述了权函数概念, 并提出通过求裂纹面位移对裂纹长度的偏导数获取权函数的方法. 权函数法的独特优势源于把影响裂纹尖端K的两个因素, 即载荷和几何特性进行变量分离. 从理论上说, 权函数本身只代表裂纹体的几何特性(包含力/位移边界的划分)而与裂纹体所受载荷无关(但当前文献中的绝大多数权函数在不同程度上是受到用以推导它们的参考载荷情况影响的, 见3.3 节). 在权函数法的研究与应用中, 各类裂纹几何高精度权函数的推导和验证则是关键.

结合笔者关于权函数法的若干综合性研究工作(Wu & Carlsson 1991, Wu 2019, 吴学仁等2019, Wu & Xu 2022), 本文力图对50 年来国际断裂界在权函数法研究与应用方面取得的主要进展进行历史性回顾, 并对权函数法的未来发展与工程应用作出展望. 本文讨论的主要内容包括:二维裂纹的几种主要解析与数值权函数法, 以格林函数为基准的权函数精度验证, 三维裂纹的片条合成权函数法和点载荷权函数法, 以及权函数法在裂纹体断裂力学分析求解中的各类工程应用简介.

2 二维裂纹问题分析的权函数法

根据Bueckner (1970) 和Rice (1972)的权函数理论, 以及Wu 和Carlsson (1983)的混合边界条件下的广义权函数法, 结合Bueckner (1958)提出的断裂力学叠加原理, 裂纹体在任意载荷情况下的应力强度因子K可通过对该裂纹体的权函数m(α,ξ/α)和无裂纹体在假想裂纹位置的应力σ(ξ)的乘积, 沿裂纹长度a积分得到. 采用无量纲表达形式, 用权函数法计算K(a)的公式为

式中α和ξ分别是无量纲裂纹长度和坐标,α=a/W,ξ=x/W(a和x分别是实际裂纹长度和坐标;W是裂纹体特征尺寸, 按具体裂纹几何自行选择, 一旦选定则在整个分析过程中保持不变). 式(1)表明, 用权函数法对裂纹体进行断裂力学分析计算只需要两个已知条件. 一是裂纹体的权函数m(α,ξ/α); 二是裂纹面应力σ(ξ), 其定义是: 不考虑裂纹的存在, 由作用在裂纹体边界的所有载荷和位移以及内部体积力和内应力在假想裂纹位置引起的应力, 也称为“无裂纹应力”.σ(ξ)的分析计算与裂纹无关, 是一个常规的弹性力学问题, 可用弹性理论和/或有限元等数值方法通过一次计算确定. 所以权函数法的核心是宽范围高精度权函数m(α,ξ/α)的确定与验证.

权函数的推导方法可归为两类: 解析法和数值法. 数值方法不但计算量很大, 而且通常只能给出若干离散点(裂纹长度和位置)的权函数值, 使用不便. 解析方法则能得到作为裂纹长度连续函数的权函数表达式, 使用方便高效. 但不同解析方法所得到的权函数精度水平差异较大, 需要严格验证确认. 解析权函数法一般需要已知参考载荷情况的K解为前提条件. 根据所用的单个或多个参考载荷情况(multiple reference state, MRS)可分为不同的推导方法. 应该指出, 本文所说的解析权函数并非严格的理论精确解(只有极少数裂纹几何存在权函数精确解), 而是采用解析推导方法得到的非精确权函数, 其精度取决于具体推导方法和输入条件.

2.1 基于裂纹张开位移的规范化解析权函数法

Rice (1972)指出, 权函数m(α,ξ/α)可通过参考载荷(用下标r 表示)情况下的裂纹张开位移(COD), 即Ur(a,x), 对裂纹长度a求偏导数得到.

式(2)是基于裂纹张开位移的规范化解析权函数法的基础.

2.1.1 规范化解析权函数的推导

参考载荷情况下的COD 解Ur(a,x)是推导权函数m(α,ξ/α)的前提. 文献中虽然有大量的应力强度因子解, 却鲜有高精度的裂纹COD 解. 这使得有限体裂纹的解析权函数推导成为一个相当棘手(rather formidable)的问题(Sham 1987). Petroski 和Achenbach (1978)提出了利用参考载荷情况的应力强度因子Kr确定COD 的一种有效的P-A 方法, 得到许多研究者的关注和应用.但学者们通过深入研究发现, 这种方法尽管很有效, 但在求解精度和适用范围方面存在一些局限性(Gorner et al. 1985, Fett 1988, Niu & Glinka 1987, Beghini et al. 1991, Wu & Carlsson 1991),主要原因是其COD 表达式只有2 项. 如一些研究者指出(Orange 1985, Fett & Bahr 1999, Karihaloo & Xiao 2003), 用仅含有2 项的表达式很难给出有足够精度的COD, 特别是当裂纹较长时.这使得P-A 方法的应用受到一些限制. 而Orange (1972, 1985)基于圆锥截面的边缘裂纹COD 表达式也只包含2 项, 同样精度偏低(Grandt 1975).

2.1.1.1 裂纹张开位移的确定和验证

为了更合理地表达不同类型裂纹的张开位移, 考虑到边缘裂纹和中心裂纹张开位移的显著差别, Wu 和Carlsson (1991)提出把二维裂纹几何分为两类, 即中心裂纹和边缘裂纹(图2), 对其裂纹张开位移各采用一个规范化的COD 表达式, 并对长度尺寸和应力进行无量纲正则化处理,以使得推导清晰简洁. 无量纲裂纹长度α=a/W, 正则化坐标ξ=x/W. 坐标原点位于裂纹嘴(crack mouth), 如图2 所示.

(1)中心裂纹. 以无限板中心裂纹的COD 解析解为基础, 在整个裂纹面受连续分布应力作用下, COD 假设为以下级数形式(Wu & Carlsson 1991, Wu 1992)

式中的函数Fj(α)采用3 个求解条件确定. 条件1: 裂纹尖端关系, 即裂纹尖端后方(ξ/α→1)处的裂纹张开位移ur(α,ξ)和应力强度因子Kr(a)的关系; 条件2: 自洽性, 即基于“自洽性(self consistency)”原理(Petroski & Achenbach 1978), 把所推导的权函数用于计算参考载荷σr(x)自身作用下的应力强度因子K时, 其结果应当与参考应力强度因子解Kr(a)完全一致; 条件3: 裂纹嘴张开位移(CMOD), 即Vr=ur(α,ξ= 0).

对于最简单的裂纹面均布应力情况(σr(ξ)/σ0= 1), 由以上条件可确定中心裂纹几何的Fj(α)

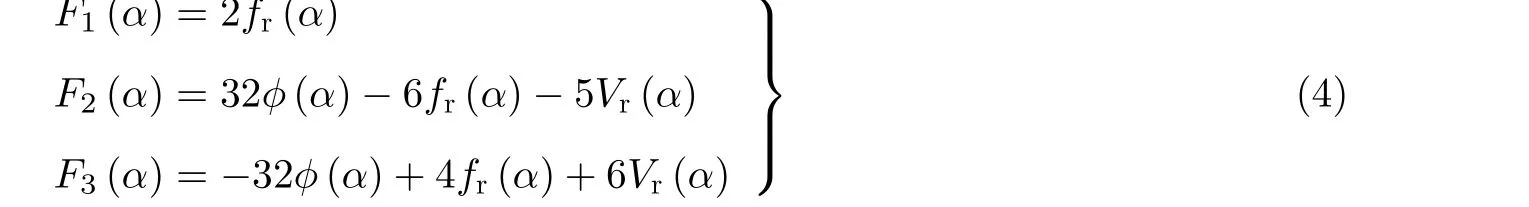
式中:

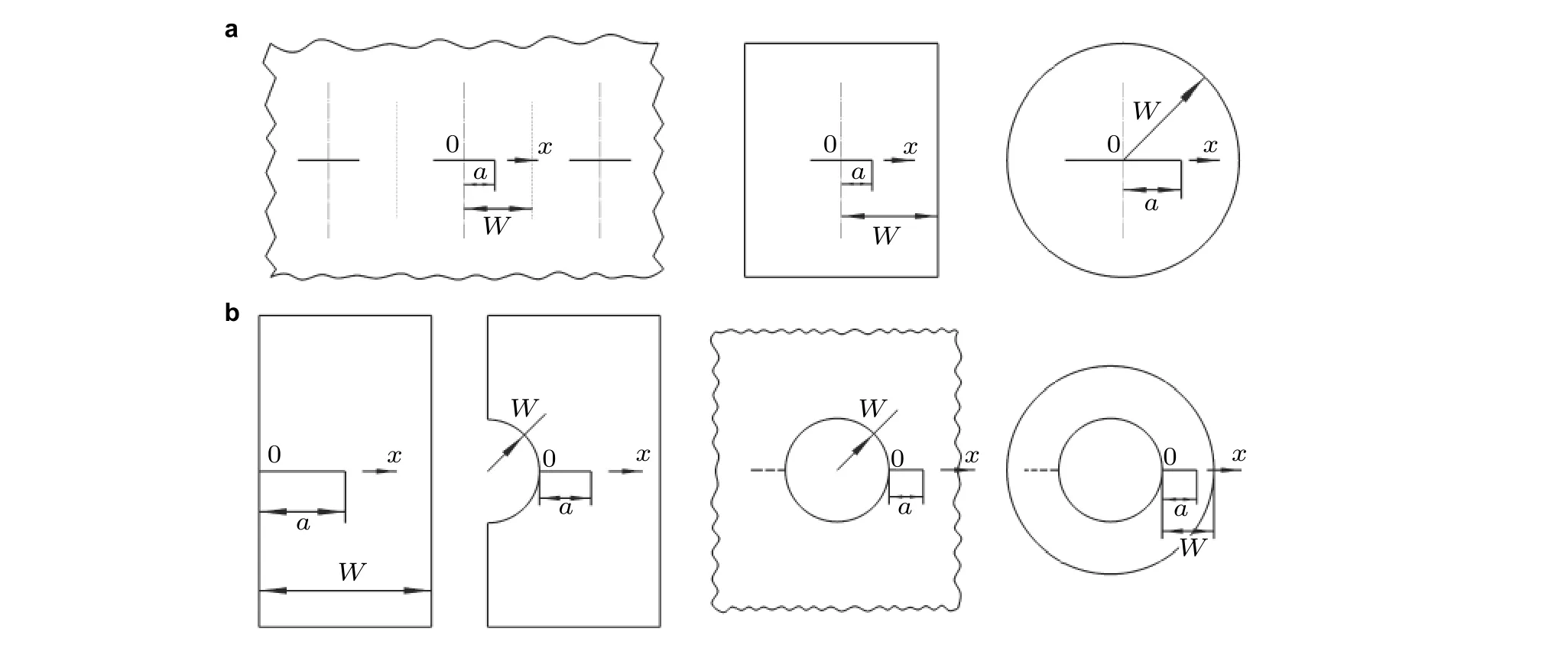
图2裂纹几何分类和特征尺寸W 选取示例. (a)中心裂纹, (b)边缘裂纹. 注意中心裂纹和边缘裂纹对裂纹嘴的定义

为验证式(4)的精度, 考虑唯一有COD 精确解的“有限”(裂纹长度与裂纹间距之比)裂纹几何,即无限板周期性共线裂纹在裂纹面均布应力作用下的COD. 由无量纲应力强度因子fr和裂纹嘴张开位移CMOD 的精确解Vr(Tada et al. 2000)确定Fj(α)函数,进而求得COD. 所得结果与COD 的精确解比较, 二者在α= 0 ～ 0.8 范围内几乎完全一致, 即使在α= 0.9 时最大相对差异也小于0.5%, 见图3(a).

(2)边缘裂纹. 在整个裂纹面受连续分布应力作用下, 有限体边缘裂纹的COD 假设为以下级数形式(Wu & Carlsson 1991, Wu 1992)

式中, 函数Fj(α)一般采用4 个求解条件确定. 前3 个条件与中心裂纹相同, 第4 个条件是: 边缘裂纹COD 廓线的二阶导数在裂纹嘴处(ξ= 0)为0 (Fett et al. 1987, Fett & Munz 1997), 即

对于最简单的裂纹面均布应力情况(σr(ξ)/σ0= 1), 由以上条件可确定边缘裂纹几何的Fj(α)

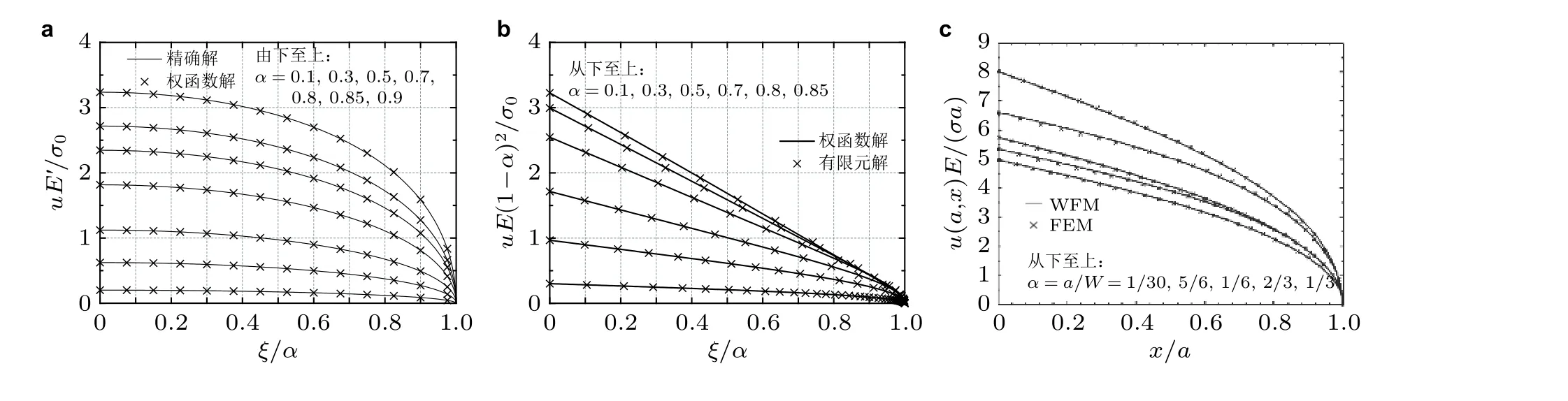
图3三种裂纹几何的COD 权函数解与精确解及有限元解比较. (a) 无限板周期性共线裂纹受裂纹面均匀应力, (b) 圆盘径向边缘裂纹受裂纹面均匀应力, (c) 无限板孔边径向双裂纹受远方拉伸

式中:

为验证边缘裂纹COD 的求解精度, 考虑直径为D的圆盘中的一条径向边缘裂纹, 取D为特征尺寸(α=a/D). 在裂纹面均布应力(σr(ξ)/σ0= 1)作用下, 应力强度因子和裂纹嘴位移的参考解fr(α)和Vr(α)都有理论精确解(Gregory 1977), 据此可确定圆盘边缘裂纹的COD,ur(α,ξ/α).图3(b)是与有限元结果的比较. 二者在α= 0 ～ 0.8 的范围内几乎完全重合, 即使在α= 0.85 的情况下, 差别仍然非常小. 这表明中心裂纹和边缘裂纹在参考载荷为裂纹面均布应力情况下, 求得的裂纹张开位移都有很高的精度. 对非均布应力如多项式分布, 函数Fj(α)的推导可见文献(Wu & Carlsson 1991, 吴学仁等 2019), 其结果精度也高. 以无限板孔边双裂纹为例, 取远方拉伸下的裂纹面非均布应力为参考载荷. 图3(c)是解析权函数法和有限元计算的COD 比较. 可见二者偏差绝大部分都在1%以内, 最大不超过± 1.4%. 这说明采用明显非均布裂纹面应力作为参考载荷, 解析权函数法给出的裂纹面全场位移仍有高精度. 这3 种情况的结果表明, 此方法对参考载荷适应性很强, 能为基于裂纹张开位移的规范化解析权函数推导提供可靠保证.

2.1.1.2 中心裂纹和边缘裂纹的规范化解析权函数

将中心裂纹和边缘裂纹的COD 解析表达式对裂纹长度α求偏导数, 可得到权函数的解析表达式m(α,ξ/α).

(1)中心裂纹

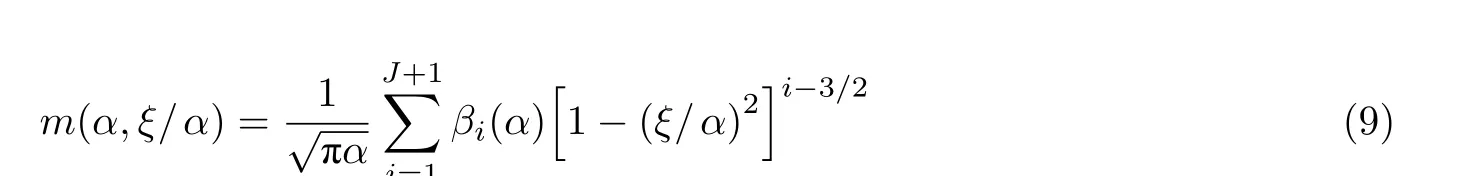
式中, 系数βi(α)可以简写为

其中, 当i= 0 或i≥J时,Fi(α) = 0.

作为示例, 图4(a)给出了无限板周期性共线裂纹的βi(α)曲线. 注意这里讨论的是几何对称的中心裂纹. 偏心裂纹的权函数推导和应力强度因子计算可参阅相关文献(Chen & Albrecht 1994, Ng & Lau 1999, He et al. 2018).

(2)边缘裂纹

式中, 系数βi(α)可简写为

其中, 当i= 0 或i≥J时,Fi(α) = 0.

作为示例, 图4(b)给出了圆盘径向边缘裂纹的βi(α)曲线.

以上用于I 型裂纹的规范化解析权函数的推导方法也适用于Ⅱ型裂纹, 并可推广到各向异性材料的裂纹问题(Xu et al. 2020a, 2020b; 吴学仁等 2019; Wu & Xu 2022). 对于II 型裂纹问题,推导中只需要把I 型参考应力和参考解替换为II 型. Xu 等 (2020a)采用这种方法给出了有限矩形板/圆盘的中心/边缘裂纹, 以及孔边裂纹的II 型权函数(Xu et al. 2018). 对于各向异性材料裂纹问题, 只要在推导中把各向同性材料的应力强度因子和裂纹嘴张开位移CMOD 参考解fr(α)和Vr(α)分别替换成fr(α,ρ)和Vr(α,ρ),ρ为各向异性材料弹性模量和泊松比相关的无量纲参数(Xu et al. 2020b).

2.1.1.3 基本载荷情况下的应力强度因子封闭解

按以上方法得到权函数m(α,ξ/α)后, 与假想裂纹位置处的无裂纹应力σ(ξ) (也称为裂纹面应力)作乘积代入式(1)完成积分, 就得到应力强度因子K(a). 由于m(α,ξ/α)含有奇异项, 有时需要进行数值积分. 处理裂纹尖端ξ/α→1 奇异项的数值积分方法可见文献 (Jones 1998, John et al. 1995, Mawatari & Nelson 2011). 但对于裂纹面多种基本载荷σ(ξ)/σ0情况, 与式(9)和式(11)的规范化解析权函数m(α,ξ/α)的乘积可通过解析积分得到无量纲应力强度因子f(α)的封闭解.因此可把复杂裂纹面应力分解为几种简单基本载荷情况: (a) 集中力; (b) 幂函数分布应力; (c)区段线性应力, 见图5. 利用叠加原理通过简单的四则运算, 快速求得各种复杂应力情况下的K(a).

(1)集中力, 图5(a)

考虑作用在裂纹面ξ处的一对集中力P(单位厚度). 其应力强度因子为

对于中心裂纹

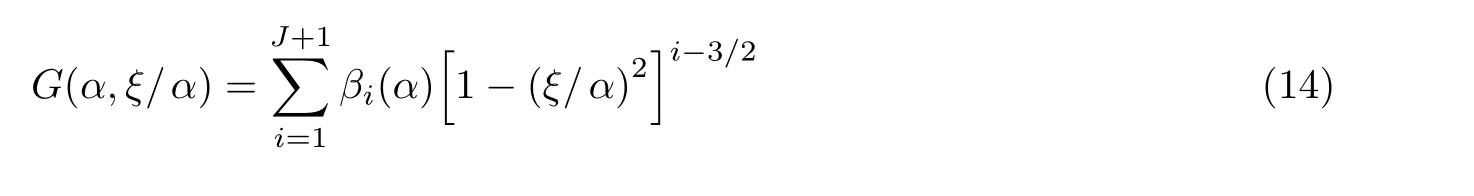
图4无限板周期性共线裂纹和圆盘径向边缘裂纹的βi(α)曲线. (a) 无限板周期性共线裂纹, (b) 圆盘径向边缘裂纹

图5裂纹面的3 种基本载荷情况. (a) 集中力, (b) 幂函数分布应力, (c) 裂纹面区段线性应力

对于边缘裂纹

鉴于式(16)的直接关系, 权函数常被视为与格林函数(也称为影响函数)等效. 本文在对权函数精度作评价时, 把二者视为等同. 作为示例, 图6 给出了2 个代表性裂纹几何的G(α,ξ/α)曲线: (a) 圆盘中心裂纹, (b) 圆盘边缘裂纹. 可见不同裂纹几何的格林函数差别很大.

图6典型裂纹几何的格林函数曲线. (a) 圆盘中心裂纹, α = a/R, (b) 圆盘边缘裂纹, α = a/D

(2)幂函数分布应力, 图5(b)

考虑裂纹面承受幂函数分布应力

对应的无量纲应力强度因子fn为

对于中心裂纹

对于边缘裂纹

利用以上fn值, 可通过简单四则运算得到在裂纹面多项式应力作用下的f和K

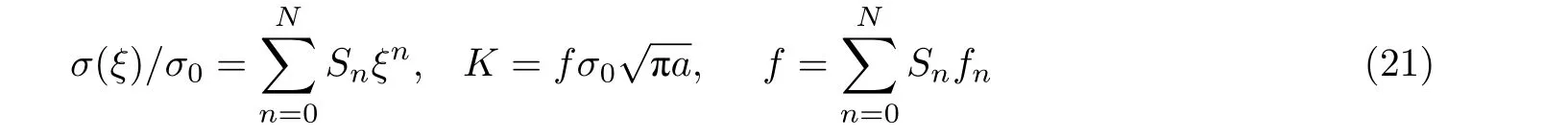
(3)裂纹面任意部分的区段线性应力, 图5(c)

考虑裂纹面任意部分承受区段线性应力

式中fc和fl分别对应于应力的常量和线性部分.

对于中心裂纹

对于边缘裂纹

计算得到每个线性区段的fi值后, 对整个裂纹长度α范围内的所有区段求和, 就能求得整个裂纹面受载下的无量纲应力强度因子f. 这种区段线性化处理的方法与有限元应力分析的输出结果结合, 会使得f的求解十分灵活高效. 它尤其适用于应力变化剧烈难以用多项式拟合的情况,如高梯度热冲击应力和残余应力.

2.1.1.4 共线多裂纹的解析权函数法

运输类飞机结构中存在大量相似细节(如铆钉孔), 在循环载荷作用下, 这些细节处将萌生多条疲劳裂纹. 共线多裂纹/多位置损伤(MSD)是运输类飞机结构中普遍存在的开裂模式, 多裂纹之间相互干扰, 加快疲劳裂纹扩展速率, 其连通将严重降低结构的剩余强度和寿命, 造成灾难性事故(Schijve 1992, Swift 1994, Wanhill 2003). 含MSD 结构的剩余强度和寿命分析是保障飞机结构安全的关键之一, 也是运输类飞机的适航要求(FAA 2010). 尽管有限元等各种数值方法在技术上能解决复杂共线多裂纹结构的疲劳裂纹扩展寿命预测和剩余强度分析的问题, 但共线多裂纹建模繁琐、耗时. 尤其是裂纹长度不断变化的疲劳裂纹扩展分析, 不仅要求不断重新划分网格而导致建模复杂、计算量大, 而且需要很高的建模技术和经验. 近年来, 徐武和合作者在国际上首次建立了针对共线多裂纹的解析权函数法, 推导出多种共线多裂纹几何的权函数精确解, 并得到数值方法的验证和试验结果的支持(徐武2012; Wu & Xu 2022; Xu et al. 2012, 2014; Xu &Wu 2012; Liu et al. 2019), 可为飞机结构的MSD 分析提供一种高效可靠的解析求解途径.

(1) 共线多裂纹权函数法的基本公式

采用Wu 和Carlsson (1983, 1991)提出的载荷-位移混合边界条件下的广义权函数法和Betti 互易定理, 徐武 (2012)和Xu & Wu (2012)提出了载荷-位移混合边界条件下的I 型和II 型共线多裂纹问题的权函数法和相关公式.

以图7 中的两条裂纹为例, 根据叠加原理, 图7(a)载荷下的应力强度因子与图7(b)载荷下的应力强度因子相同. 裂纹受图7(b)所示载荷下裂纹尖端A,B和C的应力强度因子为

图7推导共线裂纹权函数法的叠加原理. (a) 共线裂纹受复杂外载荷, (b) 只有裂纹面受载

式中, 积分区间L=C1∪C2,C1= [0,a],C2= [b,c],a,b和c为裂纹尖端的位置. σ(x)为图7(b)裂纹面载荷, 它等于不含裂纹时图7(a)受载弹性体沿裂纹方向的y向正应力. 裂纹尖端A,B和C的权函数mA(a,b,c,x),mB(a,b,c,x)和mC(a,b,c,x)分别为

通过对比单裂纹和共线裂纹可以看出: 在任意对称载荷下, 单裂纹和共线多裂纹的应力强度因子的权函数法计算公式相同. 一旦确定了某共线多裂纹结构的权函数, 该裂纹体受任意载荷下的应力强度因子便可通过积分确定; 共线多裂纹和单裂纹的区别在于它们的权函数表达式和积分区间不同. 共线多裂纹的权函数是所有裂纹面张开位移的函数, 积分区间包含所有裂纹面, 而单裂纹的权函数只与自身张开位移有关, 积分区间为自身裂纹面.

(2) 共线多裂纹的解析权函数

参考载荷下的应力强度因子和裂纹面张开位移COD 是确定共线多裂纹权函数的前提. 文献(徐武 2012, Xu & Wu 2012, Liu et al. 2019)基于Sih (1964) 给出的共线裂纹受均匀载荷下的复变应力函数, 给出了两条共线裂纹和三条对称共线裂纹的解析权函数. 这里以图8(a)所示3条对称共线裂纹为例, 说明共线裂纹权函数的求解步骤及其特点.

图8(a) 3 条对称共线裂纹, (b) 两条不等长共线裂纹远端受均匀拉伸应力

由Sih (1964)给出的无限宽板3 条对称共线裂纹受双轴拉伸载荷下的复变应力函数, 可以推导出均匀拉伸载荷下的裂纹尖端应力强度因子和裂纹面张开位移

采用分部积分,再用一般的数值积分法便能获得高精度张开位移. 把以上裂纹张开位移和应力强度因子代入(29)中, 得到裂纹尖端A,B和C的权函数. 图9 给出了无限宽板3 条对称共线裂纹的权函数(a= 1,b= 2 和c= 4). 该权函数考虑了裂纹和载荷关于x和y轴的对称性.

基于共线多裂纹的权函数法, Liu 等 (2019)给出了图8(b)所示两条不等长共线裂纹的I 型权函数, 它不要求载荷关于y轴对称. 图10 给出了两条不等长共线裂纹裂纹尖端C和D的权函数. 从图中可看到单裂纹的权函数与共线裂纹权函数的区别, 即共线多裂纹的权函数是由几部分组成的.

2.2 基于多种参考载荷的MRS 解析权函数法

图9三条等长对称共线裂纹的权函数(a = 1, b = 2, c = 4). (a) 裂纹尖端A, (b) 裂纹尖端B, (c) 裂纹尖端C

图10两条不等长裂纹的权函数(a = -9, b = -1, d = 2, c = 0, 0.5, 1.0). (a) 裂纹尖端C, (b) 裂纹尖端D

文献中另一类得到广泛应用的权函数法是基于多个参考载荷情况下的应力强度因子解K直接获取权函数. 其中的两种代表性方法分别由Glinka 和 Shen (1991)与Shen 和 Glinka (1991),以及Fett (1992)与Fett 和 Munz (1997)提出. 与2.1 节的基于单个参考载荷情况下的裂纹面张开位移对裂纹长度求偏导数∂u(x,a)/∂a, 进而获得权函数的“正向”求解方法不同, 这两种方法都是先假设权函数的某种表达式, 再由已知的多个(一般为2 个)参考载荷σri(x)和相应的应力强度因子解Kri(a) (i= 2 或3)结合某个几何条件, 通过求解联立方程组来确定预设权函数级数表达式中的2 ～ 3 个系数, 最终得到权函数. Glinka-Shen 的“通用权函数法(universal weight function method, UWFM)”和Fett-Munz 的“直接调整法(direct adjustment method, DAM)”都属于此类反向求解方法. 所获得的许多结果可分别见Glinka (1996), 以及Fett 和 Munz (1997)与Fett(2008)的研究. 在这些推导中都采用了类似于曲线拟合(curve-fit-like)的方法, 以避开偏导数∂u(x,a)/∂a的计算(Ojdrovic & Petroski 1991, Wagner & Millwater 2012). 与此类似的研究工作还有直接用裂纹面张开位移COD 的偏导数∂u(x,a)/∂a来取代COD 的级数表达, 再基于多个参考解求解联立方程组, 确定∂u(x,a)/∂a中的系数, 进而获得权函数的方法(Ojdrovic & Petroski 1991, Brennan 1994). 这几种方法尽管在推导细节上有所不同, 但在关键环节即以多个参考载荷情况作为已知条件来反求权函数的方面并无实质性区别, 故可统称为“多参考载荷条件(multiple reference states, MRS)权函数法”.

研究者们提出这些MRS 方法的主要目的, 一是因为P-A 方法得到的裂纹张开位移和权函数精度偏低; 二是为了避免求解偏导数∂u(x,a)/∂a. 文献中认为P-A 方法的缺陷主要有: (1) 所得到的裂纹面张开位移的精度不高, 受参考载荷的影响较大, 不适用于明显非均布和不连续的裂纹面参考载荷情况; (2) 权函数的精度取决于裂纹面参考应力σr(x)和所对应的参考应力强度因子Kr; (3) 利用自洽条件所需函数φ(α)的数值积分会显著影响计算效率; (4) 权函数推导计算的工作量大.

以上3 种解析权函数法(Wu-Carlsson, Glinka-Shen, Fett-Munz)需要一个或多个(2 ～ 3 个)参考载荷情况及与其相关的K解(及裂纹嘴位移)作为输入条件. 获得这些信息的途径, 一是从文献中查找理论精确解(非常稀少)或其他解析方法得到的高精度数值解, 二是采用经过验证的高精度数值方法(有限元法、边界元等)计算确定.

下文介绍有关MRS 权函数方法的两个代表性工作, 即Glinka-Shen 的“通用权函数法UWFM”和Fett-Munz 的“直接调整法DAM”, 并对其中值得关注的一些问题作分析讨论.

2.2.1 Glinka-Shen 通用权函数法

Glinka & Shen (1991)比较了文献中的两种权函数表达式(Fett et al. 1987, Sha & Yang 1986)

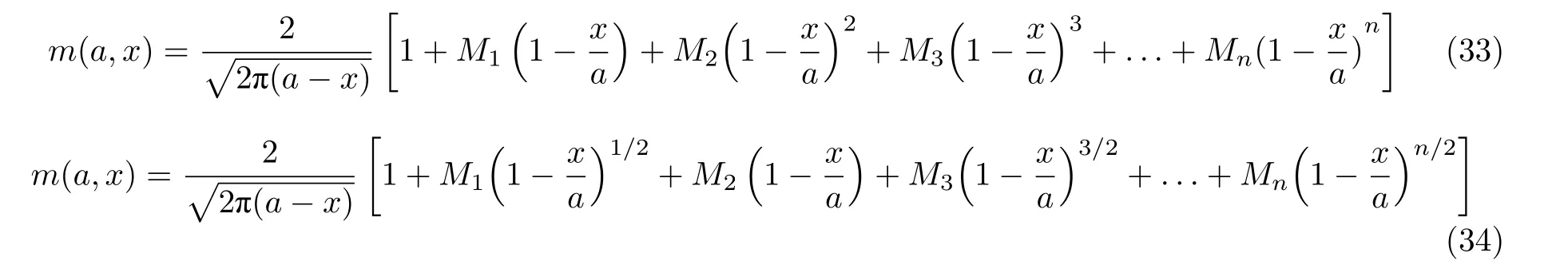
式中n为正整数. 根据拟合结果与以上两种权函数表达式的对比, 认为包含4 项的式(34)权函数的通用性和精度更好. 此式把权函数的推导简化为求解3 个系数(M1,M2,M3)的问题. 所以只要知道2 ～ 3 个参考载荷情况及与之对应的应力强度因子解, 就能直接得到权函数. 解决这个问题有两种途径: (1) 采用3 种参考应力情况及其应力强度因子; (2) 采用2 种参考应力情况及其应力强度因子, 并附加裂纹嘴处的某个几何条件. 以厚壁圆筒径向裂纹为例, 采用3 种参考应力分布σri(x) (均布、线性、二次曲线)及相应的应力强度因子Kri(i= 0,1,2) (Andrasic & Parker 1984),解联立方程组, 确定系数M1,M2和M3, 得到通用权函数m(a,x).

Glinka 和Shen (1991)利用所确定的m(a,x), 计算了4 种幂函数应力分布下(x/B)n,n= 3 ～6 的应力强度因子. 结果与Andrasic 和 Parker (1984)的研究数据符合良好. 据此即认为这些m(a,x)得到了验证. 但应该注意: 所比较的是应力强度因子K而不是权函数m(a,x)或格林函数, 这种比较并不能揭示权函数的真实精度, 见3.1 节.

对于大多数裂纹几何, 获取3 种参考应力下的应力强度因子并不现实. 因此Glinka-Shen 通常采用第2 种方法, 即利用两种参考应力情况及其应力强度因子, 另加裂纹嘴处的某个几何条件, 通过求解联立方程组, 确定权函数的系数M1,M2和M3.

条件1 和条件2 是两种参考载荷情况及其应力强度因子

推导中对中心裂纹和边缘裂纹两种裂纹几何采用了同一个权函数表达式,即式(34). 但这种做法并不合理. Wu 和Carlsson (1991), Fett 和Munz (1997)对这两种裂纹几何是区分的.

关于Glinka-Shen 通用权函数法, 以下两个问题值得关注.

(1) 权函数级数基本项的幂指数不合理

式(34)中的幂指数是(1 -x/a)n/2. 而其他学者, 如Bueckner (1971), Wigglesworth (1957),Wu 和 Carlsson (1991), Fett 和 Munz (1997)采用的都是(1 -x/a)n+1/2. Fett 和 Munz (1997)对这个问题作了深入研究. 结果表明, 边缘裂纹张开位移COD 的级数表达式的幂指数只能是n+1/2, 而n/2 不符合弹性力学理论. 这个差别看似细小, 但却给求解联立方程得到的两种MRS 权函数带来了显著不同(在其他条件都相同的情况下).

(2) 几何条件的选择及其合理性问题

还应注意到的是, Glinka 和Shen (1991)以及Glinka (1996)给出的多种裂纹几何的权函数,实际上是对文献中已有权函数结果的直接拟合, 即是对已有权函数的另一种近似表达. 而不是采用其通用权函数方法推导得到的. 类似的例子还有如: Kumar 和Barai (2010a, 2010b, 2011)对Tada 等(1973)手册中有限宽板边缘裂纹的格林函数拟合得到的权函数表达式. 而Tada 等 (1973)手册中给出的这个格林函数的误差很大, 具体可见3.2 节, 以及Wu 等 (2018a)和吴学仁等(2019). 所以在使用这类拟合的权函数时应倍加谨慎.

2.2.2 Fett-Munz 直接调整权函数法

Fett (1992), Fett 和Munz (1997)提出了采用两个参考载荷情况的K解来确定权函数的直接调整法(direct adjustment method, DAM)法.

边缘裂纹

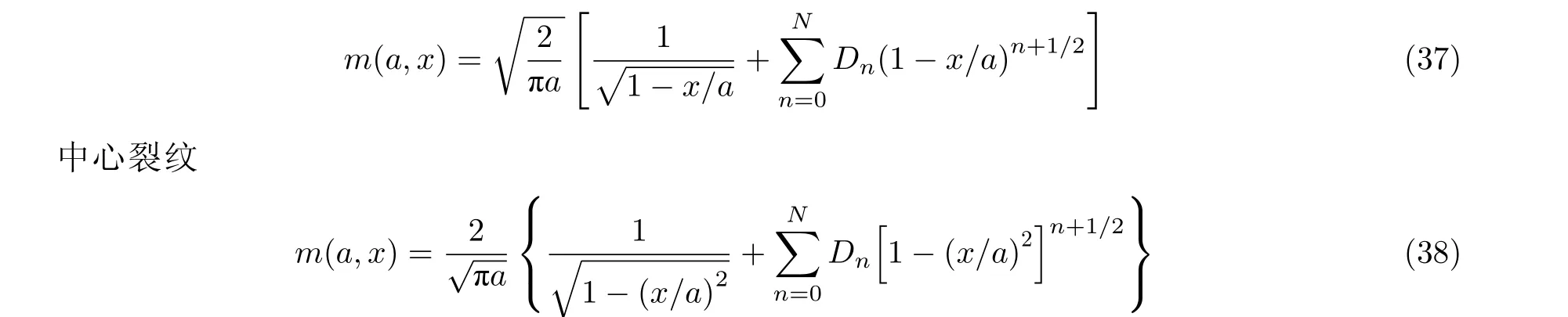
为确定权函数系数Dn, 需要求解由已知参考载荷情况和裂纹嘴位移的一个几何条件组合得到的联立方程组. 如果已知N个参考载荷情况, 则权函数必须满足N+1 个方程.

边缘裂纹

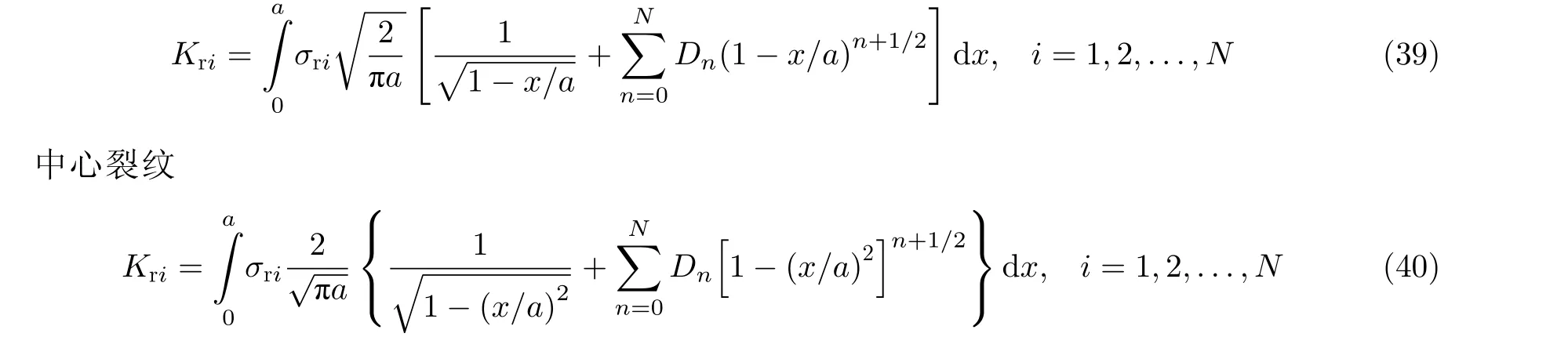
对于中心裂纹, 式(38)自动满足裂纹面位移在裂纹嘴处一阶导数为零的条件. 对于边缘裂纹, 裂纹面位移在裂纹嘴处二阶导数为零(Fett et al. 1987, Fett 1992, Fett & Munz 1997):

解以上联立方程组, 就能确定DAM 权函数m(a,x)的Dn系数.

以上两种MRS 权函数方法在总体思路上是相同的. 所不同的是权函数的级数展开式的幂次: Fett-Munz 采用的(n+ 1/2)与Wu-Carlsson 一致; Glinka-Shen 则采用了n/2. 这个细节区别会导致两种权函数的显著差别.

关于DAM 直接调整权函数法, 有两个问题值得注意.

(1) 边缘裂纹a/W趋于0 时权函数方程组出现病态(ill-conditioned) (Fett 1992, 2008).

例如, 对于有限宽板单边缘裂纹, 如果采用拉伸和弯曲这两种情况作为参考载荷, 则由于它们的无量纲应力强度因子Ft和Fb在a/W趋于0 时都趋于相同的值1.121 5, 使得联立方程中的(Ft-Fb)成为一个趋于0 的微小数值, 它与一个很大的系数相乘, 必将导致明显的舍入误差, 而且(Ft-Fb)还对Ft和Fb值的细微变化十分敏感, 见3.3 节. Fett (1992)对此建议把DAM 权函数的应用范围限于a/W≥ 0.2; 或当a/W趋于0 时不采用DAM 方法, 而只用一种参考载荷(均布应力)的P-A 方法, 结合几何条件mJJ(x= 0) = 0 来确定权函数. 这可能也是Fett-Munz 的权函数在有些情况下只给出了a/W≥ 0.2 的Dn系数值的主要原因. 但如果对不同裂纹长度采用两种不同的权函数法, 其实际操作以及在分界点的衔接会出现问题. 鉴于疲劳裂纹扩展寿命主要消耗在小裂纹阶段,a/W＜ 0.2 的低精度问题是DAM 权函数法的一个明显缺陷.

(2) 几何条件mJJ(x= 0) = 0 的应用缺乏一致性.

文献(Fett & Bahr 1999, Fett 2008, Fett et al. 2000a)给出了两种DAM 权函数结果, 即系数D0,D1和D0,D1,D2, 但对于这个几何条件的利弊作用没有给出量化评估. 图11 显示有限宽板单边缘裂纹是否采用此几何条件的差别(参考载荷为拉伸和弯曲). 尽管对于这个特定裂纹几何和载荷组合, 相对差别不大(1.2% ～ 2.7%), 但对于其他裂纹几何和参考载荷, 差别可能变大.

2.3 获取二维权函数的数值方法

2.3.1 有限元和边界元法

以FEM 和BEM 为代表的各种数值方法在裂纹问题的分析计算中有广泛应用. 这些数值方法主要是用来求解应力强度因子, 但也可用于获取权函数. Andrasic 和Parker (1980, 1984)最早提出了一种推导权函数的数值方法-修正映射配位法(modified mapping collocation, MMC), 并用三次样条函数拟合得出曲梁和空心圆筒边缘裂纹的权函数. Sham (1987)提出了获得二维和三维权函数的统一的FEM 数值解法. Tsai 和 Ma (1989)利用FEM 和虚拟裂纹扩展(virtual crack extension, VCE), 并结合最小二乘法拟合得到了离散节点的权函数. 为避免采用裂纹尖端奇异性单元, Beghini 等 (1991)提出一种了基于粗网格FEM 的权函数推导方法, 但其求解精度明显偏低(7%). Lee 和Hong (1995)采用间接边界积分法(indirect boundary integral method)求得了7种裂纹几何的权函数, 由此计算的5 种幂函数应力(σ(ξ)/σ0=ξn,n= 1 ～ 5)下的应力强度因子与Wu 和Carlsson (1991)权函数法给出的结果高度一致. Fett (1997)用边界配位法(boundary collocation method, BCM)得到了圆盘边缘裂纹的高精度权函数, 但这种方法不适用于处理短裂纹(a/W＜ 0.2)问题. Xiao 和 Karihaloo (2002), 以及Karihaloo 和 Xiao (2003)用BCM 和离散点最小二乘法(PLS)给出了有限板边缘裂纹的格林函数, 但其系数表达式多达50 个, 使用不便且精度不高. Fett 等 (2004) 通过对FEM 得到的集中力作用下的应力强度因子的拟合, 确定了折线形边缘裂纹的权函数. Deng 和Matsumoto (2017)采用类似方法通过拟合集中力加载下的FEM/VCE 结果, 得到了剪切梁边缘裂纹的权函数, 但此方法所需工作量很大. Kuna (2013)的近期专著对有限元法用于权函数的求解作了专题介绍. 另一种常用的数值方法是边界元法(Aliabadi et al.1987). Lorenzo 等 (1994) 把BEM 与Bueckner 奇异场的减除相结合, 推导出几种边缘裂纹的标准形式权函数, 用于裂纹张开位移和条带屈服模型分析, 所得结果与Wu-Carlsson(1991)的权函数解符合得很好. Ince (2012a, 2012b)利用BEM 给出了多种楔形拉伸试样的高精度权函数及其拟合公式. 更多关于数值权函数法的研究工作可查阅相关文献.

图11几何条件m′(x = 0) = 0 采用与否对有限宽板单边缘裂纹权函数的影响. (Wu 2019, 吴学仁等 2019)

总体上看, 数值解法的主要优势是处理复杂裂纹体几何构型的能力. 其不足之处一是一次建模计算只能处理一个裂纹尺寸, 如要获取许多裂纹尺寸的权函数, 则建模计算工作量很大; 二是短裂纹的求解精度很难保证; 三是通常只能给出离散点的权函数值而不是解析表达式, 使用不便. 所以用数值方法获取权函数不太可取, 但数值方法对于各种解析权函数的精度评价和验证能发挥重要作用.

数值方法对复杂裂纹体分析有强大能力, 但由于裂纹尖端应力应变场的奇异性, 裂纹体分析的数值建模和计算远比无裂纹体复杂, 且一次建模计算只能得到一个裂纹长度a在一种载荷条件下的K值. 而疲劳裂纹扩展分析和寿命预测需要从初始裂纹长度a0到临界裂纹长度ac的完整K(a)曲线, 其重复性数值建模和计算对资源的需求很大. 在裂纹体的FEM 分析中, 还需在裂纹尖端区采用密集网格/特殊单元以处理裂纹尖端的奇异性, 并要求分析计算人员具有丰富经验. 而且由于疲劳裂纹寿命主要消耗在裂纹尺寸较小的阶段, 高精度处理小裂纹问题对于FEM建模计算也有很大挑战.

2.3.2 复变函数泰勒级数展开权函数法(WCTSE)

Wagner 和Millwater(2012)提出了一种基于复变函数泰勒级数展开的权函数法(weight function complex taylor series expansion, WCTSE). 与上述求解权函数/格林函数的数值方法显著不同, WCTSE 法采用复变函数泰勒级数展开理论, 结合复变有限元的数值计算结果, 拟合得到给定离散裂纹长度α值的权函数. Jing 和Wu (2015)采用更合理的中心裂纹和边缘裂纹权函数表达式, 进一步提高了WCTSE 权函数的精度; 并用几种典型裂纹几何的已知精确/高精度格林函数进行了验证. 结果表明WCTSE 权函数结果与精确解/高精度解的偏差不超过0.5%.

WCTSE 法是一种把权函数与复变函数有限元法结合的数值方法. 它通过复变有限元法计算裂纹张开位移对裂纹长度的偏导数, 进而获得给定α值的二维裂纹几何的权函数数值解. 其理论基础是Lyness 和Moler (1967)提出的复变函数泰勒级数展开(CTSE)理论. CTSE 是一种概念上与有限差分法类似的数值微分方法, 它利用实轴和虚轴在复平面的正交性求一阶导数. Wagner 和Millwater (2012)将CTSE 首次成功应用于二维裂纹权函数求解, 并与Wu 和Carlsson(1991)的多种裂纹几何的解析权函数结果作了广泛对比. 二者符合得很好.

根据Rice (1972)提出的权函数m(a,x) 与裂纹张开位移对裂纹长度的偏导数的关系

但 采用 常 规 有 限 元 法 计 算∂u/∂a不 仅 操 作 繁 琐, 而 且 很 难 确 定δa的 最 佳 取 值. Wagner 和Millwater (2012)提出采用复变函数泰勒级数展开(complex Taylor series expansion, CTSE)理论取代上式计算∂u/∂a, 解决了δa的最佳取值难题. Jing 和Wu (2015)采用Wu 和Carlsson (1991)的权函数级数展开式对求得的偏导数∂u/∂a作拟合, 分别确定中心裂纹和边缘裂纹的权函数系数Mi. 该方法的细节可参阅Wagner 和Millwater (2012), Jing 和Wu (2015), 以及吴学仁等(2019)的研究.

对于中心裂纹

为验证WCTSE 权函数法的求解精度, 图12 给出了两种裂纹几何的格林函数(与权函数等效, 见下节)与已知解的逐点比较: WCTSE 权函数的两个结果分别与文献中无限板共线裂纹的精确解(Tada et al. 2000)和有限板边缘裂纹的高精度积分方程解(Kaya & Erdogan 1980)高度一致. 在α= 0.1 ～ 0.9,α/ξ= 0 ～ 1 范围内的最大偏差, 前者为0.06%, 后者为0.3%. 与边缘裂纹ξ/α= 0, 0.5, 0.9 的有限元计算结果也符合得很好, 见图12.

为排除在复变有限元计算载中, 不同的载荷施加方式对结果可能产生的影响, Jing 和Wu(2015) 对WCTSE 的载荷无关性作了验证. 结果表明: 无限大板周期性共线裂纹和有限板单边缘裂纹分别在远方均匀拉伸和裂纹嘴集中力两种载荷情况下, 所得到的两组WCTSE 权函数完全一致; 吴学仁等(2019)进而对图13 的 3 种裂纹几何在不同加载条件下求得的Mi系数作了比较,它们的最大差异分别为: 圆盘中心裂纹-0.03%; 三角形板边缘裂纹0.34%; 有限宽板中心孔边裂纹-0.11%. 这些比较进一步验证了WCTSE 权函数法的精度及其载荷无关性.

图12由WCTSE 方法得到的格林函数与无限板周期性共线裂纹精确解以及有限板边缘裂纹积分方程解的比较. (a) 无限板周期性共线裂纹, (b) 有限板边缘裂纹

图13 WCTSE 权函数与复变有限元计算中的载荷无关性检验: 3 种裂纹几何, 各受2 种加载方式.

WCTSE 权函数法的求解精度和效率明显优于有限元法, 其可靠性已得到广泛验证. 但与其他数值方法一样, 它只能给出给定离散裂纹长度α值的权函数; 并且由于网格建模的原因, 处理小裂纹(α＜ 0.1)有困难. 尽管使用方便性不如解析权函数, 但WCTSE 权函数法的宽范围、高精度特点和处理任意裂纹体几何构型的能力, 使其成为评价验证各种解析权函数精度的理想手段.在近期发表的权函数专著中(吴学仁等 2019, Wu & Xu 2022), 就主要是以WCTSE 权函数法的数值解为基准, 对各种解析权函数的精度作广泛验证. 验证示例见第3 节.

3 二维解析权函数的精度评价与讨论

高精度的应力强度因子K是断裂力学分析和结构完整性评定的前提. 权函数法作为求解裂纹体关键力学参量的一种主要方法, 在裂纹问题的分析计算中起着类似于工作母机的作用, 它应具有高精度求解复杂多变载荷条件下的裂纹问题的能力. 为保证权函数法在裂纹体任意载荷条件下都能给出高精度的K和COD 结果, 关键是要确保权函数m(α,ξ/α)自身的高精度. 为此需要严谨规范的评价验证方法和工具. 而选择科学合理的评价基准, 则是对权函数本征精度进行评价验证(verification and validation, V&V)的首要问题.

3.1 权函数精度评价的基准-格林函数

采用权函数法计算裂纹面在各种应力σ(ξ)分布下的应力强度因子K, 并与文献公认或其他方法(如有限元法)得到的高精度K解比较, 是文献中评价权函数精度的一种常用做法. 尽管这种基于比较某些特定载荷情况K的方法对评价权函数精度有一定的参考价值, 但它存在着明显弊端. 因为仅对某些载荷情况下的K值比较, 并不能真实全面地反映权函数自身的本征精度. 由于K值是权函数m(α,ξ/α)和裂纹面应力σ(ξ)的乘积在裂纹长度α范围内的积分结果, 它必然会受m(α,ξ/α)和σ(ξ)的共同影响, 而m(α,ξ/α)本身的误差会因积分的平均效应相互抵消. 故K值的精度与m(α,ξ/α)的精度既有联系又有本质区别. 所以高精度的K值结果不能作为证明高精度m(α,ξ/α)的充分条件. 同一个m(α,ξ/α)在某些载荷情况下能给出高精度K值, 并不能保证在其他载荷情况下也能给出高精度K值. 权函数m(α,ξ/α)是含有两个变量的曲面, 与所受载荷σ(ξ)无关. 而无量纲应力强度因子f(α)则是一条曲线, 且与σ(ξ)密切相关. 二者没有直接可比性.所以用某些载荷情况下的K值比较来评价权函数的精度容易造成假象和误导.

图14 是用同一个权函数(Jin et al. 2017), 采用Glinka-Shen 的UWF 权函数法推导, 参考载荷为双向拉伸, 几何条件为m′(α,ξ/α) = 0)计算得到的无限大板圆孔边径向单裂纹在两种载荷情况下的应力强度因子K与其他方法结果的比较. 图14(a)的载荷是双向拉伸, Jin 等 (2017)的权函数结果与边界配位法(BC)结果高度重合. 图14(b)的载荷是裂纹嘴集中力, 其权函数结果(虚线)却与其他3 种方法的结果(实线和2 种符号)大相径庭(Wu et al. 2018b). 这表明把K值作为验证权函数的基准很容易给出误导性评价结论.

准确反映权函数m(α,ξ/α)本征精度水平的唯一正确途径, 是对裂纹面任意位置ξ/α的权函数精度进行逐点评价(Wu & Carlsson 1991, Wu 1992, 吴学仁等 2019, Wu & Xu 2022). 实现这种逐点评价的最佳基准是格林函数G(α,ξ/α) (Green’s function), 也称为影响函数(influence function). 在数学物理方法中, 格林函数是指点源产生的场, 它表示一个点源在给定边界条件下所产生的场或影响. 对于裂纹问题, 这个点源是指作用在裂纹面任意位置的一对单位集中力P;所产生的场则是在给定裂纹几何及边界条件划分下, 由P(单位厚度)引起的无量纲应力强度因子K, 即格林函数G(α,ξ/α).

与受裂纹面应力分布和积分平均效应明显影响的应力强度因子K(a)不同, 格林函数与这些因素无关. 它代表的是给定裂纹体几何和边界条件划分的本征性能, 因此能客观真实地对权函数的本征精度作出逐点检验. 而格林函数G(α,ξ/α)与权函数m(α,ξ/α)密切相关, 文献中通常视二者为等效. 其唯一差别是一个系数σri.

图14无限板孔边径向单裂纹, 用Jin 等 (2017)权函数计算得到的两种载荷下的K 值与其他方法的比较.

根据上式把m(α,ξ/α)直接转换成G(α,ξ/α)来评价权函数的精度, 不受所考虑的裂纹面应力σ(ξ)的影响, 没有积分平均效应, 不会引入其他误差. 这使得格林函数G(α,ξ/α)成为评价验证权函数m(α,ξ/α)精度的理想基准(Wu & Carlsson 1991, 吴学仁等 2019, Wu & Xu 2022).

用格林函数来评价孔边裂纹权函数的结果示于图15. 两种格林函数分别来自于Jin 等(2017)与Shivakumar 和Forman (1980), 可见二者差别十分明显, 而后者的精度已得到WCTSE的验证(赵晓辰等 2018, 吴学仁等 2019). 在α=a/R= 0.01 ～ 2.0 范围内, 二者相对差别高达±180%; 且Jin et al. (2017)的部分曲线(α=a/R= 0.01 和0.1)甚至出现了负值, 这在物理上是不可能的. 此例表明, 唯有采用格林函数作为评价基准, 方能全面真实地揭示权函数的本征精度.

用于检验权函数精度的G(α,ξ/α)应尽可能用完全独立的其他方法得到. 最方便的方法是用有限元法, 对几个α和ξ/α组合的离散点加集中力P, 计算其K值再转换成G(α,ξ/α), 并把它们与解析权函数通过式(45)转化得到的G(α,ξ/α)作比较. 上文介绍的基于复变函数泰勒级数展开理论的WCTSE 权函数法, 克服了传统有限元法一次计算只能得到一个点的G(α,ξ/α)值的缺陷.它不但能在一次计算中得到给定无量纲裂纹长度α的一条G(α,ξ/α)曲线, 而且其高精度已得到广泛验证, 能为各种解析权函数的精度评价提供理想的验证基准.

如果采用未经格林函数验证的权函数求解裂纹问题, 则所得结果的正确性难以保证, 尤其是在载荷情况与推导权函数所用的参考载荷偏离较大时.

3.2 解析权函数的精度比较与评价

3.2.1 I 型裂纹三种解析权函数的精度比较与评价

以经过严格验证的格林函数为基准, 对3 种解析权函数的精度进行逐点比较评价. 选取3 种代表性边缘裂纹几何, 如图16 所示.

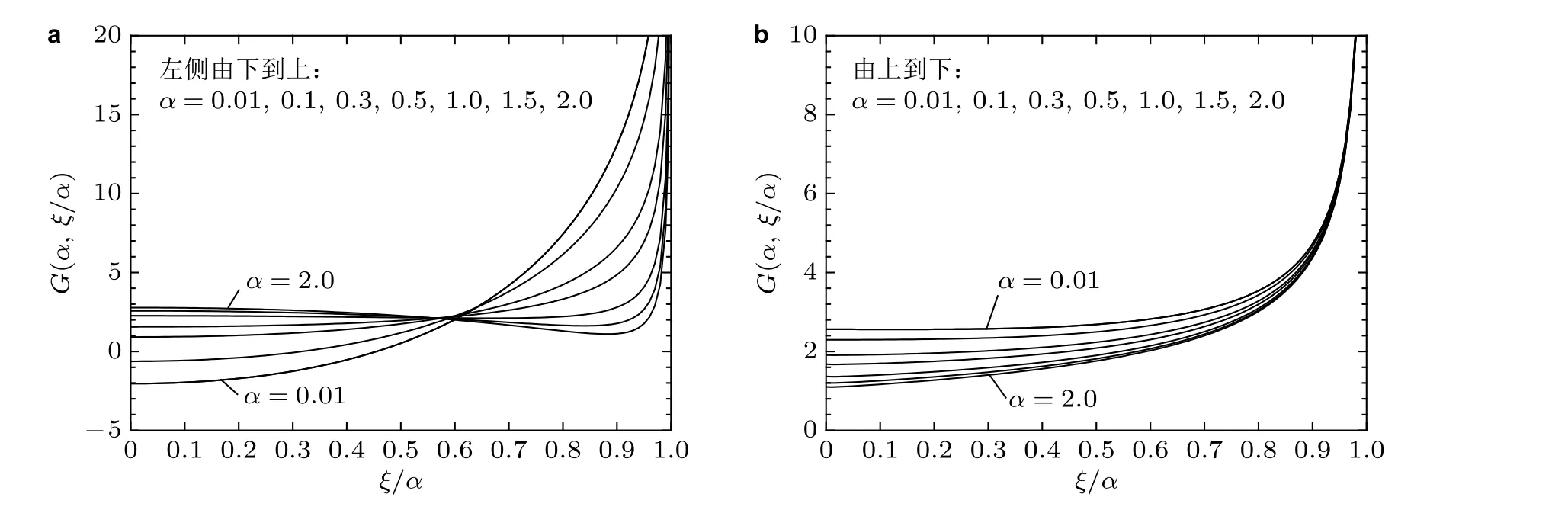
图15无限孔边径向单裂纹的两种格林函数. (a) Jin et al. (2017), (b) Shivakumar & Forman (1980)

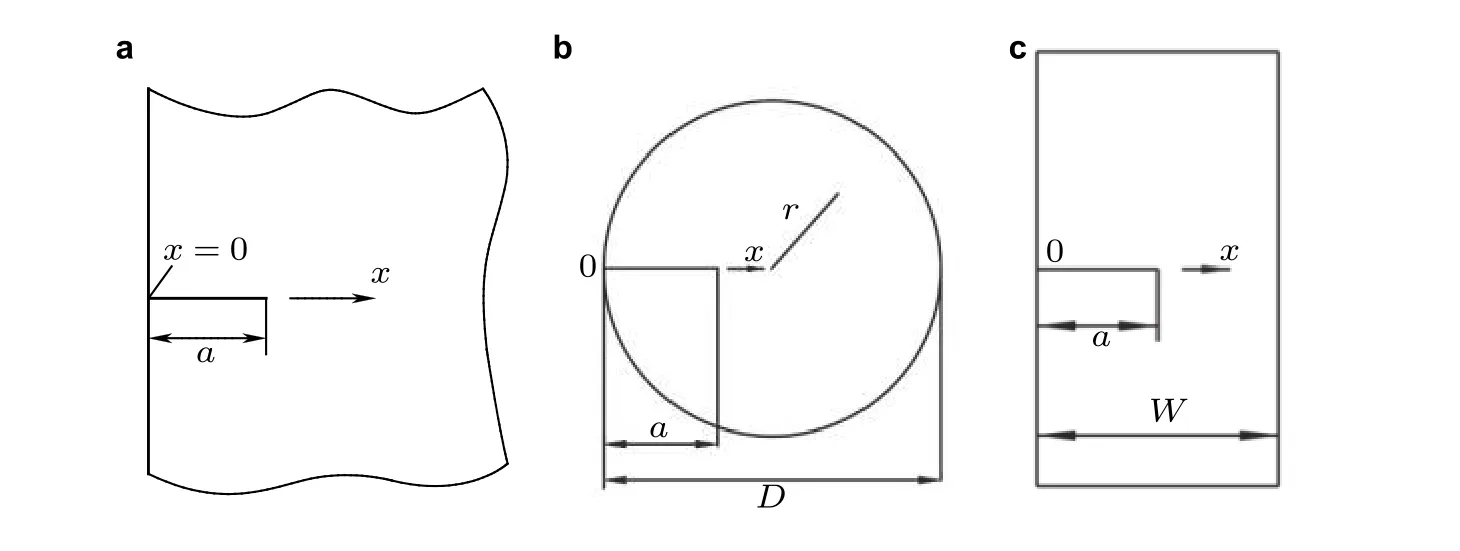
图16评价三种解析权函数精度的三种裂纹几何. (a) 半无限板边缘裂纹, (b) 圆盘边缘裂纹, (c) 有限宽板边裂纹

(1) 半无限板边缘裂纹

考虑半无限板边缘裂纹几何. 以裂纹长度a作为特征尺寸W, 则无量纲裂纹长度α=a/W= 1.图17 是半无限板边缘裂纹的9 种格林函数与Wigglesworth (1957)准精确解, 即式(46)的比较.可见Glinka 和 Shen (1991)的两种格林函数误差最大, 为-9% ～ 6%. 用Petroski 和 Acenbach(1978)得到的权函数偏差局部超过2%. 其他6 种权函数的偏差均在2%以内(吴学仁等 2019).

(2) 圆盘单边缘裂纹

圆盘单边缘裂纹可能是唯一有3 种载荷情况K精确解的特殊有限体裂纹几何. 利用这些精确解(Gregory 1977, 1979, 1989)推导权函数, 能排除参考解误差的影响, 所以能真实反映各种解析权函数方法对于有限单连体边缘裂纹能够达到的最高精度水平. Wu 和Tong 等 (2018a)对这个裂纹几何的各种解析权函数的精度作了系统的评价比较.

图17半无限板边缘裂纹的各种格林函数与Wigglesworth (1957)准精确解的比较(吴学仁等 2019)

基于裂纹面位移的Wu-Carlsson 解析权函数只需一种参考载荷情况(裂纹面均布应力)的Kr和裂纹嘴位移Vr. 图18 是该权函数与WCTSE 权函数的比较曲线. 在α=a/D= 0 ～ 0.7 范围内, 二者最大差别小于0.5%;α= 0.8 和0.85 时, 最大差别分别为1.97%和3.71%, 均在格林函数曲线的最低处(裂纹尖端后方)附近(图18(b)).

两种基于多个参考载荷的MRS 权函数法, 即Glinka-Shen 的通用权函数和Fett-Munz 的DAM 权函数, 采用的2 个参考载荷(均布和抛物线分布)下的K均为Gregory 的精确解. 其格林函数与WCTSE 的比较见图19. 可见即使采用的2 个参考解均为精确解, 得到的权函数精度仍偏低. 这是MRS 权函数法的自身缺陷导致的. 有关讨论见吴学仁等(2019).

(3) 有限宽板单边缘裂纹

Wu 等(2018a)和吴学仁等(2019)对有限宽板单边缘裂纹的各种解析权函数与WCTSE 的结果做了详细比较, 见图20. Bueckner (1971)的权函数给出的有效范围为α=a/W= 0 ～ 0.5,其余3 种权函数的范围为α=a/W= 0 ～ 0.85. 可见 Wu-Carlsson 权函数与WCTSE 的偏差明显小于两种MRS 权函数(均基于拉伸和弯曲2 个参考载荷), 即Glinka-Shen 的通用权函数和Fett-Munz 的DAM 权函数. 注意, 作为极限情况的α= 0.001, 不是与WCTSE 结果的比较, 而是与半无限板边缘裂纹的准精确解式(46) (Wigglesworth 1957)的比较.

有限宽板单边缘裂纹是最常见的裂纹几何之一.其权函数/格林函数应用十分广泛.著名的Tada-Paris-Irwin 应力强度因子手册(Tada et al. 1973, 1985, 2000)被许多研究者广为采用. Tada et al. (1973)手册给出的格林函数公式为 (其注明精度为2%)被许多研究者广泛采用的版本Tada-Paris-Irwin (1973), 即式(47), 偏差更大, 故精度有问题.1985 年后的更新公式(48)在α= 0 ～ 0.7 范围内有明显改进, 但α= 0.8 ～ 0.9 在近裂纹尖端区仍有较大误差.

图18圆盘单边缘裂纹.(a) 两种格林函数 Wu-Carlsson 和WCTSE, (b) 两种格林函数的相对差别

图19圆盘单边缘裂纹两种格林函数的比较. (a) Fett-Munz 与WCTSE, (b) Glinka-Shen 与WCTSE

图20有限宽板单边缘裂纹4 种格林函数与WCTSE 的比较. (a) Bueckner 与WCTSE, (b) Wu-Carlsson 与WCTSE, (c) Fett-Munz 与WCTSE, (d) Glinka-Shen 与WCTSE

图21 是有限宽板单边缘裂纹Tada-Paris-Irwin 公式(47)和(48)与WCTSE 格林函数的比较 (注: 此WCTSE 格林函数的精度已在图12 (b)中得到了验证), 可见二者有显著差别. 特别是

一些研究者为便于解析积分, 把式(47)的格林函数式拟合成另外的形式. Kumar 和Barai(2010a, 2010b, 2011)拟合给出的有限宽板单边缘裂纹的通用格林函数表达式为

式中Mn为拟合系数. 式(49)常被用于该裂纹几何乃至其他相近裂纹体的各种模型分析, 特别是在混凝土断裂方面的相关文献中. 鉴于该式的拟合基础, 即式(47), 存在明显问题, 由此得到的计算结果需谨慎对待.

3.2.2 II 型和各向异性材料裂纹权函数的精度评价

图21 Tada-Paris-Irwin 手册(1973, 1985, 2000)的有限宽板单边缘裂纹格林函数与WCTSE 的比较.(a) 式(47)与WCTSE, (b) 式(48)与WCTSE (吴学仁等2019)

图22圆盘中心和边缘裂纹的三种II 型格林函数结果比较. (a) 中心裂纹, (b) 边缘裂纹 (Xu et al.2020a)

用规范化解析权函数法求得的II 型裂纹和各向异性材料裂纹的格林函数也有很好的精度.图22 给出了用4 种方法(Wu-Carlsson 规范化解析权函数法、Fett 的边界元法及DAM 权函数法、有限元法)得到的圆盘II 型中心和边缘裂纹的3 种格林函数比较. 对于圆盘中心裂纹: 规范化解析权函数法、有限元法和Fett 边界元法获得的II 型格林函数吻合非常好. 3 种方法的结果相对差别在0.8%以内. 对于圆盘边缘裂纹: 用规范化解析权函数法得到的II 型格林函数与有限元法的结果符合很好; 而DAM 法(Fett 1992, Fett & Munz 1997)的II 型格林函数与有限元结果则存在明显差别:α≥ 0.7 时, 局部超过10%.

图23(a)给出了规范化解析权函数法和有限元法计算得到的单边缺口正交各向异性板(ρ=6.395)的格林函数(I 型)结果的比较, 可见二者高度一致. 这为规范化解析权函数法用于各向异性材料的裂纹问题分析提供了支持; 图23(b)显示了材料各向异性对权函数/格林函数的影响,可见在短裂纹阶段(α＜ 0.3)影响较大(Xu et al. 2020b, 吴学仁等 2019, Wu & Xu 2020).

以上比较表明, 规范化解析权函数法对II 型和各向异性材料裂纹问题分析同样也有高精度.

图23正交各向异性(ρ = 6.395)有限板单边裂纹的格林函数以及与各向同性板的比较. (a) 规范化解析权函数法和有限元法获得的格林函数比较, (b) 各向异性与各向同性有限板单边裂纹格林函数比较

3.3 解析权函数法的鲁棒性分析

本节从3 方面考察以上3 种解析权函数法的鲁棒性(robustness: a process or system able to withstand or overcome adverse conditions).

3.3.1 对参考载荷及其组合的敏感性

对参考载荷σr(ξ)的敏感程度从一个方面反映了权函数方法的鲁棒性. 为考察基于裂纹面张开位移的规范化权函数法对参考载荷的敏感性, 考虑裂纹面均布和非均布应力两种参考载荷, 采用裂纹嘴位移Vr(α)条件, 分别推导出两种裂纹几何的权函数并比较二者的差别.

(1) 有限宽板边缘裂纹. 分别以均匀拉伸(σr(ξ)/σ0= 1)和纯弯曲(σr(ξ)/σ0= 1 - 2ξ)作为参考载荷情况. 把推导得到的两个权函数m(α,ξ/α)转化为格林函数G(α,ξ/α)进行比较, 结果示于图24(a). 二者差别小于2% (Wu 1991b).

(2) 有限宽板圆孔边等长双裂纹.

取孔边的韧带宽度W=B-R为特征尺寸. 分别以远方均匀拉伸(裂纹面非均布应力)和裂纹面均布应力(σr(ξ) = 1)作为参考载荷推导权函数, 进而转化为格林函数G(α,ξ/α)作比较.图24(b)表明, 二者差别为-0.6% ～ 1.0%.

MRS 权函数法至少需要两种参考载荷. 由于不同的参考载荷组合会得到不同的权函数, 所以应考虑第二种参考载荷的选择及其对MRS 权函数的影响. 考虑有限宽板单边缘裂纹的两种不同参考载荷组合: 均布应力+弯曲应力; 均布应力+裂纹嘴集中力. 图25 是这两种不同参考载荷组合所得到的MRS 格林函数的差别, 可见基于参考载荷的不同组合得到的同一裂纹几何的MRS 权函数之间存在着不同程度差异. 其一般规律是中心裂纹差异较小, 边缘裂纹差异较大;Glinka-Shen 的通用权函数比Fett-Munz 的DAM 权函数的差异更加显著.

图24基于裂纹张开位移的规范化解析权函数对参考载荷的敏感性: 格林函数的差别(Wu 1991b, 吴学仁等 2019). (a) 有限宽板边缘裂纹拉伸与弯曲, (b) 有限宽板孔边双裂纹受远方拉伸和裂纹面均布应力

图25有限宽板单边缘裂纹在两种不同参考载荷组合下的MRS 格林函数差异. (a) Glinka-Shen, (b) Fett-Munz

无限板孔边单裂纹是一个更能揭示不同参考载荷组合和参考解的精度对Glinka-Shen 通用权函数影响的例子. Jin 等 (2017)采用两种远方拉伸(双轴应力比分别为1 和0)作为参考载荷,并用Tada 等 (2000)手册的K公式作为参考解, 结合几何条件mJ(x= 0) = 0, 推导权函数. 如果把其中的一个参考载荷(双轴拉伸应力比为1)改为圆孔内壁受均匀内压, 其余保持不变, 就得到另一个权函数. 图26 是这两个通用权函数(转化为格林函数后)的比值. 可见二者差别非常大,尤其是当无量纲裂纹长度很小时(图26(b),α= 0.01). 这表明Glinka-Shen 通用权函数法的精度对参考载荷的选择很敏感.

3.3.2 对参考解精度的敏感性

图26无限板孔边单裂纹不同参考载荷组合下的两种Glinka-Shen 通用权函数的比值. (a) α = 0.1 ～2.0, (b) α = 0.01

基于裂纹面张开位移的权函数法只需要一种参考载荷, 而MRS 权函数法需要至少两种参考载荷情况. 二者通常都把裂纹面均匀应力作为首选. 考虑有限宽板单边缘裂纹几何受远方拉伸,相关的无量纲K值(Ft)在文献中有两个解, 见图27(a). 它们的相对差别仅为-0.13% ～ 0.4%.MRS 权函数法需要的第2 种参考载荷(弯曲)K解(Fb)则保持不变; 几何条件均采用mJJ = 0.

为考察Ft微小变化对这两种MRS 权函数的影响,分别基于两个差别很小的Ft推导出两个权函数. 结果表明, Wu-Carlsson 权函数(格林函数)相当稳定, 最大差别小于±1.0%, 见图27(b).而Fett-Munz 的DAM 权函数和Glinka-Shen 通用权函数则差别显著, 尤其是当裂纹很短时, 最大差别分别达到约24%和20%, 分别见图27(c)(d). 这说明Wu-Carlsson 权函数法对Ft的微小变化不敏感, 而两种MRS 权函数法则相当敏感. 这其实是MRS 权函数方法本身固有的问题, 与第一类伏尔特拉积分方程固有的病态/不适定性有关, 见3.4 节.

3.3.3 对裂纹嘴几何条件的敏感性

Glinka-Shen 通用权函数法对边缘裂纹的裂纹嘴几何条件有两种选择: (1)mJJ = 0; (2)mJ =0. 为避免出现通用权函数的系数M2= 3 的问题, Glinka 和 Shen (1991)在有些情况下改用mJ =0. 这个条件对于提高半无限板边缘裂纹权函数的精度是有利的. 但对于有限板单边缘裂纹却是有害的, 其影响随裂纹长度增大变得更加严重. 这是因为mJ = 0 条件强令裂纹嘴处格林函数曲线的斜率为零, 迫使曲线发生畸变.

以有限宽板单边缘裂纹为例. 基于两个参考载荷情况的两种组合: (a) 拉伸 + 弯曲; (b) 拉伸+ 裂纹嘴集中力, 采用几何条件mJ = 0 得到的两种格林函数见图28. 与正确的格林函数(图12(b))相比, 这两种Glinka-Shen 通用权函数的格林函数曲线发生了严重畸变, 甚至出现违背物理意义的负值. 这表明Glinka-Shen 通用权函数对几何条件的高度敏感性. 然而图28(a)和(b)中的格林函数(权函数)不但都能够准确复现两种参考载荷条件下的K值, 而且对于与参考载荷相近的新载荷情况, 用这些权函数得到的K值精度则与参考解的精度很接近. 这就容易造成这些有问题的权函数却精度很好的假象. 而当载荷情况明显有别于所用的两种参考载荷时, 用这样的权函数计算的K结果就出现很严重的精度问题(Hill & Kim 2016).

图27三种权函数法对有限宽板单边缘裂纹参考解精度的敏感性比较(吴学仁等2019). (a) 远方拉伸的两个无量纲应力强度因子曲线, (b) Wu-Carlsson, (c) Fett-Munz, (d) Glinka-Shen

3.4 对MRS 权函数反向求解的讨论

Glinka-Shen 的通用权函数法UWFM 和Fett-Munz 的直接调整法DAM 尽管在一些细节上有区别, 但总体思路是相同的: 二者都是先假设权函数的某种级数表达形式, 然后基于多种(一般为2 种)参考载荷σri(ξ)和相应的应力强度因子Kri(a), 并结合裂纹嘴处的一个几何条件, 通过求解联立方程组得到所假设的权函数级数表达式中的2 ～ 3 个系数进而确定权函数. 从数学视角看, 这种方法是以σri(ξ)和相应的Kri(a)作为已知条件, 通过以下方程反(逆)向求解被积函数中的权函数m(α,ξ/α).

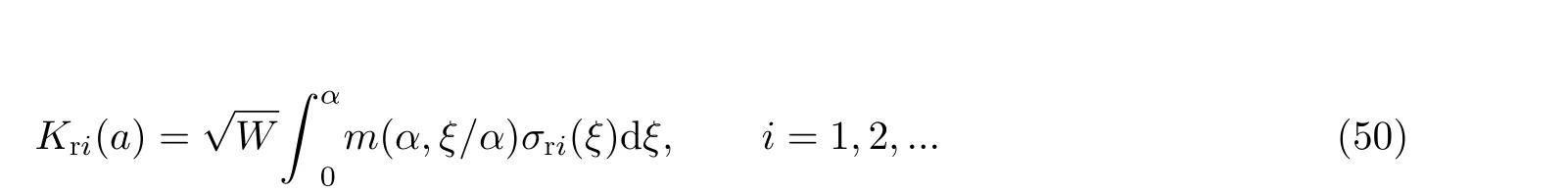
式中的权函数m(α,ξ/α)表达式分别见式(34), (37)和(38).

式(50)是第一类伏尔特拉积分方程(volterra integral equation of the first kind)在裂纹问题中的具体表达(Schajer & Prime 2006, Babolian & Masouri 2008). 这是数学上的一个反问题(inverse problem).

图28由Glinka-Shen 通用权函数法得到的有限板单边缘裂纹格林函数(采用几何条件mJ = 0). 参考载荷: (a) 拉伸+弯曲, (b) 拉伸+集中力 (吴学仁等2019)

式中k(t,s)为核函数(kernel function), 它对应于式(50)中的权函数m(α,ξ/α). 函数f(t)和x(s)则分别对应于K(a)和σ(ξ). 通常情况下是由已知核函数k(t,s)和f(t)反向求解未知函数x(s).5.5 节中讨论的问题与之类似, 即由已知权函数m(α,ξ/α)和应力强度因子K(a), 反向求解裂纹面应力分布σ(ξ). 而这里则是要从已知σ(ξ)和K(a)反向求解核函数k(t,s), 即权函数m(α,ξ/α). 由于m(α,ξ/α)不但有奇异性, 而且还有两个变量, 其反向求解的难度和不确定性比求解单变量的应力分布σ(ξ)要大得多. Glinka-Shen 和Fett-Munz 的解法是通过预设m(α,ξ/α)的某种级数表达形式, 再利用已知两种参考载荷σri(ξ)及其应力强度因子Kri(a), 以及裂纹嘴处的一个几何条件, 把m(α,ξ/α)的推导转化为通过联立方程组求解m(α,ξ/α)表达式中的2 ～ 3 个系数(Mi或Dn)的问题. 从数学的视角看, 第一类伏尔特拉积分方程的反向求解有较大难度和不确定性.Schajer 和Prime (2006)指出: 反方程(inverse equations)对“数据噪声(data noise)”很敏感, 很少能够得到如正方程(forward equations)那样明晰确定的解, 所以对反问题的求解不能有很高期望; 在某种意义上, 反方程的“解”只能被认为是一个“最佳猜想(best guess)”; 高质量的原始数据是求解反方程的关键要求. Babolian 和Masouri (2008)指出: 第一类伏尔特拉积分方程是一个固有的病态/不适定问题(inherently ill-posed problem), 这意味着方程的解通常是不稳定的, 所求解的问题即使有小的变化就会引起解的很大变化, 小误差会导致解的无界误差(unbounded error).

这里以圆盘单边缘裂纹为例, 说明反向求解得到的MRS 权函数不具备唯一性. 采用裂纹面两种参考载荷情况: (1)均布应力σ(x)/σ0= 1; (2)抛物线分布应力σ(x)/σ0= (1 - 2x)2. 这两种载荷作用下的应力强度因子都有精确解(Gregory 1977, 1979), 均属于高质量的原始数据. 推导中采用的几何条件mJJ(x= 0) = 0 也相同. 根据这些信息, 可以分别推导出两种MRS 权函数. 图29是求得的圆盘单边缘裂纹的Glinka-Shen 的通用权函数和Fett-Munz 的DAM 权函数(转化为格林函数后)的比值, 二者差别显著, 最大达-8% ～ 15%. 由于推导所用的基础数据完全相同, 因此可以肯定: 导致这些差别的唯一原因是两种权函数的级数基本项的幂指数不同: Glinka-Shen 为(1 -x/a)n/2, 而Fett-Munz 为(1 -x/a)n+1/2. 这个细节区别使得两种MRS 权函数产生明显差异.这也表明了第一类伏尔特拉积分方程反向求解结果的不确定性.

图29采用相同的两个精确参考解和几何条件, 反向解得的圆盘单边缘裂纹两种MRS 权函数的比值(吴学仁等2019)

以上是文献中从数学角度对第一类伏尔特拉积分方程求解的难度和不确定性的一些评论.它们对于理解基于多个参考载荷条件的MRS 权函数法存在的各种问题, 提供了有益启示, 如:

(1) 基于相同的参考载荷和几何条件, 仅在级数基本项幂指数上的细微差别(1/2, 1, 3/2 与1, 2, 3)就能导致Glinka-Shen 和Fett-Munz 的MRS 权函数的明显不同.

(2) 采用同一种权函数方法, 参考载荷的选择和组合对MRS 权函数结果影响显著.

(3) 几何条件的选择对Fett-Munz 权函数影响相对较小, 但对Glinka-Shen 权函数影响十分显著, 主要原因是Glinka-Shen 权函数的基本项幂指数不符合弹性力学理论.

(4) 裂纹长度较小时, MRS 权函数的精度明显下降.

(5) 参考解精度的细微变化能导致MRS 权函数的很大变化.

3.5 小结

本节以高精度复变函数泰勒级数展开权函数WCTSE 为基准, 对采用不同方法得到的几种解析权函数进行了严格的验证评价. 结果表明, 基于一种参考载荷的裂纹面位移的规范化解析权函数法(Wu-Carlsson)在精度、稳定性和鲁棒性方面均优于基于多个参考载荷的两种MRS 权函数法(Fett-Munz 和Glinka-Shen). 这主要是因为, 基于裂纹面位移的规范化解析权函数法是以物理量COD 为基础推导确定权函数. 而基于多个参考载荷的两种MRS 权函数法则是建立在对多个参考载荷情况的纯数学拟合的基础上, 通过反向求解第一类伏尔特拉积分方程得到预设权函数表达式中的系数. MRS 权函数法对多种因素的高度敏感性和不稳定性等问题的根本原因 是脱离了裂纹问题的物理本质. 关于MRS 权函数法存在的上述几个主要问题及其原因, 笔者与Glinka 教授最近进行了深入讨论, 并达成一致认识(Glinka 2020).

对于有些很特殊的裂纹几何(如很纤细的双悬臂梁和裂纹附近有局部开孔等), 即使以裂纹面均布应力作为参考载荷, 其裂纹面位移也难以用规范化级数准确表达. 故Wu-Carlsson 解析权函数法对这类裂纹几何或难以适用. MRS 权函数法则因与COD 无关, 故应用不受影响.

图30 是综合多个评价维度, 用雷达图的形式对以上3 种应用广泛的解析权函数法的比较.采用的8 个维度是: (1) 理论的严密性; (2) 方法的规范性; (3) 权函数级数表达式的合理性; (4) 几何条件的统一性; (5) 推导快捷性和使用方便性; (6) 方法的鲁棒性; (7) 权函数的准确性(精度水平); (8) 精度验证的充分性. 其中以权函数的准确性/精度最为重要.

对两种MRS 权函数的综合比较表明, Fett (1992)与Fett 和 Munz (1997)的DAM 权函数法的精度优于Glinka 和 Shen (1991)的通用权函数法UWFM. DAM 权函数的级数表达是合理的,如果采用两个差别较大的参考载荷情况(如裂纹面均布应力和裂纹嘴集中力), 所得权函数的精度通常可以满足工程应用要求. I 型和II 型的DAM 权函数推导方法相同(Fett 2001, 2002). 这两种MRS 权函数在文献中都有广泛应用. 如文献(Fett et al. 1996, 2000)给出的功能梯度材料和涂层/基体材料有限板边缘裂纹几何的DAM 权函数, 被研究者们用于涂层裂纹的热冲击应力强度因子求解(Chen & You 2014, 彭中伏和陈学军 2018). Dong 等 (2004)利用DAM 的权函数求解了圆盘中心裂纹在集中力作用下的应力强度因子. Glinka 和 Shen (1991)的UWF 权函数在学术界应用也很广泛, 工业领域的应用如美国石油协会API 579 (2000), 美国空军AFGROW 软件(Harter 2008), 以及航空发动机部件损伤容限分析设计软件DARWIN (2008)等; 最近还被用于功能梯度材料圆筒多裂纹的权函数分析和应力强度因子求解(Nabavi & Rekavandi 2020). 应用这两种MRS 权函数求解K时应注意: 当所考虑的载荷和两种参考载荷引起的无裂纹应力分布比较接近时, 求得K值的精度会与两种参考解K本身的精度相当; 而对于明显偏离的无裂纹应力分布, 所求得K值的精度则可能出现问题.

二维裂纹问题的规范化解析权函数法(Wu & Carlsson 1991)在近30 年中得到了国际断裂界同行学者的广泛验证, 并用于分析各种类型的裂纹问题, 其中的一些代表性论著见(Cardona et al. 1993; Wang & Kemeny 1993; Lorenzo et al. 1994; John et al. 1995; Dempsey & Adamson 1995; Lee & Hong 1995; Adamson et al. 1996; Fleck et al. 1996; Bazant & Planas1997; Jones 1998; Ng & Lau 1999; Zhuang 2000; Ostlund & Karenlamp 2001; Wu & Bowen 2000; Chen & Sun 2001; Lim et al. 2003; Zerbst et al. 2003, 2005, 2007; Ball & Watton 2011; Ball 2008; Ball et al.2014; Wagner & Millwater 2012; Dempsey & Mu 2014; Ribeiro & Hill 2016); 此外, 还被多个国外工业规范如R6 (2009), BS 7910 (Zerbst et al. 2007, Andersson et al 1999, Dillstrom et al. 2018)以及大型软件如NASCRAC (1994), NASGRO (2012), DARWIN (2008)采用. 在国内, 由该方法得到的各种裂纹几何的权函数和大量应力强度因子解被编入中国航空研究院(1993)应力强度因子手册和军用飞机疲劳-损伤容限-耐久性设计手册(1994). Wu-Carlsson 权函数法也得到了国内断裂力学界多位学者的关注 (杨卫 1995, 匡振邦和马法尚 2002, 庄茁和蒋持平 2004, 王自强和陈少华 2009), 北京航空航天大学主编的研究生教材对该方法作了具体介绍(郦正能等 2012).

图30三种解析权函数方法综合比较的雷达图(吴学仁等 2019)

关于Wu-Carlsson 规范化解析权函数法以及二维裂纹解析权函数m(α,ξ/α)推导和验证和以此求得的大量应力强度因子解及其各种工程应用, 可参阅作者及其合作者的专著 (Wu & Carlsson 1991, 吴学仁等 2019, Wu & Xu 2022), 以及相关文章(Wu & Carlsson 1983; Wu 1984, 1991a,1992, 2019; 吴学仁和黄新跃 1988; 童第华等 2017; 赵晓辰等 2018; Wu & Tong 2018; Wu et al.2018a; Xu & Wu 2012; Xu et al. 2014, 2020a, 2020b).

4 三维裂纹问题的权函数法

三维裂纹(部分穿透裂纹)包括内埋裂纹、表面裂纹和角裂纹三种几何形态, 通常以椭圆或部分(半/四分之一)椭圆表示. 由于三维裂纹几何包含椭圆长/短轴两个尺寸, 且应力强度因子沿裂纹前缘位置(参量角φ)变化, 其权函数推导比二维裂纹问题复杂得多. 早期的三维裂纹权函数法仅考虑椭圆长/短轴两个端点(φ= 0, π/2)的应力强度因子的近似求解. Cruse 和Besuner(1975)提一种了用于计算三维裂纹两个端点的均方根(RMS)应力强度因子的方法. Shen 和Glinka (1991)的三维权函数法则给出椭圆长短轴两个端点的K值. Mattheck 等 (1983) 与 Xu和Wu (1989)采用Petroski 和Achenbach (1978)的二维裂纹位移表达式推导表面裂纹的近似权函数, 计算了最深点及表面点处的局部平均应力强度因子. Wang 和Lambert (1995, 1997)利用三维有限元法得到的应力强度因子参考解, 采用二维裂纹权函数形式推导表面裂纹和角裂纹的权函数, 但只能处理单方向的应力变化情况.

由Fujimoto (1976)首次提出的片条合成法克服了构造三维位移场导致的局限性, 能给出三维裂纹前缘各点的应力强度因子. 但其片条合成模型把片条完全作为二维裂纹问题处理, 不考虑未开裂部分对含裂纹片条的约束作用, 故误差较大. Dill 和Saff (1978), Saff 和Sanger (1984)用片条合成法分析了有限板表面裂纹和孔边角裂纹问题, 虽然考虑了板的刚度对片条的约束, 但未把这种约束作为普遍的性质纳入分析模型.

赵伟(1988)和Zhao 等 (1989a, 1989b)提出了三维裂纹的片条合成权函数法(Zhao-Wu-Yan). 这种方法将Fujimoto 片条合成技术与二维权函数法相结合, 对三维裂纹几何作离散化处理并转化为两组正交的二维片条模型, 利用其极限情况对应的二维权函数构造出片条的权函数.借助内埋椭圆裂纹的解析解, 考虑了未开裂部分对含裂纹片条的约束作用. 由两组正交片条的二维权函数求得的K解合成得到三维裂纹前缘各点的K(φ)值. 该方法不但求解效率明显高于有限元法, 而且精度可靠, 被广泛用于多种三维裂纹几何在各种载荷下的应力强度因子计算和建模分析 (赵伟等1990, 1991a, 1991b, 1991c; Zhao et al. 1997a; 吴学仁等 2000).

求解三维裂纹问题的另一类重要方法是点载荷权函数法. 这类方法能够计算在椭圆长短轴两个方向同时变化的双变应力场(bi-variant stressing)作用下的三维裂纹应力强度因子, 对于复杂双变应力场中的三维裂纹的损伤容限分析有重要价值. Gao 和Rice (1987)利用无限大体内埋圆形裂纹在一对集中力作用下的应力强度因子解, 用摄动法求解了无限大体含近似圆形裂纹的应力强度因子及裂纹面位移. Rice (1989)提出了一种通用的内埋三维裂纹权函数形式. Wang 和Glinka (2009)采用Rice (1989)的研究结果提出了由应力强度因子参考解推导内埋裂纹点载荷权函数的方法. Jin 和Wang (2013)在此基础上给出了表面裂纹的点载荷权函数. Orynyak 和Borodii (1994)采用椭圆坐标系建立分析模型, 提出了另一种形式的点载荷权函数, 无需应力强度因子参考解即可计算无限大体内埋裂纹的应力强度因子. Orynyak 等 (1994)通过对无限大体内埋裂纹权函数的修正, 提出了由参考解推导有限体三维裂纹点载荷权函数的方法. McClung等 (2004, 2013)和Lee 等 (2008)针对双变应力作用下的应力强度因子计算需求, 在Orynyak 和Borodii (1994)方法的基础上, 考虑有限体的边界修正, 提出了一种新的点载荷权函数法, 并对此作了广泛验证(Sobotka & McClung 2019). 赵晓辰(2016)通过改进 Orynyak 点载荷权函数法, 提高了宽范围椭圆长短轴比值的三维裂纹K求解精度.

本节简单介绍片条合成权函数法和几种不同形式的点载荷权函数法.

4.1 片条合成三维权函数法

赵伟 (1988), Zhao 等 (1989a, 1989b), 以及赵伟等(1990)结合二维裂纹解析权函数法和改进后的Fujimoto (1976)片条合成技术, 考虑未开裂部分对含裂纹片条的约束作用, 建立了求解三维应力强度因子的片条合成权函数法(slice synthesis weight function method, SSWFM). 这种方法的基本思想是把三维裂纹几何转化为等效的二维片条模型. 借助于无限体内埋椭圆裂纹的解析解模拟三维裂纹的所有特征. 通过把三维裂纹体离散化为两组含穿透裂纹的二维片条, 将未开裂部分对片条的约束作用转化为片条在裂纹扩展前方边界上的弹性位移边界条件, 并利用两种极限情况下对应的二维裂纹权函数, 构造出具有三维性质的片条权函数. 采用二维权函数法计算两组片条的应力强度因子, 进而根据所推导出的三维裂纹应力强度因子与二维裂纹片条应力强度因子的关系, 最终确定三维裂纹前缘各点的K(φ)值. 该方法已成功用于各类三维裂纹几何在多种复杂应力条件下的应力强度因子计算, 其求解精度已得到广泛验证.

4.1.1 基本理论与模型

三维裂纹片条合成权函数法SSWFM 的基本理论与分析模型可用图31 的孔边双角裂纹(1/4 椭圆)为例阐明. 将裂纹体的开裂部分沿椭圆长/短轴线分割为两组正交且厚度为无限小的片条, 与a轴平行的称为a片条, 与c轴平行的称为c片条. 选其中的一组作为基本片条, 其弹性模量及承受的外载荷均与三维裂纹体相同. 由于相邻片条之间的互相作用, 片条中存在着垂直于裂纹面方向的剪应力. 其作用可通过在裂纹面上施加弹簧力S(x,y)加以模拟. 另一组片条称为弹簧片条, 它仅在裂纹面上承受与基本片条的弹簧力大小相等方向相反的弹簧力, 但不承受外载荷. 通过施加在片条裂纹扩展前方边界上的弹性位移约束, 模拟三维裂纹体未开裂部分对片条的约束作用.a片条与c片条边界上的弹性位移约束刚度ki(i=a,c)与约束面积Ri(i=a,c)正相关. 当Ri= 0 时,ki= 0 时, 片条边界上没有约束; 当Ri→∞时,ki→∞时, 片条边界承受完全限制法向位移的固定约束. 由两个极限状况的二维权函数可构造得到片条权函数.

考虑无限板情况, 即(c+r)/b→0, 此时片条约束为Ri→∞,Ti(∞) = 0, 孔边对称双角裂纹的二维片条权函数为

其中mdouble为有限板双边裂纹权函数,mhole-edge-double为无限板孔边双裂纹权函数. 确定片条二维权函数mi(i=a,c)后, 由下式计算两组片条的二维应力强度因子Ki(i=a,c)

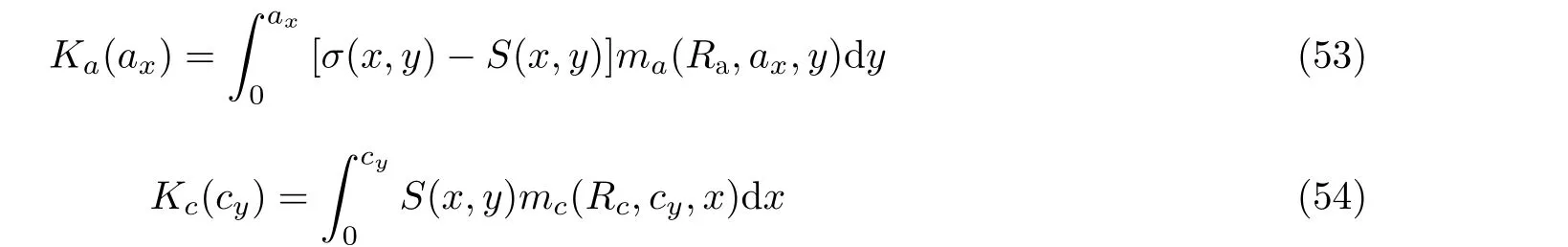
式中σ(x,y)为外载荷作用下假想裂纹处的应力分布;S(x,y)为弹簧力, 其表达式设为

根据两组片条在对应于裂纹面相同位置处的位移相等的协调条件, 通过求解位移协调方程可确定弹簧力S(x,y). 求解所需的片条裂纹面位移Va和Vc则通过二维裂纹权函数法求得

令两组片条所对应相同位置处的裂纹面张开位移相等, 则可建立确定弹簧力S(x,y)的方程

采用全主元高斯-约当消元法求解, 即可确定式(57)中的弹簧力S(x,y)的系数αi. 代入式(53)和(54)便得到二维片条的应力强度因子Ki(i=a,c), 进而按下式计算三维裂纹前缘各点的K(φ)值

图31有限板圆孔边四分之一椭圆角裂纹的片条分析模型. (a) 三维裂纹体, (b) 片条裂纹长度及椭圆参量角, (c) 基本片条(a 片条), (d) 弹簧片条(c 片条).

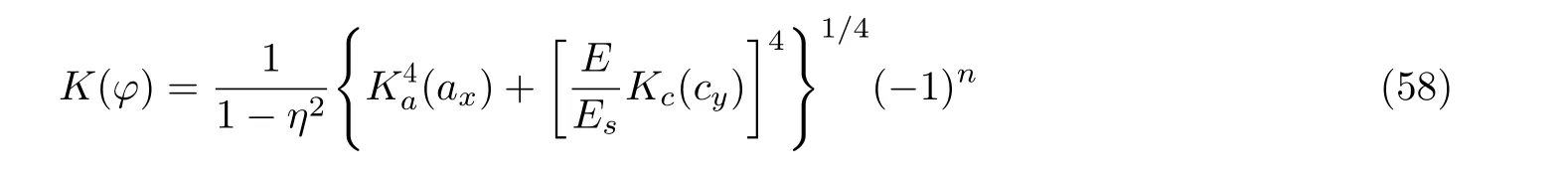
式中参量角φ表征裂纹前缘位置, 其定义见图31(b). 若φ所示位置在裂纹体内部, 则η=ν; 若在自由表面, 则η= 0. 若Ki＜ 0 (i=a,c),n= 1; 若Ki≥ 0,n= 2. 有关细节可参阅: 赵伟(1988),Zhao 等 (1989a, 1989b, 1997a), 赵伟等(1991a, 1991b, 1991c), 以及吴学仁等(2000).

位于厚度较大的结构部位的三维裂纹可能受沿长/短轴两个方向变化的应力(双变应力: bivariant stress)作用. 这种情况要用能处理复杂双变应力的三维权函数法. SSWFM 在理论上具有处理双变应力的三维裂纹问题的能力. 对于图32(a)的厚板圆孔根部的三维裂纹, 其裂纹面应力在板的宽度和厚度两个方向变化. 这类双向变化应力场可用下式表示(Zhao et al. 1994)

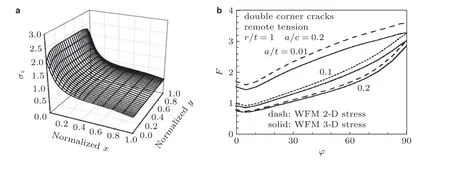
图32(a) 无限板圆孔边沿x 和y 两个方向变化的三维应力场, (b) 用SSWFM 结合二维和三维有限元分析的应力场得到的孔边角裂纹无量纲应力强度因子. 实线: 用2D 应力解, 虚线: 用3D 应力解(Zhao et al. 1997b)

图32(b)的SSWFM 计算结果表明, 采用二维和三维有限元计算得到的裂纹面应力分布通过三维权函数法得到的K(φ)值会有差别. 表面裂纹差别较小, 角裂纹则较为显著(Zhao et al.1997b, 1998). 差别的程度随裂纹相对尺寸(a/t)变化, 并与孔半径与板厚的比值(r/t)有关,r/t越小则变化越大. 弹性力学对平面问题的应力分析不考虑应力沿板厚方向(t)的变化, 给出的裂纹面应力σ(x)与真实的σ(x,y)会有差别, 导致所得应力强度因子误差. 所以对于应力集中部位的三维裂纹K权函数法求解, 宜采用三维有限元的σ(x,y)分析结果.

与其他三维裂纹权函数法相比, SSWFM 有诸多优势, 如: 权函数的确定不需要大量三维数值计算, 而是通过已知的二维片条的解析权函数结果(Wu 1984, Wu & Carlsson 1991)合成得到;在许多情况下不需要三维裂纹的参考解; 所得到的K值具有高精度. 这种方法已成功用于多种三维裂纹问题的分析计算, 如: 小表面裂纹和角裂纹(赵伟等 1991b, 1991c), 圆孔边和半圆缺口根部表面裂纹和角裂纹(Zhao et al. 1990a, 1990b, 1991,1997a, 1998; Zhao et al. 2016, 2017). 需要注意的是, SSWFM 对于处理带有(x/c)n(y/a)m交叉项的裂纹面应力分布的能力尚待广泛验证.但这类特殊应力场在三维裂纹问题中不常见, 特别是对于裂纹尺寸较小的情况. 近期用SSWFM 计算得到了多种三维裂纹几何在裂纹面幂函数应力 (σ(x, y)/σ0= (x/c)n,σ(x, y)/σ0= (y/a)n,n= 0 ～ 4)作用下的大量应力强度因子Fn(吴学仁等 2019). 这些Fn值与叠加原理结合, 只需通过简单四则运算就能方便地求得在裂纹面多项式应力作用下三维裂纹前缘各点的应力强度因子. 计算效率比有限元等数值方法一般能高出2 ～ 4 个数量级.

文献检索表明, 赵伟及其合作者建立的三维裂纹SSWFM 已被国内外研究者用来分析各种类型的三维裂纹问题. 典型例子如: 表面裂纹的条带屈服分析(Daniewicz 1998, Daniewicz &Aveline 2000, Kim & Lee 2000), 齿轮根部的三维裂纹应力强度因子计算(Guagliano & Vergani 2001), 残余应力场中的表面裂纹分析(汤英等 2012), 单边缺口弯曲SENB 试样的表面裂纹和角裂纹(Zhao et al. 2016, 2017)以及孔边两条不对称角裂纹在多种载荷下的应力强度因子计算(Zhang et al. 2022). 所得到的结果都具有良好的精度. 基于SSWFM 求得的单边缺口拉伸SENT试样的两种三维裂纹应力强度因子的拟合公式被我国航空工业标准采用（HB7705-2001）.

4.1.2 典型三维裂纹应力强度因子SSWFM 求解精度验证

由于尚无三维裂纹几何的格林函数(与作用在裂纹面任意点的单位集中力P对应的裂纹前缘各点的K(φ)值), 对二维裂纹权函数的基于格林函数的评价方法难以用于三维裂纹情况. 所以只能基于一些载荷情况下的K(φ)值对三维权函数的精度作评价比较.

SSWFM 求得的多种三维裂纹在复杂载荷情况下的应力强度因子结果已经与有限元结果作了广泛比较, 二者普遍符合得很好. 除了受边界层效应影响的自由表面区域外, 与有限元结果的差异一般不超过3%, 最大差别在5%以内. 图33(a)是孔边表面裂纹应力强度因子结果的对比(Newman et al. 1994). 值得指出的是, 基于SSWFM 的计算结果, 曾发现了早期NASA 有限元模型中因近表面区域内的病态单元(ill-shaped elements)引起K急剧下降的问题. 纠正病态单元后的有限元结果与SSWFM 和其他数值解法的结果符合很好(Tan et al. 1988, 1990, Newman et al.1994). 图33(b)是Bakuckas (2001)对用各种数值方法(有限元法, 边界元法等)和SSWFM 的孔边角裂纹在远方拉伸载荷下的无量纲应力强度因子F的比较, 这些方法间的差异均在±3%的分散带内. 图34 是中美CAE-NASA 合作项目的结果: 用SSWFM 和有限元法得到的SENT 试样半圆缺口根部表面裂纹及角裂纹的应力强度因子符合得很好(Newman et al. 1994, Wu et al.1998).

图33(a) 孔边表面裂纹远方拉伸下的应力强度因子: SSWFM 结果与有限元解的比较(Newman et al.1994, Wu et al. 1998), (b) 孔边对称双角裂纹远方拉伸下的应力强度因子: SSWFM 与各种数值解法的比较(Bakuckas 2001)

2021 年, 笔者团队参加了由美国断裂力学界发起的一个孔边角裂纹三维应力强度因子计算方法的Round Robin 双盲比对活动(Newman & Wu 2021). 图35 是各参加单位用不同方法得到的计算结果汇总比较. 其中, FEA(p版有限元)所用自由度高达160 000, 建模和计算工作量很大.SSWFM 给出的两种结果(WFM3D)是分别基于2D 和3D 有限元应力分析得到的, 即σ(x)和σ(x,y). 二者之间存在少许差别, 但都在合理分散带范围内. 基于3D 有限元应力σ(x,y)的结果与其他解的符合程度更好些. 这个比对为SSWFM 的高效高精度优势提供了最新佐证.

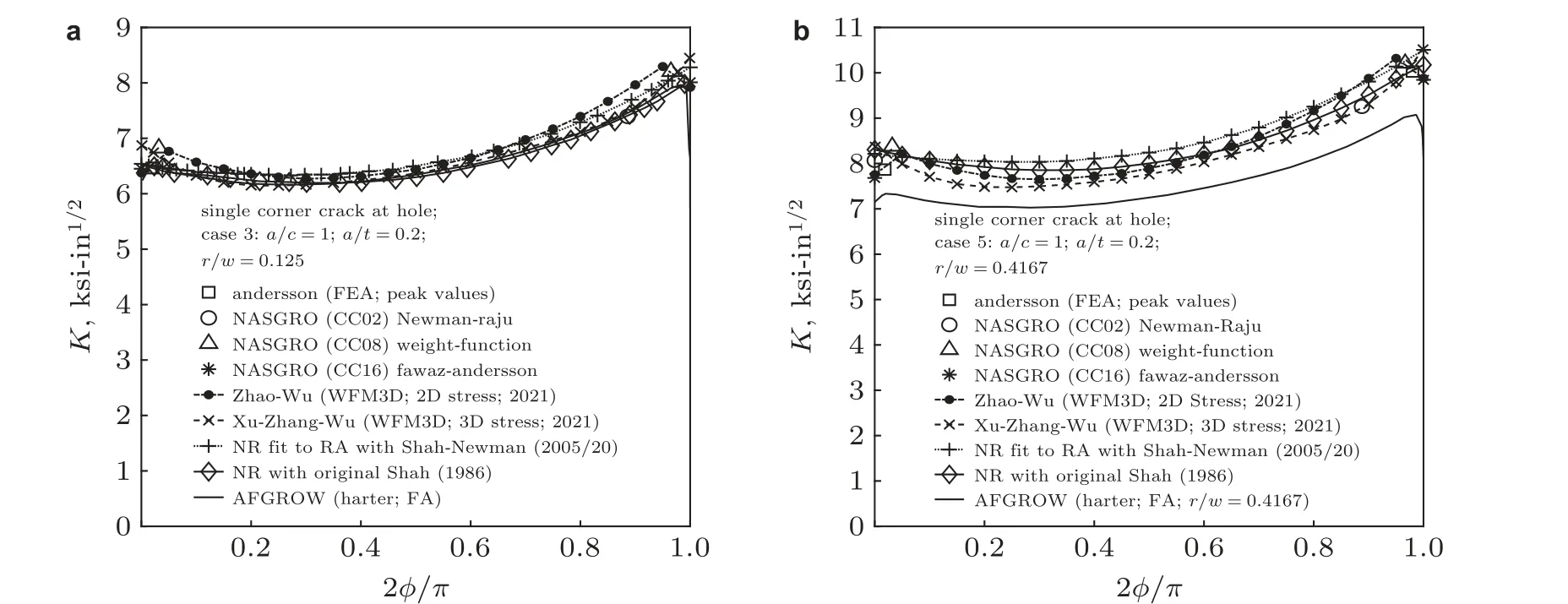
图35 9 种方法求得的远方拉伸无限板孔边角裂纹(r/t = 1.0, a/c = 1.0, a/t = 0.2)三维应力强度因子比较(ERSI-USA). (a) r/W = 0.125, (b) r/W = 0.416 7 (Newman & Wu 2021)

以上SSWFM 分析考虑的是圆孔单边角裂纹和双边对称角裂纹情况. 笔者团队最近进一步发展了适用范围更广的SSWFM. 通过合理考虑弹簧片条的两种极限边界约束条件, 有效提高了该方法在裂纹相对尺寸(a/t)较大时的求解精度. 图36 是解得的无限板圆孔非对称双角裂纹在远方拉伸和面外弯曲载荷下的无量纲应力强度因子f, 以及与Franc3D 有限元结果的比较, 二者符合得很好. 而SSWFM 计算速度则是Franc3D 的500 倍(Zhang et al. 2022).

4.2 点载荷权函数法

图34远方拉伸SENT 半圆缺口试样三维应力强度因子: SSWFM 与有限元结果以及拟合方程比较.(a) 表面裂纹, (b) 角裂纹 (Newman et al. 1994; Wu et al. 1998)

式中,S为整个裂纹面,x和y为裂纹面坐标,P′为位于裂纹前缘的点,σ(x,y) 为裂纹面应力,m(x,y;P′)为点载荷权函数. 本节主要讨论应用较多的3 种点载荷权函数法, 分别是Orynak-Borodii 点载荷权函数法, Wang-Glinka 点载荷权函数法和McClung-Lee 双变应力场点载荷权函数法. 无限体内埋裂纹点载荷权函数的确定相对简单. 有限体以及有自由表面的表面裂纹和角裂纹等三维裂纹几何, 则需利用其他方法求得的三维应力强度因子参考解, 反算求得修正系数后才能确定点载荷权函数.

4.2.1 Orynak-Borodii 点载荷权函数法

基于Guidera 和Lardner (1975)的无限大体内埋圆形裂纹的点载荷权函数精确解, Orynyak et al. (1994), 以及Orynyak 和Borodii (1995) 采用椭圆坐标系提出了无限大体内埋椭圆裂纹的点载荷权函数, 见图37.

图37 Orynyak-Borodii 点载荷权函数分析模型. (a) 内埋椭圆裂纹, (b) 半椭圆表面裂纹, (c) 四分之一椭圆角裂纹

图36无限板孔边两条非对称角裂纹(r/t = 1.0)在远方拉伸和面外弯曲载荷下的三维应力强度因子:SSWFM 与有限元软件Franc3D 结果的比较. 裂纹面应力分布σ(x, y)采用了3D 有限元分析结果(Zhang et al. 2022)

式中lPP’为点P(ξ,η)到点P’(ξ0,η0)之间的距离.ξ和η为P点的椭圆坐标,ξ0和η0为P′点的椭圆坐 标,ξ0={ln[(1+β)/(1-β)]}/2 , 若a/c＜ 1.0, 则β=a/c; 若a/c＞ 1.0, 则β=c/a.R为 点P1(ξ0,η)与P2(0,η)的距离;r为点P(ξ,η)和P2(0,η)的距离. 点P,P1与P2沿椭圆角η分布. 式(61)仅适用于椭圆半轴长度(a,c)不相等的情况.

为考虑有限尺寸对应力强度因子的影响, 在式(61)基础上增加修正项ν(ξ,η;P′) , 可把有限体内埋椭圆裂纹的点载荷权函数写为

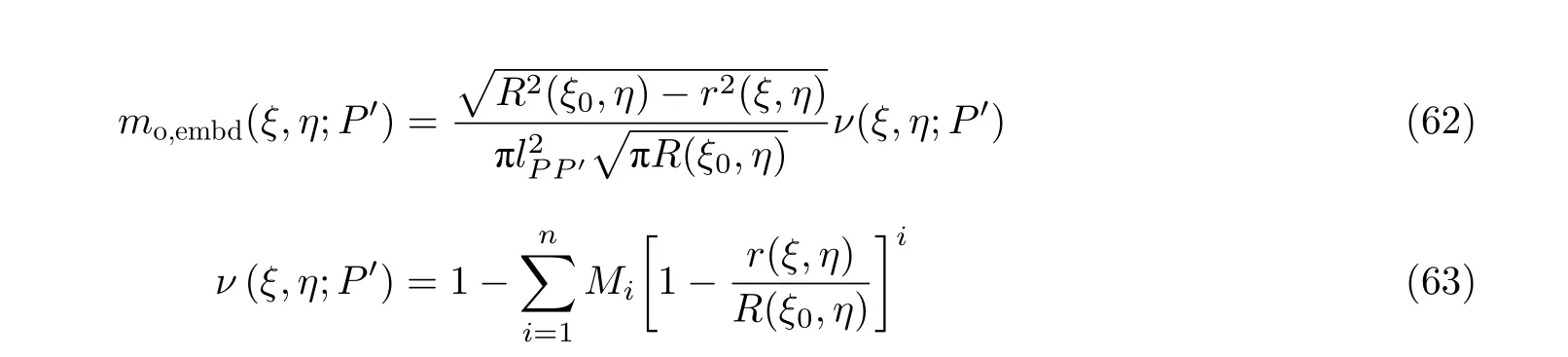
对于表面裂纹(图37(b))和角裂纹(图37(c)), 为考虑自由表面(表面裂纹1 个, 角裂纹2 个)的影响, 增加新的修正项. 相应的点载荷权函数表达式为

表面裂纹

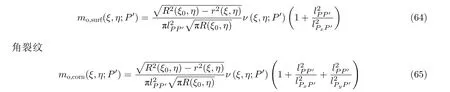
其中, 点Px与点P沿x轴对称,lpxp′是Px到P′的距离; 点Py与点P沿y轴对称,lpyp′是Py到P′的距离.

在修正多项式(63)中, 取n= 1, 则可利用一种参考载荷下的已知应力强度因子Kr, 由式(60)求得修正系数M1. 以有限体内埋裂纹为例, 将权函数式(62)及参考载荷代入式(60), 则有

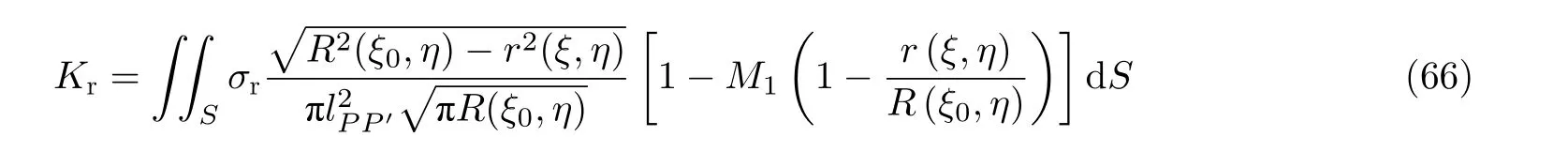
式中σr为参考应力,Kr为对应的应力强度因子参考解. 完成二重积分后, 通过简单的代数运算由Kr得到系数M1. 为简化求解一般以裂纹面均布载荷σ(x,y)/σ0= 1 作为参考应力. 但文献中关于参考应力的选择对系数M1的影响未见考虑.

赵晓辰(2016)利用Orynyak-Borodii 点载荷权函数法计算了多种载荷情况下的表面裂纹K值, 发现这种方法的求解精度与椭圆长短轴的比值(a/c)有关,a/c＜ 1 时精度较好,a/c＞ 1 时精度变差. 为拓宽该方法对a/c比值的适用范围, 提出增加1 项修正系数, 并采用更合理的幂指数(1/2, 3/2). 为此需要2 种参考载荷情况及其参考解, 以确定下式中的系数M1和M2

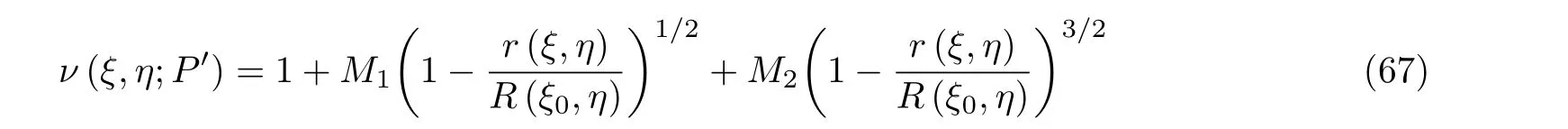
为提高计算效率, 利用片条合成权函数法计算单变载荷下的应力强度因子作为参考解. 通过片条合成权函数法与宽范围点载荷权函数法的结合, 确定各种有限体三维裂纹几何的点载荷权函数, 进而计算裂纹面在几种受单变和双变应力作用下的应力强度因子, 并对部分结果进行了比较验证. 结果表明, 新方法提高了a/c＞ 1 的求解精度, 拓宽了适用范围, 并明显减少了求解工作量(赵晓辰 2016). 但这种方法尚待进一步验证和改进.

4.2.2 Wang-Glinka 点载荷权函数法

Rice (1989)建立了内埋椭圆裂纹的权函数分析模型(图38), 并指出裂纹前缘点P′(x′,y′)的点载荷权函数都可以表示成单位载荷加载点P(x,y)到裂纹前缘的最短距离s, 以及P到P′距离lPP′的函数

式中点Px为与点P沿x轴对称的点,lpxp′为Px到P′的距离, 见图38(b).

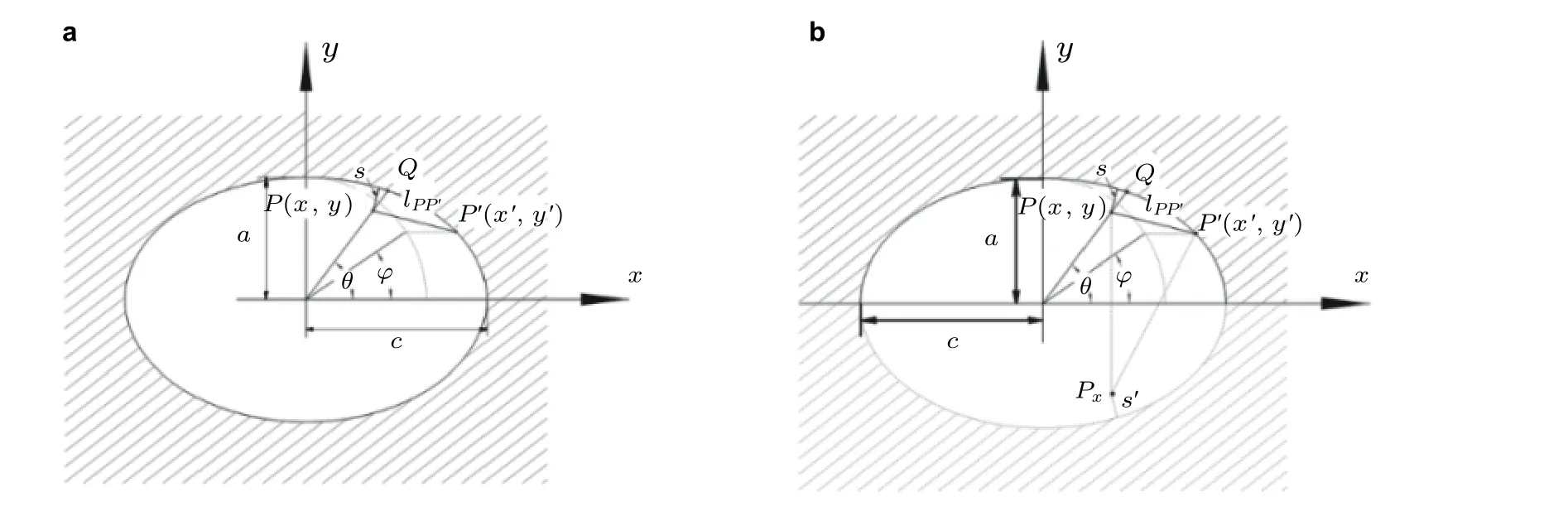
图38 Rice (1989)点载荷权函数分析模型. (a) 内埋椭圆裂纹, (b) 半椭圆表面裂纹

袁奎霖(2019)用Wang-Glinka 和Jin-Wang 点载荷权函数法计算了焊接结构的焊趾表面裂纹(a/c= 0.05 ～ 1)受σ(x,y)/σ0= (1 -y/a)mcos[(πx)/(4c)]双向变化应力作用的应力强度因子,结果与有限元解的差别在10%以内. 最近Guo 等 (2021)采用点载荷权函数法计算了圆孔边角裂纹在单/双向幂函数应力σ(x,y)/σ0= (x/r)n和σ(x,y)/σ0= [(xy)/(ac)]n, (n= 0 ～ 3)作用下的应力强度因子, 与文献中的解和有限元计算结果符合较好. 赵晓辰(2016)用该点载荷权函数法计算了表面裂纹几种载荷情况的K值. 与有限元解的比较表明, 其求解精度当a/c＞ 1 时变差.这与Orynyak-Borodii 点载荷权函数法的情况类似, 可能也是因为只用了1 项修正系数N1. 在计算效率方面, Orynyak-Borodii 法优于Wang-Glinka 法. 这主要是因为在后者的计算中, 加载点P(x,y)到裂纹前缘的最短距离s无法用初等函数表达, 只能采用数值方法, 所需计算时间较多.这种方法还有待作更广泛深入的研究和比较.

4.2.3 McClung-Lee 双变应力场点载荷权函数法

McClung 及其合作者(McClung et al. 2004, 2008, 2013; Lee et al. 2008; Sobotka & McClung 2019)以Orynyak 和 Borodii (1995)的PWFM 点载荷权函数为基础, 提出了适用于双变应力场的一种新的三维点载荷权函数表达式. 利用修正项来处理有限边界和自由表面对半椭圆表面裂纹和四分之一椭圆角裂纹的影响. 以有限板角裂纹为例, McClung 等 (2004)的点载荷权函数表达式为

式中, 多项式的系数(pi,qi,gij) 通过对无裂纹体在假想裂纹处的实际应力作回归分析确定.

针对大量的几何参数组合, McClung 团队利用边界元软件FADD3D 建立了参考载荷下的应力强度因子的数据库. 每个裂纹几何需要3 种参考应力:σ0= 1,σ1= -y/a+ 1 和σ3= -x/c+ 1.可见参考解的计算工作量很大. 通过与数值方法(FADD3D 和FEM) 结果的各种对比(见图39和图40 的示例), McClung-Lee 双变应力场点载荷权函数法得到了广泛验证(McClung et al.2013), 并已成功用于航空发动机高能涡轮部件的损伤容限分析设计软件DARWIN (2008). Sobotka 和McClung (2019)最近对该方法的求解精度和可靠性的全面验证结果表明, 90%以上的应力强度因子与有限元解的偏差不超过5%.

4.3 三维应力强度因子求解的工程简化方法

三维裂纹的应力强度因子随裂纹前缘位置变化, 其最大和最小值一般位于裂纹最深点和表面点. 为降低三维裂纹问题的求解难度, 工程中采用各种简化处理方法计算这两个点的K值. 应用较为广泛的2 种方法是: (1) 由Glinka 团队提出的三维裂纹最深点和表面点K值的通用权函数法; (2) 裂纹前缘应力强度因子的局部加权平均法. 这两种方法在理论基础、求解精度以及适用范围等方面存在明显局限性. 但由于使用方便, 在工程中有较多应用.

4.3.1 Glinka-Shen 通用权函数法

Glinka 研究团队(Shen & Glinka 1991, Glinka 1996, Zheng et al. 1996, Kiciak et al. 1998)把其二维裂纹通用权函数法直接用于三维表面裂纹和角裂纹最深点(A)和表面点(B)应力强度因子的求解. 图41 表示平板半椭圆表面裂纹和四分之一椭圆角裂纹A和B两点的权函数mA和mB的相关几何参数.

最深点A

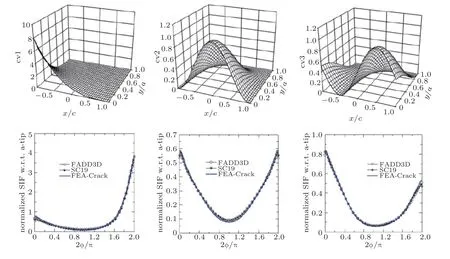
图39有限板半椭圆表面裂纹在3 种双变应力作用下的无量纲应力强度因子3 种解法的结果比较. 点载荷权函数法, 边界元数值法- FADD3D, 有限元法- FEACrack (McClung et al. 2013)

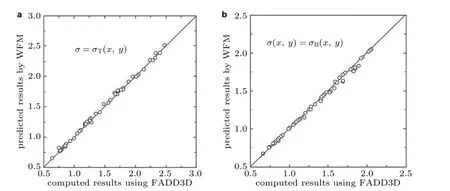
图40点载荷权函数法(PWFM)与边界元法(FADD3D)计算的孔边角裂纹无量纲应力强度因子比较.(a) 拉伸, (b) 弯曲 (McClung et al. 2013)

对于表面点B, 由于裂纹尖端应力奇异性消失, 附加求解条件为权函数mB在x=a处为0.

图41平板三维裂纹权函数的参数定义. (a) 半椭圆表面裂纹, (b) 四分之一椭圆角裂纹 (Zheng et al.1996)

三维裂纹在均匀拉伸和线性变化等载荷条件下的应力强度因子参考解可从文献中查得或用三维数值方法(有限元, 边界元等)计算. 由此确定权函数(系数M1,2,3A,B)后,在沿x方向变化的应力作用下,A点和B点的应力强度因子可通过积分得到.

这种方法使用简单,被美国石油协会规范API 579 (2010)采用. 但有些问题值得注意. 如:只适用于沿x方向变化的应力情况; 表面点B的权函数为0 的条件合理性问题; 裂纹嘴x= 0 处的几何条件(一阶或二阶)导数为0 条件的使用有随意性问题; 角裂纹的A(x=a)和B(y=c)两个点都位于平板表面, 但却分别定义为最深点和表面点, 采用不同的附加条件确定其权函数, 其合理性存在疑问. 精度评价中均采用了与参考载荷区别不大的幂律应力分布(仅幂次数不同). 这种做法可能会影响评价结论的正确性.

4.3.2 局部加权平均法

另一个工程简化处理方法是计算A,B两点的应力强度因子局部加权平均值. 把半椭圆表面裂纹的扩展方式简化成只具有两个自由度的模型. 类似于二维问题, 若已知在某参考载荷σ0(x,y)作用下的应力强度因子KA0和KB0, 其定义为 (Cruse & Besuner 1975)

上式中的权函数(mA,mB)可通过将参考载荷作用下的裂纹面位移U0对裂纹尺寸a,c分别求偏导数得到其中的裂纹面位移U0可利用二维中心裂纹和边缘裂纹的裂纹面张开位移表达式以及两组正交切片的变形协调条件求得(Xu & Wu 1989). 所以只要有参考载荷作用下的无量纲应力强度因子就能够得到计算表面裂纹两个端点K¯A和K¯B局部加权平均值的权函数. Xu 和Wu (1989)用这种方法求得了圆筒内壁表面裂纹在热冲击应力下的大量应力强度因子.

4.4 小结

本节主要介绍了两类三维裂纹权函数法: 片条合成权函数法和点载荷权函数法. 这些方法各有特点, 也都得到了程度不同的应用. 可从以下3 个方面对它们作初步比较:

(1) 输入条件要求和计算量. 片条合成权函数法由于以二维解析权函数为基础, 在大多数情况下不需要三维参考解, 计算效率高. 各种点载荷权函数法则需要大量三维参考解来标定其修正系数, 计算量很大.

(2) 求解精度和方法的成熟度. Zhao-Wu-Yan 片条合成权函数法和McClung-Lee 双变应力场点载荷权函数法的求解精度都已通过与各种数值解法大量结果的对比, 得到了相当广泛的验证,方法较为成熟. Wang-Glinka 点载荷权函数法尚待更广泛的验证.

(3) 对复杂载荷的适应性. 点载荷权函数法对复杂载荷的适应性很强. 片条合成权函数法适用于两个方向独立变化的双变应力场情况, 但对于带有xmyn交叉项的双变应力场的适用性尚需更多验证.

有别于二维裂纹问题分析的权函数精度验证, 三维裂纹权函数的精度验证只能采用某些载荷情况下的应力强度因子, 评价结论与所取载荷情况有关. 能否采用类似于二维权函数的格林函数验证尚待探索. 各种三维权函数法也有待更全面的综合分析比较.

大量三维裂纹问题分析计算表明, 与三维裂纹应力强度因子的各种数值方法比较, 三维权函数法的求解精度与有限元/边界元等数值方法处于相同水平, 但计算速度则比数值方法高出2 ～4 个数量级. 这应该是权函数法在国际航空航天结构损伤容限设计工业软件中(NASGRO 2012,DARWIN 2008)发挥着关键作用的根本原因.

5 规范化解析权函数法在裂纹问题分析中的各种应用

权函数法为裂纹体关键断裂力学参量分析提供了强有力的解析求解工具. 本节简单介绍规范化解析权函数法在二维裂纹问题分析中的各种应用, 包括: 任意受载(尤其是复杂热应力和残余应力载荷)裂纹体的应力强度因子求解, 裂纹张开位移和张开面积计算, 内聚力/桥连和裂纹闭合模型的权函数分析, 共线多裂纹板(飞机结构多位置损伤MSD)的断裂力学参数分析与剩余强度预测, 用逆向权函数法求解裂纹面应力分布, 以及复杂裂纹体断裂分析的替代几何权函数解法.

5.1 任意载荷下的应力强度因子求解

任意载荷下的裂纹体应力强度因子求解是权函数法最主要的应用. 求解需要的两个条件是:

(1) 要求解的裂纹体高精度权函数m(α,ξ/α). 各种裂纹几何的m(α,ξ/α)可查阅国内外相关期刊、专著和研究报告. 汇集了各种权函数的国内外文献有: Wu 和 Carlsson (1991), 中国航空研究院主编的应力强度因子手册(1993); Glinka 1996; Fett 和 Munz (1997); Fett (2008); 吴学仁等(2019); Wu 和 Xu (2022). 需要时也可用本文介绍的各种方法推导. 采用的m(α,ξ/α)精度应满足要求, 建议尽量用可靠的格林函数而不是用某些载荷情况下的应力强度因子作为验证依据.

(2) 裂纹体受内外载荷引起的裂纹面应力分布σ(ξ). 采用弹性力学和有限元等数值方法获得,注意应确保σ(ξ)及其拟合表达式的精度.

有了高精度的m(α,ξ/α)和σ(ξ), 则通过一个简单的积分就能得到K值

对于变化剧烈的应力分布σ(ξ), 上式积分可能难以得到封闭解, 此时应采用数值积分. 文献中有多种处理被积函数在裂纹尖端的奇异性的方法 (John et al. 1995, Jones 1998, Mawatari &Nelson 2011). 目前MATLAB 等软件也能方便地处理积分奇异性问题. 2.1.1.3 节给出了裂纹面3种基本载荷情况下的f(α)解析表达式. 对于多项式σ(ξ)情况, 利用幂函数σ(ξ)的fn公式和表格值, 能快速得到f(α). 如果σ(ξ)难以用多项式表达, 则可利用线性分段处理后求和的方法快捷求得f(α). 与数值方法一次建模计算只能得到一个α在一种载荷条件下的单个f值相比, 权函数法给出的积分结果是函数f(α). 其计算效率可比数值方法高出几个数量级. 图42 是用规范化解析权函数计算得到的不同跨宽比(s/W)的三点弯曲试样和不同载荷偏心距(d/W)的C 形试样的无量纲应力强度因子. 图43 是用规范化解析权函数法计算得到的圆盘单/双边缘裂纹在一对径向集中力作用下的II 型无量纲应力强度因子. 这些结果与文献解和有限元解均高度符合(Xu et al.2020a, Wu & Xu 2022).

热应力和残余应力是裂纹体载荷复杂多变性的典型例子. 这两类应力不但变化剧烈, 而且还受到多个参数的影响, 如热冲击应力随时间变化, 残余应力随工艺参数变化等. 图44 是文献中一些代表性热应力和残余应力分布曲线, 相关的应力强度因子求解远比机械载荷情况复杂. 若采用有限元等数值方法对许多裂纹长度/多种应力分布情况作计算, 工作量会很大. 这也是文献中对这类裂纹问题的分析计算基本上都采用权函数/格林函数法(包括由权函数法派生的多项式法)的根本原因. Heaton (1976)和Parker (1982)已证明, Bueckner (1958)叠加原理与裂纹面应力的来源无关. 把叠加原理推广到热应力和残余应力裂纹问题, 不需要考虑因引入裂纹使原来的自平衡内应力场发生改变的问题, 而只要把无裂纹体在初始状态下的内应力分布直接作为裂纹面应力σ(x), 再对等效裂纹问题进行断裂力学分析.

图42两种试样的正则化应力强度因子. (a) 不同跨宽比的三点弯曲试样, (b) 不同载荷偏心距的C 形试样

图43含单/双边缘裂纹圆盘在一对径向集中力P 作用下的II 型无量纲应力强度因子: 规范化解析权函数解与有限元解的比较. (a) 单裂纹, (b) 双裂纹 (Xu et al. 2020a; Wu & Xu 2022)

作为示例, 图45 是用解析权函数法得到的有限板边缘裂纹的热冲击应力强度因子. 图46 是两种试样的残余应力及其对应的残余强度因子, 其中(a)是Ribeiro 和Hill (2016)用Wu-Carlsson 解析权函数法得到的有限板边缘裂纹激光热冲击残余应力强度因子及比较, 二者高度符合(注意图中a/W＞ 0.85 超出了Wu-Carlsson 权函数的适用范围); (b)是无限板冷挤压孔的残余应力(实线)和用解析权函数法得到的不同挤压量孔边裂纹的应力强度因子(虚线). 这两个图中有一个规律值得注意: 当裂纹长度接近于裂纹体的韧带宽度时,K趋于0. 这是自平衡应力场引起的应力强度因子的固有规律. Wu (1991a)已证明, 对于自平衡应力场中的裂纹, 当裂纹长度接近韧带宽度时其K值必将趋于0.

图44典型热应力和残余应力分布. (a) 圆柱体热冲击应力, (b) 冷挤压孔边残余应力, (c) 飞机机翼铝合金锻件的简化残余应力, (d) 圆管焊缝轴向残余应力 (吴学仁等 2019)

文献中还有一种专为求解热应力场裂纹应力强度因子的热权函数 (thermal weight function,TWF) (Tsai & Ma 1992, Lu et al. 2001). TWF 仅取决于裂纹体几何构型而与温度及其梯度无关, 用于求解任意温度场中的裂纹应力强度因子. 由于只需对热权函数与温度/温度梯度的乘积作积分, 所以能大大提高热冲击裂纹问题的求解效率. 但TWF 只能用于热应力裂纹问题.

用权函数法求解热应力/残余应力场裂纹问题的大量实例可见文献(Parker 1982, Oliveira &Wu 1987, Bahr et al. 1987, Schneider & Danzer 1989, 吴学仁 1989, Wu & Carlsson 1991,Schneider & Petzow 1991, Wu 1993, Fitzpatrick & Edwards 1998, Liu et al. 2000, Lim et al. 2003,Zhang et al. 2009, Zhou 2003, Stefanescu 2004, Bao et al. 2010, Ribeiro & Hill 2016, Kuutti &Virkkunen 2019).

图45有限宽板边缘裂纹. (a) 热冲击应力分布, (b) 热冲击应力强度因子

图46两种残余应力场作用下的无量纲应力强度因子. (a) 有限宽板激光冲击残余应力和三种方法计算的边缘裂纹K 结果的比较 (Ribeiro & Hill 2016), (b) 无限板冷挤压孔的残余应力(虚线)和不同挤压量孔边裂纹的K

合理考虑各种工艺导致的构件残余应力对于保证工程结构完整性具有重要意义. 美国洛克希德-马丁公司在其联合攻击机的损伤容限设计中, 考虑关键结构锻件残余应力对疲劳裂纹扩展寿命的影响 (Ball 2008, Ball & Watton 2011, Ball et al. 2014), 利用文献中的权函数/格林函数(Tada et al. 1985, Wu & Carlsson 1991, Fett & Munz 1997)对飞机翼梁大型铝合金锻件多达970个控制部位进行了损伤容限分析. 结果表明, 通过考虑锻造残余应力对疲劳裂纹扩展的影响, 能减少其中930 个部位的厚度0 ～ 20%, 使结构显著减重, 如图47 所示(Ball 2008).

图47权函数/格林函数法在洛-马公司联合攻击机含残余应力的机翼梁锻件损伤容限设计中的应用成效. (a) 最终设计许用应力与基线设计许用应力的比值, (b) 因许用应力提高导致的翼梁970 个控制部位的局部厚度相对变化(Ball 2008)

水力压裂/水压致裂(hydraulic fracturing)是很多工程领域关注的共性问题. 水压诱发的裂纹扩展对各类岩体工程(如油气开采、水库大坝和矿井安全、水压诱发工程灾害防治、核废料地下储存、地热开发等)具有重要理论意义和应用价值. 水压下工作的混凝土构件必须考虑水压对裂纹的影响(徐世烺和王建敏 2009). 油气开采中的水力压裂分析需要考虑裂纹和射孔及井筒的影响(唐世斌等 2017). 图48 所示为典型的孔边裂纹问题(张开/剪切-I/II 复合型), 受载情况复杂, 涉及到远场地应力、时间相关流体压力 (李宗利等 2005), 以及断裂过程区的内聚力; 所关注的断裂参量除应力强度因子KI和KII外, 还可能有裂纹张开位移COD 和张开面积COA; 对于实验室试样还应该考虑有限尺寸的影响(Chen et al. 2017, 刘正和等 2019). 虽然采用有限元/扩展有限元(FEM, XFEM)等数值方法分析这些问题在技术上完全可行, 见图49 (Wang et al.2015), 但由于需要考虑的参数很多, 工作量很大, 时间成本很高. 而采用权函数法则可大大提高求解效率, 并易于进行参量分析(Garagash & Detournay 1997, Dong et al. 2018).

5.2 裂纹张开位移和张开面积计算

权函数除了用于应力强度因子的高效计算外, 还可通过以下积分快速求得裂纹张开位移COD, 即

把中心裂纹和边缘裂纹的规范化解析权函数m(α,ξ/α)公式分别代入式(86), 则有

中心裂纹

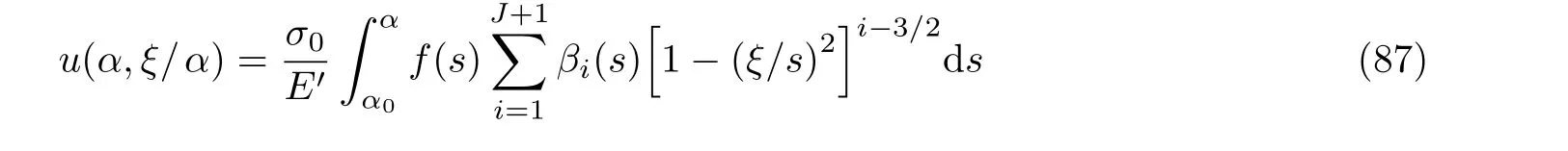
边缘裂纹

图48(a) 内聚力水力压裂模型(刘曰武等 2019, Chen 2012), (b) 孔边裂纹水力压裂分析模型(Dong et al. 2018)

图49混凝土重力大坝高压水劈裂分析模型. (a) 扩展有限元模型(XFEM), (b) 裂纹面水压分布(Wang et al. 2015)

在断裂力学参量的实验测定中, 常利用柔度关系式确定裂纹长度. 计算中需要裂纹嘴的张开位移CMOD:u(α,ξ/α= 0). 因ξ/α= 0, 式(87)和式(88)简化为:

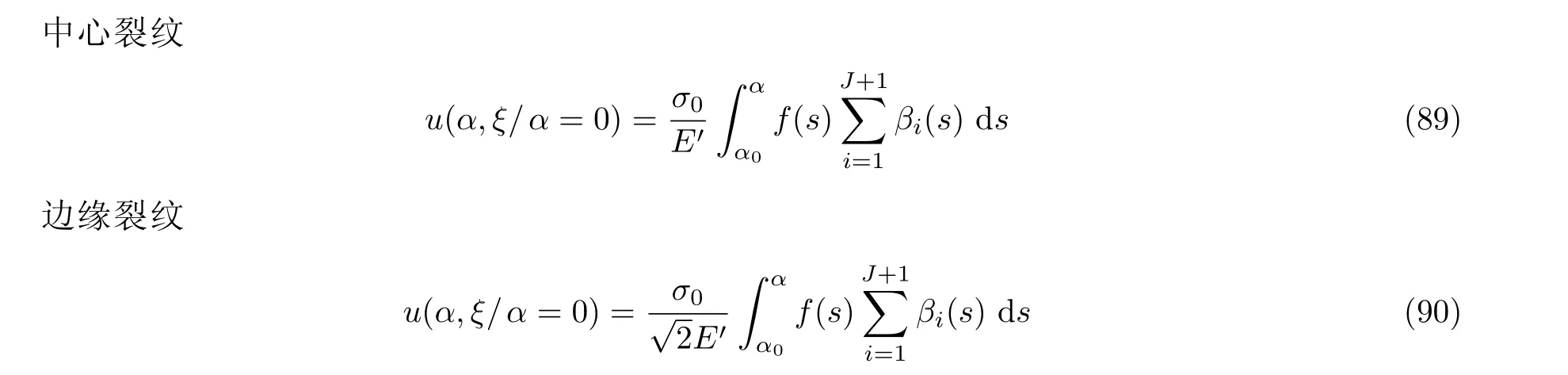
式中f(s)是无量纲应力强度因子. 计算COD 时可把裂纹面载荷情况分为图50 所示3 种形式.

图50裂纹面的3 类载荷形式. (a) 整个裂纹面受连续分布应力, (b) 裂纹尖端后方部分裂纹面受均匀应力, (c) 裂纹面任意位置受集中力

整个裂纹面受均布/非均布连续分布应力下的COD 可参见2.1.1 节图3. 图51 是有限宽板中心裂纹和边缘裂纹在裂纹面任意位置受区段均布应力作用下的COD 示例. 图52 是有限宽板中心裂纹和圆盘边缘裂纹在裂纹面一对集中力作用下的COD 示例(α= 0.5). 可见中心裂纹和边缘裂纹的COD 有显著差别, 特别是当无量纲裂纹长度较大时.

用规范化解析权函数求解得到的裂纹张开位移具有很高的精度. 各种裂纹几何/载荷下的COD 精度已得到广泛验证(童第华和吴学仁 2013, Tong & Wu 2015, 吴学仁等 2019). 图53 是Ribeiro 和Hill (2016)用Wu-Carlsson (1991)权函数法得到的有限板边缘裂纹在剧烈变化的激光冲击残余应力场作用下的COD 结果 (a/W= 0.25, 0.6), 解析权函数与有限元两种方法的计算结果高度一致. 有关用规范化解析权函数法计算COD 的具体细节可见文献(Wu & Carlsson 1991,吴学仁等 2019, Wu & Xu 2022).

对解析权函数法得到的裂纹张开位移u(α,ξ/α)沿裂纹长度积分, 可直接得到裂纹张开面积(crack opening area, COA).

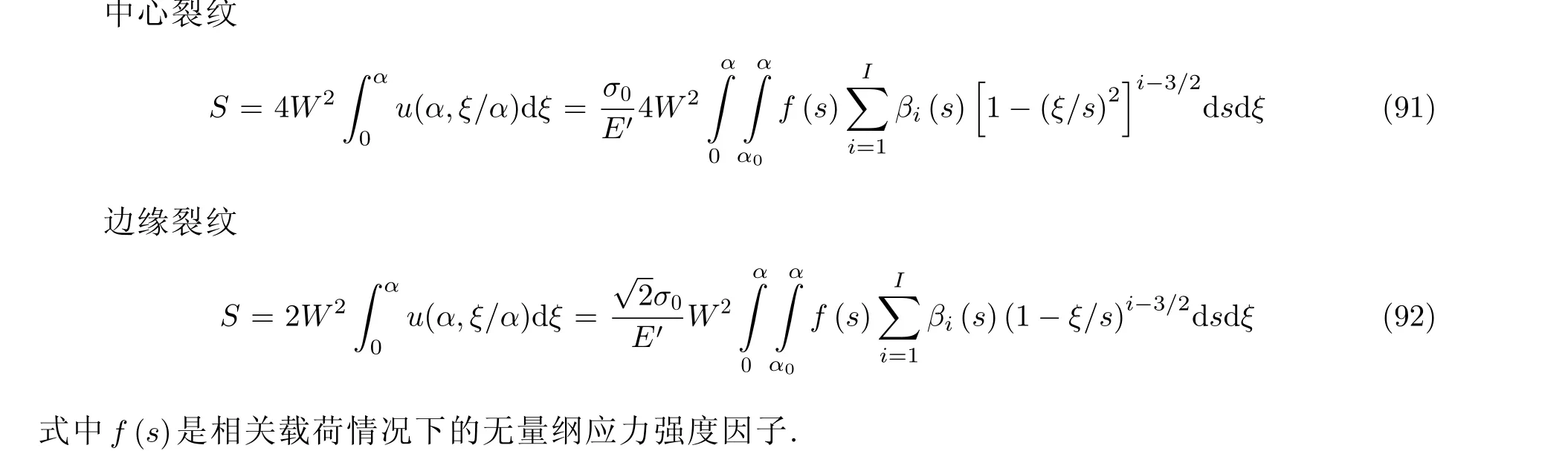
5.3 内聚力/桥连和裂纹闭合模型的权函数法求解

以上两节用权函数法分析的裂纹问题, 考虑的是外载荷和热应力及残余应力. 本节简单介绍权函数法在直接作用于裂纹面的几种载荷情况下的断裂力学分析中的应用, 包括桥连应力(bridging stress), 内(黏)聚力(cohesive stress), 以及疲劳裂纹扩展寿命预测模型中的裂纹闭合/张开应力(closure/opening stress). 这些载荷情况与各类材料的裂纹分析建模密切相关, 包括近来迅速发展的各种新型材料: 智能/纳米/生物/石墨烯材料.

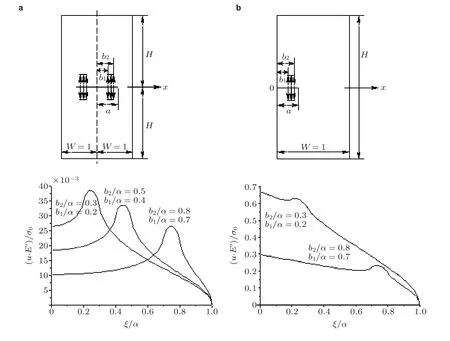
图51有限宽板受裂纹面区段均布应力作用的COD (α = 0.5). (a) 中心裂纹, (b) 边缘裂纹

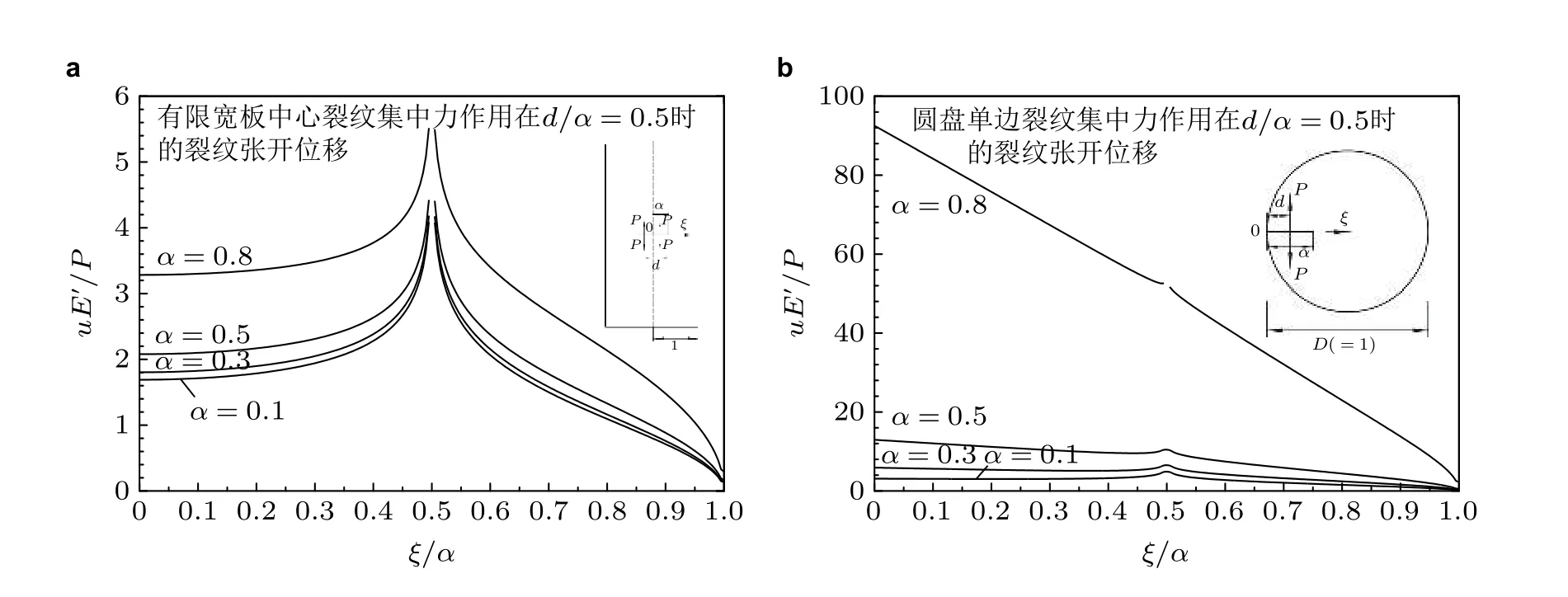
图52裂纹面一对集中力作用下的COD (d/α = 0.5). (a) 有限板中心裂纹, (b) 圆盘边缘裂纹

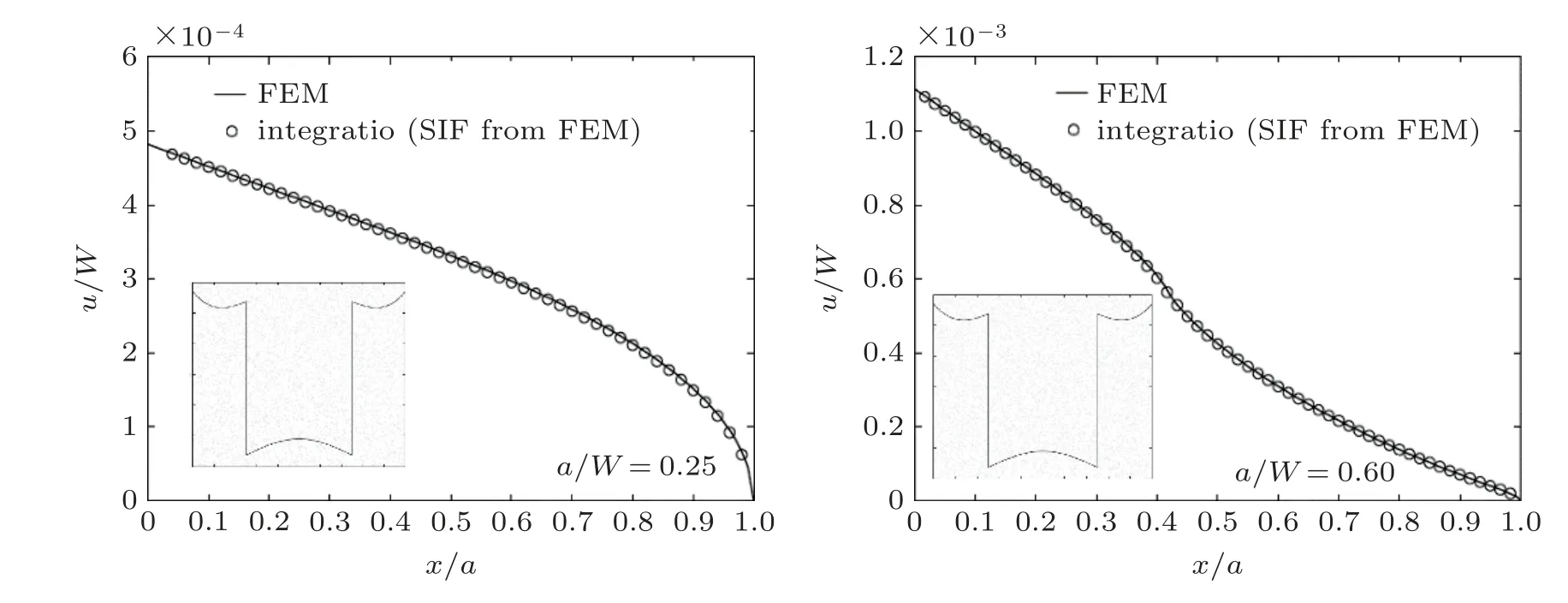
图53在激光冲击导致的剧烈变化残余应力作用下, 有限宽板边缘裂纹张开位移的解析权函数解与有限元结果比较(a/W = 0.25, 0.6). 图中左下方的插图是残余应力分布 (Ribeiro & Hill 2016)

桥连(bridging)是材料增韧的一种主要机制, 桥连应力的确定以及桥连对裂纹扩展和剩余强度影响的量化分析是评价桥连效应的关键; 内聚力模型(cohesive zone model)是研究裂纹尖端损伤和预测剩余强度最常用的模型之一, 广泛应用于各类金属、复合材料以及岩土等材料与结构的破坏分析; 对于变幅载荷下的金属材料疲劳裂纹扩展而言, 考虑疲劳裂纹尾迹残余塑性变形影响的裂纹张开/闭合应力分析是寿命预测的关键环节; 在混凝土等准脆性材料的断裂研究中, 裂纹尖端后方的黏聚应力引起的黏聚应力强度因子计算则是确定混凝土双K断裂韧度的核心. 尽管桥连裂纹模型、内聚力模型和基于塑性诱导的裂纹闭合模型, 其原理和应用领域各不相同, 但它们的数学本质是相似的. 其关键环节是准确计算以裂纹面集中力和各种分布应力为代表的桥连应力, 以及内聚力/黏聚力和裂纹闭合/张开应力作用下的应力强度因子K和裂纹张开位移COD, 而它们都与裂纹几何紧密相关, 所以各种裂纹几何的权函数是建模分析的先决条件, 见5.1 和5.2 节. 用有限元等数值方法求解这些问题虽没有技术上的困难, 但建模和计算成本很高.权函数法则为这些模型分析提供了高效的解析工具.

5.3.1 内聚力模型和桥连裂纹模型的权函数法求解

利用纤维或延性颗粒的桥连机制, 能有效提高脆性基体材料的韧性. 桥连不但会影响裂纹尖端过程区内微裂纹的连通和扩展, 而且在宏观裂纹尾迹区的纤维或增强颗粒会阻碍裂纹的张开和扩展, 从而降低裂纹扩展速率, 提高材料的抗裂纹扩展能力和断裂韧性.

目前主要有两种方法用于分析材料的桥连行为. 一种是桥连裂纹模型(Cox & Marshall 1991a), 另一种是由Dugdale (1960)和Barenblatt (1962)提出的内聚力模型, 这两个模型也可以合成一个考虑(Carpinteri & Massabo 1996). 图54 是这两个模型的示意图. 桥连裂纹模型认为裂纹尖端后方的交错纤维或增强颗粒会降低裂纹尖端的驱动力-应力强度因子, 物理裂纹尖端存在应力奇异性. 内聚力模型则认为虚拟裂纹尖端的尾迹存在过程区, 虚拟裂纹尖端的应力奇异性消失, 但过程区的大小和应力分布受桥连的影响. 这两个模型都被广泛用于碳纤维树脂基复合材料、混凝土、钢筋混凝土、粗晶陶瓷、Glare 纤维金属层板和裂纹体的补强修复等材料与结构的疲劳裂纹扩展和断裂分析.

图54用于分析桥连作用的两个主要模型, a0 为初始裂纹长度. (a) 桥连裂纹模型, (b) 内聚力模型

权函数法对桥连应力作用下的裂纹问题的求解有独特优势. 用权函数法解析求解桥连裂纹模型或内聚力模型, 能方便地预测含裂纹的桥连材料和结构的剩余强度、裂纹扩展阻力R-曲线和尺寸效应. 这方面的文献很多, 如: (Carpinteri & Massabo 1996; Cox & Marshall 1991a, 1991b;Cardona et al. 1993; Bazant & Planas 1997; Buchanan et al. 1997; Wu & Bowen 2000; Fleck et al. 1996; Sivashanker 1998; Ostlund & Nilsson 1993; Ostlund 1995; Ostlund & Karenlamp 2001;Lindhagen et al 2000; Li et al. 1998; Zhang et al 2011; Zhang & Li 2004; Kumar & Barai 2011; 徐世烺 2011). 权函数法成功应用于纤维金属层板疲劳裂纹扩展寿命分析的相关研究可见文献(Guo & Wu 1998, 1999; 吴学仁和郭亚军 1999a, 1999b; Alderlisten 2007; Chang et al. 2011) 需要注意的是, 文献中对桥连分析所采用的权函数(Tada et al. 1973, 1985; Wu & Carlsson 1991;Glinka & Shen 1991; Fett & Munz 1997)精度差别较大, 故应该谨慎考虑所得结果的可靠性.

内聚力模型认为, 裂纹在外载荷和裂纹尖端过程区桥连应力共同作用下, 虚拟裂纹尖端的应力强度因子为零. 当物理裂纹尖端的张开位移达到临界值δc时, 裂纹发生扩展. 即

桥连裂纹模型认为, 当裂纹在外载荷和裂纹面桥连应力共同作用下, 裂纹尖端的应力强度因子达到材料的断裂韧度Kc则裂纹发生扩展. 其数学表达式为

式中Kp和Kb分别是外载荷P和桥连应力σb(x)作用下裂纹尖端的应力强度因子, 可方便地用权函数法求得, 见5.1 节.Kc为材料的断裂韧度,δc为材料的临界张开位移;a0和a分别为物理和虚拟裂纹的长度.

在内聚力/桥连模型的求解中, 外载荷P和桥连应力σb(x)联合作用下的裂纹张开位移δ(x)为式中up(a,x)为外载荷作用下的裂纹面张开位移, 5.2 节给出了用权函数计算up的方法; 方程右边第2 项是桥连应力σb(ξ)引起的裂纹张开位移, 其计算方法与up相同.m(a, x)为相关裂纹几何的权函数.

用权函数法可方便地建立求解内聚力/桥连模型的积分方程. 这两个积分方程在形式上基本一样. 不同的是, 内聚力模型的过程区是未知变量, 而桥连裂纹模型的桥连区长度是裂纹当前长度与初始长度之差, 是已知量. 求解积分方程, 即可确定过程区大小(a-a0)和桥连应力分布σb(x).式(95)表明, 各种裂纹几何的高精度权函数m(a, x)是准确求解积分方程的关键.

文献中对智能/纳米/生物/石墨烯等新型材料的增韧机理分析(Shao et al. 2012, Gao et al.2021, Meng et al. 2018, Wang et al. 2020)常采用Budiansky 和Amazigo (1989)的桥连区弹簧应力作用下的裂纹张开位移方程, 其核心要素是无限大板半无限裂纹的权函数精确解. 若要把这个Budiansky-Amazigo 模型应用于其他裂纹几何, 则相关裂纹的权函数就成为分析的前提.

对于理想塑性材料, 物理裂纹尖端前方屈服区内作用的是均布应力. 此情况即退化为Dugdale 模型. 该模型的求解是根据虚拟裂纹尖端应力强度因子为零的条件, 计算在外载荷和裂纹尾迹区段均布应力作用下的塑性区尺寸和物理裂纹尖端的张开位移. 与其他多种方法相比, 权函数法被认为是求解Dugdale 模型的最佳方法(张正国等 1998). 图56 是用规范化解析权函数法求得的远方均匀拉伸有限板中心/边缘裂纹的正则化Dugdale 塑性区尺寸. 有关细节可见文献(Wu &Carlsson 1991, Wu & Xu 2022). 关于幂强化材料的Dugdale 模型求解, 可见文献(Chen et al.1992, Daniewicz 1994). Wu 和 Knott (2001)则用权函数法对异种材料焊接接头作了Dugdale 模型分析, 并把近界面区的SIF 和COD 与强度失配系数(σy2/σy1)相关联.

5.3.2 确定桥连应力与位移关系的权函数法求解

类似于应力应变关系, 内聚力/桥连应力σb(x)与裂纹张开位移的关系(也简称为内聚力/桥连法则, bridging/cohesive law)是分析桥连/内聚力模型的前提. 但因为这种求解是一个数学上的反问题(inverse problem), 内聚力/桥连法则的直接求解很困难. 研究者们提出通过测量获得裂纹张开位移um(a, x), 再由理论分析反推得到内聚力法则. 测量得到的um(a, x)是外载荷和桥连(内聚)应力作用下的裂纹面位移up(a,x)和ub(a,x)叠加的结果,即

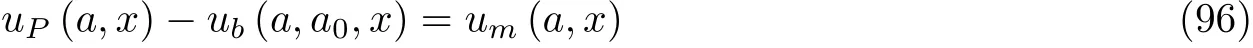
图55裂纹面受区段线性应力和两种黏聚应力分布. (a) 线性分布应力, (b) 单线性软化黏聚应力, (c)双线性软化黏聚应力

图56远方均匀拉伸有限板中心/边缘裂纹的正则化Dugdale 塑性区尺寸 ρ/(W-a). (a) 中心裂纹, (b)边缘裂纹

若已知裂纹体的权函数m(a, x), 就可方便地求解外载荷和内聚力分别作用下的裂纹面位移.外载荷作用下的up(a,x)求解见5.2 节. 桥连应力σb(x)作用下的位移ub(a,x)为

求解上述方程可得到σb(x), 进而建立σb(x)与um(a, x)的关系.

Lindhagen 等 (2000) 通过测量得到的裂纹张开位移廓线, 利用Wu-Carlsson (1991)权函数,推导出受远方拉伸的孔边裂纹的桥连律(bridging laws). Buchanan 等(1997)为求解连续纤维增强金属基复合材料(SCS-6/TIMETAL 21S)的桥连应力, 采用Wu-Carlsson (1991)规范化权函数法推导了有限宽板中心裂纹的权函数m(a,x), 并预设纤维桥连应力σb(x)的分布为

利用IDG 系统测量裂纹面多个离散点的张开位移um(a,xi), 用规范化权函数法结合最小二乘法, 求解得到预设的3 种桥连应力分布中的系数A0,A1,A2. 所得到的桥连应力与有限元计算结果吻合得很好, 见图57.

以上用权函数法求解内聚力/桥连裂纹模型、桥连应力与裂纹张开位移关系都需要反向求解积分方程. Buchanan 等(1997)的解法是预设桥连应力为某种函数形式, 通过求解桥连区内一系列位置的位移得到预设应力函数中的系数. 但若预设的函数形式不能很好地反映桥连应力的分布, 则难以得到合理的σb(x)结果. 徐武等提出了一种对连续分布的桥连应力作离散化处理的方法(即把σb(x)离散成N段应力σbi(xbi)共同作用,xbi= (xi+xi+1)/2, 每段的应力为常数), 利用权函数法成功得到了共线多裂纹屈服条带模型的韧带应力分布(徐武 2012; Xu et al. 2014), 并推广用于无限板中心裂纹的内聚力模型求解(Xu & Waas 2017), 结果如图58 所示. 与预设桥连应力分布函数的方法相比, 这种离散化处理方法更为灵活, 也可方便地用于桥连应力与张开位移关系(桥连法则)的求解.

5.3.3 塑性诱导裂纹闭合模型的权函数法求解

在材料与结构的疲劳裂纹扩展和寿命预测中, 需要考虑残留在裂纹尾迹上的塑性变形, 特别是对于变幅载荷情况. Newman (1983)基于Elber (1970)的裂纹闭合概念和Dugdale (1960)的塑性屈服模型, 提出了修正的裂纹闭合条带屈服模型, 并据此开发了变幅载荷下的疲劳裂纹扩展寿命预测软件Fastran-II (Newman 1992). Newman 模型能处理裂纹扩展的超载迟滞效应和载荷顺序等因素的影响. 其中, 各种裂纹体在不同外载荷和裂纹面任意位置窄条均布应力作用下的应力强度因子和裂纹面位移是该模型的核心要素. 这些参量都可以方便地用权函数法高效求得. 考虑塑性诱导裂纹闭合效应的裂纹扩展速率da/dN为(Elber 1970)

式中,C,n为材料常数,f为无量纲应力强度因子, ΔKeff为有效应力强度因子范围.Sop为裂纹张开应力. 各种裂纹几何/载荷的Sop高精度求解是Newman 模型成功预测疲劳寿命的关键.

应该指出, Newman 裂纹闭合模型以及裂纹张开应力方程, 原本是针对在远方拉伸无限大板中心裂纹建立的(其后扩大到孔边裂纹). 但裂纹张开应力与裂纹几何和受载情况密切相关, 所以在严格意义上, 把这两种裂纹几何-载荷情况的Sop解用于其他裂纹几何/载荷情况是不合适的.而各种裂纹体在任意载荷下的应力强度因子和裂纹张开位移都很容易用权函数法求得(见5.1和5.2 节), 因此, 权函数法为解决张开应力的几何/载荷相关性提供了方便的解析求解手段(Daniewicz & Bloom 1996). Liu 和 Wu (1997) 用Wu-Carlsson 权函数法得到了4 种有限体中心/边缘裂纹几何/载荷情况下的裂纹张开应力. Tong 和 Wu (2013, 2014, 2015)用Wu-Carlsson 权函数法改进了Newman 模型, 为不同裂纹几何的张开应力提供了高效高精度的求解方法, 并给出了半无限板边缘裂纹和孔(缺口)边裂纹的Sop方程(Tong & Wu 2014, 吴学仁等 2019). 图59 对各种方法的结果作了对比, 图59(a)表明, 用权函数法求得的受远方拉伸的半无限板边缘裂纹与中心裂纹的张开应力有明显差别. 权函数法的结果得到了McClung (1994)和Daniewicz-Bloom (1996)的有限元解的支持. 但权函数法的计算效率远高于有限元法. 图59(b)表明: 用权函数法得到的缺口/孔边裂纹在在远方拉伸下的张开应力水平与裂纹长度有关, 且在短裂纹阶段的张开应力明显低于中心裂纹(CCT), 从而导致更高的ΔKeff. 这可以在一定程度上解释为什么在相同的名义ΔK下, 短(小)裂纹的扩展速率da/dN明显高于长裂纹.

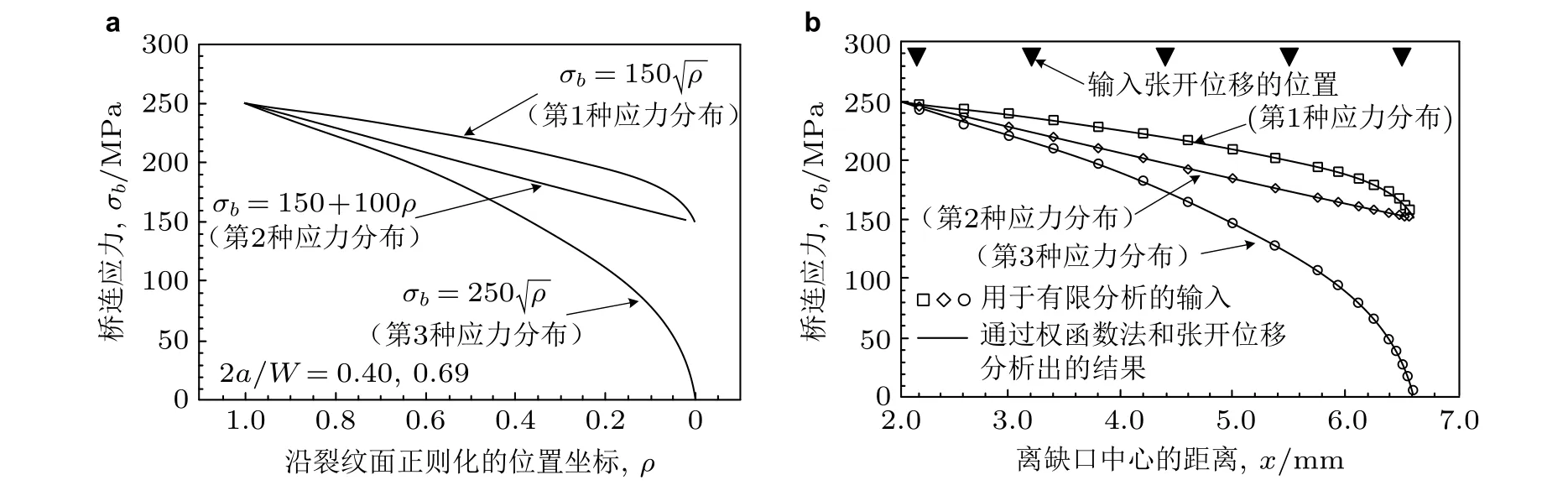
图57用权函数法得到的桥连应力结果验证 (Buchanan et al. 1997). (a) 预设的3 种桥连应力分布,(b) 采用权函数法结合最小二乘法获得的桥连应力与有限元结果的对比

图58用权函数法结合桥连应力离散化方法求得的无限板中心裂纹的内聚力模型解(Xu & Waas 2017). (a) 裂纹尖端过程区的大小及应力分布, (b) 裂纹尖端过程区内的张开位移

不少研究者用2D/3D 权函数法计算了各种裂纹几何的疲劳裂纹张开应力(Daniewicz &Aveline 2000, Ismonov & Daniewicz 2010, Daniewicz & Ismonov 2010, Kim & Lee 2000). de Matos 和 Dowell (2007)通过对有限元法和权函数法计算张开应力的比较, 认为权函数法提供了精度与所需计算能力之间的最佳平衡(weight function technique presents the best balance between accuracy and requied computing power). 利用当前文献中的权函数(Wu & Carlsson 1991; Fett &Munz 1997; Tada et al. 1985, 2000; 吴学仁等 2019; Wu & Xu 2022), 能高效求得任意裂纹几何-载荷条件下的应力强度因子和裂纹张开位移, 进而得到高精度的裂纹张开应力, 从而显著扩大Newman 裂纹闭合模型对裂纹几何-载荷条件的适用范围, 提高变幅载荷下疲劳裂纹扩展寿命预测软件的准确性.

图59用权函数法求得的几种裂纹几何的裂纹张开应力以及与有限元等数值解的比较. (a) 半无限大板边缘裂纹的裂纹张开应力(R = 0), (b) 缺口和孔边裂纹的张开应力与裂纹长度与缺口/孔半径的关系(平面应力) (吴学仁等 2019)

5.4 共线多裂纹板的断裂力学参数与剩余强度分析

利用共线多裂纹的解析权函数, 能以比有限元等数值解法高得多的效率, 计算任意载荷下含多位置损伤(MSD)板的应力强度因子, 求解Dugdale 条带屈服模型, 为剩余强度分析提供关键断裂力学参数, 从而避免数值方法的大量重复建模计算.

5.4.1 共线多裂纹应力强度因子与Dugdale 模型解

图60 给出了三条等长裂纹各裂纹中心线受一对集中力Fy作用,x0和y0表示集中力的位置.采用Love (1944)解, 可获得不含裂纹无限板受图60(a)所示3 对集中力作用下沿x轴y方向的正应力. 文献(徐武2012, Xu & Wu 2012 )利用共线裂纹的权函数法, 求得了不同裂纹间距和集中力作用位置下裂纹尖端A,B和C的应力强度因子, 如图60 所示. 为对比多裂纹间的相互影响, 图中给出了无限板单裂纹裂纹中心线受一对集中力的应力强度因子 (“◆”所示) .

图60三条等长裂纹受集中载荷及其无量纲应力强度因子解. (a) 各裂纹中心线受一对对称集中力,(b) 裂纹尖端A 的无量纲应力强度因子, (c) 裂纹尖端B 的无量纲应力强度因子, (d) 裂纹尖端C的无量纲应力强度因子 (Xu & Wu 2012)

图61 所示的载荷工况可模拟含裂纹飞机加筋蒙皮的铆钉力. 最近Zhang 等(2020)根据筋条铆钉的位移与共线多裂纹板在该处的位移相等条件, 建立并求解位移协调方程, 获得了图61(a)所示多裂纹加筋板的铆钉力, 并在此基础上采用权函数法计算裂纹尖端的应力强度因子. 图61(b)给出了中心裂纹的应力强度因子与裂纹长度关系. 为对比验证, 图中给出了Nishimura (1991)基于Fredholm 积分方程法和Collins-Cartwright(1999)采用复变函数的计算结果, 这些结果互相吻合.

图61(a) 加筋板三条对称共线裂纹受远端均匀应力, (b) 中心裂纹应力强度因子与文献结果比较(Zhang et al. 2020)

多位置损伤结构的剩余强度分析常采用Dugdale 条带屈服模型(Nilsson & Hutchinson 1994). 图62 所示部分裂纹面受均匀载荷是Dugdale 条带屈服模型一个典型载荷工况. 采用共线裂纹的权函数法可高效、高精度地获得其应力强度因子. 图62(b)和(c)给出了两条和三条对称裂纹内侧裂纹尖端A 的应力强度因子与受载长度和裂纹长度之间的关系(Xu et al 2011, Xu &Wu 2012).

Dugdale 模型实质上是两个线弹性解的叠加. 一为远端受均匀拉伸应力σ作用下的应力强度因子; 另一个是塑性区内作用大小为材料屈服应力σs的压缩应力. 二者作用下, 虚拟裂纹的应力强度因子为零. 文献(Xu et al 2011, Xu & Wu 2012)采用权函数法求解了两条和三条对称共线裂纹的条带屈服模型. 图63 给出了不同间距下两条和三条等长对称裂纹受不同载荷下的裂纹尖端塑性区尺寸与外载荷的关系曲线. 塑性区尺寸采用单一中心裂纹Dugdale 塑性区尺寸进行正则化处理. 载荷则用屈服强度进行无量化. Collins 和Cartwright (2001)采用复变应力函数法分析了两条等长共线裂纹的条带屈服模型, 结果见图63(a)的实线. 可见这两种方法的计算结果非常吻合. 如果不考虑数值运算带来的误差, 权函数法和复变应力函数法获得的解都是精确解.

5.4.2 有限板共线裂纹屈服条带模型解与剩余强度预测

对于有限板共线裂纹,其精确的解析权函数很难获得. 徐武等(2012, Xu et al. 2014)基于单一裂纹的权函数提出了共线裂纹条带屈服模型的“统一”分析方法. 这里以图64 所示有限宽板两条等长共线裂纹的条带屈服模型为例来介绍该方法. 图中裂纹长度分别为2a1和2a2, 裂纹间的韧带长度为X1. 平板远端受均匀拉伸, 从左到右裂纹尖端的塑性区尺寸和裂纹尖端张开位移分别为rA,rB和δA,δB.“统一”分析方法把裂纹及其间的韧带和塑性区连通成一条裂纹长度l=(b+ 2a+rB)的单裂纹, 如图64(b)所示, 在塑性区内和韧带上作用压缩载荷. 未知量为弹性韧带上的压缩应力σ(x)和塑性区rA和rB.

该等效的单裂纹需满足的条件为: 裂纹尖端的应力强度因子为零和弹性韧带区域x∈±[0,X1]的张开位移为零. 为获得载荷σ(x)作用下的应力强度因子和裂纹张开位移, 把连续分布应力σ(x)离散为N段均匀分布应力, 如图65 所示. 即σ(x)变成一系列未知离散值σi(i= 1, 2, …,N),σi表示裂纹面[xi,xi+1]上作用的应力. 单一等效裂纹受此复杂载荷作用下的应力强度因子和裂纹张开位移可由叠加原理求得. 其核心是获得中心裂纹部分裂纹面受均匀载荷作用下的应力强度因子f(l,x1,x2)和张开位移u(l,x1,x2,x), 它们可高精度地由有限板单一中心裂纹权函数法计算(Wu & Carlsson 1991, 吴学仁等2019).

用叠加原理求解单一等效裂纹应力强度因子K和裂纹张开位移U(l,x), 未知变量变为(N+2)个, 即:σi(i= 1, 2, …,N),rA和rB. 为确定这(N+2)个未知量, 至少要(N+2)个方程. 为此, 根据单一等效裂纹的条件, 构建如下方程组

图62(a) 两条等长裂纹, (b) 三条对称裂纹, (c) 两条等长裂纹, 内侧裂尖A 的无量纲应力强度因子,(d) 三条对称裂纹, 内侧裂尖A 的无量纲应力强度因子 (Xu et al. 2011, Xu & Wu 2012,徐武2012)

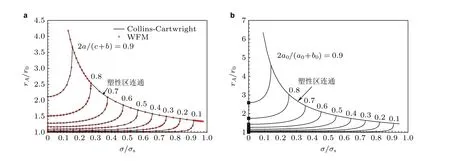
图63裂纹尖端A 的塑性区尺寸与外载荷σ/σs 关系, r0 = a0[sec(0.5πσ/σs). (a) 两条等长裂纹, (b) 三条等长裂纹(Xu et al. 2011; Xu & Wu 2012)

即, 把连续分布的应力σ(x)离散成N个均匀的应力σi, 弹性韧带上的位移为零变为弹性韧带上N个点处的位移为零. 通过增大N, 因离散而引入的近似能尽可能减小.

图64有限宽板两条等长对称裂纹条带屈服模型. (a) 条带屈服模型, (b) 一条等效的中心裂纹用于分析(a)

当塑性区连通时, 其未知量为临界载荷σc和外侧裂纹尖端的塑性区rB. 确定其方程组为

求解以上方程组, 可获得不同裂纹形态a/(a+b)受不同载荷σ/σs作用下, 裂纹尖端A 的塑性区尺寸和张开位移与外载荷的关系曲线, 如图66 所示. 图中的塑性区尺寸都除以无限板单一中心裂纹条带屈服模型的塑性区尺寸和裂纹张开位移(徐武2012, Xu et al. 2014). 为了定量分析有限边界的影响, 图66(a)的虚线给出了无限宽板两条等长共线裂纹的正则化裂纹尖端塑性区和张开位移. 可以看到: 有些情况下, 有限边界的影响较大, 不能忽略. 图66(b)给出了不同载荷下裂纹面的张开位移. 为验证其精度, 图66(b)给出了有限元法分析的裂纹张开位移. 可见这两种方法的计算结果非常吻合.

权函数法在共线多裂纹板的剩余强度分析方面也具有独特优势. 对于韧性材料的裂纹扩展,Nilsson 和Hutchinson (1994), Newman (1986) 改进了屈服条带模型, 把裂纹稳态扩展过程分成两个阶段, 裂纹起裂和稳态扩展. 在外载荷作用下, 当初始裂纹的张开位移达到某一确定临界值时裂纹起裂; 裂纹的稳态扩展通过恒定的临界裂纹张开角来描述. 即

式中δ(a, a-d)为x=a-d处的张开位移, 括号内第一个变量a表示裂纹长度, 第二个d为距裂尖的一个特定距离, 通常取1 mm.δc(a-d,a-d)为裂纹面残留塑性尾迹高度,αc为临界裂纹张开角.

图65连续分布应力作用的分析模型. (a) 部分裂纹面受连续分布应力σ(x)作用, (b)一系列离散的部分裂纹面受均匀应力作用以模拟情况(a), (c) 单一中心裂纹部分裂纹面[xi, xi+1]受均匀载荷作用

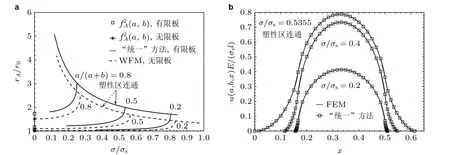
图66裂纹尖端正则化塑性区尺寸和张开位移与外载荷关系r0 = a[sec(0.5πσ/σs) - 1], δ0 =8aσs/(πE)ln[sec(0.5πσ/σs)], (2a + b)/w = 0.5. (a) 裂纹尖端A 的塑性区尺寸, (b) 裂纹张开位移, a =b = 1/6 (徐武2012, Xu et al. 2014)

为获得裂纹扩展分析中的塑性区尺寸和张开位移, 文献(徐武2012, Xu et al. 2014)采用基于权函数的“统一”方法获得有限宽板共线裂纹屈服条带模型的塑性区尺寸和张开位移, 结合裂纹张开角准则, 预测了2、3、5 和7 条裂纹在拉伸载荷下的裂纹扩展长度与载荷的关系. 预测的剩余强度与实测值吻合良好, 且权函数法优于有限元法, 如图67 所示. 一旦编写好权函数法的多位置损伤板的剩余强度求解程序, 任意裂纹构型一般2 min 可完成求解计算, 而基于弹塑性有限元的裂纹扩展分析, 在计算收敛的情况下, 也至少需要2 h. 若考虑建模时间, 权函数法的计算效率比有限元高2 个数量级. 这表明, 共线多裂纹解析权函数法能为飞机结构的MSD 损伤容限分析提供高效可靠的分析工具.

5.5 用逆向权函数法求解裂纹面应力分布

在用权函数法计算应力强度因子的式(83)中, 权函数m(α,ξ/α)为已知, 另外3 个变量/函数是: 无裂纹应力σ(ξ)/σ0、无量纲应力强度因子f(α)和裂纹张开位移u(α,ξ/α). 通常情况是由σ(ξ)/σ0和m(α,ξ/α)求f(α)和u(α,ξ/α). 这是断裂力学中的“正问题(forward problem)”. 反过来,也可由u(α,ξ/α)和m(α,ξ/α)求f(α)和σ(ξ)/σ0. 这是断裂力学中的“反(逆)问题(inverse problem)”,即权函数法的反(逆)向应用. 这里简单介绍一种由已知权函数m(α,ξ/α)和裂纹嘴张开位移CMOD, 即u(α,ξ= 0), 反向求解无裂纹应力σ(ξ)/σ0的方法(Wu & Tong 2014, 吴学仁等 2019,Wu & Xu 2022), 可为假想裂纹处的残余应力和桥连力的求解提供一种简单有效的途径.

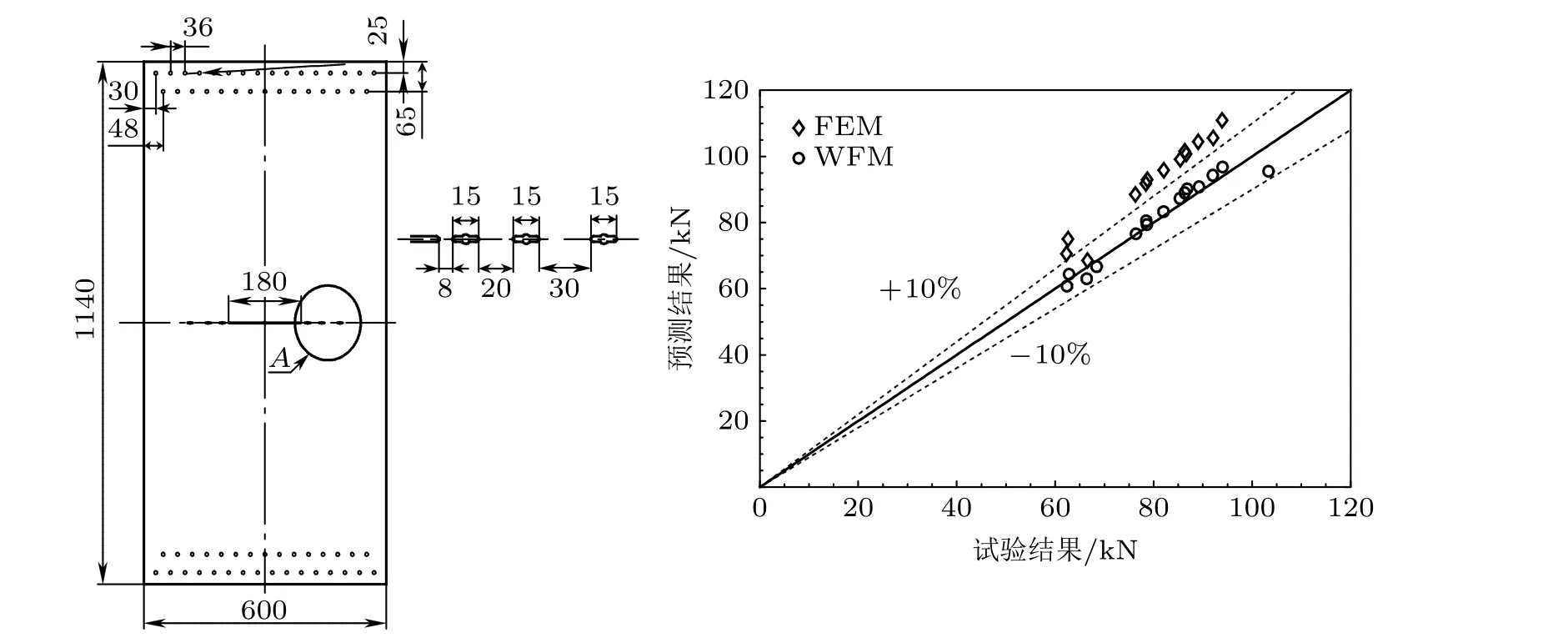
图67基于单裂纹权函数的“统一”分析方法和有限元法预测的共线多裂纹板剩余强度比较 (Xu et al.2014, 吴学仁2019)

求解时可以先把未知应力σ(ξ)/σ0预设为某个函数形式, 再反向求解确定其系数, 如Buchanan et al. (1997), 见5.3.2 节. 也可采用更灵活的分段离散化方法, 假设每个区段内的σ(ξ)/σ0值都是常数. 把最大裂纹长度αmax分割为n个等长的小区段α1,2...max, 把对应的坐标ξmax同样也分割成许多等长的小区段ξ1,2...max, 并假设每个小区段的σi为常数. 只要n足够大就能保证计算精度.将分区段离散化表达的无裂纹应力分布σi和m(α,ξ/α), 以及ui(α,ξ= 0)代入式(86), 即可建立求解σ1～σn的线性方程组.

求得每个区段的高精度数值解σ1～σn后. 合并全部n个区段就能得到σ(ξ)/σ0. 用类似的逆向权函数方法, 也可方便地由CMOD 反求得到无量纲应力强度因子f(α).

为验证逆向权函数法的有效性, 以无限大板共线裂纹的权函数精确解和周期性应力σ(ξ)/σ0=cos(2πξ)作用下的CMOD 精确解作为已知条件. 共线裂纹的权函数、裂纹嘴张开位移u(α,ξ=0)以及无量纲应力强度因子f(α)精确解分别为反向求解得到的σ(ξ)/σ0和f(α)与已知σ(ξ)/σ0=cos(2πξ) 以及f(α)的精确解几乎完全一致.

图68 是用逆向权函数法反向解得的在直径方向一对集中力作用下的无裂纹应力分布. 求解中分别以圆盘中心裂纹和圆盘边缘裂纹两种几何的解析权函数和CMOD 有限元解为已知条件.所得两种结果几乎完全一致, 并且都与集中力作用下的弹性力学精确解高度重合.

图69 是用逆向权函数法反向解得的无限大板中心裂纹的焊接残余应力分布. 以无限板中心裂纹的解析权函数和CMOD 精确解(Tada et al. 2000, Terada 1976)作为已知条件

反向求解得到的σ(ξ)/σ0结果与式(110)的残余应力精确解高度一致

该方法的更多应用示例可参阅文献(吴学仁等 2019, Wu & Xu 2022). 注意以上演示中采用的CMOD 是已知精确解或由权函数法正向求得的高精度解. 而在实际应用中则需采用实测的CMOD 数据, 它们可能受到数据噪声的干扰. 对此可采用吉红诺夫正则化方法(Tikhonov regularization method)处理. 这种逆向应用权函数由实测CMOD 反求无裂纹应力的方法有待在实际应用中验证和改进.

Cox 和 Marshall (1991b)提出了由裂纹张开位移COD 求解裂纹桥连应力的方法. Nazmul和 Matsumoto (2004, 2008a, 2008b)针对有限板边缘裂纹试样(SEN)用它求解混凝土结构中的钢筋力, 为结构健康监测(structural health monitoring, SHM)提供重要信息, 并具体讨论了用吉红诺夫正则化方法处理不适定逆问题. 本文讨论的各种裂纹几何的权函数则能为应用这些解法提供必要条件. 但应注意到, 基于COD 的解法需要以整个裂纹面的张开位移u(α,ξ/α)作为已知条件, 对输入信息的要求较高, 或可与基于CMOD 的方法形成互补.

5.6 复杂裂纹体断裂分析的替代几何权函数解法

图68用逆向权函数法解得的两种圆盘裂纹几何受一对集中力P 的无裂纹应力及与精确解比较 (吴学仁等 2019)

图69(a) 无限大板中心裂纹受焊接残余应力作用; (b) 用逆向权函数法求得的无限大板中心裂纹所受残余应力σ(ξ)/σ0, 以及与已知精确解的比较 (吴学仁等 2019)

文献中已有的解析权函数难以涵盖工程结构中的各种复杂裂纹几何, 所以寻找复杂几何裂纹体权函数的工程近似方法具有实用价值. 针对复杂裂纹体的工程分析, 研究者们提出了一种称为“替代几何(substitute geometry)”的方法(Zerbst et al. 2005, 2007; Anisworth et al. 2003; Anderson 2005; Millwater et al. 2007). 英国标准BS 7910 (2015)则称之为“等效几何”(equivalent geometry)方法. 它们都是用一个总体几何形状类似, 但局部有差异的简单裂纹体(即替代几何或等效几何), 来代替实际工程结构中的复杂裂纹体. 用权函数法求解所需替代几何的权函数m(α,ξ/α)是已知的, 而裂纹面应力σ(ξ)则需对实际复杂几何作无裂纹情况下的应力分析(一般采用有限元法)确定. 这种“替代几何”法能为工程结构中各种复杂几何的裂纹问题分析提供高效的工程近似求解手段. 它不但对复杂裂纹体的断裂力学分析计算具有重要实用价值, 而且能显著扩大已有裂纹体权函数的应用范围. 文献中有很多关于替代几何的工程处理方法的讨论, 但基本上是定性的. 图70 是紧邻裂纹的局部几何变化的两个典型示例(Zerbst et al. 2007): T 形焊接板及其替代几何-平直板, 圆筒焊接接头及其替代几何-光滑圆筒. 这两个替代几何的权函数均为已知.

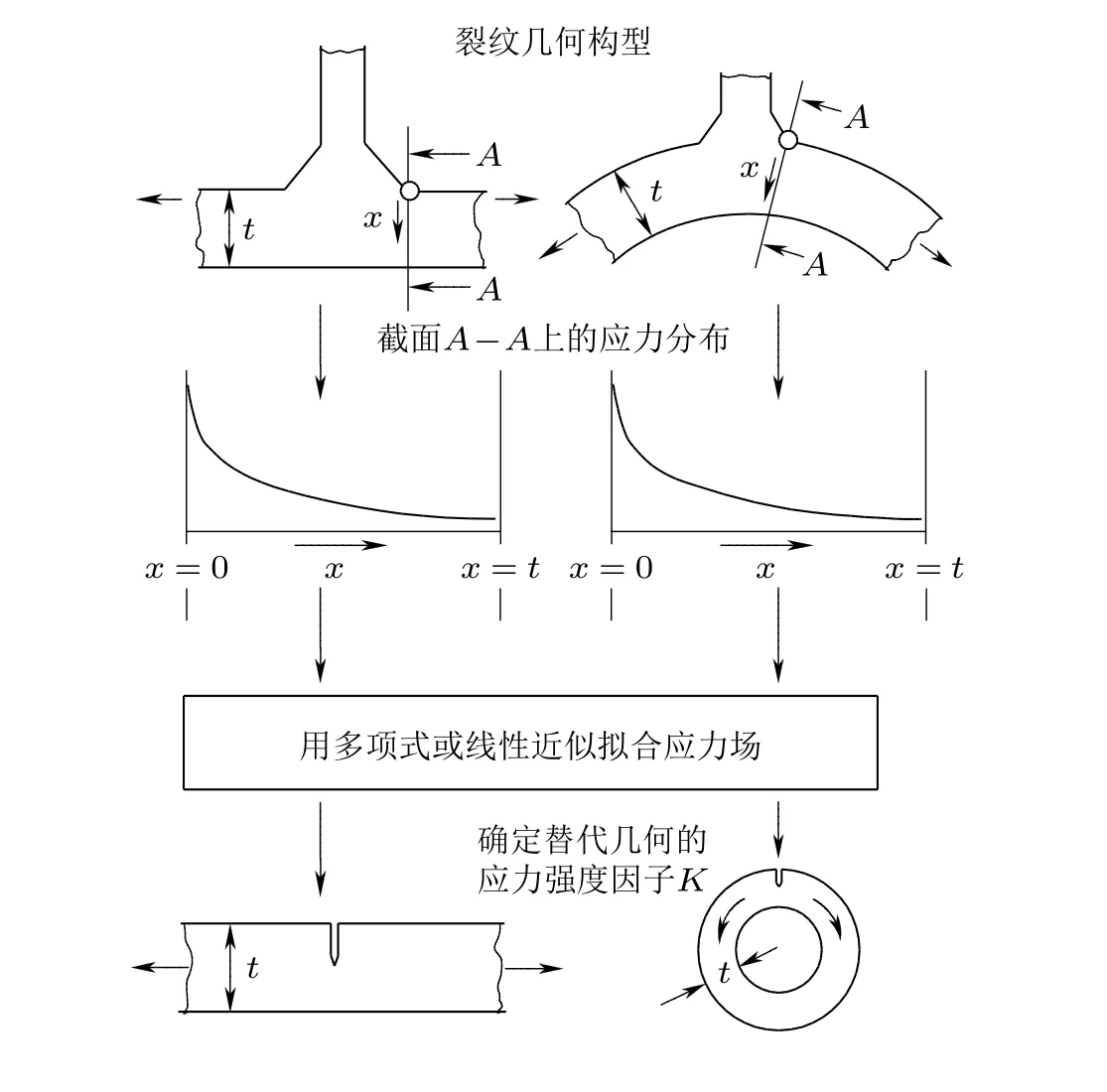
图70利用替代几何计算复杂裂纹体的应力强度因子(Zerbst et al. 2007)

吴学仁等(2019)以图71 所示的T 形焊接板及其替代几何平直板为例, 定量分析了这两种裂纹几何的权函数的差别, 并且比较不同的m(α,ξ/α)和σ(ξ)组合所得到的应力强度因子的差异. 图71(c)是两种裂纹几何的格林函数比较, 替代几何(平直板)的格林函数略高于T 形板, 但二者的差别随无量纲裂纹长度的增加而变小. Lee 等 (2006)对这两种裂纹几何的格林函数(a/W=0.3, 有限元)做过比较, 二者相当接近. 图71(d)表明, 由T 形板边缘裂纹的权函数和焊趾根部的无裂纹应力分布得到的应力强度因子(密集虚线)与有限元结果(空心圆)符合得最好. 用替代几何(平直板)边缘裂纹的权函数和T 形板焊趾根部的无裂纹应力分布得到的应力强度因子略偏高, 即略偏保守. 这为用替代几何法求解复杂结构的工程裂纹问题的合理性提供了一定程度的支持.

对复杂裂纹几何作工程断裂分析的另一种方法是Brennan 和Teh (2004)提出的权函数合成原理(weight function composition principle). 其基本思路见图72(a), 即根据两种简单几何裂纹体的已知权函数, 结合第三种裂纹几何的权函数(用有限元计算), 基于假设的权函数比例关系,确定复杂几何裂纹体的权函数. 图72(a)中的等号左右两边分别为有限板和半无限板, 其上下两边分别为有/无倾斜台阶. Brennan 和Teh (2004)假设较为复杂的带有倾斜台阶的有限板边缘裂纹与简单的有限板边缘裂纹的权函数比值与半无限板的两种相应边缘裂纹的权函数比值相等. 即

图72(a) 权函数合成原理(weight function composition principle), (b) 用合成权函数法得到的有限板半圆缺口边缘裂纹受纯弯曲的应力强度因子以及与Wu-Carlsson (1991)权函数结果比较(Brennan & Teh 2004)

图71替代几何示例. (a) T 形焊接板和平直板, (b) 远方拉伸T 形板焊趾根部的无裂纹应力分布,(c) T 形板和平直板的格林函数比较, (d) 4 种方法计算的应力强度因子及与有限元结果比较 (吴学仁等 2019)

式中,m(a,x)是权函数,a和x分别是裂纹长度和沿裂纹方向的坐标, 下标f 和s 分别表示有限板和半无限板, 上标θ表示台阶倾斜角. 用式(112)确定倾斜台阶有限板边缘裂纹的权函数, 需要知道方程右边的3 个简单裂纹几何的权函数, 但这并不容易做到. 图72(b)是用合成权函数法求得的有限板半圆缺口边缘裂纹在纯弯曲载荷下的无量纲应力强度因子与Wu-Carlsson (1991)权函数计算结果的比较, 其符合程度很好, 差别一般在2%以内.

Brennan 和 Teh (2004)把这种合成权函数法用于多种裂纹几何, 特别是含有各类缺口的边缘裂纹, 包括半圆, U 形和V 形等(Teh & Brennan 2005, 2007; Teh et al. 2006). 所得到的应力强度因子都有很好的精度. Teh (2002)通过大量有限元计算和曲线拟合建立了合成权函数的几何影响系数的数据库. Brennan 和 Teh (2004)认为, 合成权函数法排除了载荷的影响, 所以在任何载荷条件下都能够保证得到高精度的应力强度因子. 但这个结论能否普遍成立, 尚需进一步考虑以下几个方面: (1) 合成权函数法的基本公式类比关系的正确性有待更严谨的证明和广泛验证;(2) 复杂裂纹几何的合成权函数需要有3 个简单裂纹几何的权函数, 它们的精度如何保证; (3) 用一些载荷情况下的应力强度因子对合成权函数作精度验证, 不一定能全面反映权函数的真实精度. 采用格林函数作验证将会更加合理.

以上介绍的替代几何权函数法和合成权函数法在总体思路上都是把受局部几何影响较小的权函数和受局部几何影响很大的无裂纹应力分布这两个因素分离开来. 它们的区别在于确定复杂几何裂纹体权函数的具体方法. 前者的关键是替代几何的正确选择, 后者则是利用3 种裂纹几何的已知权函数合成一个新的复杂几何裂纹体的权函数. 替代几何方法把较简单的替代几何的已知权函数与实际复杂几何的无裂纹应力结合在一起, 能够为复杂几何裂纹体的断裂力学参量求解提供简单实用的手段.

6 总结与展望

权函数法是求解裂纹体断裂力学关键参量的一种高效方法. 它以灵活通用和求解效率远高于各类数值解法的特点, 为工程材料与结构的疲劳/断裂分析提供了高效可靠, 使用方便的工具.本文结合笔者及其研究团队在断裂力学权函数法方面的长期研究工作, 对半个世纪以来国际断裂界关于权函数理论与工程应用的主要研究工作作了总结/评述. 文章分为3 个部分.

第1 部分介绍了在国际断裂界广泛应用的二维裂纹问题的权函数法, 特别是Wu-Carlsson(1991)基于裂纹面位移的规范化解析权函数法, Fett(1992)和Fett-Munz(1997), 以及Glinka-Shen (1991)基于多参考载荷条件的解析权函数法; 基于裂纹面位移的规范化解析权函数法在共线裂纹、混合型裂纹和含裂纹复合材料结构方面的研究新进展. 揭示了采用应力强度因子评价权函数精度的弊端, 提出以格林函数作为评价各种权函数精度的最佳基准. 系统的对比分析表明, 基于裂纹面位移的规范化解析权函数法在精度和鲁棒性等方面明显优于基于多参考载荷条件的解析权函数法. 后者的数学本质是反向求解具有病态/不适定性的第一类伏尔特拉积分方程.

第2 部分介绍了用于内埋裂纹和部分穿透裂纹分析求解的三维权函数法, 特别是片条合成权函数法和点载荷权函数法. 片条合成权函数法的基础是二维穿透裂纹解析权函数, 所以通常不需要三维应力强度因子参考解, 对输入条件要求低, 计算效率优势明显, 求解精度可靠, 并已得到相当广泛的验证. 但片条合成三维权函数法对强双变载荷的适用性尚待进一步检验. 点载荷权函数法在对任意载荷的适应性方面具有优势, 但对于有限体的部分穿透三维裂纹几何, 点载荷权函数的确定需要多种参考载荷下的大量三维应力强度因子高精度数值解作为输入条件, 导致计算量很大. 三维裂纹权函数的精度验证目前还只能基于一些载荷情况下的应力强度因子对比. 能否采用类似于二维裂纹基于格林函数的验证途径, 尚待研究.

第3 部分简单介绍了权函数法在裂纹体分析中的各种实际应用, 包括含热冲击应力/残余应力等任意复杂载荷下的应力强度因子和裂纹张开位移计算, 多位置损伤结构的剩余强度预测, 内聚力/桥连裂纹和塑性诱导裂纹闭合等多种分析模型的求解, 由裂纹嘴张开位移通过逆向权函数法反求无裂纹构件的应力分布, 以及利用已有裂纹构型的权函数分析复杂裂纹构型的替代几何法, 以扩大已有权函数的工程应用范围. 考虑篇幅, 本文只选了一些例子来展示权函数法的多种工程应用优势. 期望能为读者解决所关心的断裂力学问题提供参考和启示.

权函数法由于计算效率高, 精度可靠(在保证权函数自身精度前提下), 从20 世纪90 年代初期就得到欧美工业界的重视, 进入实际应用, 并被各类工程结构完整性评价规范/标准/程序广泛采用(如R6 2009, BS7910, SINTAP, API2000). 进入21 世纪以来, 以NASGRO 和DARWIN 为代表的美国航空航天结构损伤容限分析大型工业软件的核心模块(裂纹驱动力计算)采用的主要(甚至唯一)方法是权函数法. 西方某航空航天公司先进战机的结构损伤容限设计大量采用了Wu-Carlsson 权函数法. 相比之下, 尽管我国在断裂力学权函数的研究方面已有了相当系统深入的积累, 但在其工程应用方面仍差距甚远. 裂纹体分析计算依赖进口软件和数值方法的局面有待改变.

对于断裂力学权函数法的未来发展, 提出以下粗浅建议.

(1) 继续扩大二维/三维裂纹几何的权函数覆盖范围, 建立经过严格验证的, 涵盖各类工业结构主要裂纹构型的权函数数据库.

(2) 在深入研究和广泛比较的基础上, 发展求解精度和计算效率更高的三维裂纹权函数法.研究三维裂纹权函数本征精度的评价验证技术.

(3) 推广断裂力学权函数法在各工业领域的工程应用, 充分利用我国学者在权函数研究方面的优势和长期积累, 联合相关研究团队, 与工业界合作开发以权函数法为核心模块, 具有自主知识产权的损伤容限设计和结构完整性评定大型工业软件和规范.

致 谢 感谢长期以来对笔者的权函数研究与应用提供指导/帮助和进行有益讨论的国内外学者,特别是A J Carlsson 先生, 黄克智先生, J C Newman Jr, T Fett, G Glinka, H R Millwater, R C McClung, M R Hill, D Ball, D P Rooke, P Bowen, R D Gregory, A P Parker 以及对权函数研究和应用作出贡献的笔者的学生/合作者: 赵伟, Oliveira, 陈晓光, 刘建中, 郭亚军, 陈勃, 童第华,景致, 赵晓辰, 刘紫璇, 饶聃钰, 张驰, 张博. 相关工作获国家自然科学基金资助(11402249,12172217).