基于熵权法的卫星钟差预报研究

梅长松， 李天智， 李 铭， 程 昊， 尹永珍， 孔祥文

(长江生态环保集团有限公司，湖北 武汉 430000)

1 引 言

卫星钟是全球导航卫星系统(global navigation satellite system, GNSS)的核心载荷之一，它的性能以及卫星钟差(satellite clock bias, SCB)预报的准确性、可靠性是影响整个系统综合定位导航授时(positioning, navigation and timing, PNT)服务能力的关键因素之一[1～7]。卫星自主导航技术需要预报一段时间的卫星星历和钟差作为先验信息以实现系统自主运行；实时精密单点定位(precise point positioning, PPP)技术需要钟差预报结果参与计算实现高精度定位；时间同步还是网络运行、节点协同的基础，是实现空间信息网络大时空跨度网络体系结构的重要保障[8,9]。因此，有必要对钟差的精确、可靠预报技术开展研究。

原子钟在卫星高速运动过程中，易受到外部环境及自身因素影响，很难掌握其细致变化规律，因此,建立精确原子钟运行模型十分困难，相应地导致准确预报钟差十分困难。目前，许多学者在钟差预报方面开展了深入研究，提出的预报模型主要有：二次多项式模型(quadratic polynomial model, QPM)、灰色模型(grey model, GM)、最小二乘支持向量机(least squares support vector machine, LSSVM)、自回归滑动平均(auto regressive moving average, ARMA)模型、人工神经网络(artificial neural network, ANN)模型、卡尔曼滤波(Kalman filtering, KF)模型等[9～14]。这些方法在钟差预报中取得了广泛应用，但也均有各自的局限性。近年来，许多学者开始研究稳定性更好、预报风险更小、可靠性更强的组合预报模型，并在这方面取得了许多研究成果。王继刚等基于线性组合预测的思想，提出一种修正线性组合钟差预报模型，既保证了钟差预报的可靠性，又提高了预报结果的准确性[15]。李晓宇等提出一种改进GM和ARMA的组合模型，验证其预报稳定性优于常规方法[16]。雷雨等采用谱分析模型拟合钟差序列的趋势项部分，采用LSSVM建模对随机项部分进行补偿，组合得到的预报结果优于IGU-P产品[17]。布金伟等提出修正经典权组合模型，将其应用到BDS/GPS卫星钟差组合预报中，改进了经典定权法的不足[18]。王冬霞等采用经典权法对QPM和GM进行综合，钟差预报精度约有一倍的提升[19]。

卫星钟运行环境复杂，受多种太空物理射线影响，卫星钟差数据在大部分情况下呈现出复杂变化规律，无论是对于中长期还是短期预报，单一预报模型都难以胜任钟差的精密预报工作。因此，结合各模型的优势和特点，探索适应能力更强、稳定性更高、预报效果更好的组合预报模型是未来钟差预报研究领域的重要方向。本文针对钟差组合预报中子模型权值难以确定的问题，将熵权法引入到BDS卫星钟差组合预报中，以GM和QPM为子模型，建立了BDS卫星钟差熵权组合预报模型。使用武汉大学IGS数据中心发布的BDS精密钟差产品，分别进行了连续多天的短期和中长期预报试验，多天的平均试验结果验证了熵权组合模型在BDS卫星钟差预报稳定性方面的优势。

2 模型原理

采用加权平均值的方法综合各子模型的钟差预报结果，通过一定的评价标准赋予不同子模型相应的权值，取加权后的结果作为组合预报的最终结果。这种方式降低了预测中的风险，其中，子模型权值的确定是关键环节。本节首先介绍几种常见定权方法，包括经典权法、修正线性组合权法，然后详细介绍熵权组合模型在钟差预报中的应用步骤。

2.1 基于经典权法的组合预报模型

假设有m个子模型参与组合预报，则组合模型预报结果的数学表达式为：

(1)

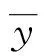
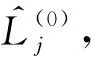
(2)

该方法仅靠拟合效果这一指标去评定各子模型的优劣，在实际过程中，可以发现有些模型拟合效果与预报效果的正相关性不强，此时经典权值的参考意义变差。

2.2 修正线性组合预报模型

针对经典权法的不足，有学者提出，在进行连续多时段预报时，可以用历史时段的预报精度来修正当前的组合权值，这种方式可以改善仅依靠模型拟合精度定权的不足[18]。具体修正原理如下：

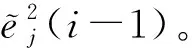
(3)

(4)

根据式(4)得到各子模型修正权值，再根据式(1)即可得到修正线性组合模型的预报结果。

2.3 熵权组合预报模型

信息熵最早是从热力学中借用过来的概念，将其作为一个随机事件的发生不确定性或者反映出的信息量的一种度量指标。一般地，信息熵值越大，认为信号中反映出的信息混乱程度越高，残留数据序列中的噪声也越大，信息利用率就越低。反之，信息熵值越小，信息利用率也就越高。信息熵的这种特性使其可以协助人们开展预测和决策工作，熵权法便是组合预测和信息熵理论的结合。

用熵权法确定组合模型权系数的步骤如下：

假设有m个子模型参与组合预报，则组合模型预报结果的数学表达式为：

(5)

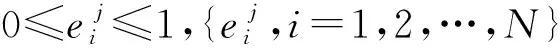
(6)

(2) 计算第j个子模型的相对误差的香农熵值为：

(7)

式中：k>0为常数； ln为自然对数；hj≥0，i=1,2,…,m。

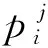
(3) 因为0≤hj≤1，根据熵值的大小与变异程度成反比的原则，第j个子模型预报相对误差序列的变异程度定义为：

dj=1-hj

(8)

则第j个子模型加权系数为：

(9)

基于熵权法的组合预报模型数学表达式为：

(10)

3 算例分析

为了对比单一模型与组合模型的预报效果，本节分别从短期和中长期预报两个方面进行预报试验，考虑到试验数据的偶然性，两方面的试验均采用连续多次的形式滚动进行，取多次试验的平均结果进行分析。目前，北斗在轨运行的卫星按其轨道类型分为3类，限于篇幅限制，从中各选取两颗数据完整性最好的卫星参与试验，卫星号分别为C01(GEO)、C02(GEO)、C10(IGSO)、C13(IGSO)、C12(MEO)、C24(MEO)。在评价预报精度时，最常用的指标是外符合精度，下载武汉大学IGS数据中心发布的精密钟差产品作为算例数据，这样可以方便地得到参考真值，计算外符合精度，对各预报方法的预报结果精度评价更为客观。

3.1 短期预报

采用数据较为完整的MJD为58 594.0至 58 603.0(2019-04-21～2019-04-30)共计10天的精密钟差产品，采样间隔为5 min。先用前144个历元(时长为12 h)的钟差数据分别用QPM(体现卫星钟的物理特性)和GM建模，预报未来12 h的钟差，这样可以进行19个时段的预报试验，而且对于建模的144个钟差数据来说，既有观测值，又有两种模型的拟合值，因此可以构建组合预报模型。对选取的6颗卫星钟精密钟差的预报结果见图1。

图1 各颗卫星的短期钟差预报残差RMSE统计图Fig.1 Statistical map of short-term clock error forecast residual RMSE for each satellite

从图1中可以看出：

(1) 在试验的各时段内，组合模型的预报精度并不一定总是最好的，研究钟差组合预报的首要目标是提高钟差预报的稳定性。如果仅仅依赖于某单一模型进行钟差预报，当该模型预报误差较大时，例如C01、C02、C24号卫星用GM进行预报时，将会给GNSS应用带来较大的误差，而用组合模型的预报结果则可以大大减弱这种风险。

(2) 从C01、C02、C12、C24号卫星的试验结果可以看出，当单一模型预报精度差异较大时，组合模型的避险作用比较明显。

在C10号卫星第2时段预报试验中，GM拟合残差序列均方误差小于QPM，但预报效果却逊于QPM，经典权组合模型为GM和QPM分配的权值分别为0.82和0.18，修正组合权模型权值分配分别是0.79和0.21，熵权组合模型权值分配分别是0.58和0.42。

图2给出了C10号卫星第2时段各模型的预报误差曲线。

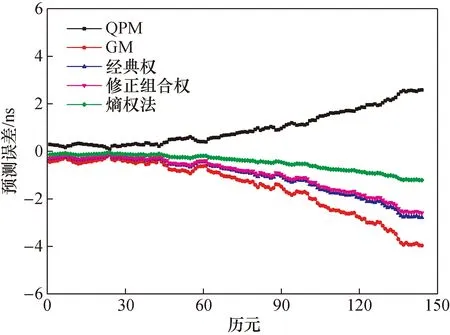
图2 C10号卫星第2时段预报残差图Fig.2 Forecast residuals for the second period of the C10 satellite

从图2中可以看出：

(1) 经典权组合预报模型预报误差曲线与GM预报的误差曲线是非常接近的，预报精度相对较低，预报误差序列RMSE值为3.79 ns。这是因为在钟差数据建模过程中，GM的拟合效果优于QPM，从而给GM预报值分配了过高的权重，但是GM的预报精度却是较差的。而修正组合权模型由于只有1段历史时段预报误差的积累，所以修正效果很小，预报误差序列RMSE值为3.69 ns。

(2) 本次预报结果反映了经典权组合模型仅以拟合效果作为定权依据有时会出现组合无效的情况，而修正经典权组合模型则需要较多历史时段预报信息的积累，才能发挥出其修正作用。相比之下，熵权组合模型预报误差序列RMSE值为2.01 ns，预报的稳定性更好。

表1给出了3种组合预报模型19次钟差预报误差的RMSE序列的统计结果。

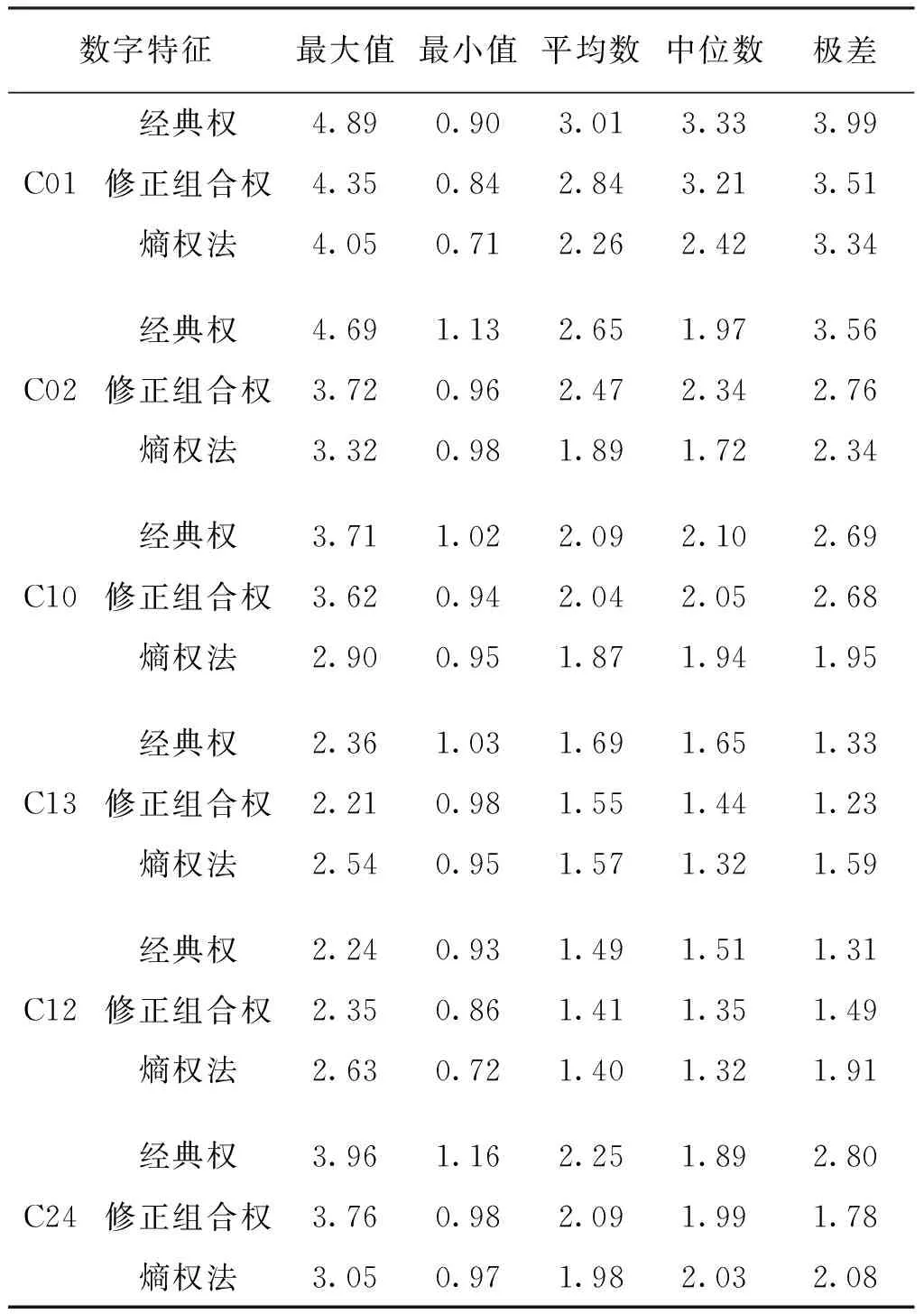
表1 组合预报模型19次短期预报精度统计表Tab.1 Combined forecast model 19 short-term forecast accuracy statistics table ns

结合图1、2，分析表1可以看出：

(1) 本节介绍的3种组合预报模型都能有效地综合各单一模型的预报结果，其中，由于修正经典权组合预报模型综合考虑了各单一模型的拟合效果和历史时段的预报效果，其预报精度在一定程度上高于经典权组合预报模型。对比RMSE平均值和RMSE极差这两项指标，可以看出，修正经典权组合预报模型预报结果平均精度较高，预报的稳定性也更好，可以更好地平衡各单一模型的预报精度。

(2) 熵权法组合模型预报结果的多数统计指标在一定程度上优于其它两种组合方法，说明该方法组合效果好，避免了经典权法有时会对拟合效果好但预报效果不一定好的单一模型分配过高权重的问题。

(3) 值得注意的是，本节的3种组合预报模型均属于线性组合的形式。从图1中可以发现，线性组合中不会出现劣组合，即组合预报模型的RMSE值不会大于各个单一预报模型预报误差的最大RMSE值;有时还会出现优组合，即组合预报模型的RMSE值小于各个单一预报模型预报误差的最小RMSE值。

在本次试验中，熵权组合模型出现优组合的次数多于其它两种组合模型。

3.2 中长期预报

中长期预报试验选用的是数据较为完整的MJD为58 594.0至58 616.0(2019-04-21～2019-05-13)共计23天的精密卫星钟差产品，钟差采样间隔为 5 min。算例中先用前288个历元(时长为24 h)的钟差数据分别用QPM和GM建模，预报未来72 h的钟差，这样一共可以进行20个时段的预报试验。而且对于建模的288个钟差数据来说，既有观测值，又有两种模型的建模拟合值，因此可以构建组合预报模型。

对选取的6颗卫星钟精密钟差的预报结果见图3。

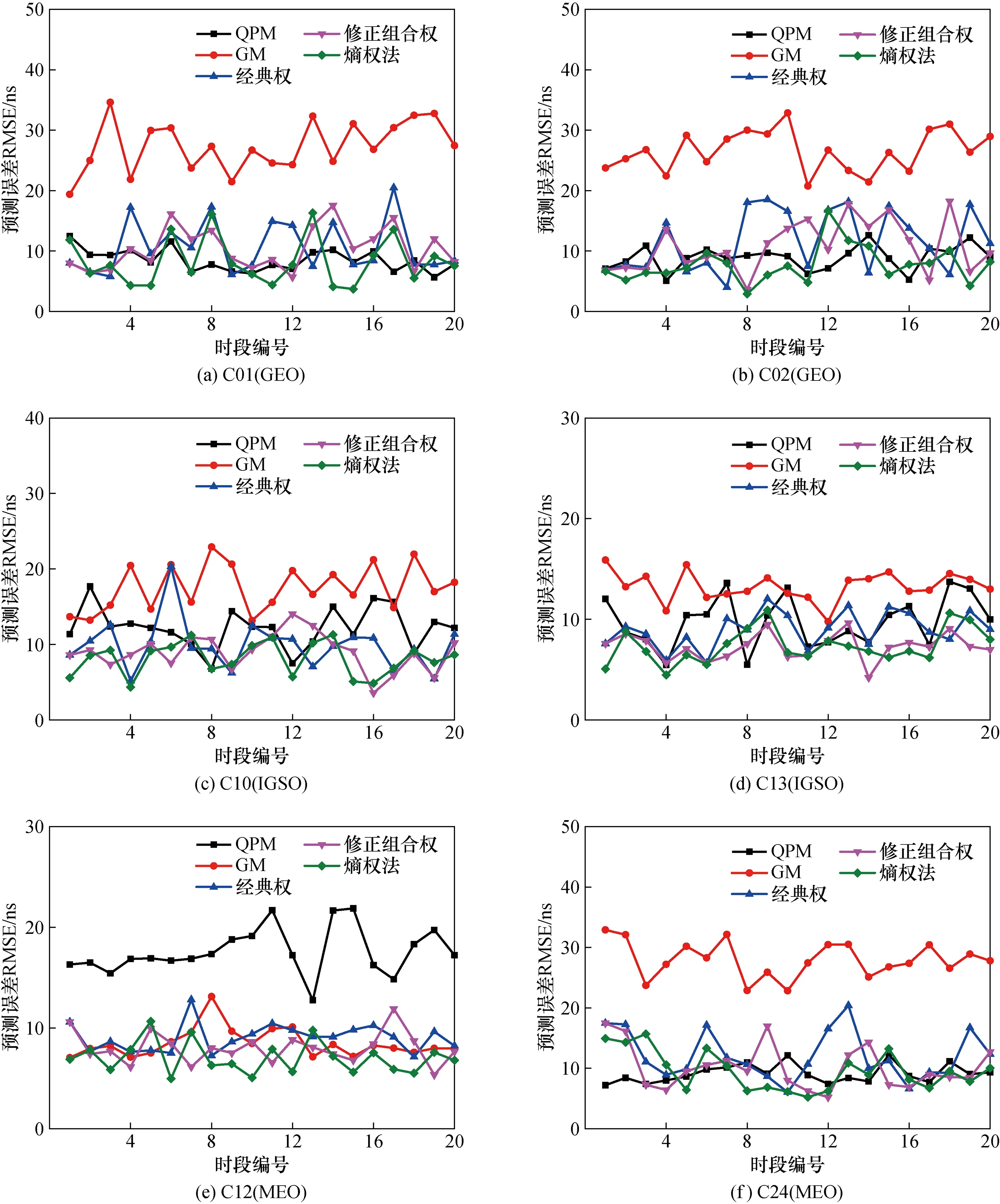
图3 各颗卫星的中长期钟差预报残差RMSE统计图Fig.3 Statistical map of medium-and long-term clock error forecast residual RMSE for each satellite

表2给出了3种组合预报模型20次钟差预报误差的RMSE序列的统计结果。

表2 组合预报模型中长期预报精度统计表Tab.2 Combined forecast model medium-and long-term forecast accuracy statistics table ns

结合图1，分析图3和表2可以看出：

(1) 随着预报时间的增加，各模型预报精度都会逐渐降低。6颗参与钟差预报试验的卫星中，有5颗卫星(C01、C02、C10、C13、C24)QPM的预报结果优于GM，这可能是因为QPM是一种体现卫星钟物理特性的模型。

(2) 对于同一组卫星钟差序列，不同预报模型的预报效果差异较大。例如对于C24(MEO)卫星，QPM预报精度最高，对于C12(MEO)卫星，QPM预报精度最差而GM预报精度相对较高。因此，应该根据卫星钟的特点，对不同的钟差序列选择合适的预报模型，而本文引入的熵权组合预报模型对6颗试验卫星钟差数据均可得到较为理想的预报结果，提高了钟差预报结果的可靠性。

(3) 比较3种组合模型中长期预报精度统计结果中的RMSE平均值指标，可以看出，对于多数卫星(C01、C02、C10、C12、C24)，熵权组合模型稍优于其他两种组合模型，而在预报稳定性方面，也具有一定优势。图3显示，在本次试验中，熵权法出现优组合的次数多于其它两种组合模型。

4 结 论

本文主要对常见的卫星钟差组合预报模型的建模特点及预报效果进行了比较分析。针对组合预报模型中权值难以确定的问题，本文引入了熵权组合预报模型，给出了基于熵权法的卫星钟差组合预报步骤。采用武汉大学IGS数据中心的精密钟差数据产品，以体现卫星钟物理特性的QPM和GM为子模型进行了预报试验，试验结果验证了该方法能够以较高的预报精度和相对稳定的性能进行北斗系统卫星钟差的预报工作，为高精度的卫星钟差预报提供了一种新的研究思路。