高中数学中的“隐形圆”问题*
周思宇 陈友明
(湖南省长沙市周南中学,410201)
隐形圆问题是高中数学常考的问题,深受命题者青睐.该类问题题干中往往没有明确给出圆的相关信息,而是将信息隐含在题目中,解题时必须深入挖掘题干中的条件,抽象出隐含的圆,进而利用圆的性质解决相关问题.试题的难度以中高档为主,注重考查学生的综合能力,常涉及平面向量、解三角形和解析几何等内容.
一、以圆的定义为背景模型
此类问题往往利用圆的定义或圆的几何性质确定隐形圆.
例1已知点A(-5,-5)在动直线mx+ny-m-3n=0上的射影点为B,若点C(5,-1),那么|BC|的最大值为______.
解动直线方程可化为m(x-1)+n(y-3)=0,故动直线恒过定点Q(1,3).

又因为|MC|=7>r,所以点C在圆M外,故|BC|的最大值为|MC|+r=12.
评注求出动点B的轨迹是解决本题的关键.题中A,Q为定点,且∠ABQ=90°,显然点B的轨迹是圆,故可利用圆的性质求解.
二、以三角形外接圆为背景模型
此类问题往往已知三角形的对边对角,结合正弦定理确定隐形圆.
例2(2014年全国高考题)已知a,b,c分别为∆ABC的三个内角A,B,C的对边,a=2,且(2+b)(sinA-sinB)=(c-b)sinC,则∆ABC面积的最大值为______.

评注利用对边对角确定三角形的外接圆是本题求解的切入口,解题的关键是确定动点A的位置,进而借助圆的几何性质使问题得解.
三、以阿波罗尼斯圆为背景模型
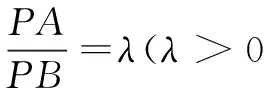
1.代数证明
以AB的中点为原点,直线AB为x轴建立平面直角坐标系,设AB=2m(m>0),则点A(-m,0),B(m,0).
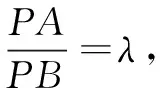
2.几何证明
先给出如下两个引理.


现利用引理1和引理2证明阿氏圆.
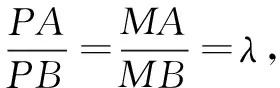

解以AB的中点O为原点、直线AB为x轴建立平面直角坐标系如图5,则点A(-1,0),B(1,0).
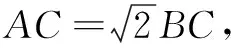

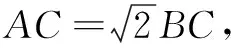
四、以距离平方圆为背景模型

1.代数证明
以AB的中点为原点、直线AB为x轴建立平面直角坐标系,设AB=2m(m>0),则点A(-m.0),B(m,0).
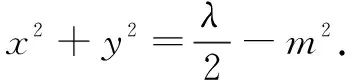
2.几何证明
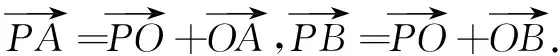
例4在平面直角坐标系xOy中,已知圆C:(x-a)2+(y-a+2)2=1,点A(0,2),若圆C上存在点M,满足MA2+MO2=10,则实数a的取值范围是______.
解设点M(x,y),由MA2+MO2=10,得x2+(y-2)2+x2+y2=10,化简得x2+(y-1)2=4,即点M在圆x2+(y-1)2=4上.
又点M在圆C上,故圆x2+(y-1)2=4与圆(x-a)2+(y-a+2)2=1相交或相切时满足题意.
评注借助数量关系MA2+MO2=10确定隐形圆,为进一步利用两圆位置关系来确定参数的取值范围提供便利条件.
五、以数量积定值圆为背景模型

1.代数证明
以AB中点为原点、直线AB为x轴建立平面直角坐标系,设AB=2m(m>0),则点A(-m,0),B(m,0).

2.几何证明






