刍议函数对称性的拓展研究
——一道高三模考题的解答与思考
胡 荣
(贵州省黔南布依族苗族自治州都匀第一中学,558000)
一、试题呈现
二、背景分析
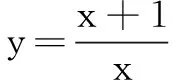
然而发展至今,此题型也有了升级版(如文首2022年贵州一模(理)第12题),函数的对称性变得隐蔽而不容易观察了,这就为我们的解题提出了新的挑战.因此,本文重点针对中心对称函数,围绕两个问题进行分析与思考:一是怎样判定中心对称函数?二是如何确定中心对称函数的对称点?
针对中心对称函数,已提出的相关结论有[1][2]:
(1)若函数y=f(x)是奇函数,则函数y=f(x-m)+n的图象关于点(m,n)成中心对称
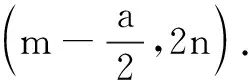
(3)对于不同的函数f(x)与g(x),若其对称中心分别为(m,n)和(m,q),则其和函数h(x)=f(x)+g(x)的对称中心为点(m,n+q).
本文在这些结论的基础上,以文首试题为出发点,进一步探究对称函数的新结论.
三、试题解答
分析通过构造两个具有相同对称中心的函数,将所有交点坐标之和利用对称中心的坐标来表达.注意函数f(x)在对称中心点处无定义,则f(x)与g(x)有偶数个交点.
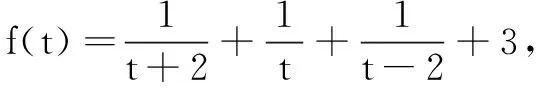
评注本题呈现的两个函数都是不能直接观察出中心对称性的,对构造中心对称函数有较高要求.此题虽能让学生意识到要利用函数对称性解决问题,但受阻于不能判定对称性,不能确定对称中心,导致学生陷入盲目,无从下手.通过对此题的分析与思考,本文对中心对称函数进行了如下推广,力图帮助学生在遇到此类问题时能把握核心与关键,能有的放矢地解决问题.
三、问题探究与思考

定理1若函数y=f(x)的对称中心为点(m,n),则函数g(x)=f(x-a)+f(x)+f(x+a)的对称中心为点(m,3n).
证明因为g(x)=f(x-a)+f(x)+f(x+a),所以g(2m-x)=f(2m-x+a)+f(2m-x)+f(2m-x-a).
又由y=f(x)的对称中心为点(m,n),得f(x-a)+f(2m-x+a)=2n,f(x)+f(2m-x)=2n,f(x+a)+f(2m-x-a)=2n.
所以g(x)+g(2m-x)=6n,即函数g(x)是以点(m,3n)为中心的对称函数.
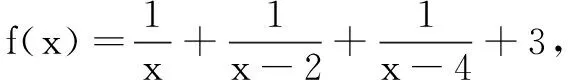
在定理1基础上进一步延伸,我们可得到如下定理.
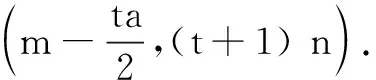
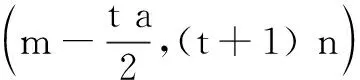
类似地,对于轴对称函数的图象,容易得到如下结论.
定理3若函数y=f(x)的对称轴为x=m,则函数g(x)=f(x-a)+f(x)+f(x+a)也以x=m为对称轴.

四、变式应用


又因为g(x)=-(x+3)3+5,故g(x)同样是以点(-3,5)为中心的对称函数.
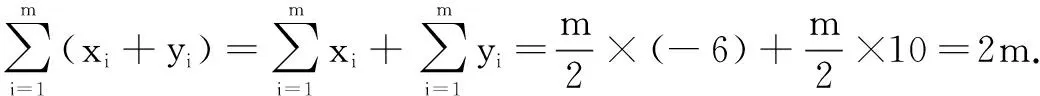

变式2已知函数f(x)=ln|x3-3x2+2x|与g(x)=|x-1|+3的图象有4个交点,则交点的横坐标之和x1+x2+x3+x4=______.
解由f(x)=ln|x3-3x2+2x|,可得f(x)=ln|x|+ln|x-1|+ln|x-2|.由定理4可得f(x)是以x=1为对称轴的对称函数.又因为g(x)=|x-1|+3同样是以x=1为对称轴的对称函数.注意到函数f(x),g(x)在x=1处的函数值不相等,则题设中的4个交点两两关于x=1对称,所以x1+x2+x3+x4=2×2=4.

