非线性兰姆波在厚度缓慢变化和衰减下的特性分析*
左炜翌 安志武† 张碧星
(1 中国科学院声学研究所声场声信息国家重点实验室北京 100190)
(2 中国科学院大学北京 100190)
0 引言
板壳结构广泛用于机械、民用和航空航天等领域。这些结构在时变载荷下由于疲劳产生的微裂纹会降低材料性能,进而引发断裂。因此,在材料早期疲劳时检测微裂纹对于避免工程部件和结构的灾难性故障非常重要。非线性兰姆波可以长距离传输并检测整个板壳结构的内部缺陷,因此在超声无损检测和结构健康监测领域得到了广泛的应用[1-4]。
一些理论研究讨论了兰姆波二次谐波的产生机制和效率。de Lima等[5]和Deng等[6-7]使用二阶微扰近似和模态分析方法研究了兰姆波二次谐波生成的复杂问题。由于兰姆波各个模式具有色散特性,在基频波和二次谐波的波数不匹配时会产生拍频效应,二次谐波难以随传播距离增加而累积。S0模态在低频范围内的色散非常微弱,相比其他模态容易产生累积非线性效应。Zuo等[8]和Wan等[9]分析了由S0模态产生的非线性兰姆波,测量了一段传播距离范围内线性增加的S0模式的二次谐波。在某些场景下,变厚度板壳更接近实际工程结构。Hu等[10]基于对称兰姆波模式分析了缓慢线性变厚板中非线性导波的理论模型的微扰法近似解,并通过仿真模拟和实验对其进行了验证。然而,在测量长距离结构或黏弹性材料时,导波的衰减会影响二次谐波的激发和接收[11-12],导致模型失效。Kanda等[13]用多尺度法得到了均匀厚度板下的二次谐波衰减规律,但由于求解方程时将复波数近似成实数,使得在衰减较大的情况下结果不准确。
为此,本文基于Hu等[10]的工作,完善了兰姆波二次谐波在变厚度板中传播的理论推导过程,使该理论适用于角度变化更大的变厚度板,并将理论的适用范围推广至黏弹性介质。通过半解析计算给出了S0模式在厚度保持均匀、线性增加、线性减小、曲线变化下的二次谐波的累积和传播规律,并利用有限元方法对该理论的适用范围进行了分析。
1 复数域的兰姆波频散曲线
兰姆波是在固体板中传播的超声导波。由于波导界面存在自由边界条件,纵波和横波在上下边界处相互转换,产生叠加和干涉,于是产生了一种与固体波导几何形状有关的超声导波模式。因此兰姆波具有多模式和色散特性。当考虑声波衰减时,兰姆波的频散曲线对应的波数和相速度均是复数。本文以应用广泛的有机玻璃(PMMA)作为算例,表1列出了PMMA材料的参数,包括密度、纵波和横波的声速、对应的衰减系数[14]和三阶弹性常数[15]。
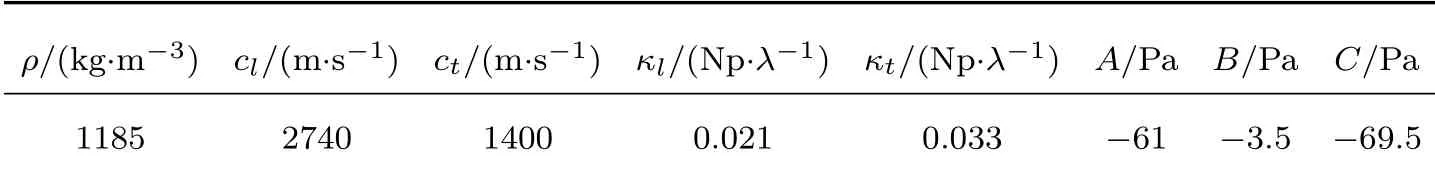
表1 PMMA的各项参数Table 1 Parameters of PMMA
PMMA是一种黏弹性材料,声波在其中具有较大的衰减。基于Kelvin-Voight模型,其纵波速度和横波速度都是复数:
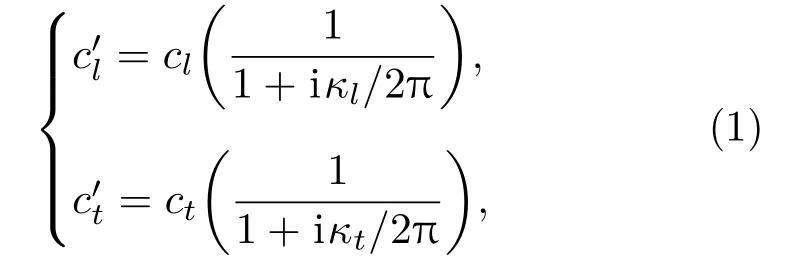
其虚部项表示声波的衰减。如图1所示,将复速度带入兰姆波的频散方程可以得到各个兰姆波模式的频散曲线。由于考虑了声波的衰减,在给定频厚积下,兰姆波的任何模式都有负的速度虚部,因此传播模式和非传播模式不再有明显的区分。
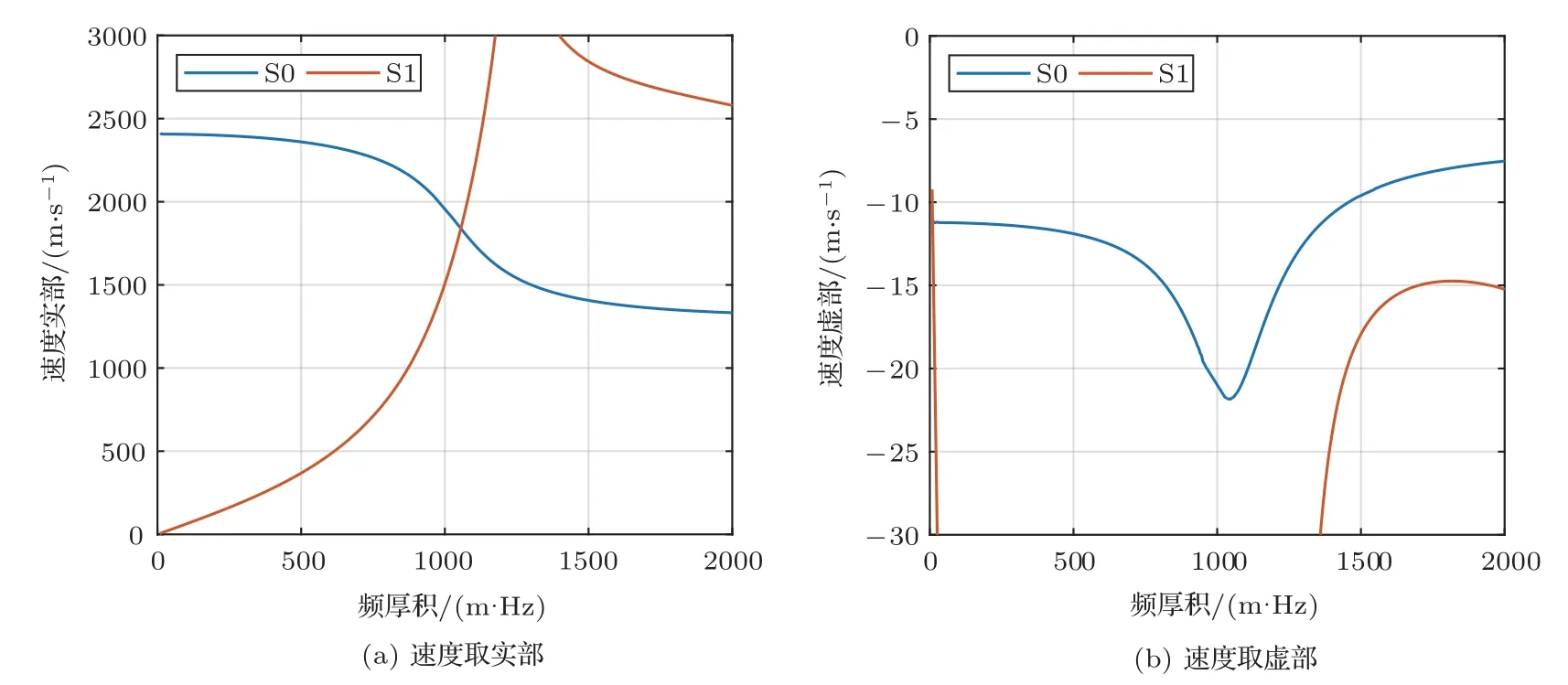
图1 兰姆波对称模式在复数域的频散曲线Fig.1 Dispersion curve of Lamb wave symmetric modes in complex domain
2 等厚度板中的兰姆波二次谐波解析解
非线性声波方程缺乏一般的研究方法,但在弱非线性效应的情况下微扰法可以取得很好的近似。微扰法的基本思想是把待求的物理量表示成收敛的级数。该级数中的主要项是完全可解问题的解,而高阶项描述完全可解问题相比实际问题产生的偏差。参照图2中的坐标,基于微扰法的思想,将兰姆波的位移写为基频项和二阶微扰项的和:

图2 等厚度的平板Fig.2 The uniform-thickness plate

其中,需要满足|u(2)|≪|u(1)|。兰姆波基频的位移可以展开为各个模态的位移:

其中,A(1)n为第n个模式的振幅,¯u(1)n(y)为单位振幅下的位移场。在实际测量时,如果测量得到了兰姆波模式n的表面振动位移uy(h),则该模式的振幅为An=uy(h)/¯uy(h)。
考虑三阶弹性常数时,兰姆波基频项将产生体积力fi和表面应力σij:

其中,δij表示克罗内克函数,下标表示爱因斯坦求和约定,上标(1,1)表示体积力和表面应力是基频波位移的二次型,因此频率是基频波频率的两倍。将体积力作为外力,得到二倍频的有源声波方程:

同时在上下边界y=±h处满足自由边界条件:
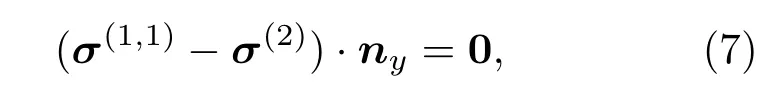
其中,σ(2)是二次谐波在仅考虑二阶弹性系数(线性情况下)产生的应力张量,ny是沿y轴方向的单位向量。将二倍频的兰姆波位移u(2)同样展开为各个模式的和:

出于计算方便起见,二次谐波第n个模式的振幅包含了随传播距离x变化的相位项。
在超声无损检测的实际应用中,由于高频兰姆波的激发和接收较为困难,通常使用低频S0模式作为激发非线性兰姆波的基频波,并同样接收二倍频的S0模式作为检测信号[8-10]。从图1的频散曲线可以看出,在频厚积较小的部分,S0模式只有轻微的色散。而其他模式和S0模式相速度严重不匹配,所以难以产生累积的二次谐波。因此本文接下来也限定为S0模的基频波和二次谐波。将位移公式(8)带入有源声波方程(6)和边界条件(7)得到:

3 缓慢变厚度板的二次谐波方程
如图3所示,当板的厚度沿传播距离发生变化时,对应了图1中兰姆波频厚积的变化,但是当厚度变化足够缓慢时,发生模式转换和反射的振幅可以忽略不计,同时近似认为依然满足水平自由边界条件。然而,式(9)中的相关物理量均会随传播距离x发生变化。因此式(9)需要改写为

图3 厚度缓慢变化的板Fig.3 The plate with slowly-varying thickness
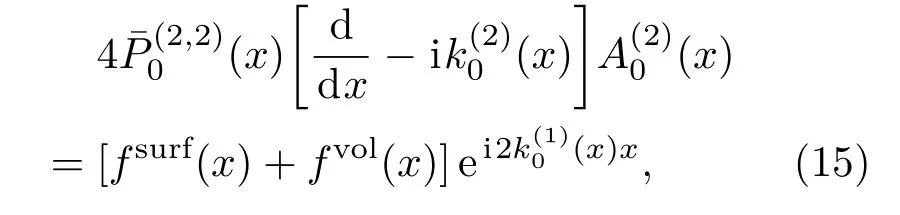
其中:
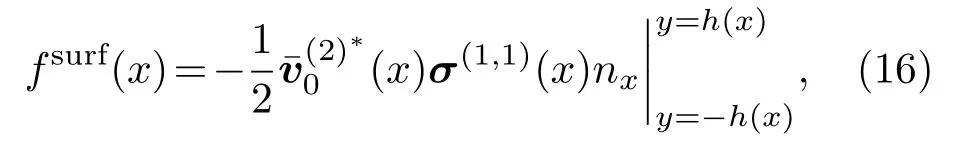
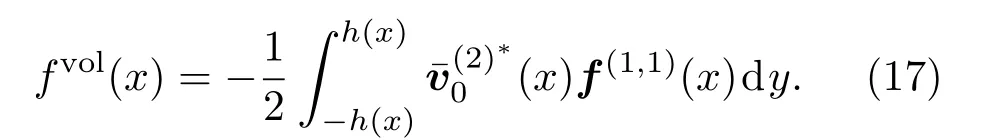
该方程具有解:
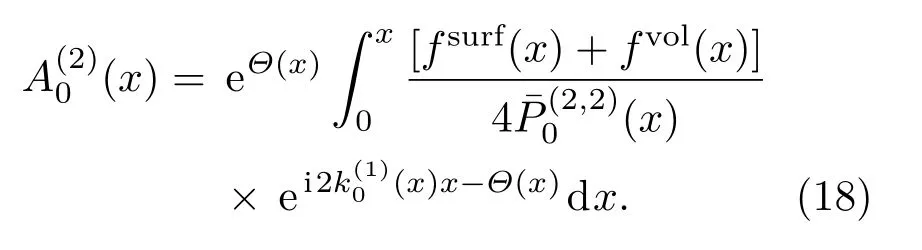
其中包含二次谐波相位的累积项:

由于厚度变化d(x)的任意性,实际计算时需要借助图1中的频散曲线进行数值积分求解。
Hu等[10]运用了类似的方法,在角度为0.17°时完成了厚度线性变化板的实验验证工作。本文改进了Hu等[10]的推导过程,使理论适用于角度更大的变厚度板,并将理论的适用范围推广至黏弹性介质。
4 算例和理论成立条件
本文在4种不同几何形状的板中设置90 kHz的S0模式兰姆波,使用式(18)进行数值积分求解,并运用有限元方法(Finite element method,FEM)进行仿真验证。有限元仿真使用显性动力学程序,使用高斯调制的20个周期正弦波作为激励信号。计算结果如图4所示。
在图4(a)中,由于色散特性,兰姆波二次谐波的传播产生了拍频效应,色散长度符合式(9)。不考虑声波衰减时,二次谐波的振幅经过色散长度的整数倍后会归零。当考虑声波衰减或板的厚度缓慢变化的情况时,拍频效应将不再严格地被满足。二次谐波的振幅依然会沿着传播距离而振荡,但在基频能量消失前不会归零。如图4(b)~图4(d)所示,基于不同几何形状的板,二次谐波的振幅累积具有不同的特性。
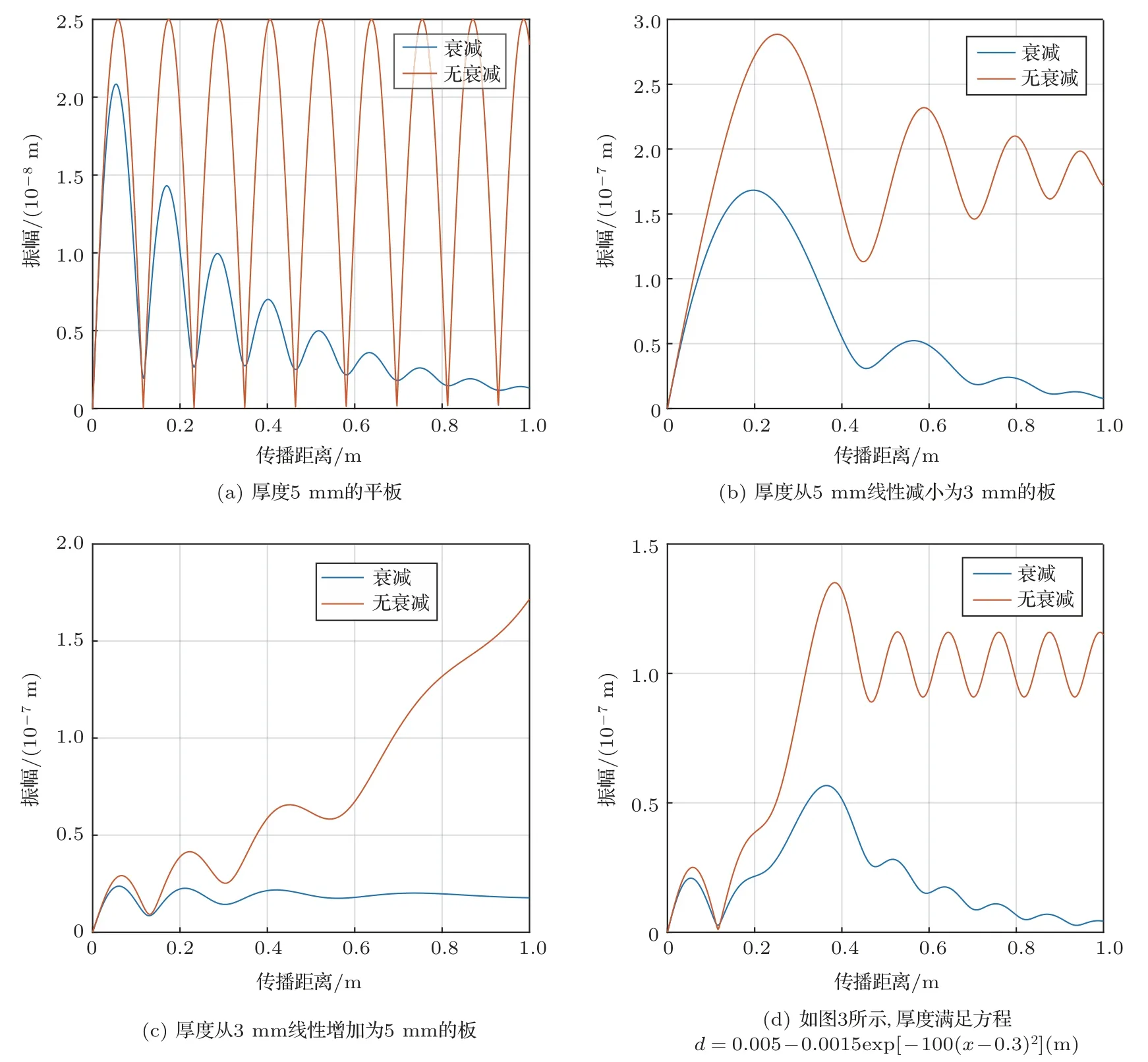
图4 4种长度为1 m的板中的二次谐波振幅Fig.4 Second harmonic amplitudes in four plates with length of one meter
该半解析方法与有限元仿真结果吻合度较高,据此,基于有限元仿真的结果可以讨论该理论成立的条件。通过前文的分析可以得出该理论经过了3处近似:
(1)微扰近似。微扰近似要求振幅不能过大,累计非线性谐波相比起基频波是一个小量。一些实验中典型的二次谐波振幅会小2~3个数量级。
(2)无散射近似。Feng等[16]提出了一种半解析计算方法,可用于计算时间上无限长的兰姆波在变截面的板中的散射情况。另外也可以基于有限元仿真结果判断基频波的能流大小。对于坡度变化最大的图4(d)模型,其最大角度为5.5°,有限元计算结果表明基频波的能流在通过高斯变化的窄边后损失小于1%,可以近似认为在传播过程中无散射发生。
(3)小角度近似。当厚度变化的角度过大时,式(7)表示的上下水平自由边界条件不再得到满足。
通过第4节的4个算例发现,在坡度小于5°,同时最大厚度不超过最小厚度两倍的情况下,可以很好地满足上述的近似条件,使得该理论方法与有限元仿真的结果一致。
5 结论
本文运用微扰法推导了考虑声波衰减时在厚度缓慢变化板中兰姆波二次谐波的波动方程,并通过半解析方法给出了S0模式二次谐波的累积和传播规律。用有限元仿真验证了理论,并分析了理论成立的条件。结果表明,在满足微扰近似、无散射近似、小角度近似的情况下,本文的理论模型具有较高的精度。因此,非线性兰姆波检测技术有望应用于波导厚度缓慢变化和存在衰减的情况。

