迭代收缩非线性状态约束滤波算法

贺 姗，刘沫萌,2,3，李 迎

(1.西安工程大学 计算机科学学院，陕西 西安 710048；2.陕西省服装设计智能化重点实验室，陕西 西安 710048；3.新型网络智能信息服务国家地方联合工程研究中心，陕西 西安 710048)

0 引 言

在状态估计问题中，系统的状态向量可能会受到许多约束条件的限制，如果可以用这些约束条件对状态向量进行修正，便可以更加逼近系统真实值，从而使得滤波估计结果更加精确。因此，研究约束条件下滤波算法是非常有意义的[1-3]。

约束条件分为线性以及非线性。解决线性约束问题的相关方法可以参见Simon的综述文章[1]。针对非线性约束下的状态估计问题，人们也进行了很多研究并提出了很多算法。1995年，Michalska等人提出了水平滑动估计算法(Moving Horizon Estimation，MHE)[4]，该算法在非线性约束条件的限制下，采用最优化方法对一个区间内的估计误差和观测误差进行最小化，能够获得很高的滤波精度，但其算法时间复杂度较大，即使实现过程中使用了较小的滑动窗口，仍然需要花费很多的时间。1997年，De Geeter等人给出了平滑约束卡尔曼滤波(Smoothly Constrained Kalman Filter，SCKF)[5]，该算法滤波精度较高，时间复杂度较低。2002年，Simon等人提出的一阶泰勒级数展开非线性约束算法(Linearized Constrained，LC)[6]，该算法采用一阶泰勒级数展开方法对非线性状态约束函数进行线性化，再通过线性化约束算法中的投影方法进行滤波。为了提高滤波精度，2009年，Yang等人提出了一种新的滤波算法─二阶泰勒级数展开非线性约束方法(2ord Nonlinear Constrained，2ord NC)[7]，其滤波精确度高于LC算法，但其耗费时间较大。除了MHE算法之外，其余几种算法也都只能在弱非线性约束中适用，且都需要计算非线性状态约束函数的雅克比矩阵。

针对以上问题，文献[8]中提出了一种基于UT变换的迭代收缩非线性状态约束滤波算法(为了与下文保持一致，此处简称为ISNC-UKF)，该算法可以处理强非线性约束下的状态估计问题，能够获得较好的滤波精度，时间复杂较小，且实现过程中无需计算非线性状态约束函数的雅克比矩阵。在该算法的启发下，将文献[8]中的算法进行一般化，该文提出了一种解决非线性状态约束的算法框架。该方法可以采用多种基于确定点采样滤波算法。包括：不敏卡尔曼滤波算法(Unscented Kalman Filter，UKF)[9]、求积分卡尔曼滤波算法(Quadrature Kalman Filter，QKF)[10]、中心差分卡尔曼滤波算法(Central Divided Differences Kalman Filter，CDKF)[11]、容积卡尔曼滤波算法(Cubature Kalman Filter，CKF)[12]。结合上述四种非线性滤波算法，提出了高斯分布下的一般性非线性状态约束方法的框架。为了减小基点误差[7]对于滤波结果的影响，采用迭代的方法，使得约束逐渐变强，最终获得更好的滤波精度。从而得到了几种相应的解决非线性状态约束的滤波算法，即：迭代收缩非线性状态约束求积分卡尔曼滤波算法(Iterative Shrinking Nonlinear State Constraints Based on Quadrature Kalman Filter，ISNC-QKF)、迭代收缩非线性状态约束中心差分卡尔曼滤波算法(Iterative Shrinking Nonlinear State Constraints Based on Central Divided Differences Kalman Filter，ISNC-CDKF)、迭代收缩非线性状态约束容积卡尔曼滤波算法(Iterative Shrinking Nonlinear State Constraints Based on Cubature Kalman Filter，ISNC-CKF)。这些算法在保证较高滤波精度和较低时间复杂度的前提下，能够解决非线性约束函数雅克比矩阵不存在或者雅克比矩阵难以求解的问题。

1 问题描述

假定高斯条件下系统的状态方程和量测方程分别为：

xk=f(xk-1)+vk

(1)

yk=h(xk)+nk

(2)

其中，xk和yk分别是k时刻的状态值和量测值，f和h分别为状态转移函数和量测函数，vk～N(0,Qk)和nk～N(0,Rk)分别为过程噪声和量测噪声，且它们互不相关。现假设状态值xk受到的非线性约束函数如下：

g(xk)=dk

(3)

式中，g与dk分别为已知的非线性状态约束函数和向量。此约束问题即为通过式(3)对状态向量进行修正从而得到更加精确的状态估计值。

2 高斯非线性约束滤波的贝叶斯形式

在式(3)中，x为服从高斯分布的随机向量，因此函数g(x)的值也可以写成一个积分形式：

(4)

其中，D为积分区域，g(.)为任意非线性函数，w(.)为一个加权函数。式的积分为“非线性函数×高斯密度”形式，因此可以采用数值解法进行近似[13-14]，即：

(5)

上述数值积分问题的关键点在于：确定西格玛点以及相应权值。假设对于n维的状态向量，可以分别借助UKF、QKF、CDKF、CKF算法中的思路进行求取。其中借助UKF算法的实现思路已经在文献[8]中予以介绍，因此该文予以省略。

QKF滤波是在高斯厄米特滤波基础上提出的，下面给出高斯厄米特求积分规则[10]。假定一个随机变量x，其高斯密度为N(x;0,1)，则可得函数g(x)的期望值为：

(6)

(7)

(8)

其中，(vi)1表示J的第i个特征向量的第一个元素。因为随机变量x中各个元素互不相关，可将式扩展至多维形式：

(9)

CDKF是借助Stirling插值多项式近似非线性函数，采用中心差分代替泰勒级数展开中的一阶和二阶导数，实现非线性函数向线性函数的转换[11]。即有：

(10)

(11)

其中，h表示中心差分区间长度，对于高斯假设下的系统，h取值为3，δx表示一个具有零均值且与随机变量x有着相同协方差的随机变量。

CDKF的具体实现方法和UKF的类似，都是采用了对称策略求取Sigma点χi，对于n维的随机变量x需计算2n+1个Sigma点χi。

(12)

(13)

(14)

其相应权值为：

w0=(h2-n)/h2

(15)

wi=1/2h2,i=1,2,…,2n

(16)

CKF确定点以及相应权值的计算根据容积规则[12]。考虑下面一个求积分问题:

(17)

为了数值化计算上式积分问题，首先将其转换为一个更常用的球面径向形式，需将x转换成球面半径r和方向向量y的乘积，即：x=ry，其中，yTy=1,那么上式可写为：

(18)

其中，Un表示半径为1的球表面，δ(·)为积分域Un内的元素。令:

(19)

则式(18)可写为：

(20)

针对式(19)和式(20)，分别采用mr点高斯厄米特求积分规则和ms点球面规则，可得到mr×ms点的球面径向求容积规则为：

(21)

(22)

(23)

那么，对于式(17)、式(4)中的积分问题就可以通过上述方法解决。

(24)

当mr=1，ms=2n时，对于一个三阶球面径向规则，需计算出m=2n个容积点εi，计算公式为：

(25)

其相应权值为：

wi=1/m,i=1,2,…,m

(26)

3 迭代收缩非线性状态约束滤波

为了解决非线性状态约束问题，在状态向量符合高斯分布的假设下，采用上述方法对积分进行数值近似。为了进一步提高状态估计的精度，给非线性约束施加一系列由强到弱的噪声，通过最佳量测[15-16]的方法迭代求取状态估计值。下面分别对这四种方法具体实现过程进行阐述。

ζi,k=g(εi,k),i=0,1,…,2n

(27)

计算非线性变换后的均值和协方差：

(28)

(29)

(30)

为了减小基点误差对于状态向量估计的影响，给非线性状态约束函数施加一系列噪声Rd,k。首先用a×Pζζ,k将其乘积值作为第一次迭代时Rd,k的值，其中a∈[0.01,0.1]为一个常数，在实现过程中通常取经验值，文中的取值为0.01。在之后的迭代中，Rd,k=Rd,kexp(-i)，i为迭代的次数，使得方差逐渐递减，由最小方差估计准则得到具有非线性状态约束条件下的均值和协方差，即：

Pζζ,k=Pζζ,k+Rd,k

(31)

(32)

(33)

ISNC-UKF方法的具体实现过程已经在文献[8]中详细介绍，不再赘述。其他几种方法的实现过程与ISNC-CKF类似，下面直接给出这些方法的实现步骤。

ISNC-QKF方法的实现步骤如下：

Step2：用式(27)～式(30)计算非线性变换后的均值及其协方差；

Step3：第一次迭代时，令Rd,k=aPζζ,k，在之后的迭代中Rd,k=Rd,kexp(-i)，i为迭代的次数；

Step4：采用式(31)获得当前的方差值Pζζ,k；

Step5：采用式(32)和式(33)获得系统的状态估计值以及方差；

ISNC-CDKF方法的实现步骤如下：

Step2：用式(27)～式(30)计算非线性变换后的均值及其协方差；

Step3：第一次迭代时，令Rd,k=aPζζ,k，在之后的迭代中Rd,k=Rd,kexp(-i)，i为迭代的次数；

Step4：采用式(31)获得当前的方差值Pζζ,k；

Step5：采用式(32)和式(33)获得系统的状态估计值以及方差；

在上述迭代收缩非线性状态约束滤波方法实现过程中，迭代次数为3～5次时就能够得到一个较小且较为稳定的估计均方根误差值，迭代更多次并不能对滤波结果有明显改善，这是因为经过多次迭代后Rd,k=Rd,kexp(-i)使得方差逐渐递减，对于方差Pζζ,k的影响就会很越来越小，从而也减弱了对于估计均方根误差收敛的影响。

4 仿真实验及结果分析

利用钟摆运动[1]仿真实例验证滤波算法。可设系统的动态方程及量测方程为：

θk+1=θk+Tωk+vθ,k

(34)

(35)

yk=[θkωk]T+nk

(36)

其中，已知k时刻的系统状态向量为xk=[θkωk]T，θk则为k时刻钟摆所摆动的角度值，ωk为k时刻钟摆动的角速度值。yk为k时刻系统量测值，T表示步长，g表示重力加速度，L表示钟摆长度，且[vθ,kvω,k]T～N(0,Qk)和nk～N(0,Rk)分别为互不相关的过程噪声及量测噪声。

由机械能守恒定理可知，钟摆运动系统中的状态向量应符合如下的非线性状态约束条件：

(37)

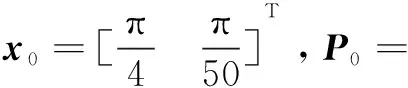
状态估计过程采用扩展卡尔曼滤波算法(Extended Kalman Filter，EKF)[17]，再通过非线性约束函数即式(37)、式(3)对状态估计结果进一步进行修正，采用以下滤波算法：水平滑动估计滤波算法(MHE)、平滑约束卡尔曼滤波算法(SCKF)、一阶泰勒级数展开非线性约束算法(LC)、二阶泰勒级数展开非线性约束滤波算法(2ordNC)、最佳量测滤波算法(PM)、迭代收缩非线性状态约束不敏卡尔曼滤波算法(ISNC-UKF)以及文中给出的迭代收缩非线性状态约束求积分卡尔曼滤波算法(ISNC-QKF)、迭代收缩非线性状态约束中心差分卡尔曼滤波算法(ISNC-CDKF)及迭代收缩非线性状态约束容积卡尔曼滤波算法(ISNC-CKF)进行实验仿真。

表1为各种约束滤波算法的误差值，包括角度误差值以及角速度误差值，将算法误差性能由高到低排序为：MHE4、MHE2、SCKF、ISNC-CDKF、ISNC-QKF、ISNC-CKF、ISNC-UKF、2ordNC、LC、PM及未施加非线性约束函数的EKF。从表中可以看出，文中给出的滤波算法ISNC-CDKF、ISNC-QKF、ISNC-CKF的误差差别很小，和已有的滤波算法ISNC-UKF类似，且和滤波算法SCKF的误差基本相当。

表1 各种算法误差性能对比

表2给出了上述滤波算法实现过程中所耗费的时间，算法耗费时间从高到低依次是MHE4、MHE2、ISNC-QKF、ISNC-UKF、ISNC-CDKF、ISNC-CKF、2ordNC、SCKF、PM、LC以及没有加非线性约束状态条件的EKF。从表中的数据可以看出，该文提出的滤波算法中ISNC-CDKF 及ISNC-CKF其耗费时间基本相当，和ISNC-UKF算法耗费时间类似，而ISNC-QKF的耗费时间也应该和上述三种滤波算法相当，但是由于在算法实现过程中计算积分点时耗费了额外的时间，而积分点的计算可以离线获得，故ISNC-QKF和ISNC-CKF、ISNC-CDKF及ISNC-UKF的耗费时间是基本相当的。虽然SCKF滤波算法和该文提出的三种滤波算法相比较，误差较低、耗费时间少，但该算法值仅适用于弱非线性情况，对于非线性约束函数雅克比矩阵不存在或者雅克比矩阵难以求解的情况，若使用该算法，只会使得滤波失效，而该文给出的这三种算法可以适用于强非线性情况，能够避免上述问题。MHE滤波算法和这三种算法相比较，虽然误差很低，但是其耗费时间却很大。综上所述，给出的三种算法不仅无需求解非线性约束函数雅克矩阵，且能够使得滤波结果更加逼近真实值，算法处理时长也较短。

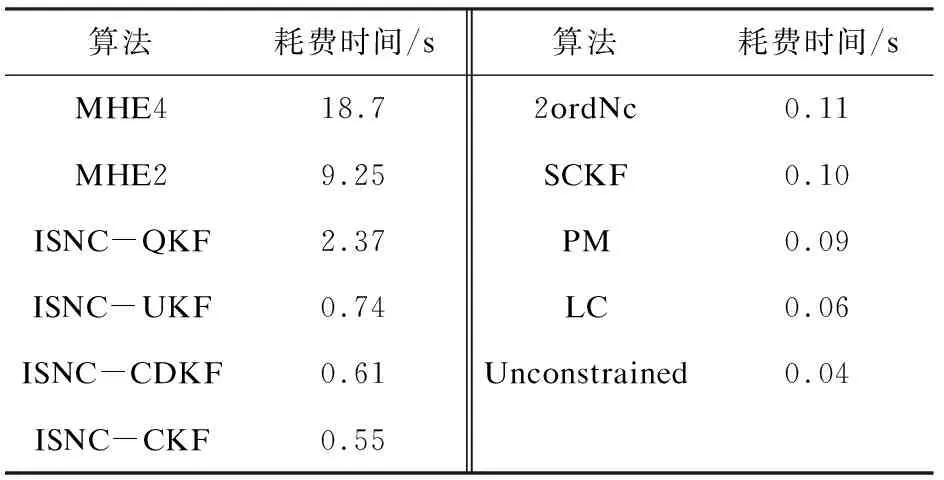
表2 各种算法消耗时间对比

5 结束语

在处理非线性状态约束估计问题时，若约束函数为弱非线性时，可采用泰勒级数展开方式近线性化非线性约束函数，但是在实现过程中可能会出现以下问题：状态估计中需求解非线性函数的雅克比矩阵，然而雅克比矩阵也可能不存在或易于求解，另外在许多应用条件的影响下，滤波结果也可能会出现精度差、估计有偏或者发散等问题。为了避免上述问题，提出了高斯假设下的一类迭代收缩非线性状态约束滤波方法，并给出了几种实现算法，包括：ISNC-QKF、ISNC-CDKF、ISNC-CKF。与已有的ISNC-UKF算法性能类似，都无需求解非线性函数的雅克比矩阵，算法实现过程中采用最佳量测的方法迭代求解状态估计值，滤波精度较好，时间复杂度适中。