基于层次观测认知诊断的考生成绩预测方法

方寒月，曹浪财

(厦门大学航空航天学院，厦门市大数据智能分析与决策重点实验室，福建厦门361005)

认知诊断是智慧教育中的一个基本问题，旨在发现考生对特定知识点的掌握程度[1-2]，图1展示了一个认知诊断的示例.通常，考生完成试题(e.g.,e1,e2,e3)并留下他们的回答(e.g., 对或错).接着，我们的目标是依据该答题记录推断出考生对试题中知识点的实际掌握程度.这些诊断报告可以用于预测考生的试题得分，为后续的个性化补救和教学计划改进提供帮助.目前关于认知诊断的研究主要集中在试题所考察的多个知识点之间的相互作用上[3-4].同时，越来越多的研究人员正在将神经网络应用于认知诊断工作中[5-6]，且已证实效果远优于传统认知诊断方法.其具体做法是使用神经网络代替传统认知诊断模型中的函数关系.

现有的认知诊断工作主要存在以下两个问题：1) 客观题和主观题的差异尚未得到充分研究[7-8].客观题以完全正确或完全错误的方式评分，而主观题的评分却可以是部分正确的.显然，考生在回答主观题时，很难通过猜测答案而得到正确的回答，或者因为粗心而得到错误回答，主观题可以更好地衡量考生对试题的实际掌握程度.因此，同时处理客观题和主观题中的信息是非常有必要的，而不是将主观题视为客观题来处理[9].2) 现有基于深度学习的认知诊断模型虽然准确性较高，但是不能清晰地诊断出不同考生对同一知识点的掌握程度差异，可解释性相对不足[5-6].此类模型以神经网络的嵌入层表示考生和试题，并使用考生和试题嵌入向量的差值作为网络的输入，实现对考生的诊断.为了充分地利用考生和试题嵌入向量的信息，模型通常选择sigmoid或tanh作为激活函数.但是随着网络层数的加深，使用上述激活函数会导致梯度消失的问题[10-11]，使得模型无法清晰学习出考生的嵌入向量表示，不能有效诊断出不同考生对同一知识点的掌握程度.

图1 认知诊断示例Fig.1The example of cognitive diagnosis

针对上述问题，考虑到主观题和客观题观测到的得分类型是不同的，以及梯度消失造成的考生嵌入向量的不充分学习，本文首先提出了一种基于层次观测的认知诊断框架(hierarchical observational-based cognitive diagnosis framework,HoCDF).HoCDF是一个以三层框架(知识点掌握程度、试题掌握程度、试题观测分数)来模拟生成试题预测分数的逐级过程.然后采用了受神经网络启发的解决方案来处理这个三层框架中的层次关系，围绕主观题和客观题信息的差异，从观测角度实现对不同试题类型的联合建模；接着，HoCDF通过增加不含激活函数的单层网络作为额外通路，缓解了模型的梯度消失，提高了对考生嵌入向量的学习效果，更加充分地诊断出不同考生对同一知识点的掌握程度，从而提高模型的可解释性及性能表现；最后，对考生成绩的预测验证了HoCDF的有效性.

1 模型基础

1.1 符号定义

本研究中假设在学习系统中有N个考生、M个试题和H个知识点，可以表示为S={s1,s2,…，sN}，E={e1,e2,…，eM}和K={k1,k2,…，kH}.其中，小写字符表示任一个元素，大写字符表示元素的总数(e.g.,n表示第n个考生，N表示考生总数).HoCDF定义了一些具体的符号用来支撑整个框架的实现.

θnh表示考生sn对知识点kh的掌握程度,cmh表示试题em中知识点kh的难度水平,ρnm表示考生sn对试题em的掌握程度,Rnm表示考生sn在试题em上的观测分数.

此外使用矩阵Q=(Qmh)M×H表示试题em与知识点kh的关系.其中Qmh=1表示试题em与知识点kh有关，Qmh=0表示试题em与知识点kh无关(通常由教育专家标记).HoCDF借助考生的分数和Q矩阵，挖掘考生对知识点的掌握程度.

1.2 模型假设

假设1考生在主观题和客观题上的得分，是对试题掌握程度的不同观测结果，与客观题相比，考生对主观题的得分应更接近于考生对试题的实际掌握程度.

通常，考生对试题的掌握程度越高，考生在试题上的得分就越高.但是由于客观题和主观题的评分方式不同，相同的试题的掌握程度，考生在主客观题中却可能获得不同的分数.如图2所示，同一道试题分别设计成客观题和主观题，理论上考生对这两道试题应当有同样的掌握程度.实际情况是：客观题的分数是一个二分类的结果(完全正确或者完全错误)，而主观题却可以是正确的、错误的或者部分正确的.因此考生在对试题的掌握程度相同的情况下，主观题可以更好地衡量考生对试题的实际掌握程度. (e.g., 当考生答案为30(m)，在客观题中考生往往获得0分.而在主观题中，由于成功列出表达式，将得到部分分数).

图2 客观题和主观题的示例Fig.2An example of objective and subjective problems

假设2增加不含激活函数的单层网络作为额外通路，可以缓解梯度消失造成的考生嵌入向量的不充分学习.

现有基于深度学习的认知诊断模型通常使用考生和试题嵌入向量的差值作为网络输入，为了保证对输入的正负进行激活，以及对称性，模型通常选择了sigmoid作为激活函数，但是随着网络层数的加深，上述激活函数将会导致梯度消失的问题[10-11]，使得考生的嵌入向量不能得到充分学习.为此，本文在现有的认知诊断网络模型的基础上，增加了不含激活函数的单层网络作为额外通路.由于该单层网络不含激活函数，并且直接连通嵌入层和输出层，避免了由于激活函数导致的梯度消失，因此增加不含激活函数的单层网络作为额外通路，可以提高对考生嵌入向量的学习效果，可以更加充分地诊断出不同考生对同一知识点的掌握程度差异.

2 层次观测认知诊断

2.1 HoCDF

基于上述两个假设，构建的HoCDF如图3所示，整个框架关联了考生因素(知识点掌握程度)、试题因素(知识点难度、试题掌握程度、试题观测分数构成)以及交互函数(神经网络)3个部分.

2.1.1 考生因素

HoCDF使用向量来描述一个考生对不同知识点的掌握程度，即知识点掌握程度向量.向量中的每一个维度的数值都在[0,1]之间，表示考生对一个知识点的掌握程度.例如sn=(0.3,0.7)表示考生对第一个知识点掌握程度较差，对第二个知识点掌握程度较好.

2.1.2 试题因素

HoCDF使用向量来描述一道试题中不同知识点的难度，即试题难度向量.向量中的每一维度的数值都在[0,1]之间，表示一个知识点的难度.例如：em=(0.2,0.8)表示第一个知识点的难度较低，而第二个知识点难度较高.试题掌握程度表示考生对试题的实际掌握情况，且为一个连续值([0,1]).试题观测分数表示试题的得分，在客观题中为二分类的值({0，1}),在主观题中为连续值([0,1]).

2.1.3 交互函数

针对上述的考生因素和试题因素，层次认知诊断框架需要拟合以下3层关系以实现假设1：

·考生知识点掌握程度向量sn和试题掌握程度ρnm的关系.

·试题掌握程度ρnm和试题观测分数Rnm的关系.

·客观题和主观题之间的关系.

为此需要通过设计交互函数去实现这一目的.但是由于无法直接观测到考生的知识点掌握程度以及试题掌握程度，因此通过设计具体的函数去探究这一关系是一个非常复杂的问题.然而神经网络近似连续函数的能力已经在许多领域得到证明[12-13]，针对本文中的假设1，通过神经网络作为交互函数，将sn、ρnm及Rnm设置为网络中关键节点，从而搭建出特定的网络结构，从数据中有效地学习出上述三层关系.

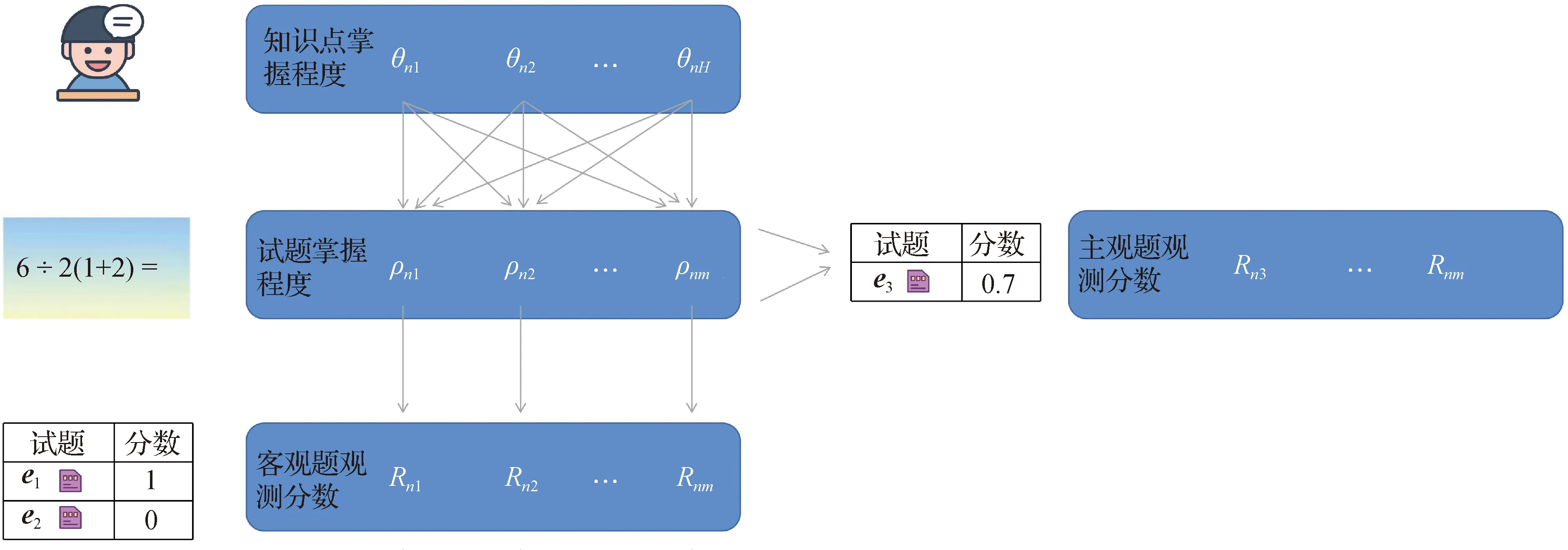
图3 基于层次观测的认知诊断框架Fig.3Hierarchical observational-based cognitive diagnosis framework

2.2 基于层次观测的认知诊断模型

如图4所示，基于HoCDF，本文从观测角度实现不同试题类型的联合建模，实现了一个具体的层次观测认知诊断模型.

图4 基于层次观测的认知诊断模型Fig.4Hierarchical observational-based cognitive diagnosis model

每个考生是由H个知识点组成的特征向量，并使用sn表示，sn的每一维表示考生对某一知识点的掌握程度θnh：

sn=sigmoid(Xs×A),

(1)

其中，sn∈(0,1)1×H,Xs∈{0,1}1×N,A∈RN×H,Xs表示学生One-hot，A表示学生嵌入向量矩阵.

试题因素包括试题知识点向量Qm,知识点难度cmh.试题知识点向量Qm的每一维表示试题中是否考核该知识点：

Qm=sigmoid(Xe×Q),

(2)

其中，Qm∈{0,1}1×H,Xe∈{0,1}1×M,Q=RM×H，Xe表示试题One-hot.

每道试题由一个特征向量em表示，em的每一维表示知识点的难度cmh：

em=sigmoid(Xe×B),

(3)

其中em∈(0,1)1×H,Xe∈{0,1}1×M,B∈RM×H,Xe表示试题One-hot，B表示试题嵌入向量矩阵.

为了对神经网络的输入层建模，受NeuralCD[5]的启发，将网络的输入层表示为：

X=Qm·(sn-em),

(4)

其中·表示逐点乘积.

以下是4个神经网络全连接层(其中f4为增加的不含激活函数的单层网络)，连接在输入层之后:

(f1=φ(W1XT+b1),

f2=φ(W2f1+b2),

f3=φ(W3f2+b3),

f4=W4XT+b4,)

(5)

其中φ是激活函数，并且W4的维度固定为知识点的数量H.

在生成考生分数的过程中，主客观题共享隐藏层f1,f2,f3和f4.接下来，将进一步生成试题掌握程度以及主观题分数：

ya=ρnm=f5=φ(0.5(f4+f3)),

(6)

其中φ是激活函数，ya表示主观题的预测分数Rnm,ρnm表示试题掌握程度.

为了充分应用假设1，本文中采取了极限情况，即认为试题掌握程度与主观题观测分数是一致的.然后，通过同时使用隐藏层和输出层，进一步模拟从试题掌握程度ρnm获得客观题分数的过程：

f6=φ(W5f5+b5),

f7=φ(W6f6+b6),

(7)

yb=φ(W7f7+b7),

其中，φ是激活函数，yb表示客观题的预测分数Rnm.

单调性假设[5,14]可以用来确保对考生和试题因素的可解释性.为了使模型满足该假设，本文采用了一个简单的策略：将W1，W2，W3，W5，W6，W7的每个元素限制为正[5].HoCDF的损失函数结合了均方误差和交叉熵损失函数：

(8)

其中:ma表示主观题数量，ra表示主观题的真实标签，mb表示客观题数量，rb表示客观题的真实标签，ya和yb分别表示主观题和客观题的预测分数.训练后，sn和em的维度值分别表示考生的知识点掌握程度θnh和知识点难度cmh.HoCDF的算法示例如算法1所示.

算法1HoCDF

输入:Q矩阵，试题one-hot，考生one-hot

输出:考生向量sn,试题向量em,试题预测分数ya和yb

1. 初始化考生矩阵A,试题矩阵B

2. for all (sn,em)∈训练集do

3. for = 1, 2, …, 32 do

4. 根据式(1)～(3)计算sn,Qm,em

5. 根据式(4)对神经网络的输入层X进行建模

6. 将X输入神经网络，根据式(5)和(6)建模试题掌握程度ρnm

7. ifem∈主观题then

8. 根据式(6)预测主观题分数ya

9. else

10. 根据公式7预测客观题分数yb

11. end if

12. end for

13. 根据式(8)，分别使用反向传播算法更新网络参数

14. end for

15. return考生向量sn,试题向量em,试题预测分数ya和yb

3 对比实验

3.1 数据集及实验设计

模型由PyTorch使用Python实现，并在具有Corei9-10900K 3.7 GHz、RTX3090GPU和128 GB内存的Linux服务器进行了一系列的实验以评估所提出的模型.

实验在两个真实世界的数据集[4]上进行，这两个数据集来自于高中考生的两个期末数学考试，每个数据集由一个分数矩阵和一个由教育专家给出的Q矩阵表示.数据集的构成如表1所示.图5是Q矩阵的预览，展示了试题中的知识点分布情况.为了观察模型在不同稀疏性水平下的性能表现.本文构建了不同大小的训练集，分别占每个考生得分数据的80%、60%、40%和20%.

表1 数据集的相关统计

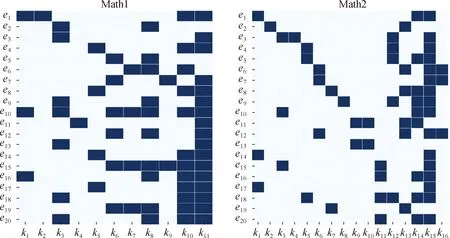
图5 Q矩阵预览Fig.5A preview of the Q-matrices

3.2 网络规范

3.3 评价指标与对比方法

由于无法观测到考生对知识点的实际掌握程度，通过预测考生在每个主观题和客观题上的得分验证HoCDF的有效性[16].使用的评价指标是平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE).选择三种机器学习方法和两种深度学习方法作为基线方法：

1) IRT(item response theory)[17]是一种教育心理学中对考生建模的方法.它是一种模拟考生的潜在特征、试题难度和试题区分度的认知诊断方法.

2) DINA(deterministic input,noisy and-gata)[18]是一种经典的认知诊断模型.在Q矩阵的帮助下，DINA通过考虑失误和猜测的因素，对考生的知识点掌握情况和试题进行建模.

3) NMF(non-negative matrix factorization)[19]是一个潜在的非负因子模型.该方法可以实现对考生潜在能力的建模.

4) DeepFM(factorization-machine based neural network)[20]基于因子分解机和前馈神经网络进行知识点间的交互，以实现对考生成绩的预测.

5) NeuralCD(neural cognitive diagnosis)[5]是利用神经网络捕捉考生与试题之间的关系，从而诊断考生的知识点掌握程度.

本文首先将HoCDF与其他用于考生建模的基线方法比较，以验证模型的综合性能.接着，分别进行了HoCDF对客观题和主观题的预测，以展示模型对主客观题预测的性能.然后，在模型内进行消融实验以验证文中提出的假设的有效性.接着，通过展示考生在各个知识点上的掌握程度分布的箱型图，验证模型可以更加清晰地诊断出不同考生对同一知识点的掌握程度差异.最后通过案例分析说明模型的可解释性和准确性.

3.4 实验结果分析

3.4.1 不同数据集比例下的预测性能

下面将展示每个模型在不同数据集比率方面的有效性，误差条是每个模型的5次评估运行的标准差.图6显示了所有模型在预测考生成绩任务上的实验结果.首先可以观察到：HoCDF在两个数据集上MAE均优于其他基线方法，RMSE优于大部分基线方法，验证了HoCDF的有效性.与DeepFM相比，随着训练数据的增加，本文提出的模型可以得到更加充分的训练.其次，尽管模型是基于神经网络来捕捉考生与试题之间的交互作用，但是当训练数据稀疏时，HoCDF保持了良好的预测性能.接着，虽然DeepFM通过深度学习利用了考生的潜在特征和试题的语义特征，但HoCDF(忽略语义特征)在不同的测试集比率下优于竞争方法.最后，深度学习方法明显优于传统方法，但不同的深度学习方法在RMSE方面的性能是相近的.

图6 不同数据集比率下的预测性能Fig.6Prediction performance with different dataset ratios

3.4.2 客观题和主观题的预测性能

为了检验该框架对客观题和主观题的预测效果，在20%的测试比例下进行了实验，误差条是每个模型的5次评估运行的标准差，实验结果显示在图7中.与基线方法相比，HoCDF在主观题和客观题上均取得了较好的预测性能.与NeuralCD相比，模型对于主观题和客观题的预测性能均得到了明显提升，并且针对主观题的预测性能更加优越，主要是由于HoCDF区分了主观题和客观题的差异.

3.4.3 消融实验

为了验证假设1和假设2的有效性，本文进行了一组消融实验，设置了3个对照组：剔除假设1、剔除假设2以及同时剔除两种假设的基线组，并以“HoCDF-假设1”、“HoCDF-假设2”和“HoCDF-假设1，2”表示.为了剔除假设1，文中将主观题视为客观题来处理(将部分正确的回答标记为错误[4]).为了剔除假设2，对照组剔除了不含激活函数的单层网络.

实验结果如图8所示，相较于同时剔除两种假设的基线组，通过分别增加不同假设，模型在不同比例的训练集下预测考生成绩的性能均得到了提升.但是在MAE指标上，相较于HoCDF，假设2对模型的性能已经无法造成较大影响，模型性能已达上限.

图7 客观和主观试题的预测性能Fig.7Prediction performance for objective and subjective problems

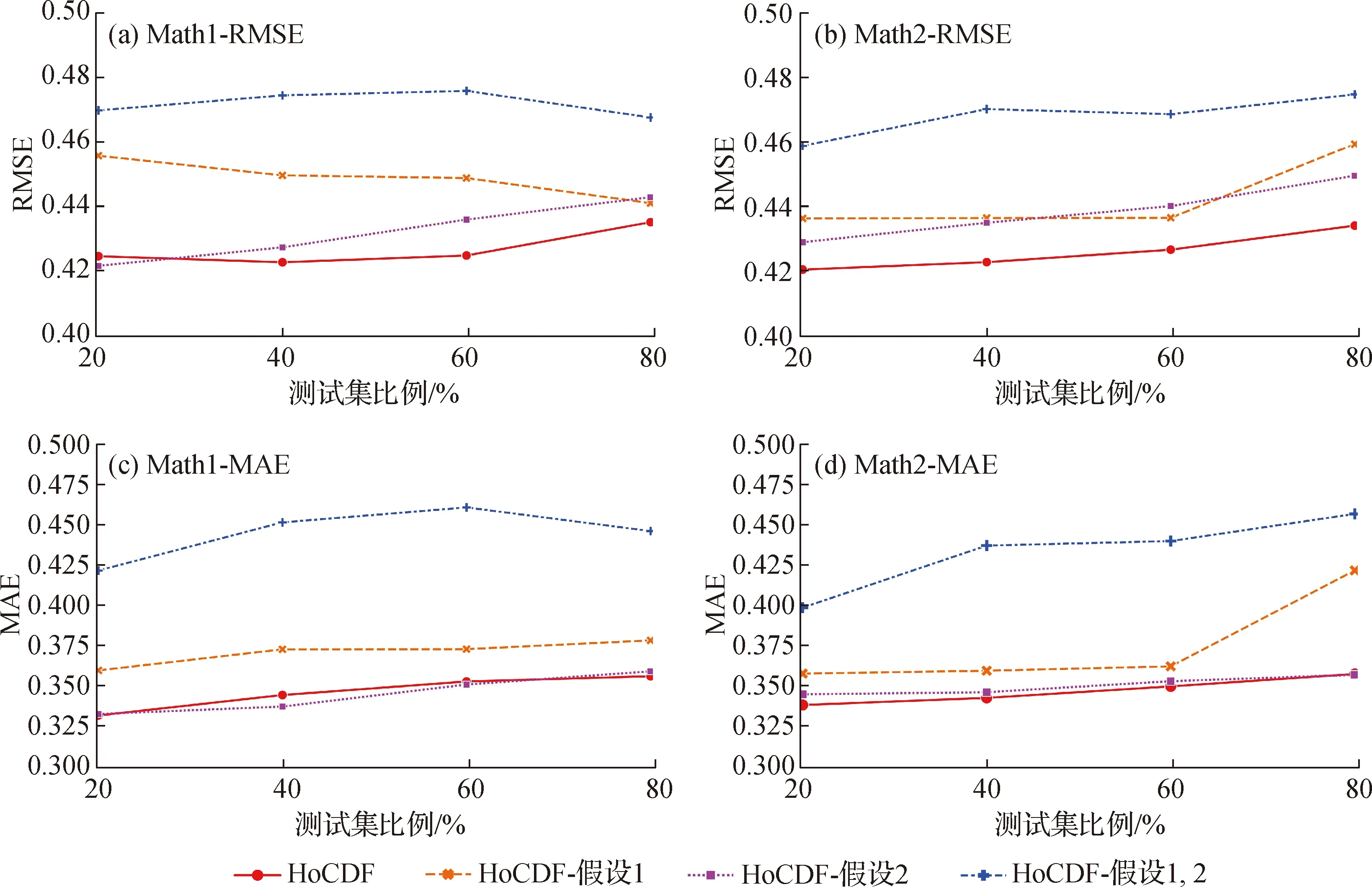
图8 消融实验Fig.8Ablation experiment

3.4.4 考生在各个知识点上的掌握程度分布

在上一节中已经展示假设1和假设2对模型性能的影响.然而通过增加额外的单层网络，主要是为了提高对考生嵌入向量的学习效果，从而更加充分的诊断出不同考生对同一知识点的掌握程度差异.为此，本文在20%的测试比例下进行了实验，并在图9中展示了所有考生在各个知识点上的掌握程度分布的箱型图.

图9 考生在各个知识点上的掌握程度分布Fig.9The distribution of examinees’ proficiency of each knowledge concept

如图9所示，在剔除假设2后，考生对各个知识点的掌握程度分布在一个较小的区间内，考生的能力波动较小.显然无法清晰地区分不同考生对同一知识点的掌握程度差异，这使得模型并没有充足的可解释性.通过增加假设2，考生对各个知识点掌握程度的分布区间均得到了不同程度的提升.因此，HoCDF可以提高对考生嵌入向量的学习效果，更加清楚地区分不同考生对同一知识点的掌握程度差异.因此基于神经网络的认知诊断模型的可解释性得到了一定程度的提升.

3.4.5 案例分析

图10给出了HoCDF诊断报告的具体案例分析.案例分析表明，HoCDF可以给出考生对知识点的具体掌握程度并清晰地区分出考生对知识点的掌握程度和知识点难度之间的差异性.

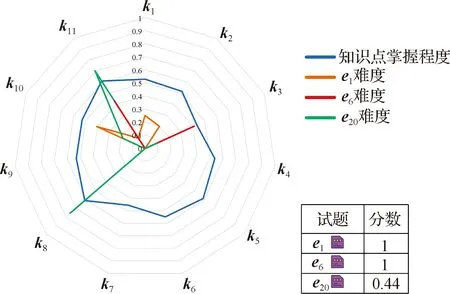
图10 HoCDF案例分析Fig.10Case study for HoCDF

进一步分析了考生的答题记录可知，考生的知识点掌握程度达到了e1、e6中各知识点的难度要求.但是仅部分满足e20中的知识点的难度要求.从图中可以看出，当考生的知识点掌握程度满足了试题的要求时，他更有可能做出正确的反应，可见本文的模型具有较强的可解释性.根据诊断结果，考生可以更好地掌握其现状，帮助教师给出个性化的补救建议以及设计有针对性的教学计划.

4 结 论

认知诊断旨在发现考生对特定知识点的掌握程度，从而实现对考生成绩的预测.然而，目前关于认知诊断的研究主要集中在试题中所考察的多个知识点之间的相互作用上，并没有充分探索试题类型之间的差异，而基于深度学习的认知诊断模型往往不能清晰地诊断出不同考生对同一知识点的掌握程度差异.HoCDF通过观测得分的差异性区分主观题和客观题，从而实现不同试题类型的联合建模，并且通过增加不含激活函数的单层网络作为额外通路，更加充分地诊断出不同考生对同一知识点的掌握程度差异.HoCDF的性能远优于其他考生建模方法，不仅能成功诊断出考生对知识点的掌握程度，而且可以更加有效地实现考生成绩预测.本文提出的方法没有对知识点进行特殊处理，可以进一步考虑有针对性地构建知识点之间的关系图，用以提高模型的有效性.