一种基于单形空间缺失数据的补全方法

刘 冰，李玮琦

（达州职业技术学院人工智能学院，达州 635001）

0 引言

成分数据是一种具有比例结构的多维数据，其数学形式定义为

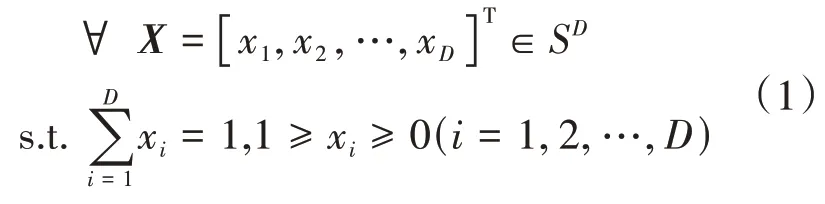
则称向量X为D维成分数据［1］，向量空间SD为单形空间，其中X中的每一个元素xi表示其在整体中所占的比重。相较于普通数据而言，成分数据除了用于分析整体中各部分数据间的相对关系外，还有利于揭示普通数据所隐藏的相对信息，在诸如社会学、经济学、气象学、地质学、医学等领域都有十分广泛的应用［2-4］。

由公式（1）可以看出，单形空间中的数据受到两个条件的限制，一个是有界约束，另一个是定和约束，而现有一般的统计分析方法对被分析数据是没有约束要求的。显然，这就导致现有一般的统计分析方法在单形空间中无效，一个最主要的原因在于单形空间中数据的协方差矩阵通常是奇异矩阵，其含义与普通的数据不同［5］；另一个原因在于单形空间中的数据总体一般不满足多元正态分布的假设，这就会导致建立模型十分困难。为了能运用现有一般的统计分析方法去分析单形空间中的数据，通常的做法是先进行预处理，即经过一定的变换使之成为无约束数据。文献［1］首次提出通过对成分数据的对数比变换建立成分数据的逻辑正态分布模型，有效地解决了现有一般的统计分析方法对单形空间中数据有界定和约束的限制，但建立的模型对数据的解释性较差；文献［6］提出了一种新变换，即对称对数比变换，该方法能很好地解释数据，但在某些情况下容易造成变换后的数据间存在较高的冗余性，从而损失部分数据信息；文献［7-8］在此基础上又进行了改进，即对称等距对数比变换（isometric logratio transformations，ILR），但该方法对数据的完整性要求较高，若存在数据缺失，当补全为0时会造成变换后的数据为无穷的情况，显然失去了实际的意义。对于成分数据的缺失值补全，目前一般采用单形空间均值（SM）补全法、极大似然补全法、期望最大填补法、k近邻补全法（KNN），等等。这些方法对于回答信息而言其实现较为容易，但稳健性差，结果偏差较大，补全后的数据冗余度高，缺少解释性。

消除变换后的数据冗余性的最有效方法是实现单形空间到欧氏空间的正交变换，为此，本文首先给出单形空间的代数运算体系，在给出文献［4，9-11］的相关变换过程的基础上，着重研究对于成分数据存在缺失值时通过对数比变换后存在的多重共线性数据的填补方法，并结合主成分分析法提出了一种较为有效的参考解决路径。

1 单形空间的代数体系

为了实现单形空间到欧氏空间的正交变换，本文给出单形空间对于向量的加法、数乘、内积以及距离的如下定义。

（1）向量的加法：对于任意X,Y∈SD，向量X,Y的加法运算⊕定义为

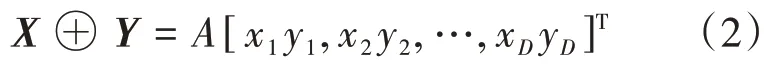
式中，A[.]为封闭运算，即

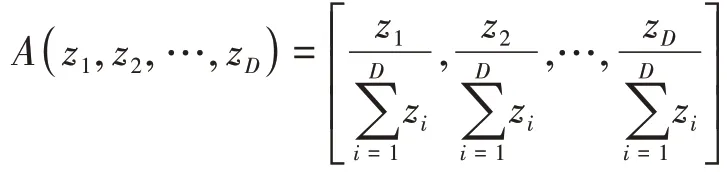
（2）向量的数乘：对于任意X∈SD，任意实数a∈R，a与向量X的数乘运算⊗定义为

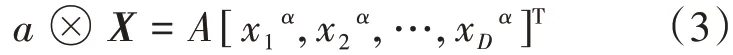
（3）向量的内积：对于任意X,Y∈SD，向量X,Y的内积定义为

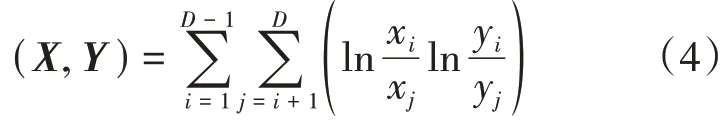
（4）向量的距离：对于任意X,Y∈SD，向量X,Y的Aitchison距离［10］定义为

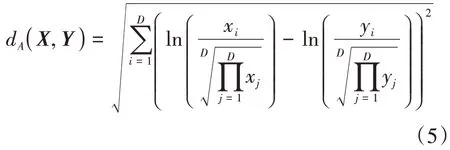
2 成分数据的缺失

在实际工作中，待分析处理数据集中某些数据或属性值缺失的原因是多方面的，或者是调查者基于主观的判断认为不重要而丢弃某些数据；或者是由于客观的问卷设计存在瑕疵、录入失误、受访者拒绝回答而没能采集到某些数据；或者是在原始数据的存储过程中，由于设备的故障造成存储数据的不全或失败而丢失某些数据等，使得没能满足设计预期获得详细而全面的资料数据，显然，如果缺失数据占比较大，对于后续的数据分析处理会造成难以估计的影响。

从式（1）易知，若一个成分向量中只有一个元素值缺失，即可根据定和限制求出该缺失值，因此一般来说，成分数据的缺失值是指某个样本或属性值中至少有两个或两个以上的缺失值。其数学形式化定义如下：

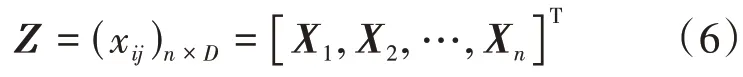
若某个向量Xk（k= 1,2,…,n）中至少有两个元素值存在缺失，则称Z为缺失数据矩阵。

3 缺失数据的补全

由于主客观等因素的影响，经常会碰到待分析处理的数据集中某个数据或某些属性值出现为零或缺失的情况。对于前者，通常的做法是将其处理为缺失值；而对于后者，一般先要考虑缺失数据的占比情况，若某行（列）缺失数据比超过90%，一般进行剔除处理，或重新进行该行（列）数据的采集。对于缺失数据比小于90%的情况，则对缺失数据进行某种策略的填补。—种经典的填补方法是基于k近邻（KNN）方法［12］，即用通过某缺失值的k个最近邻样本信息来估算该缺失值；另一种是把缺失值当作一类随机变量或者隐变量，建立概率隐变量模型，然后通过EM、VI（Variational Inference）或者MCI（Monte Carlo Inference）来估计缺失值的分布，具体做法是：

对于式（1），进行如下的处理：

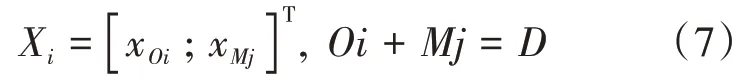
其中，xOi为非缺失值数据，xMj为缺失值数据，则缺失值xMj的分布估计为

然后计算该分布的期望值，并将其置为缺失值的估计值。

对于简单的模型，其解析解可用EM 算法求解；若模型复杂，则可借助MCI 去进行逼近求解，但无法解决结构带来的不实用的问题。

此外，对于多元线性回归模型，若变量之间线性无关，还可采用回归估计法对缺失值进行填补。但变量之间完全线性无关仅仅具有理论上可能，在实际情况下，变量之间往往存在多重共线性，若直接采用回归估计法，其估计结果会与实际情况相去甚远。

对于多重补全法，文献［9-11，13］给出的方法较有代表性，下面作简要介绍：

3.1 非对称对数比变换

对于式（1），定义如下变换：

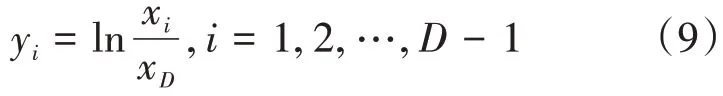
其逆变换式为xD=，进而有：

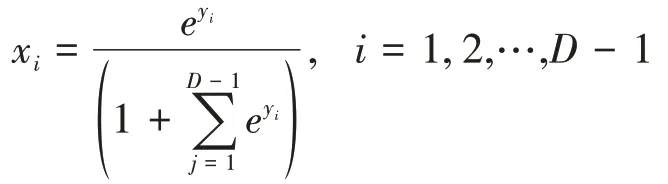
从式（9）中可以看到，该变换是一个从单形空间SD到欧氏空间RD-1上的线性变换，而非正交变换，变换后的yi与变换前的xi不具有一一对应的关系，即存在非对称关系，这就会导致建立的模型不能合理准确地解释数据。

3.2 对称对数比变换

针对非对称对数比变换存在的缺陷，张尧庭［6］在《成分数据统计分析引论》中提出了一种新变换，使得变换后的yi与变换前的xi具有了一一对应的关系，即存在对称关系，这就使得建立的模型具有了一定的可解释性。其具体变换式如下：

对于式（1），定义如下变换：

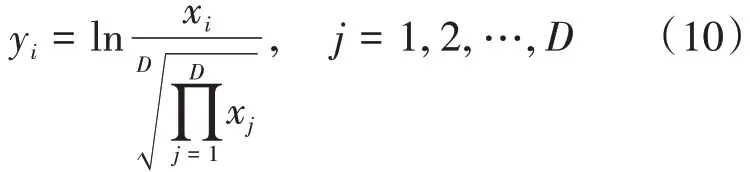
其逆变换式为xD=，进而有：

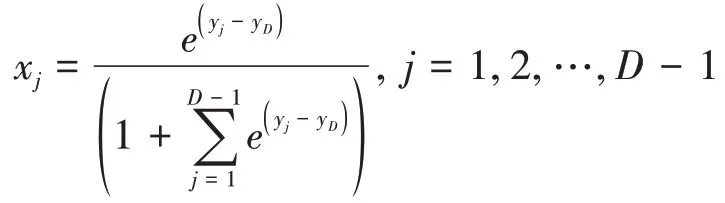
从式（10）看到，该变换是正交变换，但当0＜xi＜1 时，∀[α1,α2,…,αD]T∈SD,αiyi≠0，即变换得到的数据存在一定的相关性，导致了变量间协方差矩阵不满秩，从而使得基于协方差结构的统计方法无效，在实际应用中，应当避免使用该变换对成分数据进行预处理。

3.3 对称等距对数比变换

文献［4，11，13］又在对称对数比变换基础上进行了改进，即对称等距对数比变换（isometric log-ratio transformations，ILR），具体如下：

对于式（1），定义如下变换：

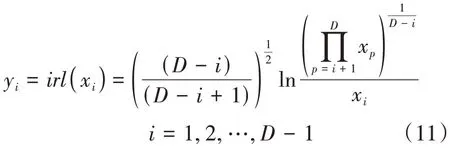
容易得出：式（11）的逆变换式为

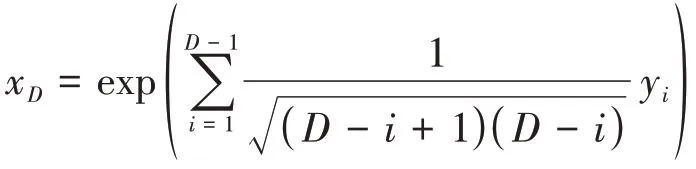
进而有：

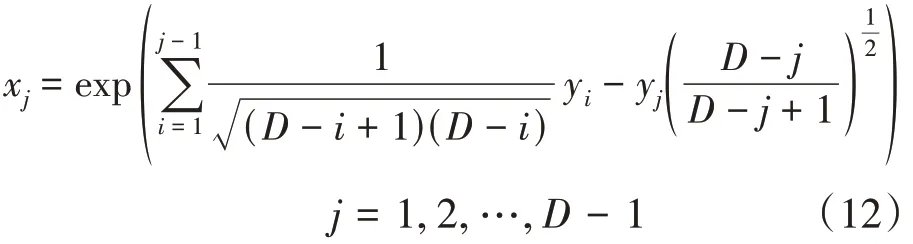
从式（11）可以看出，该变换实现了从单形空间SD到欧氏空间RD-1的正交变换，确保了在变换后的空间中运用传统的统计分析方法进行合理的模型建立。但在xi= 0时，对应的yi的结果将为无穷，失去了实际的意义，对后续的进一步分析处理造成了障碍。

4 成分数据的补全

一般情况下，对于缺失数据不宜贸然进行删除处理，通常需要采用某种方法进行补全操作。常用的方法有：均值补全法、极大似然估计法、多重补全法等，其中多重补全法是通过估计出待补全的值加上不同的噪声来得到补全值。对于成分数据缺失值的补全，Hron 等［12］提出的k 近邻法较有代表性，该方法是通过用Aitchison 距离来寻找到含缺失值样本的k 个近邻，并用该k 个近邻的中位数来进行初始补全，然后用最小二乘法来进行迭代补全。本文在前面定义的单形空间的加法运算⊕以及数乘运算⊗的基础上结合文献［12］的方法，提出一种基于单形空间缺失成分数据的补全方法，同时运用主成分分析法，处理将成分数据变换为一般数据后可能存在的多重共线性的情况。

4.1 多重共线性

在进行多元回归分析时，若某些解释变量之间存在严格或近似的线性关系，其样本点或属性值的一个微小改变都会极大地扰动回归系数的估计值，使得回归系数极不稳定［14］。因为某些解释变量之间存在的强相关关系将极大地降低ZTZ的可逆性，大多数情况变得不可逆，即使通过某种计算使其变得可逆，其逆矩阵的特征值也往往会较大，导致标准误差值也较大，进而降低了参数估计值的精度，无法得出稳定的回归模型，回归系数及符号也与实际情况相去甚远。

检测多重共线性的方法主要有：

（1）通过计算自变量间的相关系数与显著性来进行判断，即若某些变量间的相关系数显著，则认为它们之间可能存在多重共线性问题。

（2）使用回归分析中的方差膨胀系数（Variance inflation factor，VIF）值来进行判断，VIF的计算公式为VIF=1/ (1 -)。其中，Ri为负相关系数。自变量之间共线性程度与VIF 值存在较强的正相关关系。根据Hair（1995）标准，当VIF≤10 时，模型的多重共线性较弱；当10 ＜VIF≤100 时，模型的多重共线性较为严重；当VIF＞100时，模型的多重共线性很严重。

（3）容忍值（Tolerance）法，也是较为常用的方法。其计算公式为Tol＝1/VIF。显然，其与方差膨胀系数法的判定标准相反，自变量之间共线性程度与Tol值存在较强的负相关关系。在实际中，通常为Tol指定一个阈值，确保小于阈值的变量间的相关系数矩阵可逆，使回归系数的估计值具有较强的稳定性。该方法的缺陷在于Tol阈值的确定存在随意性，没有一个统一的标准。

（4）主成分回归法，对于矩阵（6），设ZTZ的特征值为λ1≥λ1≥… ≥λn＞0，称h=λ1/λn为ZTZ的条件数，一般地，若h＜100，则认为模型的多重共线性程度较小；若100 ＜λ1＜1000则认为模型的多重共线性程度较强；若h＞1000，则认为模型的多重共线性程度严重。

需要说明的是，在现实工作中，获得的数据集一般都存在多重共线性，只是程度不同而已，对于共线性程度较小或一般的问题可以不必采取措施。另外，如果学得模型的拟合度好，也可不需处理多重共线性问题。

4.2 单形空间上的均值补全

根据公式（5）易知，若两个样本各自成分数据子集相似，则它们之间的Aitchison 距离可以用其对应子集的Aitchison 距离大约表示。即dA(xi,xj)≈dA(XMi,XMj)≈dA(XOi,XOj)，其中 ：XMi,XMj和XOi,XOj分别是样本xi,xj各自所对应的缺失值和确定值成分数据子集。

下面根据第2节的相关定义及文献［12］的方法给出xi的某一缺失成分xmi∈XMi，m∈M的补全步骤：

（1）根据Aitchison 距离找到含缺失值xi相应子成分XMi的k（k＜n）个最近邻， 并记为其对应的k个全样本依次为。

（2）根据定义1 和定义2，计算出k个全样本的均值：

（3）求出xmi的补全值：

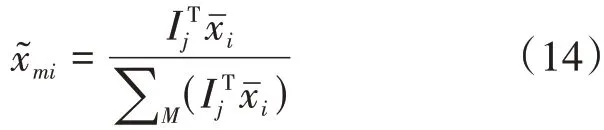
其中：Ij=(0,…,1,…,0)T∈Rn的第j个元素为1,j= 1,2,…,n。

4.3 基于主成分的补全

在大多数情况下，在单形空间上由子成分的Aitchison 距离对缺失值进行均值补全后的成分数据存在多重共线性，基于4.1 节所述，下面采用主成分回归分析法对上节初始补全后的成分数据再次进行修正补全，主要步骤如下：

（1）将含有缺失成分的样本xi和其k个最近邻样本xi[1],xi[2],…,xi[k]组成一个单形空间矩阵，并将缺失值xmi初始补全后的变换到第1 行第1列，记为：A(k+1)×D。

（2）根据公式（11），将单形空间矩阵转换为欧式空间矩阵，如下所示：

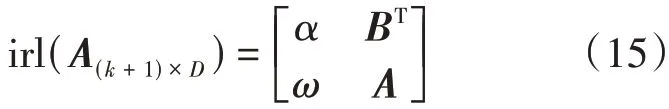
其中，α= irl(x͂mi)，A为一k×(D- 1)阶矩阵，令：

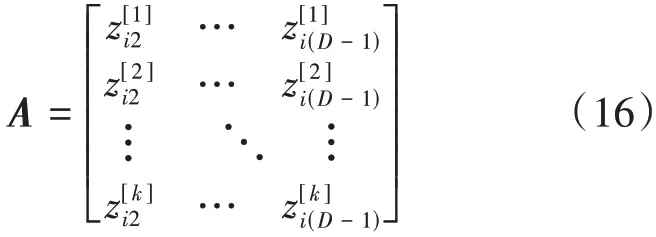
（3）对矩阵A做主成分分析，其协方差矩阵记为Λ=，其中，zu,zv为A的行向量，为A的行向量均值。

（4）计算Λ的前p个主成分，依次为λ1≥λ1≥…≥λp≥0，则响应变量Y与间的关系为

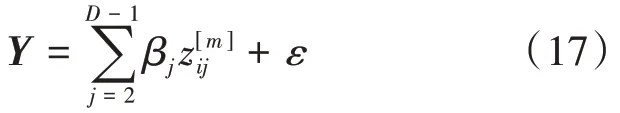
其中：m= 1,2,…,k,ε为误差项。

（5）通过上式得到βj的估计值，计算到缺失值xmi的补全值为

（6）运用公式（12）将数据xmi还原为成分数据，并通过第（1）步将其调回到原始位置。

5 评价与比较

5.1 评价指标

为了有效地评价上述方法对数据集中缺失值的补全效果，本文采用正规化方均根差（the normalized root mean squares error，NRMSE）作为判别准则，即：

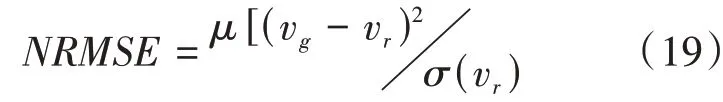
其中，vg为补全值，vr为真实值，μ(.)为均值，σ(.)为方差。NRMSE值的大小反映了真实值与补全值之间差距，若NRMSE值较大，则说明补全值与真实值存在较大差距；若NRMSE接近于0，则说明补全值非常接近真实值。

5.2 比较分析

为了验证前述方法的有效性，选用文献［1］中Hongite 数据，该数据集包含25个样本，每个样本包含5 个特征：ablite，blandite，cornite，daubite，endite，根据4.1 节所述计算得到条件数h=2747.238＞＞1000，即认为该数据集存在严重的多重共线性。下面假定该数据集的ablite 和cornite 特征数据缺失，分别运用k近邻补全法（KNN），单形空间均值（SM）和主成分补全法（PCA）对缺失值进行补全，得到比较结果见表1。

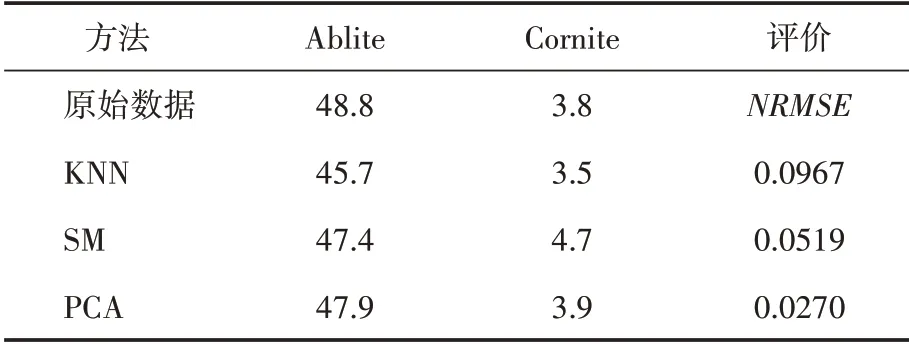
表1 KNN，SM和PCA补全操作比较结果表

从表1可以看出，当条件数h＞＞1000时，用PCA 方法进行补全的结果最好，KNN 的补全结果最差。

根据文献［10］的结论模拟100 个5 维的成分数据x～N5φ(μ,∑)，其中μ=(0,0,0,0)T，∑是一个主对角线上全为1，其余全为p的4 阶方阵。在假定p的取值分别为0.3、0.7、0.995，缺失率（MR）分别为10%、20%和30%情况下，分别运用KNN、SM 和PCA 方法进行缺失值补全，并用NRMSE进行评价比较，结果如图1所示。

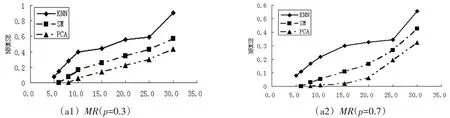
图1 MR与P分别取值时三种方法的补全比较结果

其中，在图1 中的图a1～a3 是在MR不同p一定时三种方法的补全比较结果，图b1～b3 是在p不同MR一定时三种方法的补全比较结果。

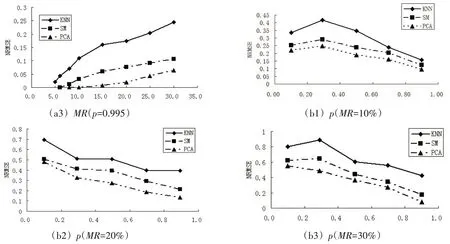
图1 MR与p分别取值时三种方法的补全比较结果（续）

从图b1 与图b2 中可以看出，PCA 比KNN，SM 的结果都要好。这三种补全法在MR一定时，p与NRMSE呈负相关关系，也就是说若数据间的多重共线性程度越大，无论哪种方法的补全效果都越好。而在p一定时，三种方法的MR与NRMSE呈正相关关系。作为初始的补全法，KNN 法明显比SM 差，随着MR的増大，结果会更差。但在MR变大时，PCA 法明显比SM 效果好，随着MR的増大，结果会更明显。

6 结语

基于单行空间完备的代数体系提出的等距对数比变换是一个正交变换，该变换既克服了非对称对数比变换改变内积及距离等几何概念的缺陷，同时，又避免了对数比变换导致的多重共线性给多元分析方法带来的不利影响。对于含有缺失值的多元数据来说，无论是基于模型还是基于距离，多变量补全法比单变量补全法结果更为准确：在单形空间上先进行均值补全，然后运用等距对数比对补全后的数据进行变换，最后再对变换后的数据运用主成分法进行第二次补全，实例分析表明，再次运用主成分法进行二次补全要比其他方法的效果更好。