研究2022年全国高考抽象函数问题
胡 潇 李昌成
(1.江苏省海门中学 226199;2.新疆乌鲁木齐市第八中学 830002)
2022年全国高考多份试卷将抽象函数作为压轴选择题,入手难,突破更难.究其原因,教材没有相关内容,至多从正余弦函数迁移理解习得.抽象函数很灵活,少套路,尤其是自变量取值.
1 基本理论
结论1 (周期性)若f(x)(x∈R)满足f(x+a)=f(x+b),则f(x)的周期为T=|a-b|.
结论2(周期性)若f(x)(x∈R)满足f(x+a)=-f(x),则f(x)的周期为T=2|a|.


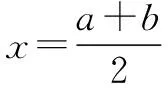
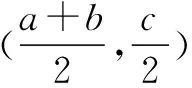
结论7(对称性)若f(x)(x∈R)满足f(x+a)是偶函数,则f(x)关于直线x=a轴对称.
结论8(对称性)若f(x)(x∈R)满足f(x+a)是奇函数,则f(x)关于点(a,0)中心对称.
结论9若f(x)(x∈R)满足x=a是f(x)的一条对称轴,点(b,0)是f(x)的一个中心对称,那么f(x)的周期为T=4|a-b|.
2 真题研究

C.f(-1)=f(4) D.g(-1)=g(2)
分析本题主要考查导函数与原函数的关系,抽象函数的对称性及奇偶性.联想起正余弦函数的导数关系,原函数与导函数奇偶性对换,对称轴与对称中心互相转化等,从而衍生出周期性,由于是两个相关函数,解答时要兼顾二者,互为补充.
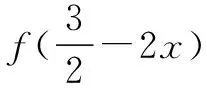
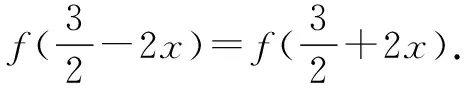
①
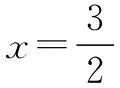
因为g(2+x)为偶函数,
所以g(2+x)=g(2-x).
②
由结论5得g(x)关于直线x=2对称.
所以f(x)关于点(2,h)对称.
③
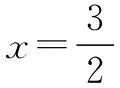
④
因此A不正确.
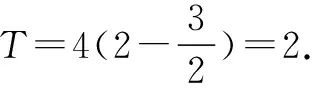
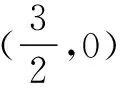
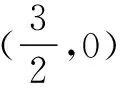
综上,答案为BC.
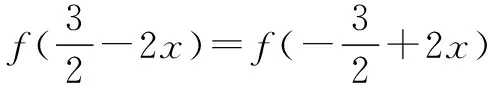
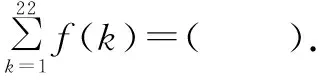
A. -21 B. -22 C. -23 D. -24
分析本题是考查两个抽象函数的对称问题和周期性问题,以f(x)的函数值之和为出口.首先要考虑消去或代换掉g(x),为实现这目标必须充分利用“f(x),g(x)的定义域均为R”这一条件,对自变量合理赋“值”.从已知的两个关系式能发现函数的对称性,进而分析出函数的周期性.已知的轴对称性要和已知关系式紧密结合起来,才能起到桥梁作用.
解析因为y=g(x)关于直线x=2对称,
所以g(2-x)=g(x+2).
⑤
因为g(x)-f(x-4)=7,将该关系式中x代换成x+2,得g(x+2)-f(x-2)=7.(※)
即g(x+2)=7+f(x-2).
⑥
因为f(x)+g(2-x)=5,
⑦
将⑤代入⑦,得f(x)+g(x+2)=5.
⑧
将⑥代入⑧,得f(x)+[7+f(x-2)]=5.
即f(x)+f(x-2)=-2.
⑨
令x=22,得f(22)+f(20)=-2.
令x=21,得f(21)+f(19)=-2.
所以发现连续4项和为-4.
⑩
所以f(22)+f(21)+…+f(4)+f(3)=-20.
在⑦中令x=0,得f(0)+g(2)=5.
因为g(2)=4,所以f(0)=1.
在⑨中令x=2,得f(2)=-2-f(0)=-3.
在g(x)-f(x-4)=7中,将x代换成x+4,得
g(x+4)-f(x)=7.
由结论6知,y=g(x)的图象关于点(3,6)中心对称,又函数g(x)的定义域为R,所以g(3)=6.
在⑧中令x=1,得f(1)=5-g(3)=-1.
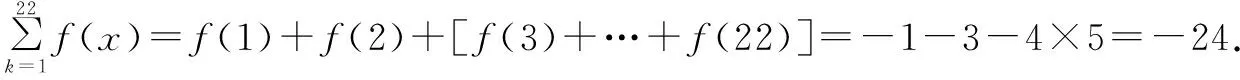
评注在(※)处的代换目标性很强,因需代换,需要考生瞻前顾后.由题设的轴对称性可以得到无数的关系式,此时应根据需要选择⑤,当然也可以选择其它关系式,就会导致后期解题走向变化,有兴趣的同仁可以试试.通过周期性完成20项求和后,解答陷入“僵局”,此时思维转换,以退为进,着手研究g(x),从它的对称中心找到突破点,这一点对考生来讲十分困难.整个解题过程目标一定明确,自变量选择具有任意性,这是本题难点所在,需要学生有较高的思辨能力.
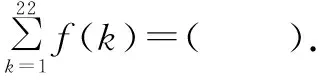
A. -3 B. -2 C. 0 D. 1
分析此题和上一题显然是姊妹篇,但是风格迥然.没有明显的对称性、周期性条件,需要考生在神秘的关系式“f(x+y)+f(x-y)=f(x)f(y)”中去探索解题所需.赋值法是解决这类问题的法宝.条件“f(1)=1”是消元的唯一出口,也为赋值提供了依据.但赋值方向不明,解答充满着变数.
解析因为f(1)=1,所以令y=1得f(x+1)+f(x-1)=f(x)×f(1)=f(x).
进而f(x+1)=f(x)-f(x-1).
f(x+2)=f(x+1)-f(x).
f(x+3)=f(x+2)-f(x+1).
由结论2知,f(x)周期为T=6 .
下面计算前六项.
在f(x+y)+f(x-y)=f(x)f(y)中,令x=1,y=0得f(1)+f(1)=f(1)f(0).又f(1)=1,故f(0)=2.
故f(1)+f(2)+…+f(6)=0.

所以选A.
评注在处找到题目的递推关系,借助此式建立周期是一个难点.在未有心理预期的情况下连续两次迭代不易想到,只有坚信问题与周期有关方可持续迭代,也需要学生熟悉结论2,否则迭代是茫然的.赋值和迭代是解答本题的重要手段.这是一个创新的抽象函数问题,与从前研究抽象函数的奇偶性手段相比,虽然都是赋值,但是本题迭代赋值还是很新颖的,对考生的能力要求很高.
解答这类有关抽象函数求值问题我们要充分利用自变量的任意性,对其进行赋值,逐步向目标靠近;熟练掌握抽象函数的对称性、周期性的多种定义衍生结论,不是记忆,而是理解;双抽象函数的内在关系要理顺,利用消元思想,各个击破;思路要开阔,不能寻求一种万能办法应对灵活多变的抽象问题,而是要系统关注每个函数、每个性质、每个特殊值;主动培养创新意识,积极应对新模式、新定义、新情景、新问题.

