随机微分方程的数值求解

刘永财，柏明花

(曲靖师范学院 数学与统计学院，云南 曲靖 655011)

0 引 言

随机微分方程中随机因素的存在使得求解方程的过程非常复杂，很多随机微分方程很难解出精确解，故数值求解具有重要意义，国内外涌现出大批学者对随机微分方程的数值法求解进行研究.刘涛[1]对随机微分方程的数值方法进行了系统的研究；王彩霞[2]研究了随机微分方程数值方法的稳定性与收敛性；李焕荣[3]不仅对随机微分方程数值求解方法进行研究，还研究了其应用；谢晓波[4]对几类随机微分方程与偏微分方程的数值解法进行了研究；陈晨[5]研究了随机微分方程解的存在唯一性与其数值方法的稳定性；张永强,卢俊香[6]研究了一类线性随机微分方程的解法；周迎春[7]研究了几种随机微分方程数值方法以及数值模拟；叶安[8]深入研究了伊藤随机微分方程的两种数值方法；汪勇[9]对Euler-Maruyama方法进行了细致的研究；Li Lei等[10]研究了基于高斯混合的随机微分方程的数值方法；Mustafa Bayram[11]研究了随机微分方程的数值模拟方法.本文在学者们的研究基础之上，对显式Euler方法、梯形Euler方法及显式Milstein方法进行研究，通过观察不同步长时的误差和运算时间来分析数值解的精度.

1 随机微分方程及其数值方法

1.1 It型随机微分方程

布朗(Brown)通过显微镜对液体中的花粉做出观察，发现它们作不规则运动.下面给出布朗运动的定义：

定义1 一个在[0，T]上的随机过程W(t),如果它连续的依赖于t∈[0,T]并且满足以下的三个条件：

(1)W(0)=0；

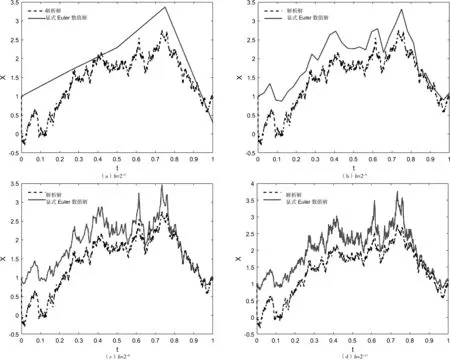
(2)对于0≤s

(3)对于0≤s

标准布朗运动的性质：

(1)P(W(0)=0)=1;

(2)∀t>0,h>0,△W(t)=W(t+h)-W(t)～N(0,h)

(3)∀t∈T,W(t)不可微.

由上可知，Brown运动处处连续，处处不可微，有着曲折的运动轨迹.

Wi=Wi-1+dWi,i=1,2,…,n,

图1 布朗运动轨迹图

常微分方程的一般形式是:

dX(t)=X(t)dt,t∈[t0,T]

(1)

随机微分方程与常微分方程最大的不同之处在于随机微分方程里面存在着随机因素，因此方程的求解就有不确定性，常微分方程并不能有效地描述这种不确定性系统，所以要对方程(1)进行适当的调整，即加入随机因素，使它能够把带随机干扰的现象反映出来，It型随机微分方程因为具有鞅性质而让其计算更加简便.

定义2 假设{X(t,w),0≤t≤T}是一个随机过程，{W(t),t≥0}是标准的Brown运动，对任一个划分

P={0=t0

对于如下形式的随机微分方程：

t∈[t0,T]

(2)

其中f:R+×Rn→Rn称为漂移系数，矩阵函数g:R+×Rn→Rn×m称为扩散系数，W(t)是m维Brown运动，X0是随机变量.

根据布朗运动的连续性可以把(2)写为下面的形式：

0≤t0≤t≤T.

1.2 Euler方法和Milstein方法

大部分随机微分方程的解析解是无法获得的，在实际应用中，实用的方法是在计算机上进行数值求解，即不直接求出y(t)的解析解，而是在随机微分方程的解存在的区间上，求得一系列点xn(n=1,2,…)上的近似值[5].到目前为止，有多种数值方法来求解随机微分方程，Euler方法以及Milstein方法是对随机微分方程数学模型进行数值模拟的两种便捷、高效的方法.

(1)显式Euler方法：

Xn+1=Xn+f(Xn)h+g(Xn)△Wn

(3)

其中，Xn是在tN=nh处的近似解，△Wn=Wtn+1-Wtn表示定义在区间[tn,tn+1]上的Wiener过程的增量，是服从N(0,△t)分布的相互独立的随机变量.

(2)梯形Euler-Maruyama方法：

(4)

而Milstein方法是求解随机常微分方程的具有一阶强收敛的方法[3]，显式Milstein方法如下：

(5)

2 数值算例

以如下齐次线性随机微分方程为例：

(6)

其中，X(t)是随机过程，λ和μ都是常数，W(t)是标准布朗运动.f(X)=λX(t)为漂移系数；g(X)=μX(t)为扩散系数.随机微分方程可能有无穷多个解，为了限定解，需要加入一个初值条件：X(0)=X0.

令λ=1，μ=1，X0=1，来求此方程的解析解，求解步骤如下：

(2)使用伊藤引理，得到d lnX(t)的随机微分方程(SDE)：

综上可以得出，类似方程(6)的随机微分方程的解析解通式为：

对于方程(6)，令λ=1，μ=1，X0=1，取N=2-11来估计方程的解析解，取时间步长h分别为2-2，2-5，2-8，2-11，利用MATLAB编码可以得到方程的解析解以及显式Euler方法求得的数值解，如图2所示：

图2 显式Euler法数值运算结果 (步长为2-2，2-5，2-8，2-11)

由图2可以得到:时间步长h依次缩小8倍，显式Euler方法得到的数值解越来越接近解析解.还可以看到t的范围在0到0.75之间时，模拟出来的数值解与解析解误差是很大的，但是t的范围在0.75到1时，解析解与数值解相比于之前较为接近，误差越小.

通过计算可以得到：步长为2-2，2-5，2-8，2-11时，平均绝对误差分别为0.0181，0.0144，0.0128，0.0103，这说明随着步长逐渐减小，得出的数值解与解析解的误差越来越小，逼近效果也渐渐变好.

对于方程(6)，取λ=0.5，μ=1，X0=1，取T=1,h=2-8模拟数值解，分别对显式Euler方法和梯形Euler方法得到的数值解与方程的解析解进行对比，结果如图3和图4所示.

由图3和图4可以发现，显式Euler方法与梯形Euler方法相比，用梯形Euler方法得到的数值解更加接近解析解，且用梯形Euler方法模拟数值解时，t的范围在0.7至1之间模拟效果最好，数值解与解析解差距最小.另外显式Euler方法与梯形Euler方法的误差分别是0.4715和0.0406，表明梯形Euler方法比显式Euler方法得到的数值解更加精确.

图3 显式Euler数值解与解析解 图4 梯形Euler数值解与解析解

令λ=1，μ=0.3，X0=2，N=2-11，取时间步长h分别为2-2，2-5，2-8，2-11，模拟方程(6)的数值解，结果如图5所示.

可以看出，随着步长从2-2逐渐减小到2-11，数值解与解析解的误差也越来越小.另外，t在0.6至1之间时，数值解与解析解的拟合效果最好.

下面将对Milstein方法与Euler方法进行比较.对于随机微分方程(6)，令λ=2，μ=1，X0=1，分别计算步长为2-3，2-6，2-9，2-12时，随机微分方程解析解、Euler方法模拟数值解以及Milstein方法模拟数值解的运算时间，统计结果如表1所示；而Euler方法、Milstein方法的平均绝对误差，计算结果如表2所示.

由表1可以看出，时间步长越大，运算时间越短，但是模拟的结果越不精确.同时由表2可以看出：随着步长逐渐缩小，Euler方法和Milstein方法的平均绝对误差也慢慢减小，且Milstein方法的平均绝对误差比Euler方法的平均误差要小，说明了Milstein方法的数值解更加精确.

3 总 结

本文对齐次线性随机微分方程数值求解的Euler方法与Milstein方法进行研究分析，我们发现，显式Euler方法与Milstein方法都能够准确模拟出随机微分方程的解，而 Milstein方法得出的数值解的精度最高，梯形Euler方法精度次之，显式Euler方法精度最低；通过计算能够得出显式Euler方法与Milstein方法的运算时间，且运算时间越长，得到的数值解越精确.

图5 显式Milstein法数值运算结果 (步长为2-2，2-5，2-8，2-11)

表1 运算时间计算结果

表2 Euler方法与Milstein方法的平均绝对误差