饱和非线性超晶格中带隙孤子的特性研究

黎 磊，胡佐富，陈文洁，陈彦彰，钟 超

饱和非线性超晶格中带隙孤子的特性研究

*黎 磊，胡佐富，陈文洁，陈彦彰，钟 超

（井冈山大学数理学院，江西，吉安 343009）

利用光谱重构法求解了聚焦饱和非线性超晶格半无穷带隙中的基模孤子，并研究了饱和程度和超晶格势场的相对强度对孤子的功率、稳定性的影响。研究结果表明：对于给定相对强度的超晶格势场，当饱和程度较低时，孤子在高功率区域不稳定，并且孤子的稳定范围随着饱和程度的增大而变宽；当饱和程度较高时，孤子功率随传播常数增大快速增大，但孤子是稳定的。此外，对于给定的低饱和程度，孤子的稳定范围随着超晶格中低频格子相对强度的增大而变宽。

带隙孤子；超晶格；饱和非线性；光谱重构

0 引言

光在非线性介质中传输时，当非线性效应导致的会聚效果和光束衍射效应导致的发散效果相平衡时，光束在介质中会以不变的宽度、强度传输，这类光束被称为空间光孤子。早期的空间光孤子研究主要集中在均匀介质中，近些年，随着光学诱导技术的不断提高，人们发现引入外势可以给空间光孤子带来了很多新的特性。因此，各种势场调节下的空间孤子研究引起了研究人员极大的关注，如：Bessel势场[1]、Mathieu格子[2]、高斯势[3]、啁啾势场[4]、周期晶格势[5]等。而且当对光学介质的折射率进行周期调制时会形成光学格子结构，这种周期格子在物理上的特点是存在布洛赫带隙结构，所谓的带隙孤子就是局域在带隙中的非线性模。

带隙孤子可以存在于多种非线性系统中，通过不同的非线性响应可以调节带隙孤子的特性，如：非局域非线性[6]，饱和非线性[7]，三五次竞争非线性[8]等。再者，带隙孤子的种类繁多，例如：将带隙中不同的非线性模式耦合在一起可以形成矢量带隙孤子[9]；在二维的晶格中，存在带隙涡旋孤子[10]；在周期系统表面可以局域表面带隙孤子[11]；PT对称晶格中存在稳定的复数带隙孤子[12]；光晶格中的带隙暗孤子[13]也有相应的报道。近期，带隙孤子的研究拓展到了分数维[14-15]。带隙孤子具有均匀介质无法比拟的特性，不仅在光学系统，在玻色-爱因斯坦凝聚[16]等其他非线性周期系统中也被广泛研究。

带隙孤子的类型和其对应的非线性传播常数在带隙中的位置以及非线性的类型密切相关。例如：对于聚焦非线性周期系统，基模孤子存在于半无穷带隙中，亚基模孤子存在于第一带隙中；对于散焦非线性周期系统，基模孤子主要存在于第一带隙中，亚基模孤子存在于第二带隙中。改变光学格子的结构和参数可以调节带隙结构，从而控制不同类型的带隙孤子的形成、功率以及稳定性等性质。比如：用两个不同周期的格子叠加可以形成超晶格结构[17]。超晶格多了一个调控格子相对强度的自由度，而饱和非线性在调制孤子的功率和稳定方面有着独到的优势[18]。因此，将两者结合起来，研究超晶格势场和饱和非线性效应共同调制下的带隙孤子具有重要意义。

本文详细研究了饱和聚焦非线性下光学超晶格半无穷带隙中的基模孤子。通过光谱重构法[19-20]求出孤子解，然后着重探讨了非线性的饱和程度和超晶格的相对强度对孤子稳定性的影响，发现增大饱和程度以及超晶格中低频格子的相对强度有利于孤子的稳定。

1 理论模型

基于聚焦饱和非线性介质的线性光学格子中的光孤子可以用下面的归一化的非线性薛定谔方程来描述：

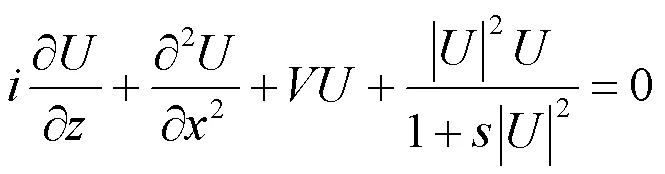
其中，是光场，，分别是横向坐标和纵向坐标，是晶格势场，代表线性折射率的调制。我们考虑由两个不同周期格子叠加形成的超晶格势场为：

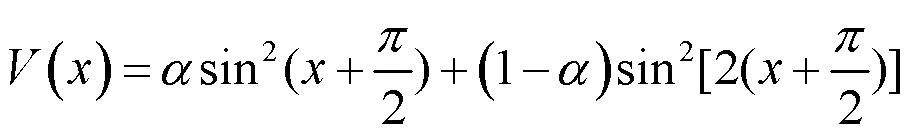
公式中是超晶格势场的调制参数，可以用来调节低频和高频格子的相对强度。图1 (a)为=0.4时的超晶格势场。

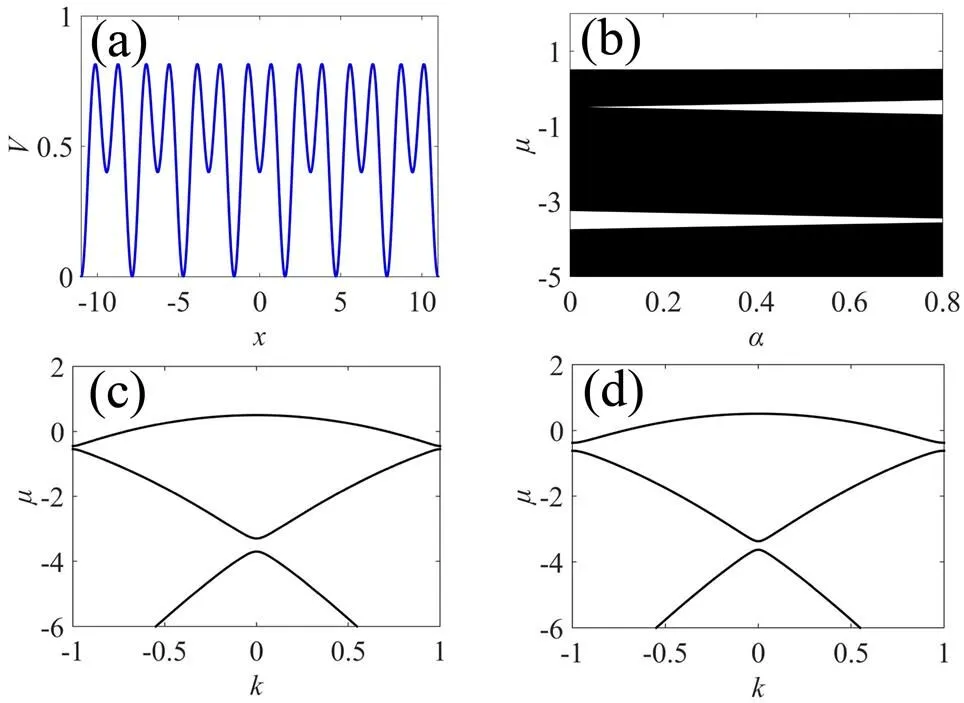
(a) 超晶格势场，α = 0.4；(b)带隙结构随α的变化关系，能带曲线；(c) α = 0.2；(d) α = 0.5

为了计算带隙结构，考虑非线性薛定谔方程的线性部分：

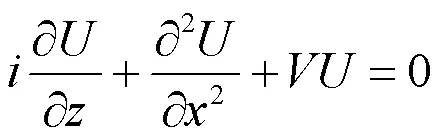
根据Bloch理论，方程(3)的本征函数可以写成=Fexp()，是Bloch波矢，F是和势场同周期的周期函数。将Bloch解代入方程(3)，可以得到本征方程：

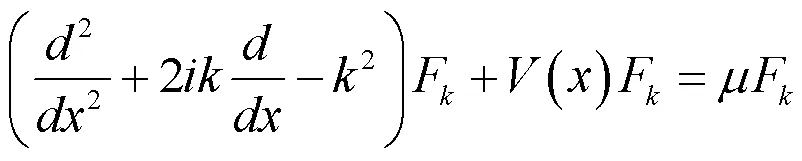
采用平面波展开法求解方程(4)，可得该系统的带隙结构随超晶格势场的调制参数的变化关系，如图1(b)所示。从图中可知，随着的增大，第一带隙逐渐变宽，而第二带隙则逐渐变窄。但是对半无穷带隙范围的影响很小，图1(c)、1(d)分别为= 0.2，= 0.5时的Bloch能带图。这里仅讨论半无穷带隙中的孤子。

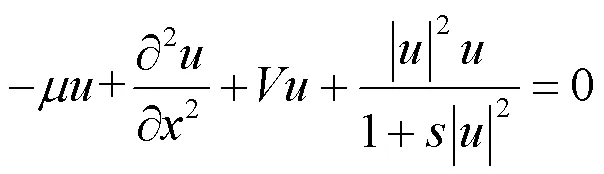
对(5)式中的线性部分应用傅里叶变换，然后再进行傅里叶逆变换，得到：

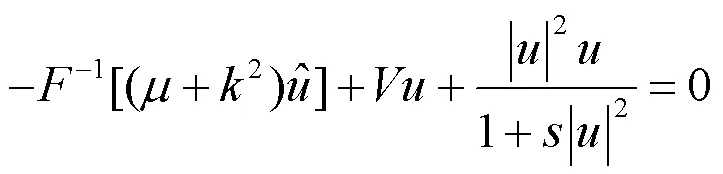
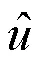
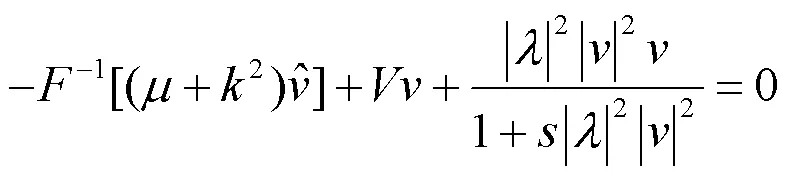
去分母后得到：

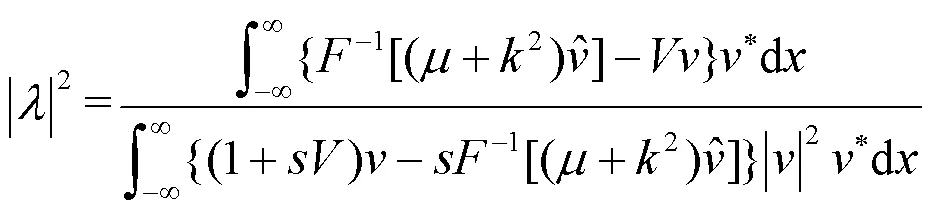
通过方程(7)，可以表示为：

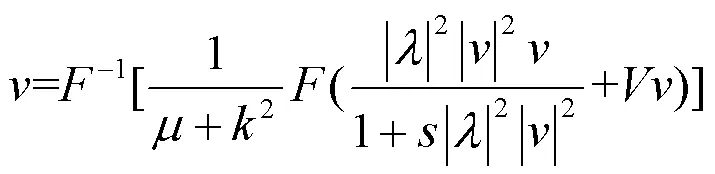
其中，代表傅里叶变换。于是，得到孤子解的迭代公式为：

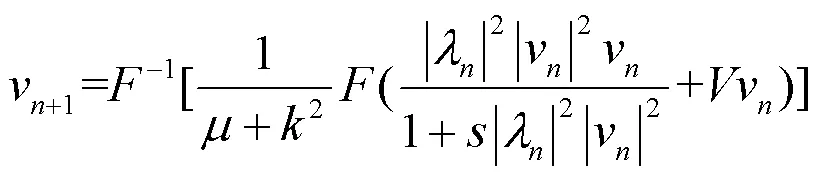
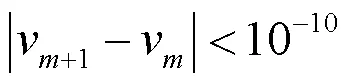
为了分析孤子的稳定性，我们在求出的孤子解中加入微扰：

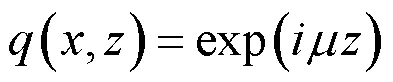
代入方程(1)，得到本征方程为：

数值求解方程(13)可以得到微扰增长率e()，当其最大值等于0时，孤子是线性稳定的，否则是线性不稳定的。

2 数值模拟和讨论

接下来，我们数值讨论饱和参数和超晶格的调制参数对孤子特性的影响。首先，固定= 0.2，计算三种不同的饱和参数= 0.1,= 0.2,= 0.3下孤子的功率随着传播常数的变化关系，结果如图2(a)所示。我们发现孤子的功率随着传播常数的增大而增大，并且饱和参数越大，孤子的功率上升的越快。这从物理上很容易理解，因为传播常数就是各种效应引起的总相移（这里包含超晶格势场调制效应以及饱和非线性效应），对于聚焦饱和非线性，功率越大，则非线性效应引起的非线性相移越大。另外，在较大的饱和参数下，非线性效应的饱和程度越高，这种情况下当功率达到一定程度的时候，如果继续增大功率，相移也会呈现饱和的效果，即的增加趋于平缓。反应在-曲线上，体现的是越大，曲线越陡，即功率随传播常数变化的越快。另外，同一个传播常数下，越大，孤子功率越高。物理上，饱和程度越大，则非线性效应越弱，所以需要更大的功率来增大非线性相移使总相移即传播常数相等。然后，我们对孤子解进行线性稳定性分析，并在-曲线中分别用实线和虚线来区分孤子的稳定区域和不稳定区域。计算发现在较弱的饱和非线性程度下，孤子在高功率区域不稳定。并且孤子的稳定范围随着饱和参数的增大而变宽，当饱和程度较高时，孤子都是稳定的，也就是说饱和非线性效应有利于孤子的稳定。

(a) α=0.2 (b) α=0.3,s=0.1 (c) α =0.4,s=0.1 (d) α=0.5,s=0.1

我们通过同一个传播常数= 2.5时两个不同饱和参数= 0.2，= 0.3下的孤子来举例说明。图3(a)，3(b)分别给出了= 0.2和= 0.3时的基模孤子解，对应的线性稳定谱分别见图3(c)，3(d)，对比两图可知，当=0.2时，微扰增长率e()大于0，说明此时孤子是不稳定的，但是当=0.3时，其微扰增长率e()等于0，说明此时孤子是稳定的。为了进一步验证孤子的稳定性，我们在孤子解上加上10%孤子幅度的白噪声，然后采用对称分步傅里叶算法模拟孤子的传输。当=0.2时，图3(e)中的传输模拟发现孤子传输很短的距离后波形就发生了形变，验证了此时的孤子是不稳定的。当=0.3时，图3(f)中的传输模拟发现孤子传输很长的距离仍然维持原有的波形，此时的孤子是稳定的。传输模拟和线性稳定性分析的结果符合的很好。

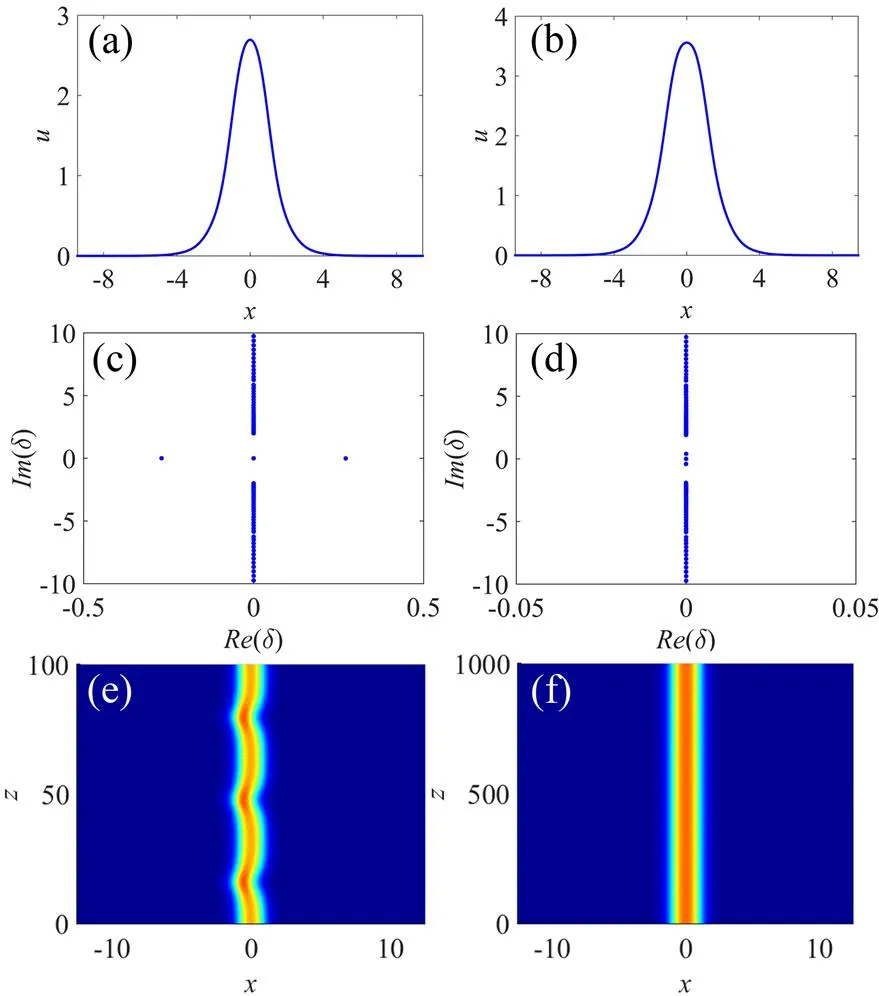
(a)(c)(e) s=0.2; (b)(d)(f) s = 0.3, α = 0.2, μ= 0.5

接下来，我们固定饱和参数=0.1, 改变超晶格调制参数。为了进一步计算了三种不同的调制参数=0.3,=0.4,=0.5下孤子的功率和稳定性随着传播常数的变化关系，结果分别如图2(b)、2(c)、2(d)所示。稳定性分析表明：当=0.2时，孤子在传播常数0.6 ～ 1.43范围内是稳定的；当= 0.3时，孤子的稳定范围拓展到0.6 ～ 1.89；当= 0.4时，孤子的稳定区域为0.6 ～ 2.63；当= 0.5时，孤子在0.6 ～ 4.46范围内稳定。也就是说，孤子的稳定范围随着超晶格调制参数的增大而变宽。举例来说，对于= 1.5，图4(a)、4(b)分别是= 0.2，= 0.3时的孤子解，两个孤子的外形轮廓差不多，功率也相差不大，物理上，由图1(b)可知，改变超晶格的调制参数，能带结构并没有明显移动，尤其是半无穷带隙，也就是说超晶格的相对强度对总相移的影响很小，所以对于同一个传播常数（总相移相同），由饱和非线性效应引起的非线性相移也应该相差不大，故而在和固定的情况下，不同下的孤子功率相差不大。但是孤子的传输模拟表明：当=0.2时，孤子是不稳定的，见图4(c)，而当= 0.3时，孤子是稳定的，见图4(d)。对于另一个例子= 3，孤子在= 0.2，= 0.3，= 0.4时都是不稳定的，但是= 0.5时，孤子是稳定的。我们分别给出了= 0.4，= 0.5时的孤子解，见图5(a)、5(b)；相应的传输模拟见图5(c)、5(d)，结果进一步证实了增大超晶格中低频格子的相对强度（即调制参数）有利于孤子的稳定。

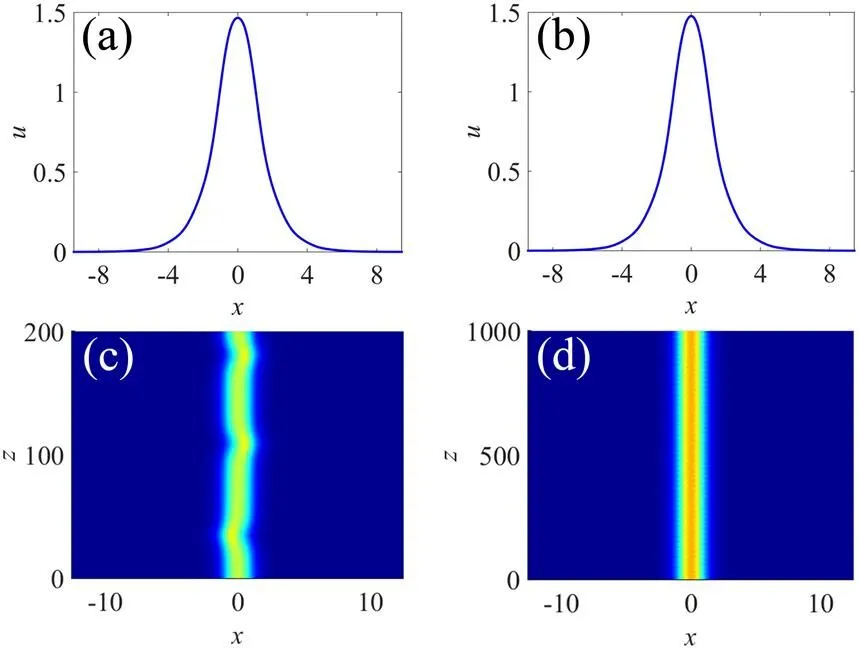
(a)(c)α = 0.2；(b)(d)α = 0.3，s = 0.1, μ = 1.5

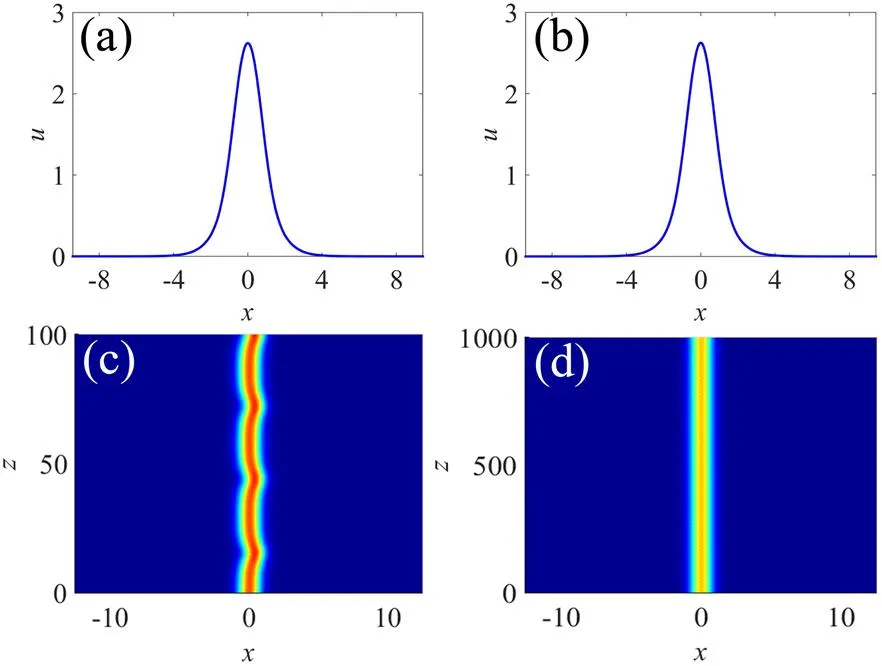
(a)(c)α = 0.4；(b)(d)α = 0.5，s = 0.1, μ = 3

3 结论

我们研究了聚焦饱和非线性超晶格半无穷带隙中的基模孤子，讨论了非线性的饱和程度和超晶格的相对强度对孤子的功率、稳定性的影响。研究发现，对于固定相对强度的超晶格势场，孤子的稳定范围随着饱和程度的增大而变宽，当饱和程度较低时，孤子在高功率区域不稳定；当饱和程度较高时，孤子功率随传播常数增长很快，但孤子是稳定的。另外，对于给定的低饱和程度，超晶格中低频格子的相对强度越大，孤子的稳定范围越宽。综上，增大非线性的饱和程度以及超晶格中低频格子的相对强度有利于孤子的稳定。

[1] Ruelas A, Lopez-Aguayo S, Gutierrez-Vega J C. Soliton dynamics in modulated bessel photonic lattices [J]. Phys.Rev.A, 2010, 82: 063808.

[2] Kartashov Y V, Egorov A A, Vysloukh V A, et al. Shaping soliton properties in Mathieu lattices [J]. Opt. Lett., 2006, 31(2): 238-240.

[3] Zheng Y, Meng Y J, Liu Y W. Solitons in gaussian potential with spatially modulated nonlinearity [J]. Opt. Commun., 2014, 315: 63-68.

[4] Kartashov Y V, Vysloukh V A, Torner L. Soliton control in chirped photonic lattices [J]. J. Opt. Soc. Am. B, 2005, 22(7): 1356-1359.

[5] Efremidis N K, Hudock J, Christodoulides D N, et al. Two-dimensional optical lattice solitons [J]. Phys.Rev.Lett., 2003, 91(21): 213906.

[6] Xu Z Y, Kartashov Y V, Torner L. Soliton mobility in nonlocal optical lattices [J]. Phys.Rev.Lett., 2005, 95: 113901.

[7] Yang J K, Makasyuk I, Bezryadina A, et al. Dipole and quadrupole solitons in optically induced two-dimensional photonic lattices: theory and experiment [J]. Stud. Appl. Math., 2004, 113(4): 389-412.

[8] Wang J D, Ye F W, Dong L W, et al. Lattice solitons supported by competing cubic-quintic nonlinearity [J]. Phys. Lett. A, 2005, 339(1-2): 74-82.

[9] Kartashov Y V, Zelenina A S, Vysloukh V A, et al. Stabilization of vector solitons in optical lattices [J]. Phys.Rev.E, 2004, 70: 066623.

[10] Wang J D, Ji H, Liu P S. Vortex solitons in the semi-infinite gap of optically induced periodic lattices [J]. Chin.Phys.B, 2013, 22(4):044207.

[11] Kartashov Y V, Vysloukh V A, Torner L. Surface gap solitons [J]. Phys.Rev.Lett., 2006, 96: 073901.

[12] Musslimani Z H, Makris K G, El-Ganainy R, et al. Optical solitons in PT periodic potentials [J]. Phys.Rev.Lett., 2008, 100 (3): 030402.

[13] Dong R, Rüter C E, Song D H, et al. Formation of higher-band dark gap solitons in one dimensional waveguide arrays [J].Opt. Express, 2010, 18(26):27493- 27498.

[14] Huang C M, Dong L W. Gap solitons in the nonlinear fractional Schrödinger equation with an optical lattice [J]. Opt. Lett., 2016, 41(24): 5636-5639.

[15] Li L, Li H G, Ruan W, et al. Gap solitons in parity-time-symmetric lattices with fractional-order diffraction [J]. J. Opt. Soc. Am. B, 2020, 37(2): 488-494.

[16] Mayteevarunyoo T, Malomed B A. Stability limits for gap solitons in a Bose-Einstein condensate trapped in a time-modulated optical lattice [J]. Phys.Rev.A, 2006,74: 033616.

[17] Louis P J Y, Ostrovskaya E A, Kivshar Y S. Dispersion control for matter waves and gap solitons in optical superlattices [J]. Phys.Rev.A, 2005, 71: 023612.

[18] Li L, Li H G, Lai T S. Defect solitons in parity-time symmetric superlattices with focusing saturable nonlinearity [J]. Opt. Commun., 2015, 349: 171-179.

[19] Ablowitz M J, Musslimani Z H. Spectral renormalization method for computing self-localized solutions to nonlinear systems [J]. Opt. Lett.,2005, 30(16): 2140-2142.

[20] 郑睿,高星辉,曹伟文,等.光谱重置法在非局域空间光孤子研究中的应用[J].物理学报,2010,59(2):1063-1068.

PROPERTIES OF GAP SOLITONS IN SUPERLATTICES WITH SATURABLE NONLINEARITY

*LI Lei, HU Zuo-fu, CHEN Wen-jie, CHEN Yan-zhang, ZHONG Chao

（School of Mathematics and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China）

The fundamental solitons in the semi-infinite gap of superlattices under focusing saturable nonlinearity are solved by the spectral renormalization method. The effects of saturation degree and relative strength of superlattice potential on the power and stability of solitons are studied. The results show that for a fixed relative strength of superlattice potential, when the saturation degree is low, the solitons are unstable in the high-power region, and the stable range of the solitons becomes wider with the increase of the saturation degree. When the saturation degree is high, the soliton power grows dramatically with propagation constant, but the solitons are stable. Besides, for a given low saturation degree, the stable range of the solitons widens with an increase in the relative strength of low-frequency lattice in the superlattice.

gap soliton; superlattice; saturable nonlinearity; spectral renormalization

O437.5

A

10.3969/j.issn.1674-8085.2022.06.001

1674-8085（2022）06-0001-06

2022-03-20；

2022-04-12

国家自然科学基金项目(11764022)；江西省教育厅科技计划项目(GJJ180588)

*黎 磊(1988-)，男，江西吉安人，讲师，博士，主要从事空间光孤子研究(Email:fanrenlilei@126.com).