题源探秘 多解思维 变式拓展
——一道零点存在性问题的探究
浙江省绍兴市上虞区城南中学
方镇军
涉及函数零点的存在性问题是历年高考数学试题中的热点与难点问题之一,每年高考试卷上都有其熟悉的影子.巧妙地把函数零点与存在性这两个重点问题加以融合,创新新颖,变化多端,同时又可以很好融合其他相关的数学知识,有效考查考生的数学知识、数学思想方法与数学能力等,具有较好的高考区分度与选拔性,一直备受命题者青睐.
1 问题呈现
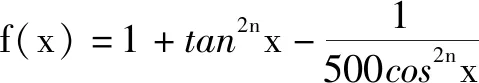
此题以函数零点的存在性为问题背景,交汇并融合三角函数、不等式、函数的最值以及函数的零点等众多知识,题目简单明了,创新新颖.抓住函数本质,利用函数零点的存在性加以突破,可以通过导数思想,换元、重要不等式等思维巧妙切入,利用导数法或重要不等式法来处理,进而得以破解.
2 问题破解
思维视角一:导数思维.

故填答案:10.
点评:根据函数的零点存在性问题对函数的解析式加以变形,等价转化并合理构造对应的函数.利用导函数的零点的确定与求解来转化与确定所构造函数的最小值,进而根据题目条件建立相应的指数不等式,结合正整数n来确定其最小值.导数法直接处理,目的明确,只是运算量大,过程繁杂.
思维视角二:换元思维.
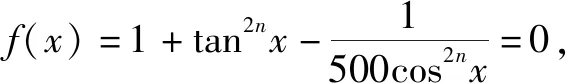
故填答案:10.
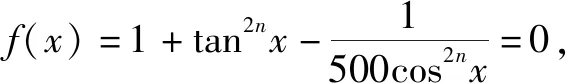
故填答案:10.

故填答案:10.
点评:根据函数解析式的特征,借助正弦换元、均值换元或正切换元等方式引入参数;结合函数的构造,通过求导,利用导数及其应用来确定函数的最小值;根据指数不等式的求解,以及正整数n来确定其最小值问题.换元是手段,简化关系式、求导是目的.不同的换元处理,有不同的解题功效.
思维视角三:重要不等式思维.
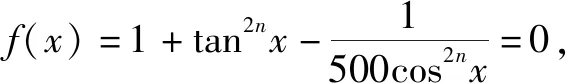
故填答案:10.
点评:根据函数的零点存在性问题加以变形,结合三角关系式的合理转化,利用权方和不等式确定三角关系式的最小值,进而根据题目条件建立相应的指数不等式,通过不等式的求解,以及正整数n来确定其最小值问题.借助权方和不等式转化确定最值是破解的关键所在,只是该不等式对大部分考生来说比较陌生,只是作为一个了解.
3 题源探秘
根据原问题的分析与破解,其实质是求解函数f(x)=sin2nx+cos2nx的最小值问题,巧妙利用函数零点的存在性以及指数不等式加以进一步地融合、提升与拓展.回归本质,探秘题源.
问题(2010年全国高中数学联赛福建省赛区预赛第7题)函数f(x)=sin2kx+cos2kx(k∈N*)的最小值为______.
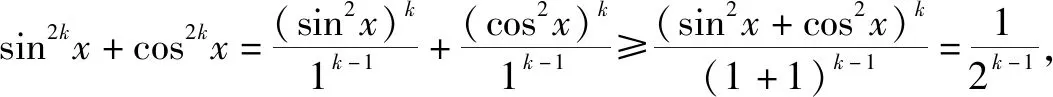
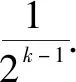
点评:对比高中数学联赛问题,破解时直接借助权方和不等式,可以更加快捷地处理该问题.而对一般考生来说,利用导数法或换元法处理也同样可以求解,这里不多赘述,可以参考原问题的解析过程求解.
4 解后反思
涉及函数零点的存在性问题是相关的数学知识、数学思想方法和数学关键能力等方面交汇与融合的一个很好场所,破解的基本思路是进行合理的等价转化,变形为相应的方程、对应的代数式、函数的解析式等,通过方程思想、代数式的不等式处理、函数的图象与性质、导数法等来分析与处理.破解此类问题要求具备比较高的化归与转化能力、逻辑推理能力等,同时对创新意识与创新应用等方面都有较高的要求.

