一类复值时滞中立型神经网络的稳定性分析

肖 瑶，段腾飞

(南京财经大学 应用数学学院，江苏 南京 210046)

近年来，由于递归神经网络在模式识别分类、信号处理、工程优化和联想记忆等领域的广泛应用，使得其稳定性等动态行为被广泛研究[1-3].在复杂系统的理论和应用中会出现复值信号的情况，而实值神经网络不能很好地解决此类问题，复值神经网络(CVNNs)[4，5]便应运而生.实际上，CVNN在某种意义上可以看作是对实值神经网络(RVNN)的扩展，其将RVNN中的状态变量、激活函数和突触强度矩阵变成了复值.因此，这种网络在许多方面比RVNN具有更复杂的特征，相应的.它能够解决许多实值神经网络无法解决的问题[6,7].例如，当一些现实中的应用包含复杂信号时，复值模型可对复杂信号的相位和振幅信息同时进行编码，以减少和简化信息处理的复杂性.因此，研究CVNN的动态行为，特别是稳定性和同步性是非常重要的.目前，对复值递归神经网络的研究已经取得了一些成果.文献[8]建立了广义离散复值神经网络模型，导出了新的检验平衡点全局指数稳定的判别条件，在实际应用中获得了更一般的收敛性结果.文献[9]使用M-矩阵和线性矩阵不等式的方法，研究了具有时滞的连续复值递归神经网络，得到了2种不同复值激活函数下全局指数稳定的判据.文献[10]通过平均脉冲增益和平均脉冲区间的概念，设计了一个合适的混合脉冲控制器来确保实现驱动-响应复值神经网络之间的指数同步.

一般来说，由于放大器的开关速度有限，而且在神经网络(NNs) 的硬件实现中，信号的传输速度有限，所以时间延迟在NNs 中是不可忽略的.由于时间延迟的存在，在NNs 中可能会出现一些动态行为，其中包括周期性振荡、不稳定、分叉等[11].基于上述原因，研究延迟NNs 的动力学特性[12-14]具有重要的理论意义和应用价值.

中立型动力系统是一种演化系统，常被用来描述当前状态的变化率取决于过去状态的变化率.中立型神经网络(NDNN)是一类涉及过去状态导数的中立型动力系统，在数学，受控约束操纵器，无损传输线，生态环境系统和控制系统等领域经常使用.与其他神经网络系统相比，中立型神经网络具有更复杂的动态特性.因此引起了许多学者的关注，特别是对NDNN 的稳定性和同步性的研究.文献[15]通过构造一个新Lyapunov-Krasovskii 泛函，研究了带有多个时变离散中立型时滞的中立型 Cohen-Grossberg 神经网络的全局指数稳定性.文献[16]给出了带有各种混合时变时滞的中立型神经网络的有限时间稳定性的一些简单新颖的充分条件.文献[17]通过Lyapunov 稳定性理论,利用了LMI分析技巧和矩阵理论，研究了具有随机扰动和Markov 切换的中立型神经网络的自适应同步，得出了具有时变时滞和随机扰动的中立型神经网络的自适应同步的判据.在各类神经网络的研究中，从数学的角度来看，最重要的问题是如何证明解的唯一平衡点的稳定性.因此，如何获得神经网络的稳定性条件已成为许多研究者关注的焦点.此外，在神经网络分析中，为神经网络提供一个理想的收敛速度也是必不可少的.因此，研究人员的主要目标是获得平衡解的指数稳定性条件[18,19].在研究稳定性问题时,Lyapunov 稳定性理论一直受到人们的关注[20].然而,Lyapunov 方法存在一些局限性.例如，它不能反映系统的瞬时性，可能对实际系统产生不好的影响，甚至不能使用.此外，分析时变系统的非对称稳定性通常具有挑战性，因为要找到具有负定导的李亚普诺夫函数是非常困难的.在现有的大多数文献中，NDNN 的稳定性研究基本上是构造Lyapunov 泛函并由线性矩阵不等式给出的，这在应用上就会比较复杂.

在大多数论文中，激活函数均是单变量的，但是复值的情况可能更加复杂，需要考虑双变量的情况.受上述讨论启发，本文的主要目的是研究具有双变量激活函数的复值时滞NDNNs 的全局指数稳定性，采用了微分代数不等式方法，给出了更加简洁的定理结论.

本文主要创新点如下:

1) 本文建立了具有双变量激活函数的复值时滞中立型神经网络模型;

2) 本文提出了微分代数不等式方法，不再需要构造Lyapunov 泛函，结果更加简便有效;

3) 本文利用全局指数自同步概念来证明全局指数稳定性，同时本文的方法也可以用来研究多种模型的同步性问题.

1 模型与预备知识

考虑如下中立型神经网络模型:

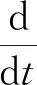
(1)

其中，z(t)=[z1(t),z2(t), …,zn(t)]T∈n为复向量值的神经元状态，C=diag{c1,c2,…,cn}，ci>0 (i=1,2,…,n)，D=[dij]n×n∈n×n表示实值的时滞连接权矩阵，A=[aij]n×n∈n×n和B=[bij]n×n∈n×n分别表示不带有和带有时滞的反馈连接权重矩阵，F(z(t))=[F1(z1(t)),F2(z2(t)), …,Fn(zn(t))]T∈n和G(z(t-τ))=[G1(z1(t-τ)),G2(z2(t-τ))， …,Gn(zn(t-τ))]T∈n分别表示无时滞和有时滞的复向量值激活函数，τ>0 表示恒定时间延迟，J=[J1,J2,…,Jn]T∈n表示恒定偏置性向量值输入.

假设1设z=α+iβ，其中α,β∈，同时Fi(zi) 以及也可以用它的实部和虚部来表示为：

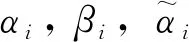
(2)

(3)

系统(3)的初始条件由下式给出:

x(s)=x0(s),s∈[t0-τ,t0],

想要运用微分代数不等式方法，还需要对系统再做近一步变换,如下所示:

(4)

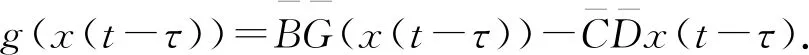
定义1若存在M≥1 以及λ>0 使得：

则系统(4)的平衡点 (y*T,x*T)T是全局指数稳定的.

注1在这里，系统(4)与系统(1)是等价的,两个系统的平衡点的性质也是完全一致的.

定义2如果存在两个常数M≥1 以及λ>0，使得：

引理1如果Q=[qij]n×n的所有非对角线元素都是非正的，则以下条件彼此等价:

1)Q是一个非奇异M-矩阵(NSMM);

4)Q的逆矩阵Q-1>0 正定.

引理2如果一个矩阵的所有元素都是非负的，我们称该矩阵为非负矩阵.设Q∈n×n为非负矩阵，则In-Q是NSMM当且仅当λmax(Q)<1.

引理3设φ,ψ:[t0-τ,+∞)→[0,+∞).φ(t) 以及ψ(t)分别是连续可微函数和连续函数，满足下述条件:

(5)

对于t≥t0，其中a1是任意常数，a2,b1,b2,c1和c2都是正实数.如果λmax(Λ)<1， 那么当t→+∞时，φ(t)→0和ψ(t)→0成立,其中

(6)

那么

(7)

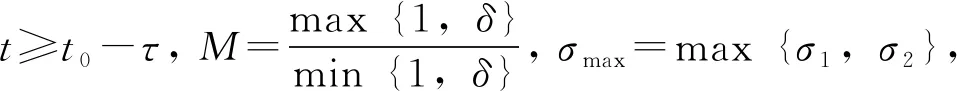
引理4[21]在下述系统中，系统平衡点的全局指数稳定性等价于其全局指数自同步:

(8)

通过引理4易得以下引理:

引理5系统(4)的全局指数稳定性等价于其全局指数自同步.

2 主要结果

令

定理1当假设1成立，令

证明根据引理5，我们只需证明系统(4)是全局指数自同步的.

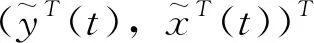
(9)

(10)

通过(8)和(9),可以得到：

(11)

同理可得:

(12)

令φ(t)=max1≤i≤2n|Yi(t)|和ψ(t)=max1≤k≤2n|Xk(t)|.对于任意固定的t>t0，有i∈{1,2,…,2n} 和k∈{1,2,…,2n}，使得φ(t)=|Yi(t)| 以及ψ(t)=|Xk(t)|.

所以有：

(13)

以及

(14)

通过(13)和(14),可以得到:

(15)

利用引理2可以推出,当λmax(Λ)<1时，Im-Λ是一个NSMM.而通过引理1可知，存在一个常数δ>0 使得：

(16)

(17)

根据(17),很容易得到如下矩阵范数不等式：

(18)

这就意味着,系统(4)是全局指数自同步的.从而利用引理5,系统(4)是全局指数稳定的.

3 数值仿真

在本章节,将给出一个数值算例来验证上述结论的正确性.

例 考虑如下二维复值NDNN神经网络模型：

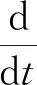
(19)

其中

那么，通过文章的定义，可以得到

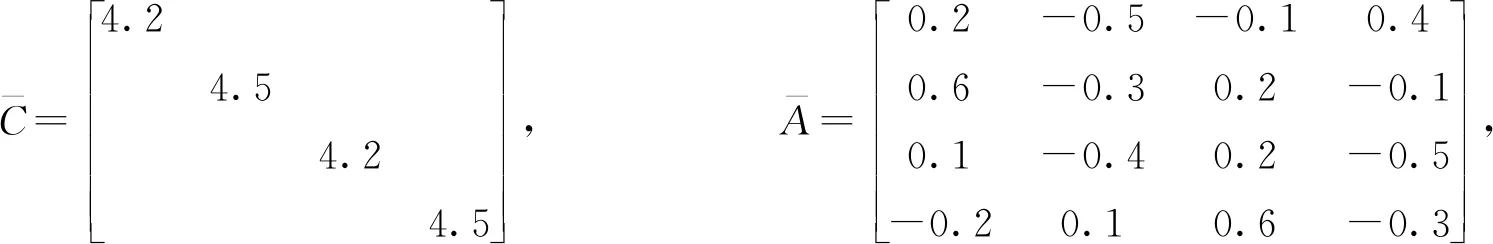
通过计算，可以得到以下数值：

取κ=3.83，此时 0<κ≤3.833 4，则有

计算得，λmax(Λ)=0.876 4<1，故根据定理1可知系统是全局指数稳定的.

图1、图2、图3、图4分别给出了系统的解在以下10种初始状态下的动态曲线.初值1：z1(t)=2.5-2.2i，z2(t)=-0.9+3i; 初值2：z1(t)=1.4+1.6i,z2(t)=3.6-1.4i; 初值3：z1(t)=-3.3-0.7i,z2(t)=4.5+2.8i; 初值4：z1(t)=-0.2+3.4i,z2(t)=2.1-3.5i;初值5：z1(t)=3.6+2.8i,z2(t)=-5.4-0.2i; 初值6：z1(t)=0.7-3.1i,z2(t)=-2.3+2.4i; 初值7：z1(t)=4.1-4.4i,z2(t)=0.3+1.5i; 初值8：z1(t)=-1.9+4.7i,z2(t)=-3.6-2.6i;初值9：z1(t)=-2.7-1.8i,z2(t)=1.4+4.1i;初值10：z1(t)=5.1+5.2i，z2(t)=-5.3-5.4i.

图1 系统状态向量z(t)的实部第1分量α1(t)的轨迹

图2 系统状态向量z(t)的实部第2分量α2(t)的轨迹

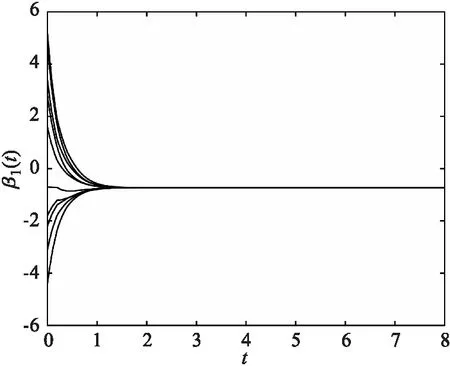
图3 系统状态向量z(t)的虚部第1分量β1(t) 的轨迹

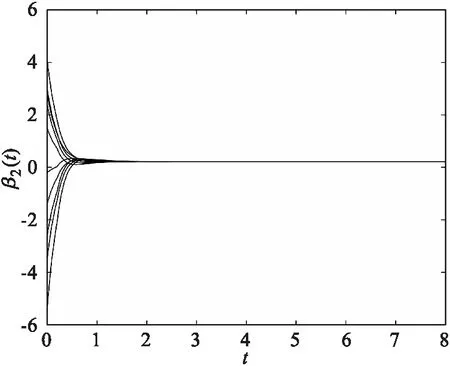
图4 系统状态向量z(t)的虚部第2分量β2(t) 的轨迹

4 结论

本文针对复值时滞NDNN模型，利用较为新颖的微分代数不等式方法，不再需要构造Lyapunov函数，给出了更加简洁的全局指数稳定性条件，所得的结论更加广泛适用.最后,本文提供了一个数值算例证明了结论的有效性.本文提出的方法还可以用于解决多种神经网络动力学问题，如DDANNs，NDNNs的多稳定性、多同步、周期振荡、分岔和混沌,以及各种控制问题.