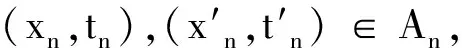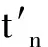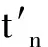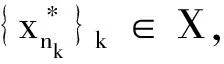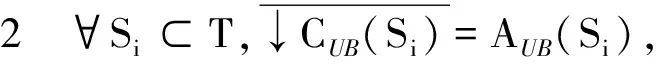广义模糊函数空间的稠密性和闭包表示
杨寒彪,林文辉,文钊颖,金迎迎,杨 琳
(1 五邑大学 数学与计算科学学院,广东 江门 529020;2 广州番禺职业技术学院 公共课教学部,广东 广州 529000;3 江门职业技术学院 化学材料系,广东 江门 529000)
令(P,≤)是一个偏序集,d是P上的一个度量。若(P,≤,d)由d导出的拓扑与(P,≤)的拓扑一致,则称(P,≤,d)是一个偏序度量空间。
对于一个紧度量空间(X,d),以及一个紧偏序度量空间(P,≤,d),令C(X,P)是所有从X到P的连续函数所构成的集合。本文认为连续函数f∈C(X,P)是一种广义的模糊函数。∀f∈C(X,P),令
↓f={(x,p)∈X×P:p≤f(x)},
称为f的超图。↓f是X×P里的闭集。令Cld(X×P)是X×P所有带有Hausdorff度量非空闭集构成的一个族,则∀A、B∈Cld(X×P),
dH(A,B)=min{δ:A⊂Bd(B,δ),
B⊂Bd(A,δ)}。
其中d((x,p),(x′,p′))=max{d(x,p),d(x′,p′)。因此,(Cld(X×P),dH)是一个紧度量空间。∀A⊂C(X,P),
↓A={↓f:f∈A}
是(Cld(X×P),dH)的一个子空间,空间↓A可以被视为一个函数空间。更一般地,对于一个拓扑空间X(不必是紧的或可度量的)和一个拓扑偏序集P,假定T是Cld(X×P)的一个拓扑以及A是从X到P所有映射(不需要一定是连续的)的集合的一个子集,其中∀f∈A,↓f∈Cld(X×P)。因此,作为(Cld(X×P),T)的一个子空间,我们能得到一个函数空间↓AT,即本文中的广义模糊函数空间。
文献[1-18]都讨论过空间↓AT。特别地,文献[8]给出了带有Fell拓扑的所有连续函数↓CF(X,R)可度量化的充要条件,其中R是带有通常拓扑和序的实数集。此外,许多研究为了确定这些空间的拓扑结构,使用了无限维拓扑作为工具。例如,著名的Curtis-Schori-West超空间定理指出:↓USCdH(X,{0,1}){0}同胚于希尔伯特立方体Q=[-1,1]ω(记作↓USCdH(X,{0,1}){0}≈Q)当且仅当X是Peano连续统,其中{0,1}是带有离散拓扑的两点集且0≤1,USC(X,{0,1})是所有X到{0,1}的上半连续函数集合,0是值域恒为0的函数[4,11]。Sakai等[10]证明了↓USCF(X,{0,1})≈Q当且仅当X是一个局部紧、局部连通以及没有紧分量的一个可分可度量空间。文献[19-27]给出了对所有可度量函数空间↓CF(X,I),其中X是可度量的,I=[0,1]使用通常的拓扑和序。具体结论是:对一个可度量空间X,带有Fell拓扑的函数空间↓CF(X,I)可度量当且仅当X是一个局部紧可分可度量空间。此外,还有以下对同胚:
(↓USCF(X,I),↓CF(X,I))≈
其中:X0是X里所有离散点的集合;Σ={(xn∈Q):sup|xn|<1};c0={(xn∈Σ):limxn=0}。文献[18,20,23-24]证明若X是一个k空间且↓C(X,I)是可度量的,则
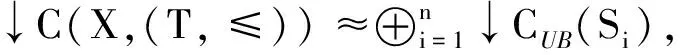
↓CUB(Si)={↓f∈C(X×T):maxf(X)∈
Si{vi}}。
此外,所有↓CUB(Si)都是可缩空间。
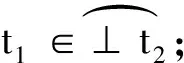

显然,⊥是(T,≼)的最小元同时是(T,≤)的最大元,∀t1、t2∈T有t1≼t2当且仅当t2≤t1,令除⊥之外的其他端点为(T,≤)的最小元。
树突(dendrite)是一个不包含简单闭曲线的Peano连续统。不同于树,树突在每一个顶点上可以有可数条边。文献[17]证明了如下结果:令X是只含有限个孤立点的有限紧可数空间,Y是一个有T上端点v的树突。对于偏序≼,有如下对同胚:
(Q,c0),

本文中,广义模糊函数空间↓C(X,(T,≤))和一般的模糊函数空间↓C(X,I)有很大区别。虽然值域都是紧的,但广义模糊函数空间的值域为有限树时,其上赋予的是偏序;而I=[0,1]的自然序显然是全序。这给拓扑性质带来很大变化,甚至有限树的不同偏序方向≤和≼都会对拓扑性质带来影响。例如,由文献[24]知,实际上↓C(X,(T,≤))是不连通的,而↓C(X,(Y,≼))≈c0是连通的。
令E是(T,≤)的边,其中E的上顶点vE在(T,≤)中。令
本文中所有枝S均如上定义。因此,视有限树(T,≤)为以上定义的枝,并且这些枝的交为空,其中一个包含最大元⊥的枝等距同构于[0,1],其他枝等距同构于[0,1)。
2 定义和预备知识
本文中,X=[0,1]=I,T=(T,≤)是有限树,顶点为k阶意味着这个顶点与k个枝相交。每一个T中每一个非端点的顶点的阶都大于等于3。把↓C(X,(T,≤))写作↓C(X,T)。记|A|为集合A的基数,|AS|为其中枝的个数,由于本文讨论的是有限树,因此|AS|有限。
我们定义一些本文所需的概念。
定义1∀A∈Cld(X×T),定义一个集值函数A:X→Cld*(T),
A(x)={t∈T:(x,t)∈A}∈Cld*(T),
其中Cld*(T)=Cld(T)∪{∅}。∀A⊂T,若∃a∈A使得a等于A的上确界∨A,把a称作A的最大元,并记作maxA。令a(x)是A(x)的最大元。当A⊂X×T,则maxA=maxp(A),其中p:X×T→T为投影函数。
定义2V(A)为A⊂T中所有的顶点,Sv为T内所有以v为上顶点的枝构成的族,Vv是Sv内所有枝的下顶点构成的集合。对T内的顶点v,u∈Vv,令T[v,u]=[u,v]∪↓u。
对任意T上的枝Si,i≤|TS|,令Si的上顶点为vi,利用以上定义可以定义本文中非常重要的几个闭集族。
定义3A={A∈Cld(X×T):∀x∈X,A(x)≠∅,A(x)存在唯一的最大元a(x),当a(x)不是顶点时,A(x)=↓a(x);当a(x)是顶点时,A(x)=↓a(x)或对某个u∈Va(x),有A(x)=T[a(x),u]}。
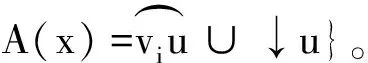
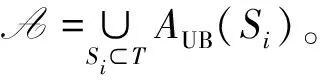
由文献[27]中的引理7,对任意连通紧集A⊂T,maxA存在。特别地,∀f∈C(X,T),maxf(X)存在。
实际上,由定理2的闭包表示,A(x)最大元a(x)存在性和maxA存在性不证自明。
注1在A的定义中,条件“对某个u∈Va(x),A(x)=T[a(x),u]”是必需的。举例,令X=I,T={0}×I∪[-1,1]×{0},端点t=(0,1)是T的最大元,t1=(-1,0)和t2=(1,0)是T的最小元。定义X×T中的闭集A如下:
A={0}×([-1,0]×{0})∪{(x,(t,0))|
x∈(0,1],t≤cosx-1}⊂
X×([-1,0]×{0})。
∀n>2,n∈N,令fn:X→[1,0]×{0}T,映射定义如下:
因此,↓fn(x)X×([1,0]×{0}),↓fn∈↓C(X,T),以及当n→∞时,函数列(↓fn)n∈N→A∈Cld(X×T)。然而,有A∈A。
我们定义如下关于端点的概念。
定义4∀A⊂(T,≤),定义
M(A)={m∈T:m是T的最小元且存在某个
a∈A使得m≤a}。
显然,∀m1、m2∈M(T,≤),m1与m2不可比较。
由文献[27]中的引理2,有如下引理。
引理1对有限树T,以及前文定义的度量d和偏序≤,⊥是其最大元,有如下结果。
1)(T,≤)是一拓扑上半格,即∀t1、t2∈T,上确界t1∨t2存在,且上确界函数∨:T×T→T是连续的。此外,对每个非空A⊂T,上确界∨A存在。
2)∀t1、t2、s1、s2∈T,d(t1∨t2,s1∨s2)≤max{d(t1∨t2),d(s1∨s2)}。

5)∀a、b、c∈T,若a 6)∀a、b∈T,a,b是可比较的,当且仅当↓a∩↓b≠∅当且仅当M(a)∩M(b)≠∅。 7)∀t∈↓t1和t′∈↓t2,若t1、t2在T中是不可比较的,则t、t′不可比较。 引理2取v∈V(T),ti∈T[v,ui],其中i=1,2,ui∈Vv,u1≠u2,则t1∨t2=v。 证明取任意的t 容易得到如下引理。 引理3若t1、t2∈T不可比较,则t1∨t2是T上的一个顶点。若t1、t2∈T可比较,则t1∨t2=t1或t1∨t2=t2。 引理4∀A∈A,v∈V(T),令Ak=A∩[X×T[v,uk]],其中u1、u2∈Vv,k=1,2。令p:X×T→X是投影映射。若∀x∈X都有a(x) 证明假定∃(x,t1)∈A1,(x,t2)∈A2,这里t1∈T[v,u1],t2∈T[v,u2]。由引理2,显然v=t1∨t2。由A的定义知(x,v)∈A,导出矛盾。 引理5∀A∈A,(x,t)、(x′,t′)∈A,其中x Ak={(y,t)|y∈[x,x′],t≤a(y),a(y)∈ T[v,uk]},其中{u1,u2,…,un}=V。 由于∀y∈[x,x′],a(y)≠v,对1≤k≠k′≤n。令 A′={(y,t):y∈[x,x′],t∈A(y), a(y)和v不可比较}= A|[x,x′]={(y,t):y∈[x,x′],t∈A(y)}= A′∪A1∪A2∪…∪Ak…∪An。 令投影函数p:X×T→X使得p(A|[x,x′])=[x,x′]。由引理4,∀1≤k≠k′≤n,p(A′)∩p(Ak)=∅,p(Ak)∩p(Ak′)=∅。此外,{p(A′),p(A1),p(A2),…,p(An)}是一族闭集,其中有至少2个集合是非空的,p(A′)∪p(A1)∪p(A2)∪…∪p(An)=[x,x′]=p(A|[x,x′])是连通的。矛盾。 由引理1的6)、引理5,得到定理1。 定理1对任意T上的枝Si,广义模糊函数子空间↓CUB(Si)在闭集族AUB(Si)上稠密,其中i≤|TS|。 {x(a,s)|(a,s)∈F}∪{0,1}= 记Si的上顶点为v′,maxA=a,取(x′,a(x′))=(x′,a)∈A,有以下两种情况。 这个新的有限序列{(xi,ti)}0≤i≤n有 (1) 若ti和ti+1不可比较,令vi=ti∨ti+1。 由公式(1)有dH(A,↓f)<ε。 由定理1,得到引理6。 证明注意到M(u)是有限集合,由A的定义,∃t∈M(u),使得对无穷多个n,有t∈An(xn)。同样地,∃t′∈M(u′),使得对无穷多个n,有t′∈An(xn)。因此,t∨t′=u∨u′=v。不失一般性,假定对所有奇数有t∈An(xn),对所有偶数有t′∈An(xn)。 (2) 由引理6,易得如下引理。 引理7∀A∈A,v∈V(T),u、u′是Vv中2个不同的顶点,t、t′∈T,x≤x′∈X。如果A(x)⊃↓t,t∈T[v,u],A(x′)⊃↓t′,t′∈T[v,u′],其中t∨t′=v,t和t′都不是顶点,则∃x*∈[x,x′],使得↓v⊂A(x*)。 由文献[28],有如下引理。 引理8对任意紧连通序列(An)n∈N∈Cld(X×T),当n→∞时,An→A,A是连通的。 由文献[27]中的引理7,有如下引理。 引理9对任意紧连通集合A⊂T,maxA存在。特别地,∀f∈C(X,T),maxf(X)存在。 为证A(X)有最大值,需要以下引理。 引理10对收敛列(An)n∈N∈A,若当n→∞,An→A∈Cld(X×T),则∀x∈X,A(x)≠∅。 证明∀x∈X和n∈N,取tn∈An(x)≠∅。由于T是紧的,可以取子列{tnk}在k→∞时收敛于某个t∈T。由于当n→∞时,dH(An,A)→0,则当k→∞, dH((x,t),Ank)≤d((x,t),(x,tnk))= d(t,tnk)→0, 由于A和Ank都是紧集,(x,t)∈A,因此A(x)≠∅。 下面的引理可以提供连通性方面的证明工具。 引理11令(An)n∈N是A中的收敛序列,当n→∞时,An→A∈Cld(X×T)。∀x0∈X以及任意非顶点t0∈A(x0),↓t0⊂A(x0)。 证明为了证明↓t0⊂A(x0),只需验证∀t′∈↓t0{t0},t′∈A(x0)。由于t0不是一个顶点,∃ε>0使得B(t0,ε)内没有顶点且∀t∈B(t0,ε)均有t′ 由引理1的2)及引理3、6、9、10、11可得如下引理。 引理12令(An)n∈N是A中的收敛序列,且当n→∞时,An→A∈Cld(X×T)。那么,∀x∈X,A(x)有最大元a(x)。 证明由引理10知A(x)≠∅。∀x∈X,为了证明A(x)有最大元a(x),由引理9,需要证明A(x)在T里是连通的。由引理11,只需证∀t、t′∈A(x),t∨t′∈A(x)。 以下引理揭示了An收敛和an(xn)收敛的关系。 引理13(An)n∈N∈A为一个收敛到A∈Cld(X×T)的收敛序列。对任意的收敛序列xn→x∈X,当n→∞时,an(xn)→a(x),其中an(xn)是An(xn)的最大元,a(x)是A(x)的最大元。 证明我们将证明an(xn)→a(x)。为此,对每个子列ank(xnk),因为An→A,所以存在子列anki(xnki),使得当i→∞时(xnki,anki(xnki))→(x,a*(x))。因为a*(x)∈A(x),所以a*(x)≤a(x)。另一方面,存在一个收敛序列tnki∈Anki(xnki),使得当i→∞时tnki→a(x)。因为tnki≤anki(xnki),所以a(x)≤a*(x)。因此,anki(xnki)→a*(x)=a(x)。 由引理1的6)及引理6、11、13,得到引理14。 引理14对任意T上的枝Si,对于任意一个收敛序列(An)n∈N∈AUB(Si),令A是(An)n∈N的极限,其中i≤|Ts|。∀x∈X,A(x)仅有两种情况。 情况1A(x)=↓a(x)。 情况2a(x)∈V(T)且对某个u∈Va(x)∩↓Si,A(x)=T[a(x),u]。 进一步,令vi为枝Si的上顶点,∀x∈X,则存在某个u∈Vvi∩↓Si,使得A(x)=T[Vvi,u];或者a(x)∈↓Si。 证明由引理10,当a(x)不是一个顶点时,A(x)=↓a(x);同理,当a(x)是一个3阶顶点,A(x)=↓a(x)或存在某个u∈Va(x)∩↓Si,使得A(x)=T[a(x),u];同理,当a(x)是一个4阶或者4阶以上的顶点时,A(x)=↓a(x)或对某个u∈Va(x)∩↓Si有A(x)=T[a(x),u]或对某个UVa(x)∩↓Si有其中1<|U|<|Va(x)∩↓Si|。 下面只需证明“当a(x)是一个4阶或者4阶以上的顶点时,对某个UVa(x)∩↓Si有其中1<|U|<|Va(x)∩↓Si|”这个情况不存在。假设当a(x)是一个4阶或者4阶以上的顶点,上面的情况存在。 由引理13,由于当n→∞时,An→A,所以存在收敛于x的序列(xn)⊂X,使得an(xn)→a(x)∈V(T),其中an(xn)是An(xn)的最大元。不失一般性,因为在必要时,可以选择(An)的子列,所以我们只需考虑An(xn)的3种情况。 情况A∀n,An(xn)=↓an(xn)且an(xn)≥a(x)。 情况B∀n,对某个u0∈U,An(xn)⊂T[a(x),u0]。 情况C∀n,对某个u0∈Va(x)∩↓SiU,An(xn)⊂T[a(x),u0]。 以下进行分情况讨论。 情况A由于|U|<|Va(x)∩↓Si|,所以∃m∈M(a(x))M(U)。因为an(xn)≥a(x),有(xn,m)∈An。由于An→A,xn→x,故(xn,m)∈A。但这与m∉M(U)和A(x)的定义矛盾。 情况C若u0∉U,取m∈M(u0),则有(xn,m)∈An以及当n→∞时(xn,m)→(x,m)。已知An→A,由此可知(x,m)∈A。但因为u0∉U,所以(x,m)∉A。因此,导出矛盾。 令vi为枝Si的上顶点,u为枝Si的下顶点,假设有某个x∈X,使得a(x)∉↓Sivi。 那么必然有如下1种情况会出现: i)a(x)>Si; ii)∃u′∈Vvi,u′∉Si,A(x)=T[Vvi,u′]; iii)A(x)=↓vi。 情况i)与引理13矛盾;情况ii)下,任取A′∈AUB(Si),则dH(A,A′)>1,与A是(An)n∈N的极限矛盾;情况iii)下,同理,任取A′∈AUB(Si),则dH(A,A′)>1,与A是(An)n∈N的极限矛盾。证毕。 由引理10、12、14,我们可以证明以下引理。 引理15对任意T上的枝Si,闭集族AUB(Si)在超空间Cld(X×T)中是闭的,其中i≤|Ts|。 由定理1和引理15,我们可以证明以下定理。 证明由定理1,有∀Si⊂T,↓CUB(Si)在AUB(Si)上稠密。由引理15知,∀Si⊂T,闭集族AUB(Si)在超空间Cld(X×T)中是闭的。
3 广义模糊函数空间的稠密性



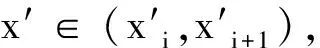
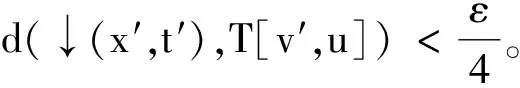





4 广义模糊函数空间的闭包