完全拉格朗日SPH 在冲击问题中的改进和应用1)
王璐 徐绯 杨扬
*(长安大学建筑工程学院,西安 710061)
†(西北工业大学航空学院,西安 710072)
引言
光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)模拟拉伸状态的粒子时,由控制方程得知粒子间会存在吸引力,有可能导致粒子聚集从而产生拉伸不稳定现象[1-2].Swegle等[3]指出当粒子的应力状态和核函数不匹配,即核函数的二阶导数与应力乘积大于零时,SPH 计算会出现不稳定现象.由此,不少学者在消除拉伸不稳定方面做了尝试:理论层面有修正核函数插值方式[4]和重构SPH 核函数[5].数值层面有密度均匀化[6]、施加人工黏性[7]、增加人工应力项[8-9]等.Belytschko等[10]认为SPH 产生拉伸不稳定性的根源在于SPH 采用的是欧拉核函数,该种核函数会扭曲材料的应力空间.此外Belytschko等[11]通过稳定性分析发现拉格朗日核函数下SPH稳定性与应力状态无关,并在此基础上提出了TLSPH(total Lagrangian SPH)方法.但由于固体边界支持域的缺失,TL-SPH 仍会面临精度不足的缺陷[12],由此本文拟在完全拉格朗日框架下推导高阶TLSPH 方程以提高整个计算域的计算精度.
SPH 粒子法的特性使得计算模型的边界条件难以像网格法一样严格实施,而SPH 界面处理对于冲击问题尤为关键.目前对SPH 界面处理技术的研究有不少成果:理论层面上,DSPH(discontinuous SPH)公式最初由Liu等[13]在处理非连续冲击波问题时提出,随后Xu等[14]将DSPH 扩展到了多维情形,并进一步提出高阶形式的DFPM(discontinuous finite particle method)方法[15],DFPM 可以改善传统SPH 方法在非连续区域上的计算精度,若将DFPM移植到完全拉格朗日框架,可提高完全拉格朗日SPH 方法对界面的模拟精度.数值层面上,由于TLSPH 中粒子的运动状态只由初始构型下邻域粒子的应力状态决定,所以需考虑冲击过程中相互作用的传递.目前SPH 方法中,虚粒子法和边界力法最为常用[16-19],但虚粒子法在复杂边界处难以实现,边界力法作用范围和强度难以控制容易导致数值振荡或穿透问题.为了避免上述弊端,本文拟在虚粒子法的基础上提出一种基于粒子间黎曼模型[20-21]的接触算法.
SPH 模拟固体的损伤破坏具有其独特的优势,不像网格法中需要定义损伤单元的删除准则,甚至需对网格进行重新划分[22-23].SPH 方法在模拟损伤破坏时,一方面可直接通过材料的本构和损伤模型体现粒子自身的损伤程度[24-25].另一方面可通过修正核函数或其作用范围实现裂纹的模拟[26].TLSPH 方法中,粒子的邻域粒子在物理演变过程中保持不变,始终是初始时刻下的邻域粒子,对破碎、断裂等间断现象的模拟能力有限.因此,需根据当前时刻粒子的损伤破坏分布,自适应地更新拉格朗日核函数.本文将在完全拉格朗日框架下提出一种损伤断裂模型以准确模拟固体冲击问题中出现的断裂现象.
综上,本文拟在TL-SPH 方法基础上,从高阶格式推导、界面处理以及损伤模型建立三个方面入手,实现对冲击问题的精确模拟.
1 TL-SPH法
完全拉格朗日框架下SPH 方法离散的固体动力学控制方程为

材料变形时粒子的柯西应力σ包括各项同性压力p和偏应力S,压力p通过式(1)中的压力-密度状态方程得到.冲击过程中材料不可避免地会进入塑性屈服阶段,粒子进入塑性阶段后,本文用Von Mises 准则[14]修正材料偏应力.
得到柯西应力σ后,粒子i的第一Piola-Kirchhoff应力Pi可由柯西应力σi经过变形梯度及其行列式转化得到[27]
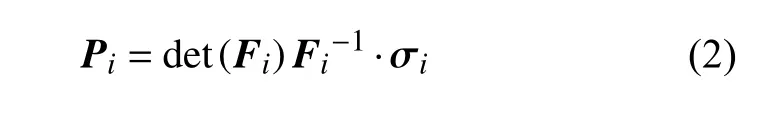
2 TL-SFPM法
SPH 核近似精度受粒子分布和支持域完整性影响,固体边界附近粒子的核估计精度会降低[5],下面在完全拉格朗日框架下推导SPH 高阶插值公式.借鉴基于当前构型的高阶插值公式的思想,以二维情形为例,将f(X)在初始构型下的点Xi处泰勒展开,省去二阶及以上导数项,分别在等式两边乘以Wi,X和Wi,Y并在Ω区域内积分,可得到[5]


式(5)可进一步整理为式(6),可以看出高阶插值公式本质是利用仅与粒子位置有关的矩阵Bi对核函数梯度做以修正.与其他高阶方法类似,式(6)会面临计算繁杂的问题.为了节省计算量,可简化参与求和粒子的选取方式.
若借鉴SFPM 方法[15]中的粒子选取方式,并充分考虑粒子间相互作用的一致性,可对称地选取距离粒子i最近的四个粒子.若粒子i位于边界,此时粒子选取方式与SFPM 方法一致.如图1 所示为规则几何构型下不同区域粒子的选取方式.

图1 规则构型下不同区域粒子选取方式Fig.1 Particles selection modes in different regions under regular configuration
下面给出不同粒子选取模式下函数梯度计算公式.假设初始时刻粒子均匀分布且粒子间距为d,光滑长度为1.2d,核函数取为常用的Wendland 核函数.此时内部区域、边界区域和角点区域的粒子对应的函数梯度计算结果如下


该种基于初始构型的选取四个粒子的函数梯度计算式所对应的粒子近似精度、一致性已在文献[28]中验证.
为了说明式(7)~式(9)的收敛性,以估计函数f(x,y)=x3+y3+2xy的梯度为例,计算域为[1,2]×[1,2].图2为不同粒子数(M)下,式(7)~式(9)计算函数∂f/∂X的均方误差MSE,为了清楚显示,坐标取为对数值.图中显示横坐标和纵坐标呈现反比例关系,当粒子间距减小,计算误差呈指数减小,说明函数梯度计算式(7)~式(9)具有收敛性.

图2 不同粒子间距下式(7)~式(9)计算三次函数∂f/∂X 的均方误差Fig.2 Mean square error of cubic function ∂f/∂X calculated by Eqs.(7)~(9) under different particle spacings
当计算域为不规则几何构型时,首先,假设计算域内部初始时刻粒子均匀分布,此时,粒子的选取方式和图1 中内部粒子一致.当粒子位于不规则的边界时,如图3 所示,则按照图1 边界粒子选取方式:首先选择粒子本身,其余粒子选为距离粒子i最近的三个粒子.此时,可根据被选择粒子与粒子i的相对位置计算式(6)即可得到函数梯度计算式.

图3 不规则计算域边界粒子选取方式Fig.3 Particles selection mode in boundary region under irregular configuration
为了保证计算的稳定性,就要保证距离粒子i最近的三个粒子不在同一条直线上.所以初始时刻离散的粒子模型应尽可能均匀分布.对于特别复杂的模型,可采用在常压p0的作用下对粒子均匀化[29].在此基础上,仍需检测所选粒子是否满足稳定性要求,如果粒子在一条直线上,那么将选择不在同一条直线的最近粒子.
本文是在二维情况下推导TL-SFPM 方程,高阶插值公式(6)可通过增加维度扩展至三维,这构成了TL-SFPM 方法应用于三维问题的理论基础.借鉴SFPM 方法[15]以及充分考虑粒子间相互作用的一致性,三维情况下,当粒子在空间均匀分布时,可对称地选取以粒子i为中心的六面体上距离最近的六个粒子,与二维类似,此时粒子i与被选取粒子的间距均为d.当粒子位于边界或者角点时,首先选择粒子本身,其余粒子选为距离粒子i最近的五个粒子.上述三维模拟策略仍需进一步验证.
下面介绍TL-SFPM 方法中不同物理量梯度的求解式.
2.1 变形梯度求解
作为初始构型和当前构型之间的桥梁,粒子的变形梯度Fi是关键物理量.使用式(7)~式(9)可分别得到内部区域、边界区域和角点区域粒子变形梯度Fi的计算式为


式中,u,v分别为粒子x方向和y方向的位移,下标数字(1,2,3,4)与图1 的粒子编号对应,I为单位矩阵.
2.2 加速度求解
若直接使用式(6) 求解加速度方程中的第一Piola-Kirchhoff 应力P的梯度,此时会导致粒子i与j之间相互作用不一致,破坏守恒关系.为了维持守恒关系,下面推导加速度方程.
在不考虑人工黏性条件下,TL-SPH 求解加速度方程为[27]

若使用高阶插值公式修正核函数梯度,加速度方程可改为[30]

可以看出,该式可保证mi(dvi/dt)j→i=-mj(dvj/dt)i→j,粒子i对粒子j的作用力与粒子j对粒子i的作用力一致.若考虑人工黏性,将人工黏性直接加到加速度方程即可

上式并未修正人工黏性项,这是由于该项所占比重较小,为了节省计算时间直接使用传统核函数计算.为了与变形梯度计算保持一致,加速度计算仍采用图1 所示的粒子选取方式,此时,加速度方程写为

3 界面处理
3.1 TL-DFPM法
DFPM 方法是一种考虑界面不连续的高阶离散方法,它基于界面处物理量的不连续性,在非连续区域两边分别进行连续性修正,且可避免不连续位置的确定[15].为了提高TL-SPH 方法在界面处的精度,本节拟将DFPM 方法引入完全拉格朗日框架中.
如图4 所示为二维情形下的不连续计算域示意图,Ω为粒子的整个支持域,Ω1和Ω2为其子域,Ω1和Ω2之间不连续界面为Γ(Ω1∪Ω2∪Γ=Ω).

图4 二维情形下的不连续计算域示意图Fig.4 Discontinuous computational domain in 2-D
二维情形下DFPM 方法的基本方程[15]为

式中,Vj为邻域粒子j的体积,f,x(xi)=∂f(xi)/∂x,f,y(xi)=∂f(xi)/∂y,Wij,x=∂Wij/∂x,Wij,y=∂Wij/∂y,x,y为当前构型下的坐标分量.上式只考虑了邻域内与粒子i同侧的粒子信息.通过非连续性近似分析,该修正式可以保证梯度计算的精确性,也能够实现不连续界面处粒子信息的准确估计.若将上述方法引入完全拉格朗日框架中,可得

可以看出上式将式(6)方程中的所有邻域粒子求和修正为子域Ω1内的粒子求和,这可以避免异侧子域Ω2粒子物理信息间断带来的误差.基于此,界面处TL-SFPM 方法中四个粒子的选取方式可修正为图5 所示方式,界面附近粒子被当作边界粒子处理.

图5 界面处TL-SFPM 方法中四个粒子的选取方式Fig.5 Particles selection mode at interface in TL-SFPM method
3.2 接触模型——黎曼接触法
为了保证界面处的粒子计算精度,式(19)将子域Ω1粒子的计算与子域Ω2区域隔离开,这时需引入不同区域间的接触模型,定义粒子i和j间的相互作用.本节将提出基于黎曼解的接触算法.
如图6 所示为SPH 粒子间黎曼模型示意图,假设粒子间存在间断面,将其相互作用按照连续介质中的间断问题处理,间断界面位于中心点(ri+rj)/2处,此时,间断面左侧密度、速度、压力和声速为

图6 SPH 粒子间黎曼模型Fig.6 Riemann model with SPH particles

间断面右侧密度、速度、压力和声速为

式中,eij=为粒子i指向粒子j的单位向量.若通过求解该黎曼问题得到中间应力p*,将其代入粒子i动量方程中,即可实现异侧粒子j对粒子i的作用力fij,fij的具体表达式为式(22).很明显fij=-fji,满足相互作用的一致性

式中,p*为压力黎曼近似解,一种近似的线性解为[31-32]

3.2.1 流固接触
SPH 在利用虚粒子方法施加流体的边界条件时,需在初始阶段提前布置虚粒子,其位置固定或者由流体粒子镜像决定.这种策略往往比较费时且对复杂边界受限[33].然而该种方法能够保证守恒性,且滑移与无滑移边界条件易实现[34],为了保留该方法的优势,本节将修正虚粒子方法提出动虚粒子黎曼法.
动虚粒子黎曼法的具体措施:将固体粒子i看作提前布置的虚粒子,然而该种虚粒子位置并不固定,根据自身的运动方程更新其位置.可以赋予该种动虚粒子新的物理量——虚压力,虚压力通过流体压力插值得到[34],即

式中,f为固体粒子i邻域内的流体粒子,Wif为核函数,ai为固体粒子自身的加速度,g为重力加速度.得到虚压力后,流固间相互作用可通过式(22)实现,此时,pL为固体粒子虚压力,pR为流体粒子压力pf,ρL和cL为固体粒子密度ρi、声速ci,ρR和cR为流体粒子密度ρf、声速cf.vL为动虚粒子即固体粒子速度vi,vR为流体速度vf.此时,固体粒子i所受到来自流体的外力fif为

式中,pif*为固体粒子i和流体粒子f之间的近似压力黎曼解.
3.2.2 固固接触

该压力不同于式(1)状态方程求解的压力,仅用来求解固体间接触力.当不同固体材料相互作用时,黎曼问题的左状态物理信息为固体粒子i的密度pi、速度vi、压力和声速ci,右状态物理信息为固体粒子j的密度pj、速度vj、压力和声速cj.通过式(22)即可得到粒子i和j间的相互作用力fij.
4 粒子损伤破坏模型
粒子损伤累积到一定程度后会发生破坏,定义损伤因子D描述损伤程度[26],D的范围为0~ 1,D=0时,粒子未发生破坏,D=1 时,粒子完全破坏,0<D< 1 时,粒子发生部分破坏,表明与周围粒子的相互作用减弱.不同材料根据材料特性有不同形式的损伤因子式.SPH 方法是利用核函数衡量粒子间的相互作用,因此可通过下列修正体现粒子损伤后与邻域粒子相互作用的减弱

5 算例验证
5.1 流固冲击——带弹性挡板溃坝
这节以流固耦合冲击问题为例验证本文提出的TL-SFPM 方法和界面处理技术的优势.如图7 所示,红色区域为弹性挡板,上端与刚性固壁固连,挡板内蓝色区域为水,在重力作用下,水坍塌冲击弹性挡板,挡板发生变形.挡板的材料参数和模型几何尺寸见表1.水初始密度为1000kg/m3,水近似为弱可压模型[35-36],用低耗散GSPH 方法计算.低耗散GSPH 方法离散流体的控制方程如下[37]

图7 带弹性挡板溃坝模型Fig.7 Model of the dam with elastic baffle

表1 弹性挡板材料参数Table 1 Material parameters of elastic baffle

式中v*和p*是速度和压力的近似黎曼解[37].低耗散GSPH 中,为了降低耗散导致流动失真,将p*中的声速限制为[38]

式中,假设流体粒子i和j的声速保持一致为c0,ω为常数,该算例中取1.0.该算例流固接触模型使用第3 节的黎曼接触算法.
图8为不同粒子间距下,水采用低耗散GSPH方法,弹性体采用TL-SFPM 方法的策略下,弹性挡板自由端竖直位移变化曲线,可以看出粒子间距减小到一定程度时,位移变化趋于收敛.为了保证一定的计算精度和效率,本算例选取粒子间距为0.5 mm.

图8 不同粒子间距弹性挡板自由端竖直位移变化曲线Fig.8 Vertical displacement of the free end of elastic baffle with different particle spacings
为了说明TL-SFPM 方法相比传统TL-SPH 方法的优势,图9(a)比较了相同分辨率下,TL-SFPM方法和传统TL-SPH 方法模拟的弹性挡板自由端水平和竖直位移变化曲线,可以看出TL-SFPM 的结果与试验[39]的结果更吻合.对比二者模拟结果,在位移增大的过程中,TL-SFPM 的结果较大,在达到最大位移后,反而位移较小,这是由于TL-SFPM 方法修正了边界区域的一致性,在计算变形梯度或压力梯度时更精确.图9(b)也对比了挡板附近水面高度随时间的变化曲线,TL-SFPM 仍然与试验更吻合.图10给出不同时刻模拟得到的粒子分布与试验形态对比图,结构变形和流体坍塌形状均与试验保持一致.但是试验中可以观测到有部分水从挡板两端喷溅出,而模拟的二维模型并未出现该现象.这是由于:(1) 试验是三维模型,水可从挡板两端逃逸;(2)为了计算稳定,低耗散GSPH 方法会稍微增大水的耗散,导致水飞溅的现象并不明显.

图9 弹性挡板和液面位置随时间变化曲线Fig.9 Curves of the elastic baffle and the water surface positions

图10 TL-SFPM 模拟结果和试验结果[39]对比图(自0~0.32 s,每隔0.08 s)Fig.10 Comparison of TL-SFPM simulation and experiment results[39]from0s to0.32 s(at0.08 s intervals)
图11 对比了某一时刻TL-SFPM 方法和文献[39]得到的弹性板应力分布云图,可以看出本文得到的应力分布更加稳定均匀,文献中的结果仍存在应力震荡现象.其原因可能是:一方面,文献[39]中采用人工应力法改善拉伸不稳定,而本文使用的是TLSFPM 方法.另一方面,本文采用的是基于黎曼解的接触算法,文献[39]中使用的是传统虚粒子算法.

图11 TL-SFPM和文献[39] 模拟得到某时刻弹性挡板y 方向应力分布云图Fig.11 Stress distribution at y-direction of the baffle obtained by the TL-SFPM and Ref.[39]
表2 比较了TL-SFPM 方法和TL-SPH 方法在Intel(R) Core(TM) i7-3770八核心处理器下的计算时间.可以看出TL-SFPM 相比TL-SPH 可节省一定的计算时间,这是因为TL-SFPM 中邻域内参与计算的粒子数相比TL-SPH 更少.虽然TL-SFPM 方法采用的是高阶格式,但是由于初始构型下粒子相对位置确定,高阶格式的修正矩阵Bi只需在初始时刻计算一次,后续直接调用即可.二者计算时间相差并不大是因为本算例中弹性体粒子数所占总粒子数比重较少,而且两种方法均需基于当前构型计算流固接触力.

表2 TL-SPH和TL-SFPM 模拟时间对比Table 2 Computational time with TL-SPH and TL-SFPM methods
5.2 固固冲击——子弹撞击靶板
这节以子弹撞击靶板算例验证本文提出的TLSFPM 方法、界面处理技术以及损伤破坏模型的合理性和精确性.圆头的钢弹撞击铝合金的飞机蒙皮[40],弹丸直径12.7 mm,长度51 mm,靶板长和宽均为300mm,厚3 mm,子弹以150m/s 速度向右冲击铝板,子弹和靶板均采用Johnson-Cook 本构模型,具体材料参数见表3,表中参数含义与Johnson-Cook 本构模型一致.

表3 钢和铝材料参数Table 3 Material parameters of steel and aluminum
5.2.1 无损伤破坏模型
首先在该模型中不加入材料的损伤破坏模型以验证TL-SFPM 方法改善拉伸不稳定的能力.可以分别用传统高阶SPH 方法——CSPM(corrective smoothed particle method)[3]和TL-SFPM 计算该模型.图12给出某时刻钢弹以150m/s 的速度撞击铝板后子弹和铝板的速度云图及局部放大图,从图可以看出:(1) CSPM 结果中,在子弹撞击铝板后,铝板出现了一定程度的破坏,并且在铝板的变形两端也出现了不同程度的断裂,出现了粒子聚集现象,这体现了传统SPH 拉伸不稳定的缺陷;(2)同一时刻TL-SFPM方法模拟的结果并未出现断裂现象,粒子分布及速度分布整齐且均匀,改善了拉伸不稳定缺陷.图13为TL-SFPM和有限元(FEM)模拟的不同时刻子弹和铝板的速度云图,看出两种方法得到的结果吻合,速度分布均匀,这验证了TL-SFPM 方法具有较好的精度.

图12 CSPM和TL-SFPM 得到钢弹撞击铝合金板同一时刻速度分布云图Fig.12 Velocity distribution obtained by the traditional SPH and high-order TL-SPH

图13 TL-SFPM和有限元模拟的不同时刻子弹和板的速度(m/s)云图Fig.13 Velocity(m/s) distribution at different times obtained by TL-SFPM and FEM
5.2.2 有损伤破坏模型
若在计算中加入以下损伤因子

即当粒子的塑性应变εpl累积到一定值时,粒子发生破坏,该算例εpl,max取为0.12.图14 给出TLSFPM 计算得到的不同速度下靶板的破坏形态,绿色为破坏粒子.从图中看出不同速度下铝板的破坏模式不同.速度为150m/s 时,铝板在撞击部位出现张开的裂纹,随着钢弹向右运动,裂纹不断张开直到钢弹穿过板.当钢弹速度为300m/s 时,首先铝板的内部在冲击部位两侧发生破坏,接着裂纹不断扩展,形成了碎片.当钢弹速度增大到500m/s 时,铝板首先在与钢弹接触部位发生破坏,最终形成了更小的碎片.

图14 加入断裂模型后不同冲击速度下的失效粒子分布Fig.14 Distribution of failure particles at different impact velocities with the fracture model
图15为钢弹剩余速度,铝板的变形直径和弹坑深度随冲击速度的对比曲线,CSPM 由于会出现数值断裂导致和试验[40]相差较大,而TL-SFPM 与试验吻合较好,表明只有改善数值断裂现象,才能模拟出精确的结果.

图15 钢弹冲击靶板计算结果与试验结果对比[40]Fig.15 Comparison of the steel projectile impacting the aluminum alloy plate results between simulation and experiment[40]
表4 比较了TL-SFPM 方法和CSPM 方法在Intel(R) Core(TM) i7-3770八核心处理器下的计算时间.可以看出TL-SFPM 方法相比CSPM 方法计算时间略长,虽然TL-SFPM 方法可节省粒子邻域搜索的时间,但是当粒子进入塑性后,TL-SFPM 方法的计算过程相比CSPM 更复杂,需要将柯西应力σ转化为第一Piola-Kirchhoff 应力P.另外,TL-SFPM 方法断裂模型中需要及时对核函数更新.当不同材料作用,TL-SFPM 也需在每一时间步内计算当前构型下的压力黎曼近似解p*以求解不同材料间的接触力.

表4 CSPM和TL-SFPM 模拟时间对比Table 4 Computational time with CSPM and TL-SFPM methods
6 结论
本文针对传统SPH 模拟固体时出现的拉伸不稳定缺陷提出了高阶格式的完全拉格朗日SPH 方法——TL-SFPM 方法,并分别推导了变形梯度和加速度方程的离散格式.此外,在完全拉格朗日框架下,分别从理论和数值方面提出了TL-DFPM和黎曼接触法,形成了双重耦合的界面处理技术.在此基础上,建立完全拉格朗日框架下的损伤破坏模型以准确获得固体粒子损伤破坏程度.通过带弹性挡板溃坝算例验证了TL-SFPM 方法相比已有的消除拉伸不稳定策略的优势,也说明了基于黎曼解接触算法的适用性和精度.通过子弹撞击靶板算例验证了TLSFPM 方法可以较好地避免拉伸不稳定导致的数值断裂.在此基础上,加入物理断裂模型分析靶板撞击后的损伤模式,不同撞击速度下靶板的破坏模式差异较大,低速时靶板出现断口较平齐的裂缝,而高速下靶板会产生碎片.通过与试验中子弹的剩余速度、靶板变形直径和弹坑深度对比验证了本文提出算法的有效性和精度.
本文提出的TL-SFPM 方法,在具备可观计算效率的前提下提高了冲击荷载下固体动态响应的计算精度,同时具有损伤破坏模型易施加、三维易扩展等优势,对于流固耦合、固体冲击等问题的高精度数值模拟具有广阔的应用前景.

