模型建构:从无到有的嬗变
——以微专题“构造‘手拉手’模型求最值”为例*
赵 军 (江苏省太仓市实验中学,太仓市赵军名师工作室 215400)
《义务教育数学课程标准(2022年版)》在核心素养的主要表现及其内涵中,要求初中阶段的模型观念应具备:对运用数学模型解决实际问题有清晰的认识,知道数学建模是数学与现实联系的基本途径;初步感知数学建模的基本过程,从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义[1].在解题过程中,合理的模型建构能够帮助我们对问题进行高效的转化,在平时学习过程中如果多留意归纳积累数学基本模型,并理解其内涵本质,关键时刻可以巧建模型,从容应对.事实证明,合理的模型建构往往能大幅度提高解题的效率,提升数学素养,达到化难为易的目的.笔者尝试以建构“手拉手”等边三角形(共顶点等边三角形)和“手拉手”等腰直角三角形(共顶点等腰直角三角形)解题为例,对一类求最值问题进行专题剖析,以期与同仁交流与分享.
1 课堂实录与点评
师:同学们,首先我们来一起回顾课本上的一个基本模型——“手拉手”等边三角形,请大家先看原题.
1.1 原题再现
(苏科版教材八年级上册第67页第10题)如图1,△ABC和△CDE都是等边三角形,点A,C,E在一条直线上,AD与BE相等吗?为什么?

图1
生1:相等,借助等边三角形的性质,运用“SAS”证明△ACD≌△BCE即可.
师(追问):若将△ACD绕点C顺时针旋转(如图2)或逆时针旋转(如图3),AD与BE还相等吗?

图2 图3
生2:相等.证明方法仍然是用“SAS”证全等,只不过图2中的∠ACD=∠BCE是“同加”得到的,图3中的∠ACD=∠BCE是“同减”得到的.
师:很好!这是一个基本的数学模型,由于两个等边三角形共顶点,我们把它称之为“手拉手”等边三角形模型.下面我们一起来看看这个模型在求最值问题中的应用.
设计意图从课本原题出发,通过适当的旋转,带领学生体会“形变法不变”的思路,归纳出“手拉手”模型的结论,为后续建构模型和运用模型作好铺垫,同时也凸显了课本习题作为“题根”的价值.
1.2 若隐若现
问题1如图4,等边三角形ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连结AD并将AD绕点A逆时针旋转60°至AE,连结EF,则EF的最小值为.

图4
师:同学们,随着点D的运动,点E随之而变化,导致EF的长度也在变化,如何确定EF的最小值呢?
生3:若连结DE,作直线CE,则图4属于图3中的“手拉手”等边三角形模型,并有△ABD≌△ACE.
师(追问):这个全等有什么作用呢?
生4:由全等可以得到∠ABD=∠ACE=30°,结合∠ACB=60°可得BC⊥CE.
师(再追问):太牛了!借助“手拉手”等边三角形模型,我们发现点E运动的轨迹是什么呢?
生4:点E在过点C且垂直于BC的直线上运动.
师:那什么时候EF最小呢?

师:太棒了!
设计意图通过教者适时的引导,“手拉手”等边三角形模型自然浮出水面,在探究出点E运动轨迹的基础上,将最值问题转化为点到直线距离最短问题,体现了对该模型的挖掘与应用.
1.3 模型重现
问题2如图5,已知矩形ABCD中,AB=4,AD=6,点P是边AD的中点,点E为边CD上的一个动点,连结PE,以PE为边向下方作等边△PEG,连结AG,则AG的最小值是.

图5 图6
师:同学们,我们该如何对AG进行转化?
生5(若有所思地):以AP为一边构造等边三角形,利用“手拉手”等边三角形模型对AG进行转化.
师(追问):请具体一点.
生6(激动地):如图6,在AP的下方作等边△APF,连结EF,则△APG≌△FPE(SAS),所以AG=FE,因此求AG的最小值就是求FE的最小值.
师:分析得很到位!那如何求FE的最小值呢?
生6:由于点E为边CD上的一个动点,所以问题转化为点F到CD的距离FM(如图6).
师(追问):很好!那么怎么求FM呢?

设计意图通过教师巧妙地设问和不断地追问,在三位学生的接力回答下,将隐形的“手拉手”等边三角形模型建构得恰到好处,把求AG最小值的问题不断转化,步步深入,达到了化难为易的效果.
问题3如图7,△ABC是等边三角形,E,F分别是经过点B的直线l上的两点(E,F位于点B的异侧),连结AE,CF.若BE=2,BF=4,则AE+CF的最小值为.

图7
师:△ABC是一个边长不确定的等边三角形,所以AE和CF的长度随之而变化,如何通过转化将这两个分散且变化的线段进行关联?
生8:我想再作一个等边三角形,利用“手拉手”等边三角形模型对AE和CF中的某条线段进行转化.
师(追问):具体如何构造呢?请大家分小组讨论.
生9(第1小组代表):如图8,我们小组是以BF为边在直线l的上方作等边△BFD,则△BCF≌△BAD,所以CF可以转化为AD,问题即转化为求AE+AD的最小值,在等边△ABC变化的过程中点A是动点,点E,D是动点,所以问题可以转化为“两点之间,线段最短”,即其最小值为DE的长.

图8
师(追问):很好!那又如何求DE呢?
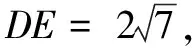
师:还有不同意见吗?


图9
师:说得真好!这两组同学完成得都很棒!那么比较一下,这两种构造有何异同呢?
……
设计意图第一小组学生以线段AE不动,构造“手拉手”等边三角形模型去转化CF,第二小组学生以线段CF不动,构造“手拉手”等边三角形模型去转化AE,两种构造思路有异曲同工之妙!无论是哪一种构造,本质上都是将两条线段转化至首尾相连,以“两点之间,线段最短”解决问题.
1.4 类比重建
问题4如图,在ABCD中,∠B=45°,M是AB边的中点,N是BC边上的一动点,将线段MN绕点M逆时针旋转90°至MN′,连结N′C,N′D,若BC则N′C+N′D的最小值是.

图10
师:同学们,在问题3中我们构造的是两个共顶点的等边三角形,现在在问题4中,我们又将如何构造呢?请大家分组进行探究.
(几分钟之后,教师请各小组代表发言)
生11:求N′C+N′D的最小值的关键是对其中某一条线段进行转化,我们小组研究的意见是连结N′B,将N′C转化为N′B,最终将最小值转化为线段BD的长.
师:很好的想法!那怎样证明N′C=N′B呢?
生12(补充):如 图11,因为MN绕点M逆时针旋转90°至MN′,就相当于△MNN′(连结NN′)为等腰直角三角形,类比前面几个问题的方法,以点M为直角顶点再构造一个等腰直角△MBE.这样就构造出两个共顶点的等腰直角三角形,运用“SAS”得到△MBN≌△MEN′.

图11
师(追问):接着是怎样得到N′C=N′B的?请具体一点.
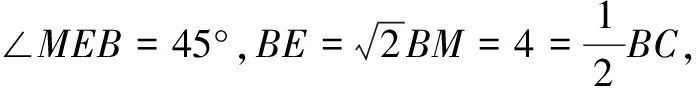
师:太厉害了!此时N′C+N′D就转化为N′B+N′D,所以点N′运动的轨迹是什么?
生13:点N′在BC的垂直平分线上运动.
师:真聪明!那最小值怎么求?

师:通过构建等腰直角三角形、转化线段,再构造直角三角形解决问题,太棒了!
设计意图“手拉手”模型的建构不仅仅局限于两个共顶点的等边三角形,还可以构建共顶点的等腰直角三角形,其构建的灵感来源于45°角的出现.在解决前几个问题的铺垫下,教师引导学生展开深入探究,学生在探究过程中努力建模,形成能力,学会解决问题的方法,提升数学素养.
师:通过这节课的探究,大家有哪些感悟与收获呢?
生15:当出现“手拉手”模型的一只手时,我们要学会构建另一只手.(赢得掌声)
生16:构建“手拉手”模型源于转化的需要,当我们“无路可走”时要能主动建模!
……
师:建模相当于“无中生有”,是在已有条件的基础上重建,需要平时的积淀,更需要衔接技巧和转化得当.已知一手,巧建另一手,方能大手拉小手,实现拨云见天,柳暗花明!
2 教学反思
2.1 模型建构的基础始于模型的积累
模型建构的难点在于建,从哪里入手去建模?怎样建?没有一定的积累无法完成模型的建构.建模既要充分考虑学生的学习情况,尤其是学生的“最近发展区”,也需要结合题目自身的条件进行分析.一般而言,从条件出发,由“已知想可知”;从结论出发,由“未知想需知”,两头往中间推理,查找缺什么.而后缺什么就补什么,此时自身对数学模型的积累显得尤为重要,关键时候要能结合题目联想到需要的模型.因此,我们可以在每章节学习结束后结合课本内容进行归纳、提炼,平时要善于总结,形成适用的基本模型,归纳出属于自己的“定理”.可能还有学生会质疑,在建模的过程中,你是怎么想到某种构造方法的?实际上还有另一个解题的关键点:运动的轨迹是什么?依据动点的运动路径可以管窥一二,因为此类问题往往聚焦点的运动而带动图形的运动,类似问题1和问题4中寻找点的运动轨迹,以“始动点”在运动初期、运动过程中和运动结束三个时点为基点,分别探寻“从动点”运动的路径以清晰建模的路径.
2.2 模型建构的思路源于转化的内需
模型建构的内需源于解题不畅,需要转化,如何寻找替换对象是解决问题的关键.从问题2到问题4的顺利解决不难发现,对于线段的转化往往依据全等,从全等的条件探寻中你会感受到有建模的需要,通过全等模型的建构能达到转化的目的,所以建模不是刻意为之,也不是为建模而建模,它是解决问题的内在需要.每当山穷水尽之时,我们可以结合自身数学模型的积累,尝试通过建模进行转化,建模得当往往能够柳暗花明.《义务教育数学课程标准(2022年版)》在课程性质中明确指出,基于抽象结构,通过对研究对象的符号运算、形式推理、模型构建等,形成数学的结论和方法,帮助人们认识、理解和表达现实世界的本质、关系和规律[1].所以建模也是一种对自身阶段学习内容的提炼和归纳,更是应用模型解决问题的需要,我们要能将解题需要和模型积累通过分析进行有效的衔接,以达到转化的目的.
2.3 模型建构的理念凝于认知的高度
模型建构是一种高屋建瓴的高观念,通过建模可培养学生的学科思维,帮助学生建立模型思想,以增强学生数学学科关键能力.模型意识或模型观念是数学思维的主要表现形式,以数学模型为中心的学习能够帮助我们提炼学习内容,吸收更多概括化了的基本原理或思想,深思数学学科本质,促进有意义有深度的学习.从问题1中已有的“手拉手”等边三角形雏形到问题2和问题3中的主动构建“手拉手”等边三角形,再到问题4中的类比构建“手拉手”等腰直角三角形,4个问题的建模不断深入,从教学设计和课堂实践不难发现,数学基本模型的归纳与提炼有利于数学学科知识的建构、学科思维的形成和学科方法的掌握,数学模型的建构能使学生的认知结构梯度上升,从而获得学习之精髓、学科之价值.作为教师应带领学生以模型建构为抓手,以问题转化为目的对数学解题进行深入研究,引领学生学思相融、学以致用,进而提高建模能力、提升数学素养.

