双曲型方程激波捕捉的物理信息神经网络(PINN)算法
郑素佩,靳放,封建湖,林云云
双曲型方程激波捕捉的物理信息神经网络(PINN)算法
郑素佩,靳放*,封建湖,林云云
(长安大学 理学院,陕西 西安 710064)
双曲型方程的数值求解算法研究一直是偏微分方程研究的热点,其中,双曲型方程的间断捕捉是难点。受物理信息神经网络(physics-informed neural networks,PINN)启发,构造了改进的PINN算法,近似求解双曲型方程的间断问题。将坐标构造的数据集作为神经网络的输入,将PINN算法中的损失函数作为训练输出值与参考解(基于细网格的熵相容格式数据)或准确解的误差值,通过网络优化,最小化损失函数,得到最优网络参数。最后用数值算例验证了算法的可行性,数值结果表明,本文算法能捕捉激波,分辨率高,且未产生伪振荡。
双曲守恒律方程;网络预测;物理信息神经网络(PINN);激波捕捉
双曲守恒律方程是一类较特殊的偏微分方程,可用于描述流体受力运动的欧拉方程、导电流体在磁场中运动的磁流体方程、海洋流体运动的浅水波方程等实际问题。双曲守恒律方程的显著特性之一是即使初始条件是光滑的,其解也可能是间断的。正确理解双曲守恒律方程的特性,并设计合理的数值格式,对数值模拟实际问题非常重要。目前已有许多有效的方法,如迎风格式、Lax-Friedrichs格式、ENO/WENO(essentially non-oscillatory/weighted essentially non-oscillatory)格式[1]、熵守恒格式、熵稳定格式[2]及在这些格式上改进的算法[3-5]。
除以上传统数值求解算法外,近年来,深度学习在求解偏微分方程中的应用研究也取得了大量成果[6-8]。深度学习作为一种现代数值计算方法被应用于医学影像、自然语言处理、工程等领域[9],被认为是一种最先进的分类和拟合函数工具。万能近似定理[10]表明,如果前馈神经网络具有线性输出层和至少一层“挤压”激活函数隐藏层,那么只要给予网络足够数量的隐藏单元,就可以任意(高)精度逼近任何从一个有限维空间到另一个有限维空间的Borel可测函数[11]。CHEN等[12]指出,用一个单一的隐藏层神经网络可以任意精度逼近任何函数,这说明神经网络实际上可以以任意高的精度逼近原函数,甚至逼近非线性算子,即神经网络是通用的函数逼近器。目前,最具代表性的基于深度学习求解偏微分方程的工作是物理信息神经网络(physics-informed neural networks,PINN)[13],并广受关注[14-16]。PINN可利用前馈神经网络直接处理原始偏微分方程,通过将偏微分方程作为正则化项加入损失函数,即在神经网络中加入了偏微分方程的物理规律。经此处理使得训练过程中只需要少量的数据便可得到可靠的结果,加快了训练的过程。PINN在处理连续问题及反问题时取得了很大成功,但在处理具有不连续解的双曲守恒律方程时性能较差。例如,当被用于处理Burgers方程时,为防止伪振荡,通常需添加黏性项。如果黏性项消失或黏度系数很小,PINN就很难训练,亦无法捕获激波。
对于双曲守恒律方程,由于其解易发展为间断,因此,在间断附近需慎用传统数值算法。为此,本文基于PINN的思想,将坐标构造的数据集作为神经网络的输入,将损失函数作为训练的输出值与所给数据的误差值,提出了一种改进的PINN算法,用于求解双曲守恒律方程的间断问题,数值结果表明,所提算法可以捕获激波且未产生伪振荡。
1 双曲型方程及传统求解格式
1.1 双曲型方程
一维方程组:
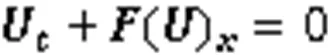
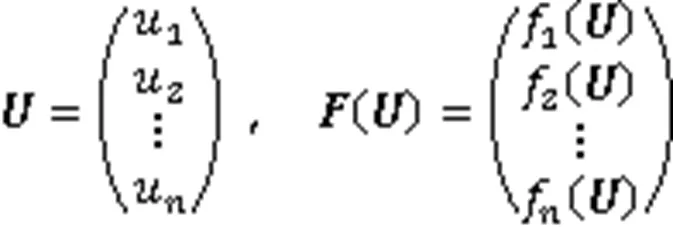
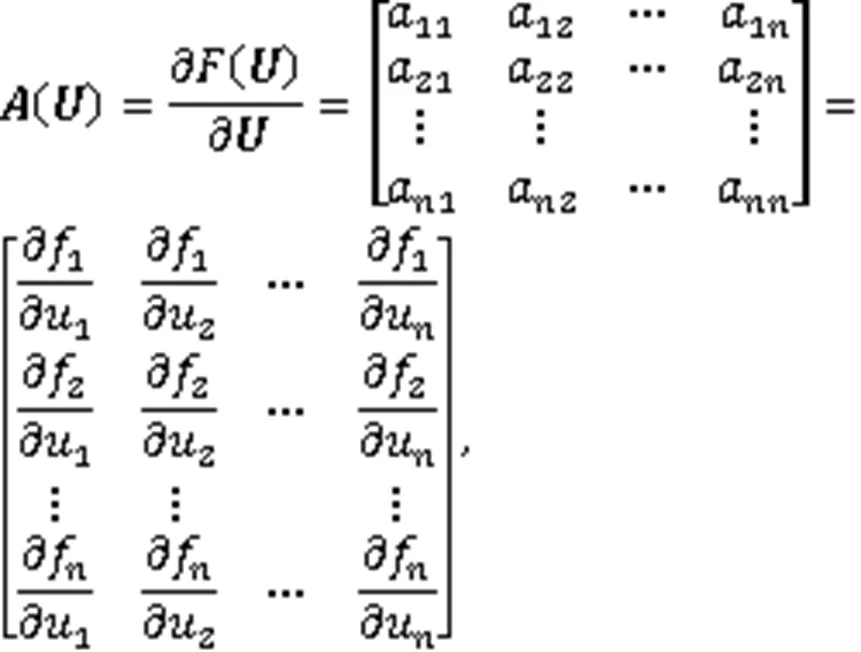

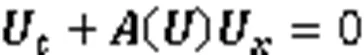
对于特征多项式方程:
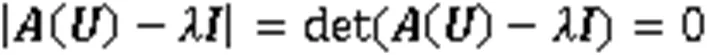

对于二维方程组:

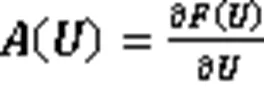
由链式法则,式(2)可改写为拟线性形式
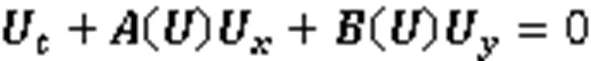
1.2 熵相容格式
二阶熵守恒格式在光滑解区域效果很好,但在间断区域会产生振荡。ROE[17]在熵守恒格式基础上通过添加数值黏性项,得到了一类熵稳定格式。用此格式求解双曲守恒律方程,当跨越激波时,会产生激波强度三次方量级的熵增,因此,需添加耗散项,以控制激波处的熵增。ISMAIL等[2]将左右特征速度差分的绝对值添加至数值黏性项,让其产生足够的熵耗散,以消除熵增量,确保格式的熵稳定。熵相容格式的数值通量式为
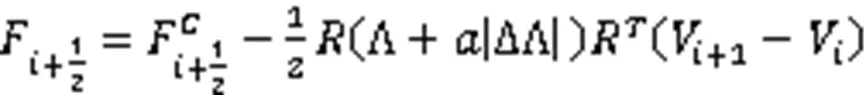
2 改进的PINN算法
PINN算法利用前馈神经网络,通过在损失函数中加入偏微分方程,将偏微分方程作为正则项,将物理信息引入神经网络,在处理连续问题及反问题时取得了成功,但在处理具有不连续解的双曲守恒律方程时性能较差。由于激波由多条压缩波相交而成,可导致熵增等,所以仅用方程控制损失函数,无法解释其包含的物理特征,造成PINN算法在求解双曲守恒律方程间断问题时效果不好。为此本文提出了改进的PINN算法。

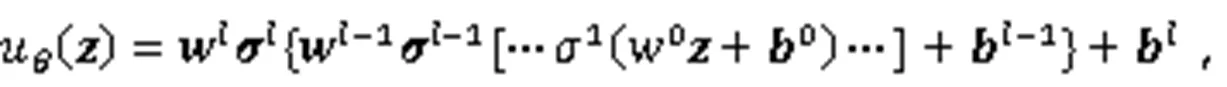
最小,其中,
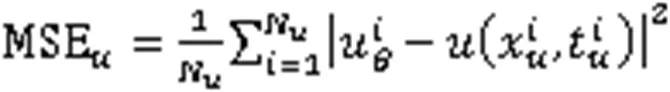
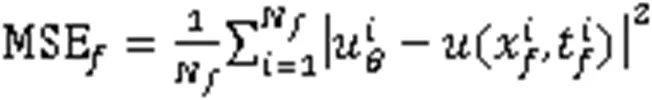
PINN中原损失函数的定义为
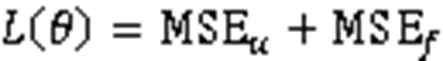
其中,
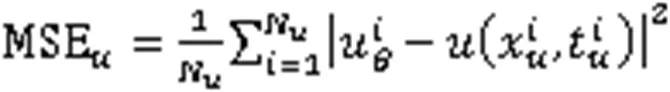
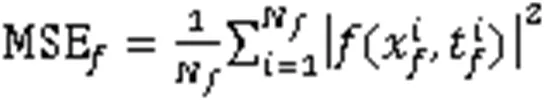
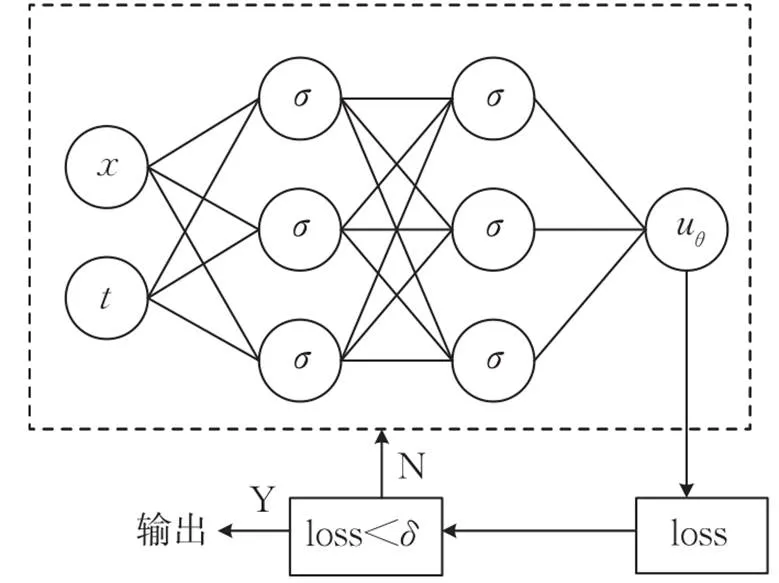
图1 改进的PINN算法的网络结构
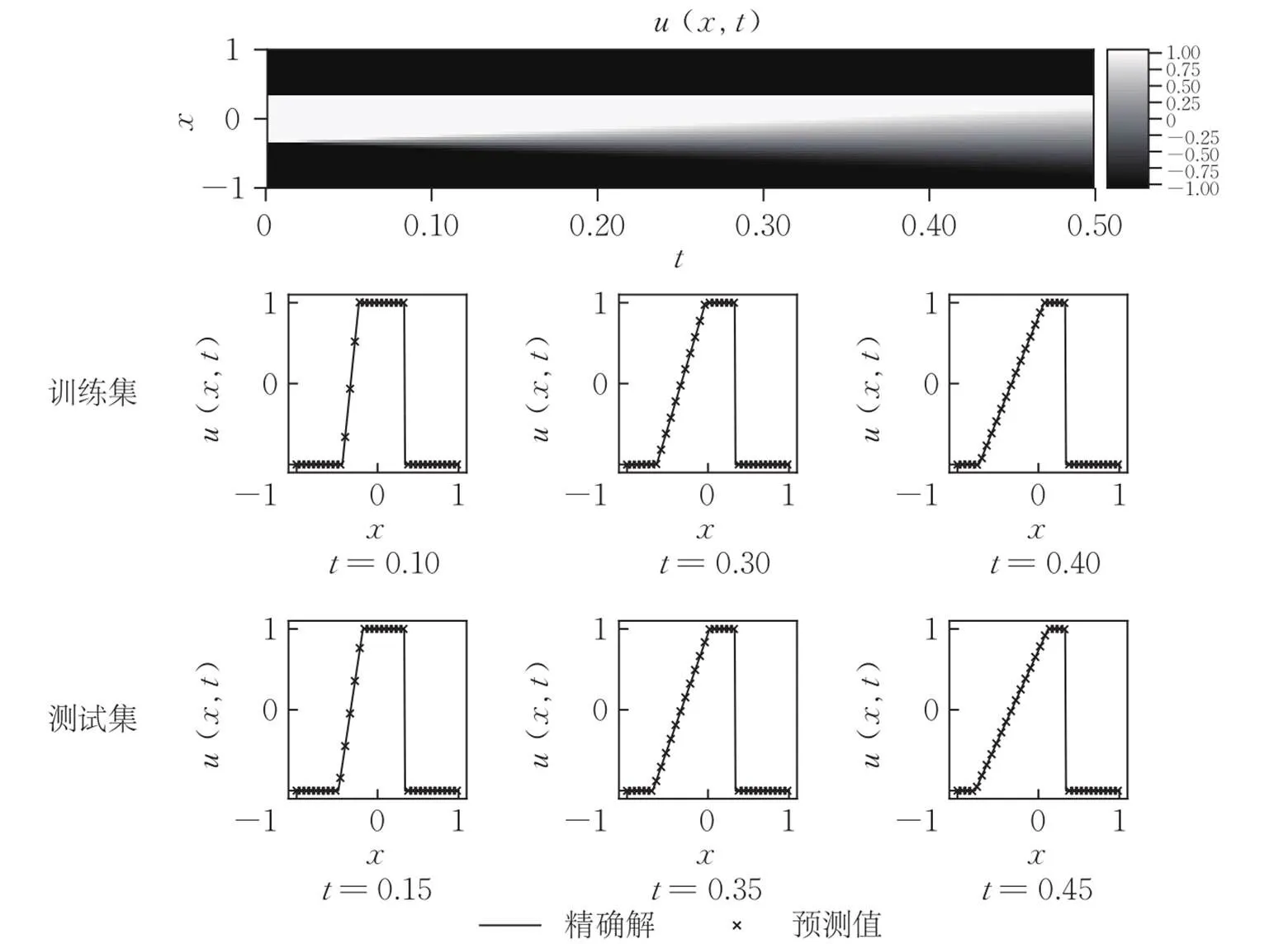
图2 无黏Burgers方程训练集、测试集预测值与精确解的比较
3 数值算例
用类PINN算法求解一维、二维双曲型方程间断问题。在所有算例优化过程中,只对隐藏层使用tanh激活函数,输出层未使用激活函数。为检验训练模型的性能并防止过拟合,以下所有算例的数据均按空间层均匀选取,按8∶2的比例将时间层分为训练集和测试集,其中测试集数据由隔点取样方法得到。
算例1 无黏Burgers方程
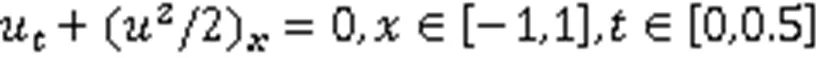
满足初始条件:
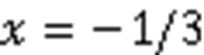
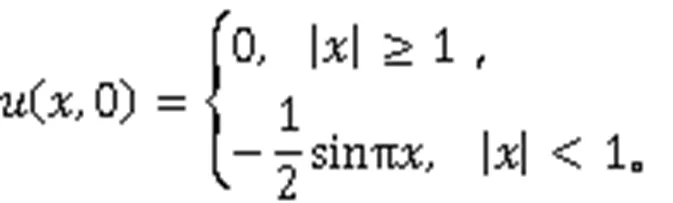
图3 无黏Burgers方程压缩波训练集、测试集预测值与精确解的比较
Fig.3 Comparison of prediction training set, prediction test set and exact solution of compressible waves of non-viscosity Burgers equation
算例3 线性对流方程
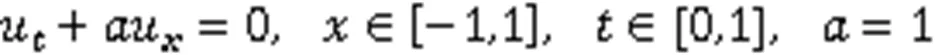
满足初始条件:
其中,


图4 线性对流方程压缩波训练集、测试集预测值与精确解的比较
Fig.4 Comparison of prediction training sets, prediction test sets and exact solutions for linear convection equations
算例4 一维Euler方程Sod激波管问题。
一维Euler方程
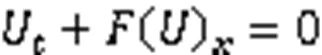
其中,
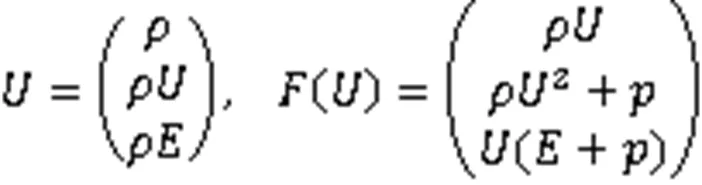
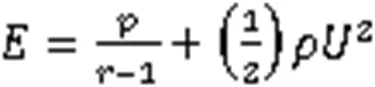

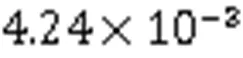
图5 Euler方程压缩波训练集、测试集预测值与精确解的比较
Fig.5 Comparison of prediction training sets, prediction test sets and exact solutions of Euler equations
算例5 二维无黏Burgers方程
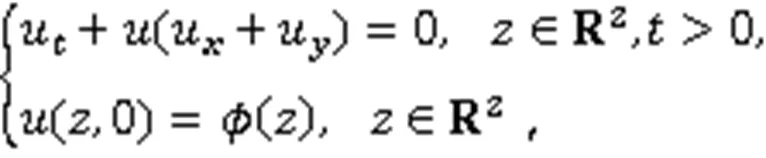
边界条件为
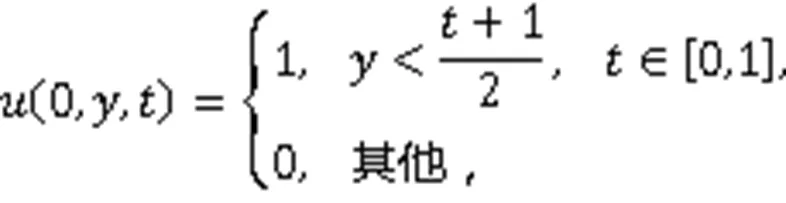
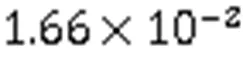

图6 二维无黏Burgers方程训练集、测试集预测值与精确解的比较
4 结论
受PINN启发,提出了一种求解双曲守恒律方程的改进的PINN算法。数值结果表明,经过多次训练,本文方法可用于求解双曲型方程静态激波问题、由连续状态发展为的激波问题、多波形问题、二维多激波问题。此外发现,在网络中加入正则化项不能提高网络的性能,有时反而令结果更糟,随机与非随机取样训练集与测试集均不影响效果。如何提高网络的精度以及如何将深度学习与双曲守恒律方程更好地结合,尚待进一步研究。
[1] LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. DOI:10.1006/jcph.1994.1187
[2] ISMAIL F, ROE P L. Affordable, entropy-consistent Euler flux functions II: Entropy production at shocks[J]. Journal of Computational Physics, 2009, 228(15): 5410-5436. DOI:10.1016/j.jcp. 2009.04.021
[3] 王令,郑素佩. 基于移动网格的熵稳定格式求解浅水波方程[J]. 水动力学研究与进展(A辑), 2020, 35(2): 188-193. DOI:10.16076/j.cnki.cjhd.2020. 02.006
WANG L, ZHENG S P. Solving shallow water wave equation based on moving grid entropy stable scheme[J]. Chinese Journal of Hydrodynamics(A), 2020, 35(2): 188-193. DOI:10.16076/j.cnki.cjhd.2020.02.006
[4] 程晓晗,聂玉峰,蔡力,等. 基于移动网格的熵稳定格式[J]. 计算物理, 2017, 34(2): 175-182. DOI:10. 19596/j.cnki.1001-246x.2017.02.007
CHENG X H, NIE Y F, CAI L, et al. Entropy stable scheme based on moving meshes for hyperbolic conservation laws[J]. Chinese Journal of Computational Physics, 2017, 34(2): 175-182. DOI:10.19596/j.cnki.1001-246x.2017.02.007
[5] TANG H Z, TANG T. Adaptive mesh methods for one- and two-dimensional hyperbolic conservation laws[J]. SIAM Journal on Numerical Analysis,2003,41(2): 487-515. DOI:10.1137/S003614290138437X
[6] HAN J Q, ARNULF J, E W N. Solving high-dimensional partial differential equations using deep learning[J]. Proceedings of the National Academy of Sciences, 2018, 115(34): 8505-8510. DOI:10. 1073/pnas.1718942115
[7] SIRIGNANO J, SPILIOPOULOS K. DGM: A deep learning algorithm for solving partial differential equations[J]. Journal of Computational Physics, 2018, 375: 1339-1364. DOI:10.1016/j.jcp.2018. 08.029
[8] SUN L N, GAO H, PAN S W, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 361: 112732. DOI:10.1016/j.cma.2019. 112732
[9] 黄婕,张丰,杜震洪,等. 基于RNN-CNN集成深度学习模型的PM2.5小时浓度预测[J]. 浙江大学学报(理学版), 2019, 46(3): 370-379. DOI:10.3785/j.issn.1008-9497.2019.03.016
HUANG J, ZHANG F, DU Z H, et al. Hourly concentration prediction of PM2.5based on RNN-CNN ensemble deep learning model[J]. Journal of Zhejiang University(Science Edition), 2019, 46(3): 370-379. DOI:10.3785/j.issn.1008-9497. 2019.03.016
[10]HORNIK K, STINCHCOMBE M, WHITE H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks[J]. Neural Networks, 1990, 3(5): 551-560. DOI:10.1016/0893-6080(90)90005-6
[11]ALLAN P. Approximation theory of the MLP model in neural networks[J]. Acta Numerica, 1999, 8: 143-195. DOI:10.1017/S0962492900002919
[12]CHEN T, CHEN H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems[J]. IEEE Transactions on Neural Networks, 1995, 6(4): 911-917. DOI:10.1109/72.392253
[13]RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. DOI:10.1016/j.jcp.2018.10.045
[14]JAGTAP A D, KAWAGUCHI K, KARNIADAKIS G E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks[J]. Journal of Computational Physics, 2020, 404: 109136. DOI:10.1016/j.jcp.2019.109136
[15]LU L, MENG X H, MAO Z P, et al. DeepXDE: A deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228. DOI:10.1137/19M1274067
[16]MAO Z P, JAGTAP A D, KARNIADAKIS G E. Physics-informed neural networks for high-speed flows[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 112789. DOI:10. 1016/j.cma.2019.112789
[17]ROE P L. Affordable,entrope-consisted,Euler flux function (with application to the carbuncle phenomenon)[C]// Proceedings of 11th International Conference on Hyperbolic Problems: Theory, Numerics, Applications. Lyon: Springe, 2006.
PINN-type algorithm for shock capturing of hyperbolic equations
ZHENG Supei, JIN Fang, FENG Jianhu, LIN Yunyun
,,710064,)
The numerical solution of hyperbolic equation is a well-know hot topic in the field of numerical solution of partial differential equation, among which the discontinuous capturing of hyperbolic equation is always a difficult problem. Inspired by physical-informed neural networks (PINN), this paper presents a PINN-type algorithm to approximately solve discontinuity problem of hyperbolic equations. It takes the data set constructed by coordinate as the input of neural network. The loss function in PINN algorithm is converted to the error between the output value of the training network and the reference solution (entropy compatible format data based on the fine grid) or the exact solution. Then the loss function is minimized by network optimization to obtain the optimal network parameters. Finally, some numerical examples are demonstrated to verify the feasibility of the proposed algorithm. The numerical results show that the proposed algorithm can capture shock waves, and it has high resolution, without nonphysical oscillations.
hyperbolic conservation laws equation; network prediction; PINN; shock capturing
O 241.8
A
1008⁃9497(2023)01⁃056⁃07
2021⁃11⁃12.
国家自然科学基金资助项目(11971075);陕西省自然科学基金青年项目(2020JQ-338,2020JQ-342).
郑素佩(1978—),ORCID:https://orcid.org/0000- 0003-2502-6998,女,博士,副教授,主要从事微分方程数值算法研究.
通信作者,ORCID:https://orcid.org/0000-0002-4387-5445,E-mail:jinfang53@163.com.


