Static Analysis of Anisotropic Doubly-Curved Shell Subjected to Concentrated Loads Employing Higher Order Layer-Wise Theories

Francesco Tornabene,Matteo Viscoti and Rossana Dimitri

Department of Innovation Engineering,School of Engineering,University of Salento,Lecce,73100,Italy

ABSTRACT In the present manuscript,a Layer-Wise(LW)generalized model is proposed for the linear static analysis of doublycurved shells constrained with general boundary conditions under the influence of concentrated and surface loads.The unknown field variable is modelled employing polynomials of various orders,each of them defined within each layer of the structure.As a particular case of the LW model,an Equivalent Single Layer(ESL)formulation is derived too.Different approaches are outlined for the assessment of external forces,as well as for non-conventional constraints.The doubly-curved shell is composed by superimposed generally anisotropic laminae,each of them characterized by an arbitrary orientation.The fundamental governing equations are derived starting from an orthogonal set of principal coordinates.Furthermore,generalized blending functions account for the distortion of the physical domain.The implementation of the fundamental governing equations is performed by means of the Generalized Differential Quadrature(GDQ)method,whereas the numerical integrations are computed employing the Generalized Integral Quadrature(GIQ)method.In the post-processing phase,an effective procedure is adopted for the reconstruction of stress and strain through-the-thickness distributions based on the exact fulfillment of three-dimensional equilibrium equations.A series of systematic investigations are performed in which the static response of structures with various curvatures and lamination schemes,calculated by the present methodology,have been successfully compared to those ones obtained from refined finite element three-dimensional simulations.Even though the present LW approach accounts for a two-dimensional assessment of the structural problem,it is capable of well predicting the three-dimensional response of structures with different characteristics,taking into account a reduced computational cost and pretending to be a valid alternative to widespread numerical implementations.

KEYWORDS Concentrated load; doubly-curved shells; generalized differential quadrature; laminated anisotropic materials;layer-wise theory;mapping technique

1 Introduction

Laminated materials are very often required in many engineering applications.In particular,an increasing need for structures with complex geometric shapes characterized by smart non-conventional fabrics is much more evident [1–4].In this way,an optimization of the material properties can be obtained from the model,since the lamination scheme can be selected according to the structural needs,especially when the geometry cannot be varied due to architectural and functional requirements[5,6].On the other hand,the introduction of curvature provides an optimization of the stress distribution.Nevertheless,classical models can lead to erroneous predictions due to an unusual structural behaviour coming from the absence of material and geometric symmetry planes[7–10].In order to prevent the invalidation of the design process and exposing the final product to some safety risks,new simple but accurate methodologies should be developed.Furthermore,a proper mathematical modelling of complex appliances,embedding all the curvature effects and constitutive couplings,can be very cumbersome in its conception as well as computationally demanding,due to the huge number of variables occurring in the structural problem [11,12].Three-dimensional elasticity solutions are the most accurate approaches for the correct prediction of a structural response [13–15].However,in the case of anisotropic materials and complicated structural shapes,a closed-form solution can not be easily found.Therefore,a large numerical system should be developed with a significative number of Degrees of Freedom(DOFs).This is likely to come across several numerical issues like the computational stability.For this reason,simplified two-dimensional formulations have been developed throughout literature,so that the solution is found with a lower computational effort [16–20].In particular,two main approaches can be traced,namely the Equivalent Single Layer(ESL)and Layer-Wise (LW) formulations [21–24].According to ESL,the three-dimensional doubly-curved solid is reduced to a surface located in its middle thickness.In this way,a 2-manifold is derived with its geometric parameters describing the shape of the actual structure[25,26].Moreover,the field variable,as well as the primary and secondary ones,are reduced to the surface at issue.A key aspect of this approach is the homogenization of the stacking sequence so that a set of equivalent properties can be computed.In contrast,the two-dimensional LW implementations account for a displacement field expansion within each lamina,thus providing an accurate local description of all the mechanical quantities.Furthermore,compatibility conditions are developed between two adjacent laminae so that the consistency of the whole model is assessed [27,28].Within the LW approach,the accuracy of the solution may be increased if the order of the adopted interpolating polynomials gets higher,or equivalently if a generic lamina is divided in some virtual sub-layers following a local-global strategy,thus leading to sub-laminate formulations [29–36].As far as the displacement field assumption is concerned,classical approaches provide a linear through-the-thickness assumption of the unknown in-plane field variables,whereas a rigid behaviour is assumed in the out-of-plane directions.In this way,no stretching effects can be predicted,as well as the softcore behaviour of the lamination scheme[37].In addition,a smooth displacement field assumption does not fit the actual interlaminar deformation during the deflection of the structure.For this reason,a higher order axiomatic expression for the out-of-plane variable is crucial in both LW and ESL approaches,even though the latters should embed in themselves with the well-known zig-zag function in order to obtain accurate results[38–43].A milestone for the assessment of the kinematic field variable is its unified description[44,45],which incorporates both higher order theories and classical approaches like the First Order Shear Deformation Theory(FSDT)and the Third Order Shear Deformation Theory(TSDT),outlined in references[46,47].Since it allows the introduction of a generalized set of thickness functions in both in-plane and out-of-plane directions,polynomials,non-polynomials and trigonometric functions can be employed to this purpose [48–50],depending on the material properties and relative thickness of the laminae embedded in the structure.Moreover,it is possible to develop an advanced set of axiomatic thickness functions,whose expressions is obtained from the mechanical shear properties of the lamination scheme,leading to the so-called refined zig-zag theories[51–53].

The fundamental governing equations have been analytically solved only for simple geometries and lamination schemes,such as frames,plates,cylinders and spherical panel.On the other hand,only cross-ply orthotropic laminates can be adopted,otherwise no mathematical procedures are available at the moment for the solutions of such differential sets of equations.For this reason,in references[54,55] the ESL structural problem for structures with single and double curvatures accounting for a generally anisotropic lamination scheme is numerically developed by means of the Generalized Differential Quadrature (GDQ) method.We recall that such methodology discretizes directly the derivatives of a given function,thus allowing to solve the problem directly in the strong form,as it has been shown in references [56–60].Belonging to the class of spectral collocation methods,it embeds a series of numerical techniques like the gaussian quadrature and the classical differential quadrature [61,62],accounting for a rectangular computational grid.The accuracy of the method comes from the proper selection of a set of discrete points from the physical domain,as well as the computation of the quadrature coefficients.In references [63,64] its accuracy has been compared to other numerical techniques.Moreover,it has been shown that it is a very reliable procedure for the analysis of lattice three-dimensional cells[65–67],as well as Functionally Graded Materials(FGMs)employing a reduced computational cost[68–71].Moving from the above discussed GDQ procedure,the Generalized Integral Quadrature (GIQ) method turns out to be an effective strategy for the numerical implementation of integrals with a domain collocation strategy.In references [72,73],the interested reader can find an extended treatise on the topic.

In classical variational approaches like the well-known Finite Element Method (FEM),an axiomatic set of shape functions are provided,leading to a weak form of the governing equations[74–76].However,this methodology induces some drawbacks in the solution due to the discrepancy between the geometry and the adopted interpolating function.As a matter of fact,this problem can be overcome if a domain is discretized with a fine mesh,which in turn increases the computational cost.In contrast,the Iso-Geometric Approach (IGA) adopts the actual geometry of the structure employed in the Computer Aided Design(CAD)procedure itself for the assessment of the unknown field variable of the governing equations.Starting from the pioneer works reported in reference[77],the IGA methodology has been successfully applied to several structural problems related to arbitrary shapes [78,79].It has been shown that IGA is a very efficient methodology in the case of structures of arbitrary geometries,especially when a significative domain distortion is required.In particular,the best performances of such methodology are reached when Non-Uniform Rational Basis Spline(NURBS) curves with higher order basis functions are adopted because they show a significative computational stability.In references [80,81],the curves at issue are presented in a comprehensive way,together with an iterative procedure for their computation.Furthermore,in references[82–83],a meshfree Galerkin method is applied for the buckling analysis of shallow shells with single and double curvatures accounting for geometric interpolation functions for the assessment of the unknown field variable.In reference[84],the meshfree approach has been adopted for the finite rotation analysis of structures with different curvatures.

Another topic related to the analysis of shell structures relies on the computation of concentrated loads within the structural problem.In classic domain decomposition procedures like FEM,generalized forces are applied at a specific node of the domain mesh [85,86].If the load is not applied in a computational point,a set of equivalent forces are derived by means of an interpolating procedure employing the adopted shape functions.The same approach can be found in references[87,88]where the GDQ algorithm has been adopted within each element in which the domain has been divided.As a consequence,a concentrated force pretends to be a boundary condition within the differential model.On the other hand,in the case of a problem developed within a single domain,in references[89–91],an interesting procedure based on GDQ and GIQ methods accounts for a differential-integral implementation on a rectangular plate under a concentrated load,taking into account the main features of the well-known Dirac-Delta function[92].On the other hand,a concentrated load can be seen as a particular case of a surface pressure acting on a very small area.Nevertheless,the distribution governing parameters should be set according to the actual dimension of the structure object of analysis[93,94].

In the present manuscript,a LW formulation is derived for the static analysis of generally anisotropic shell structures with a double curvature under the action of concentrated loads.The unknown displacement field variable is described,within each layer,employing a generalized approach with different higher order thickness functions.Furthermore,the displacement compatibility conditions between two adjacent layers are fulfilled.The geometry of the shell is described with curvilinear principal coordinates and a mapping procedure is adopted for arbitrarily-shaped structures.A generally anisotropic elastic behaviour is considered within each lamina.The fundamental set of differential equations is derived following an energy approach,together with the kinematic and static boundary conditions by means of a strong formulation of the structural problem.Then,non-conventional external constraints are enforced within the two-dimensional model.The differential problem is tackled numerically with the GDQ method,accounting for the discretization of the derivatives of a generic order,whereas integrals are solved with the GIQ numerical algorithm.Since the numerical model embeds in itself a smooth variation of derivatives,both surface distributed and concentrated loads are modelled with a comprehensive set of bivariate distributions,whose governing parameters have been carefully calibrated.Furthermore,the Dirac-Delta function is adopted in its classical and generalized GDQ discrete version for the assessment of concentrated loads[95–97].The main elements of novelty of the proposed method are the efficient numerical implementation of the concentrated load,which is a singularity among surface tractions,directly in the continuum model.Furthermore,the normalization of the distribution with respect to the surface area provides an effective calibration of the shape and position parameters.In the post-processing stage,an effective reconstruction of physical quantities throughout the entire shell thickness is assessed based on the three-dimensional static balance equations for a laminated anisotropic solid applied to each layer of the stacking sequence.A significative number of numerical investigations have been attached to the manuscript.The accuracy of the numerical predictions has been checked with respect to refined three-dimensional Finite Element models developed with a commercial package,showing a very good agreement between different approaches.Moreover,the inconsistency of higher order ESL formulations has been outlined for very thick structures characterized by very complex lamination schemes with a huge number of laminae with various material syngonies.Then,the solution has been checked for both single and double curvatures.The proposed higher order LW formulation has been added to the Differential Quadrature for Mechanics of Anisotropic Shells,Plates,Arches and Beams(DiQuMASPAB)project[98],a free research software which provides the static and the dynamic response of doubly-curved shell structures with various ESL and LW theories.

2 Doubly-Curved Shell Geometry

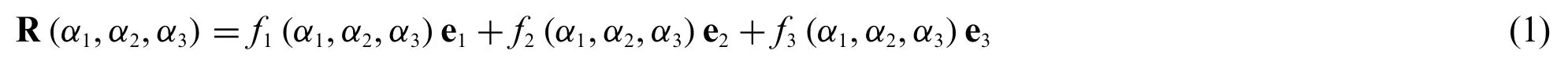
A doubly-curved shell is a three-dimensional solid within the Euclidean space (Fig.1).For this reason,if e1,e2,e3are the unit vectors of a global coordinate system,the position vector R(α1,α2,α3)of an arbitrary point of the structure can be described in terms of the following relation[21]:wheref1,f2,f3are functions of the variablesα1,α2,α3.It should be said that Eq.(1)assumes a physical meaning if the variations≤αi≤fori= 1,2,3 are declared,being,the extremes of the variation intervals.If a laminated structure composed byllaminae is considered,the overall thickness of the structurehcan be computed as the sum of the widthshkof each layer,withk=1,...,l:

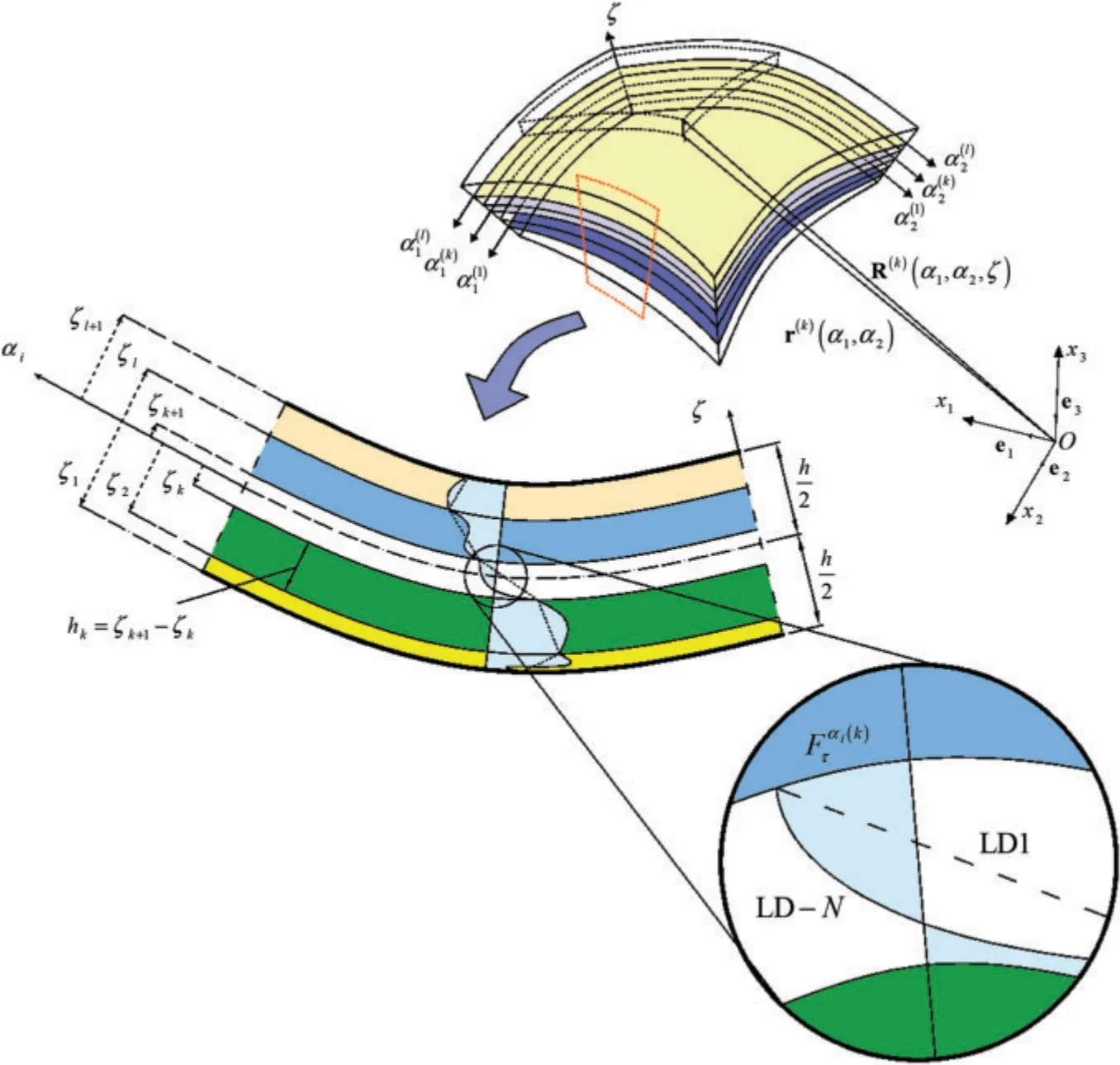
Figure 1:Geometric assessment of a doubly-curved shell according to a LW approach.Representation of a generic thickness function of different orders defined in each k-th layer of the stacking sequence for k=1,...,l,being l the total number of laminae occurring in the lamination scheme

As a matter of fact,the associationα3=ζis performed so that the axis at issue is oriented alongside the thickness direction of the shell.Moreover,a reference surface r(α1,α2)is assessed,located in the middle thickness of the structure,whose parametric directionsα1,α2are defined from the principal geometric features of the shell.Referring to a generick-th layer of a laminated structure,a unit vector setis introduced fork=1,...,l.On the other hand,ifhkassumes a constant value throughout the entire structure,can be obtained from an affine transformation alongsideζdirection ofα1,α2in-plane coordinates of the shell reference surface,thus setting=αifori=1,2.As a consequence,a key relation for the LW geometric and mechanic computation is introduced[24],defining the differential variation of local and global thickness coordinatesζ(k)andζ:

In this way,a reference surface r(k)(α1,α2)is defined in the middle thickness of eachk-th layer of the stacking sequence starting from the global geometric quantity r(α1,α2)referred to the global curvilinear coordinateO′α1α2ζaccording to the following expression[21],as shown in Fig.1.

whereζk,ζk+1denote the extreme locations of thek-th layer along the shell thickness direction,whereas n(α1,α2)accounts for the normal unit vector of the reference surface r(α1,α2),defined as follows:

where r,i=∂r/∂αidenotes the partial derivative of the shell reference surface with respect to the already introduced principal directionαifori=1,2[21].Starting from Eq.(4),the thickness curvature parameterreferred to theαi=α1,α2principal direction is computed:

Furthermore,the Lamé parametersand the principal curvature radiiof the reference surface of thek-th layer can be computed as:

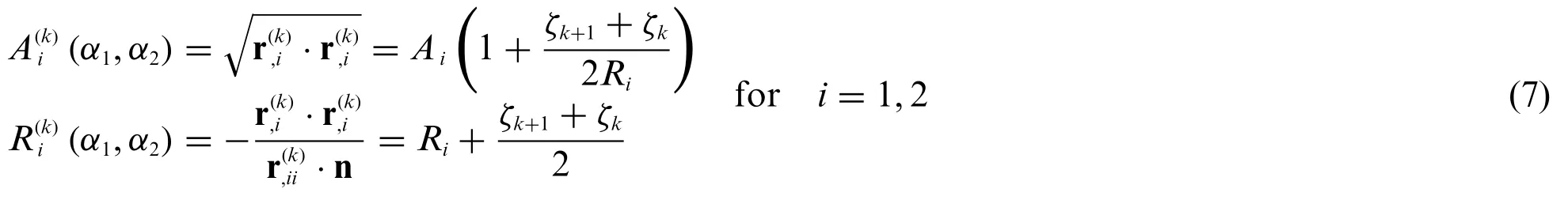
where n is the normal unit vector defined in Eq.(5),whereasaccount for the first and the second order derivative of Eq.(4)with respect toαi=α1,α2,respectively.In addition,Ai=Ai(α1,α2)andRi=Ri(α1,α2)fori= 1,2 are referred to the surface r(α1,α2)located in the middle thickness of the entire laminated structure.From the main outcomes of the differential geometry,such quantities are calculated according to the following expressions,setting[21]:

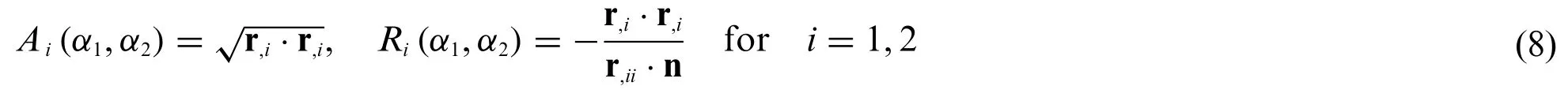
Having in mind all these premises,the three-dimensional position vector R(k)(α1,α2,ζ)of a generic point belonging to thek-th layer can be referred to r(α1,α2)as follows(Fig.1):

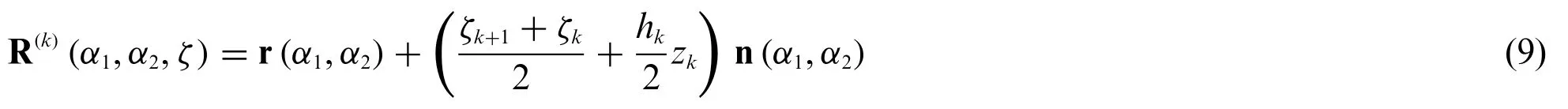
beingzk=2ζ(k)/hka dimensionless thickness coordinate belonging to the interval[-1,1].It is useful to compute the first order derivative ofzkwith respect to the local thickness coordinateζ(k),so that:

2.1 Arbitrarily-Shaped Shells

When the parametrization of the reference surface does not account for a curvilinear set of principal coordinates,the two-dimensional physical domain is distorted so that a rectangular dimensionless parent element is obtained,described in terms of the natural coordinatesξ1∈[-1,+1]andξ2∈[-1,+1],as it has been schematically shown in Fig.2.If we denote withthe location of thei-th corner of the distorted geometry,fori= 1,...,4,the blending functions presented in the following can be employed[21]:

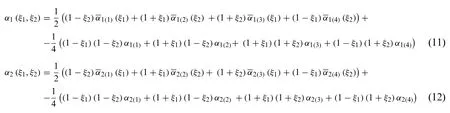
whereRi,p(u)is a rational B-Spline ofp-th order which can be computed from the following expression,beingwia proper weighting coefficient:

Setting for simplicity [a,b] = [0,1] and introducing a predefined knot vectora recursive relationship can be adopted to compute the B-Spline basis functionNi,p(u)ofp-th order.Starting withp=0,it is[21]:

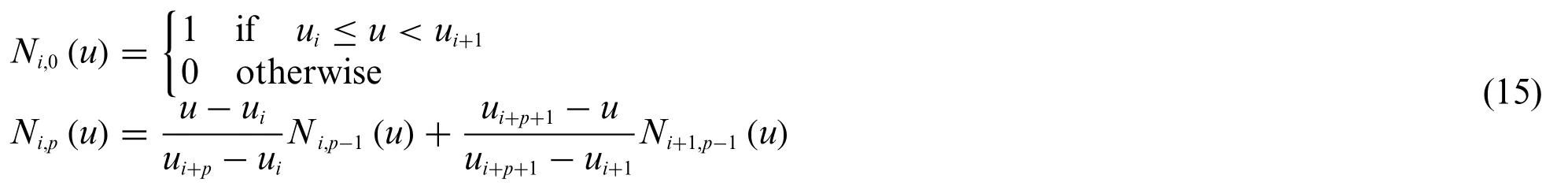
When arbitrarily-shaped structures are investigated,the fundamental relations,provided in terms of(α1,α2)∈should be expressed in terms ofξ1,ξ2coordinates within the interval [-1,1]×[-1,1].If we denote with J the Jacobian matrix of the coordinate transformationα1=α1(ξ1,ξ2),α2=α2(ξ1,ξ2),it can be stated that:

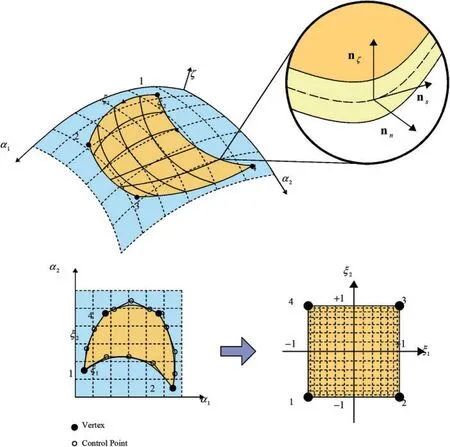
Figure 2:Isogeometric mapping of the physical domain employing NURBS curves.Definition of the local reference system along the edges of the distorted shell for the assessment of boundary conditions.Derivation of the rectangular computational domain employing natural coordinates

Accordingly,an inversion of Eq.(16)can be performed if det(J)=ξ1,α1ξ2,α2-ξ1,α2ξ2,α1≠0,leading to the definition of the inverse Jacobian matrix J-1:

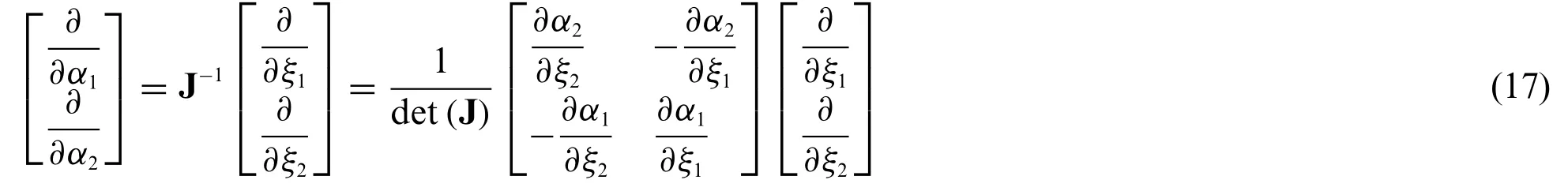
Once Eqs.(11) and (12) have been assessed,it is possible to provide an expression to define the first order partial derivatives with respect toα1,α2principal coordinates in terms of the natural onesξ1(α1,α2)andξ2(α1,α2),starting from the well-known derivation chain rule:

beingξi,αj=∂ξi/∂αjfori,j= 1,2.From a comparison of Eqs.(17)and(18),it is possible to provide the complete expression ofξi,αjcoefficients,leading to[21]:

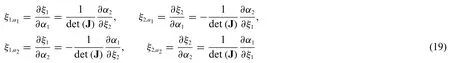
Based on Eq.(18),it is possible to express the second order derivatives with respect to the principal coordinateα1,α2in terms ofξ1,ξ2.One gets:

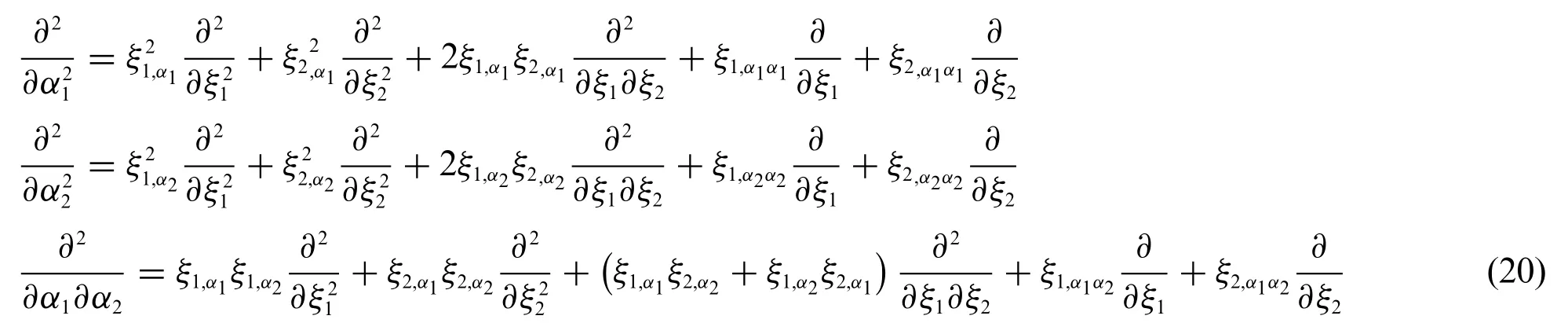
Eq.(20) assesses the dependence of the second order derivatives with respect toα1,α2in terms of the first and second order derivatives with respect toξ1,ξ2natural coordinates.Accordingly,the equation at issue is not bi-linear in the present formulation.In the following,the interested reader can find the complete expression of coefficients introduced in Eq.(20):

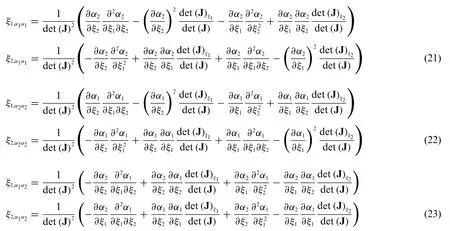
The first order derivatives det(J)ξ1,det(J)ξ2of the determinant det(J)of the Jacobian matrix introduced in Eq.(16)with respect toξ1andξ2,respectively,read as follows:

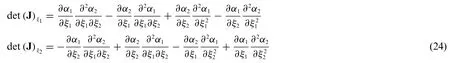
A useful nomenclature is now introduced,so that the edges of the physical domain can be univocally identified.Referring to the dimensionless rectangular parent element described in terms of the natural coordinatesξ1,ξ2,the following definitions[21]are outlined(Fig.2):

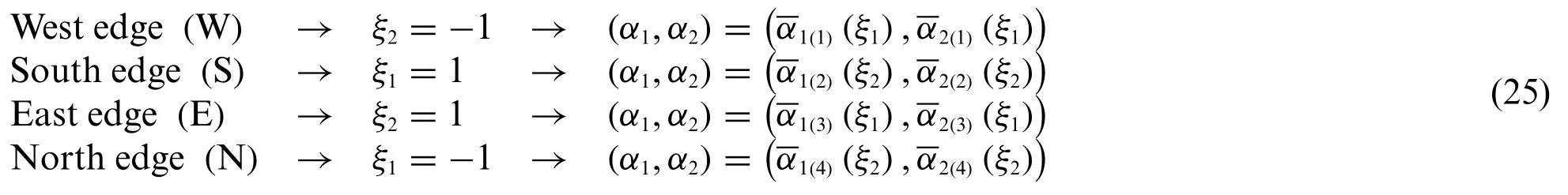
3 Unified Formulations for Kinematic Relations

In the present section a unified assessment of the kinematic field variable is presented following the LW methodology.Referring to a generick-th lamina of the laminate,each componentfori= 1,...,3 of the three-dimensional displacement field column vector U(k)α1,α2,ζ(k)can be expanded up to an arbitraryN-th order,thus introducing for eachτ=0,...,N+1 a generic functionfori=1,...,3 dependent from the local thickness coordinateζ(k)[24]:

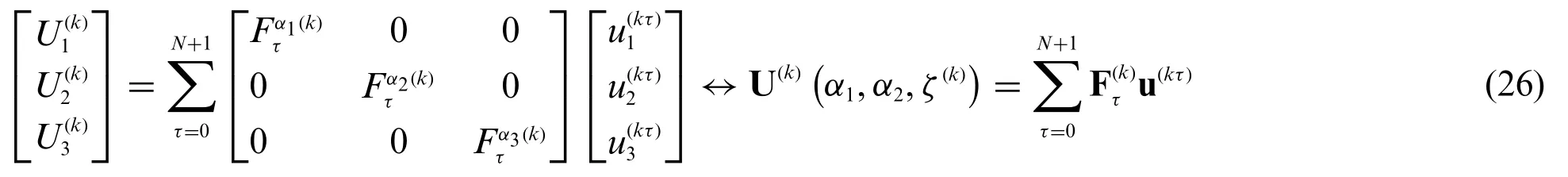
Since a laminated doubly-curved shell structure is considered withk= 1,...,l,wherelis the total number of superimposed laminae,the displacement field variable should fulfil the interlaminar compatibility conditions.To this purpose,an interpolation methodology based on higher order polynomials is followed for the definition offorτ=0,...,N+1.Accordingly,the dimensionless thickness coordinatezkintroduced in Eq.(9)is considered:

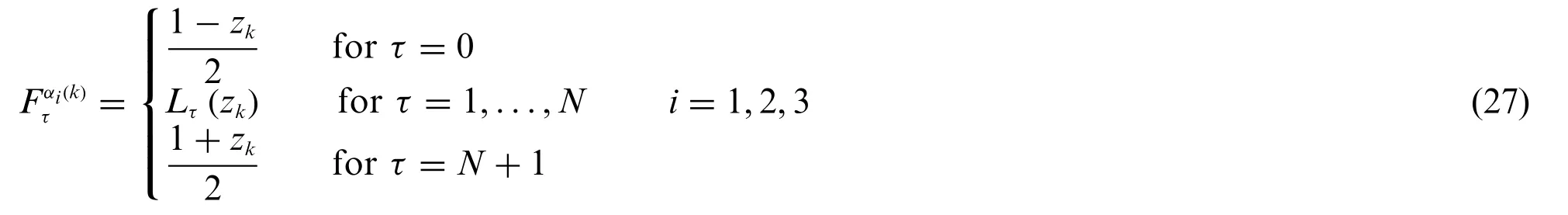
whereLτ(zk)forτ= 1,...,Nis defined employing various interpolating polynomials.As can be seen,Eq.(27) refers to the three-dimensional displacement distribution throughout the thickness.As a consequence,the interlaminar compatibility conditions are directly satisfied by the axiomatic assumptions of the unknown field variable itself.The first order derivative of the generalized thickness functions introduced in Eq.(27)with respect toζ(k)can be computed as:

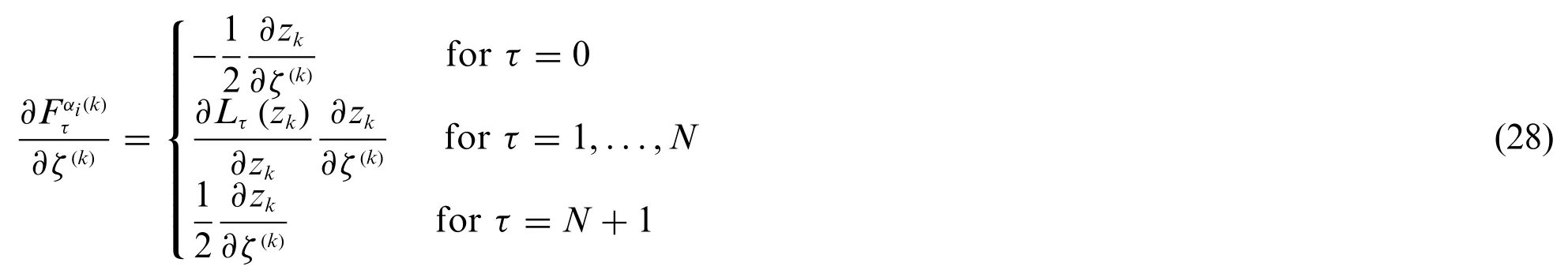
As can be seen,the derivatives∂zk/∂ζ(k)occurring in Eq.(28)are calculated according to Eq.(10).

If power functions are introduced in Eqs.(27) and (28),the following expressions should be adopted for eachτ=1,...,N[24]:

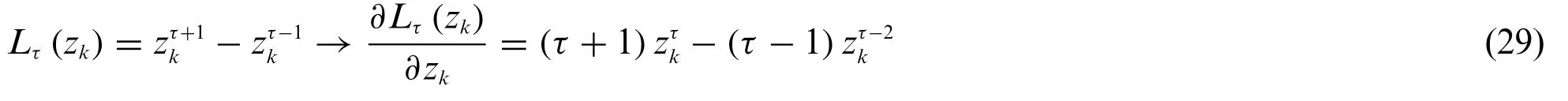
On the other hand,a formulation based on higher order Lagrange interpolating polynomials reads as follows:

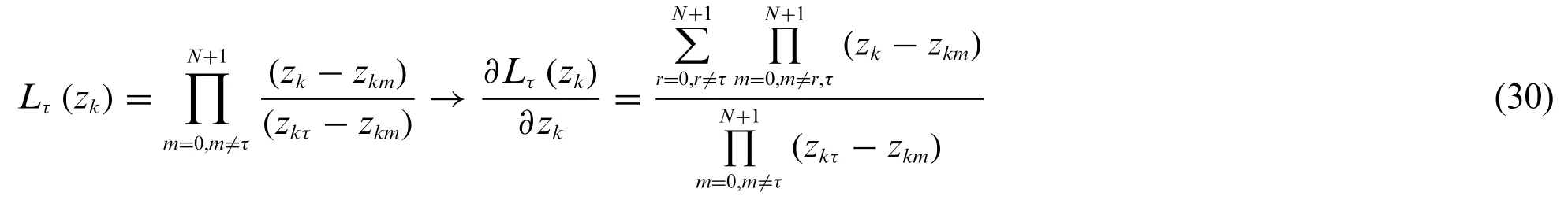
If trigonometric functions are adopted in Eq.(27),for eachτ=1,...,Nreads as:

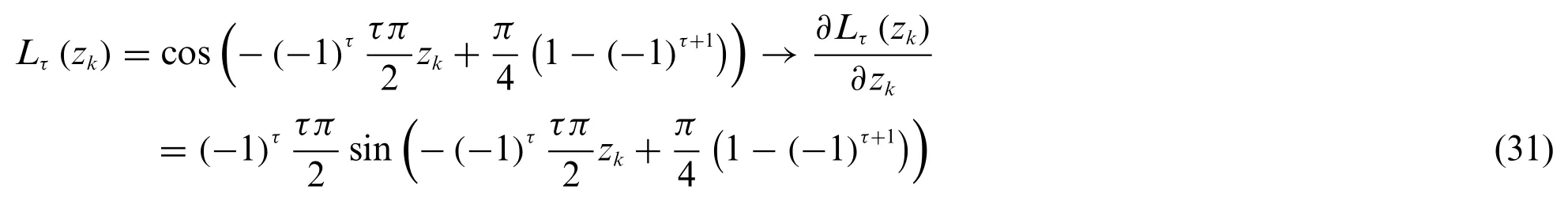
Furthermore,the Jacobi orthogonal polynomialscan be employed to define the LW thickness functionforτ=1,...,N,leading to:

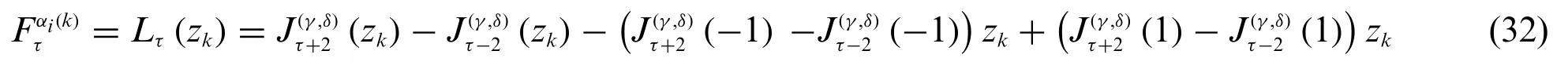
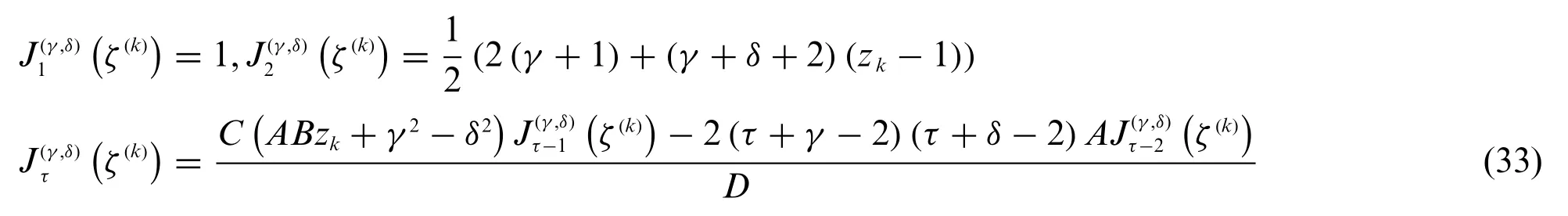
settingA=2τ+γ+δ-2,B=A-2,C=A-1 andD=2(τ-1)(τ+γ+δ-1)B.Accordingly,the first order derivative ofLτ(zk)of Eq.(32)with respect toζ(k)occurring in Eq.(28)can be computed as:

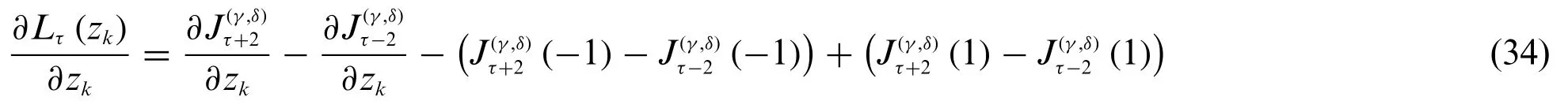
Based on a LW higher order approach(26),the kinematic relations are derived starting from those referred to the three-dimensional solid described in Eq.(9),which are briefly recalled for the sake of completeness:

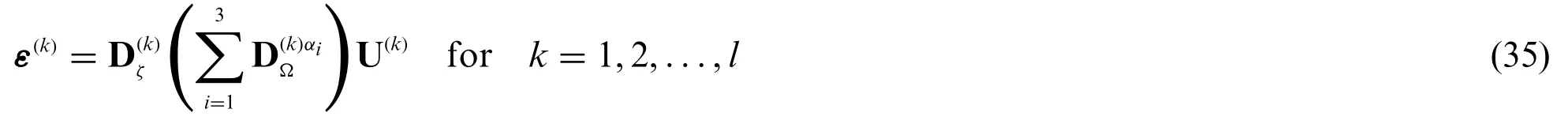
whereε(k)=are the three-dimensional strain vector referred to thek-th layer.Furthermore,the kinematic through-the-thickness differential operatoris defined as:

In Eq.(37)the differential vectorshave been introduced,whose extended version accounts as follows:

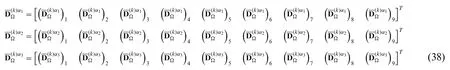
The kinematic relation of the three-dimensional solid reported in Eq.(35),can be arranged if the unified LW displacement field assessment of Eq.(26)is substituted,leading to the introduction of the

LW generalized strain vectorε(kτ)αi(α1,α2)=defined for eachτ=0,...,N+1 andαi=α1,α2,α3[24]:

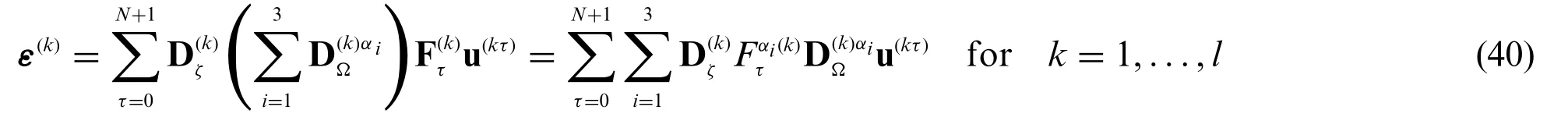
It is useful to introduce,for eachαi=α1,α2,α3,the vector Z(kτ)αireferred to theτ-th kinematic expansion order,settingτ=0,...,N+1:

Eventually,Eq.(40)turns into:

4 Anisotropic Constitutive LW Relations

We now focus on the elastic constitutive behaviour of a generic doubly-curved laminated structure.Thus,eachk-th layer of the stacking sequence,fork= 1,...,l,is modelled by means of a three-dimensional relationship valid for generally anisotropic materials.In this perspective,a local reference system denoted withis derived from the direct application of the Neumann’s Principle to the periodic unit volume of each lamina.As a matter of fact,such material axes are intended to be featured so that one axis is parallel to the shell outward normal direction,namely(k)=ζ.If we denote withfori,j= 1,...,6 the generic stiffness constant linking thei-th component of the three-dimensional stress vector(k)=referred to the material reference system to the correspondingj-th element of the three-dimensional strain vector(k)=,the generally anisotropic behaviour of thek-th layer can be expressed as[21]:

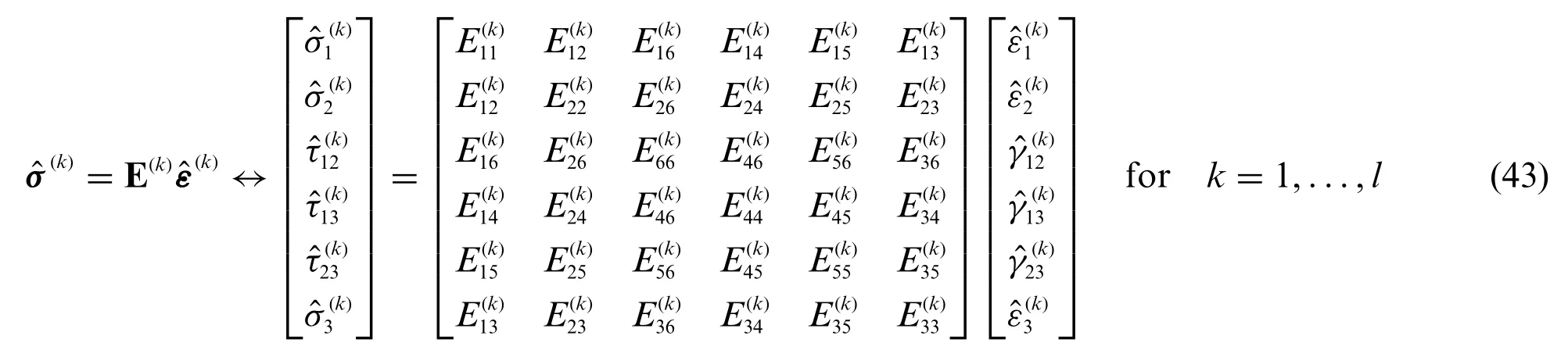
A key aspect of the present LW formulation is the assessment of all the fundamental governing relations into the geometric reference system of each layer oriented alongside the reference surface principal directions.To this purpose,an angleϑkis identified in eachk-th layer accounting for the deviation betweenandα1material and geometric directions,respectively.If we denote with T(k)(ϑk)the rotation orthogonal matrix referred to each lamina of the structure,the constitutive relationship of Eq.(43)can be rotated with the following linear transformation so that it is referred to the geometric coordinate axesO′α1α2ζof the reference surface of the structure thus leading to the rotated stiffness matrixfor eachk= 1,...,l,whose generic component is denoted withfori,j=1,..,6:

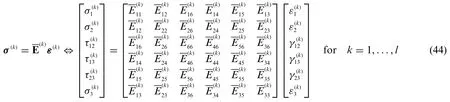
beingσ(k)=the three-dimensional stress and strain vectors,respectively,referred to the shell geometric reference system.Referring to the anisotropic stiffness matrix E(k)occurring in Eq.(43),it usually consists in the three-dimensional elastic coefficientsfori,j= 1,...,6.In plane stress conditionswithin the twodimensional model in Eq.(43),the reduced elastic coefficientsare adopted.In particular,they are derived from a correction of the three-dimensional stiffness matrix,as follows:

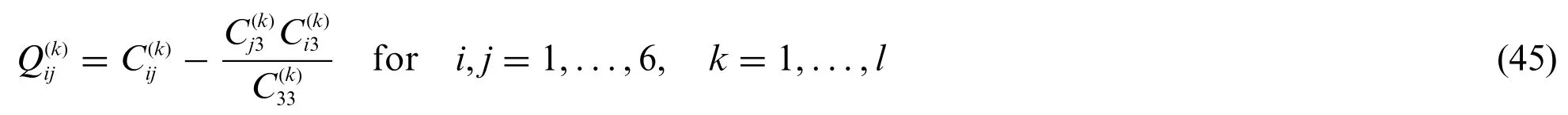
It should be remarked that the constitutive relationship of Eq.(44),expressed for eachk-th layer,has a three-dimensional connotation.As a matter of fact,it should be reduced to the local reference surface introduced in Eq.(4).From the computation of the variationδ Φkof the elastic strain energy of the doubly-curved solid for eachk=1,...,l,one gets[21]:

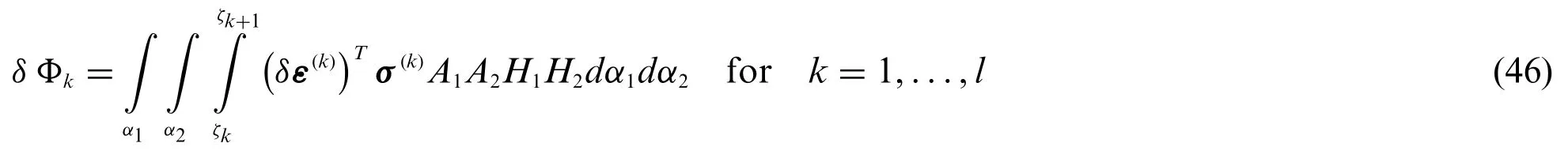
Introducing in the previous relation the unified assessment of the displacement field variable of Eq.(26)and the LW kinematic relation of Eq.(42),for eachτ-th kinematic expansion order withτ= 0,...,N+ 1 the generalized stress resultant vector S(kτ)αi(α1,α2)=is introduced,withα=α,α,α:i123

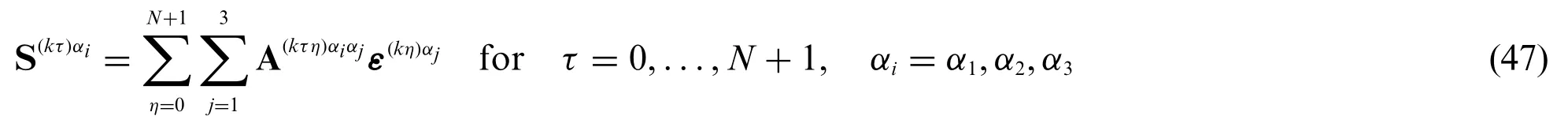
being A(kτη)αiαjthe generalized constitutive operator,computed for eachτ,η= 0,...,N+1 andαi=α1,α2,α3according to the following definition:

In a more expanded form,A(kτη)αiαjmatrix introduced in the previous equation reads,for eachk-th layer,as:

setting sub-matrices A(kτη)[00]αiαj,A(kτη)[01]αiαj,A(kτη)[10]αiα j,A(kτη)[11]αiαjas follows:

The generic component of Eqs.(50)–(53)are obtained from a through-the-thickness homogenization of the mechanical properties of eachk-th lamina according to the following expression,settingand[21]:

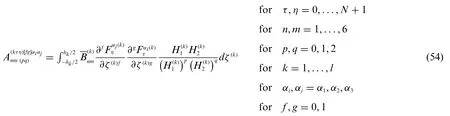
In the previous relation,coefficientis defined so thatfor eachn,m= 1,..,6.Accordingly,if the LW definition of the displacement field of Eq.(26)accounts for a constant out-ofplane displacement field assumption,such quantity should be corrected by means of the well-known shear correction factorκ(ζ)=5/6,namely:

Referring to a genericτ= 0,...,N+1 andαi=α1,α2,α3,it is possible to express the higher order LW constitutive relationship of Eq.(47) in terms of the generalized displacement field vector u(kη)=introduced in Eq.(26)for each reference surface of thek-th layer,taking into account the kinematic relation(40):

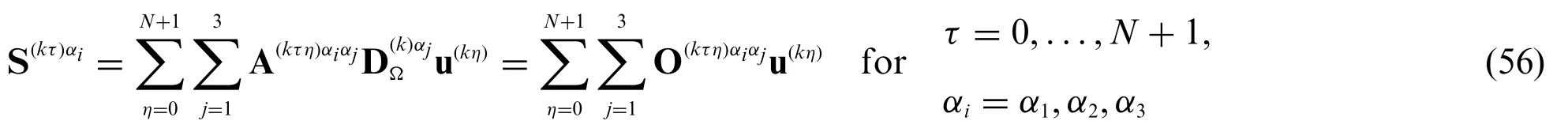
In Appendix A,an extended version of the components of the previously-introduced matrix O(kτη)αiαjcan be found.It will be seen that the present version of the generalized elastic law is a key for the definition of both static and kinematic boundary conditions within the higher order LW framework.

5 Governing Equations

In the present section the fundamental relations of the static problem for a laminated doublycurved structure are derived in the LW framework employing a higher order displacement field assumption.In particular,an energy approach will be followed,accounting for the curvature effects of the geometry.A generalized methodology is proposed for the assessment of surface loads acting on the structure,and an effective solution is provided for the implementation of concentrated loads.A consistent form of the fundamental governing equations is provided,together with the natural and non-conventional boundary conditions,characterized by three-dimensional capabilities.

5.1 External Loads

The present LW formulation considers a two-dimensional structural assessment for each layer of the laminated structure.Accordingly,a generick-th lamina of constant thicknesshk,withk=1,...,l,is intended to be loaded at its intradosby the static loadsalongα1,α2,α3principal directions,whereas the tractionsare applied at the extrados.For the sake of conciseness,the vectoris introduced.Thus,its components assume the following general form so that a general load caseφ(k±)(α1,α2)can be assigned to the structure[21]:

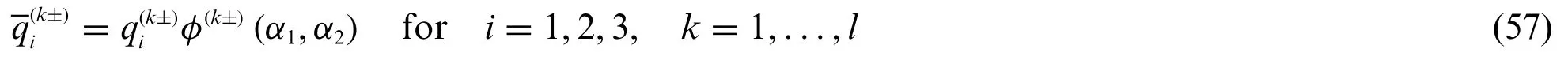
Accordingly,if a uniform load is applied to the arbitraryk-th lamina,Eq.(57) is computed so that:

In addition,a Gaussian function has been implemented in the two-dimensional model,settingthe position parameters,＞0 the variances of the bivariate distribution and∈[-1,1]the correlation factor:

Furthermore,a Super-Elliptic shape of surface loads is introduced so thatare the shape factors of the distribution of power coefficientn(k),whereasassume the role of position parameters andβ(k)accounts for the orientation of the principal axes with dispersion:

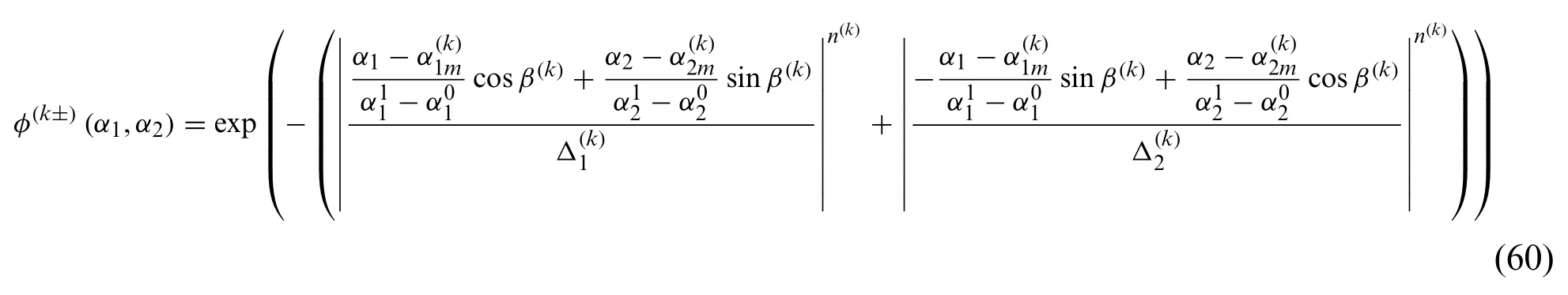
As a matter of fact,forn(k)= 2,Eq.(60)provides the well-known elliptic distribution.A general surface loading can be modelled also by means of a bivariate Fourier series in whichterms are assigned to theα1andα2direction,so that:

If the Jacobi polynomialsof governing parametersγ(k),δ(k)are employed for the assessment of general loads within eachk-th lamina,the bivariate load distribution of Eq.(57)assumes the following form,settingk=1,...,l:

with,fori=1,2,reading as:

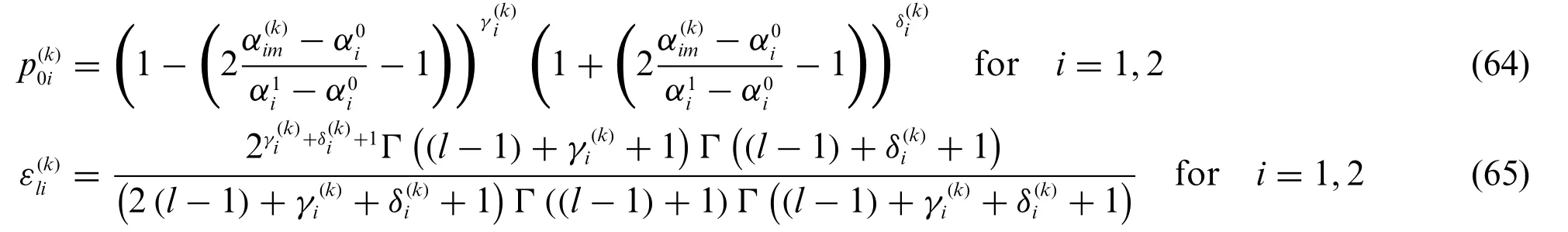
Following the approach outlined in Eq.(57),a concentrated load can be embedded within the two-dimensional LW formulation by properly setting a load distribution.Let us consider for a generick-th layer a concentrated load vectorof magnitudeQ(k+)applied atζ(k)= +hk/2 and a vectorreferred to the layer bottom surface located atζ(k)= -hk/2 of magnitudeQ(k-).For the sake of conciseness,we will adopt the compact notationAccordingly,the deviation of the vector at issue fromα1,α2,ζshell principal directions is identified by means of the anglesrespectively.As a matter of fact,each componentQ(k±)iof Q(k±),is derived as follows[21]:

Thus,an equivalent surface tractionis provided for eachi=1,2,3,defining the effects of the concentrated load components of Eq.(66):

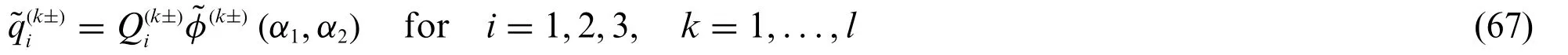
The surface tractions of Eq.(67)are conveniently arranged in the vectorGenerally speaking,the bivariate function(α1,α2)occurring in the previous equation consists of the well-known Dirac-Delta functionδ,namely:

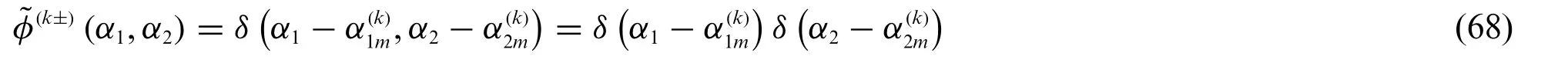
The function at issue has a singularity foraccounting for the following properties:

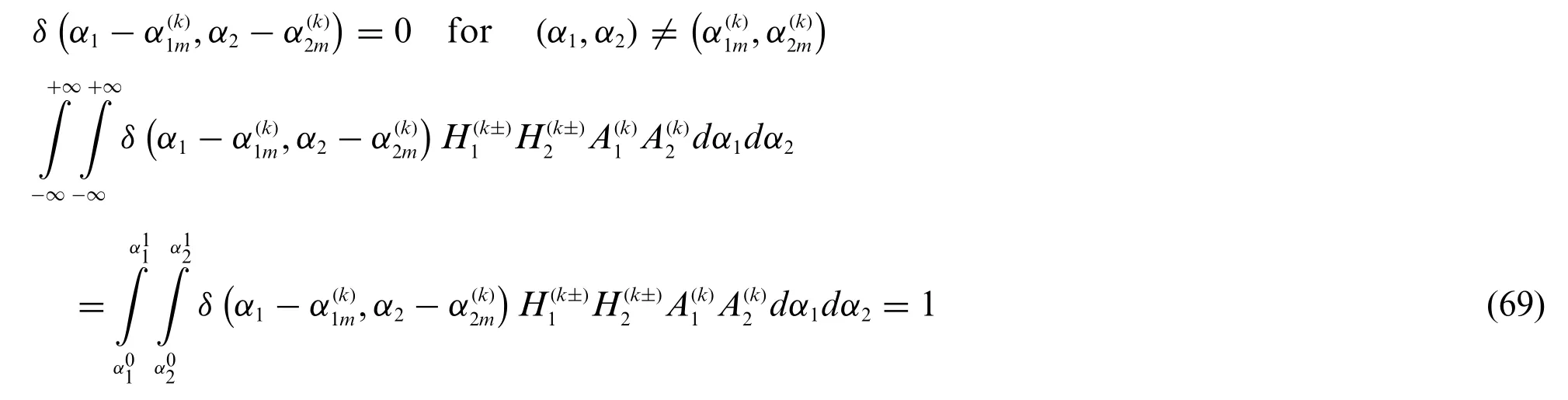
On the other hand,the numerical modelling of theδfunction in the continuum smooth model can be quite difficult because no closed-form analytical expressions can be provided in Eq.(69).As a consequence,the physical meaning of concentrated load could be not properly interpreted.For this reason,the concentrated load is modelled as a particular case of surface load according to Eq.(57),as here applied to a very small area.Furthermore,the distribution is normalized with respect to the area of the extrados or intrados of the shell so that it perfectly fulfils the main properties of the Dirac-Delta function in Eq.(69).

When an arbitrary bivariate distributionφ(k±)(α1,α2)is selected for the description of a concentrated load among those reported in Eqs.(58)–(62),the following relation should be considered:

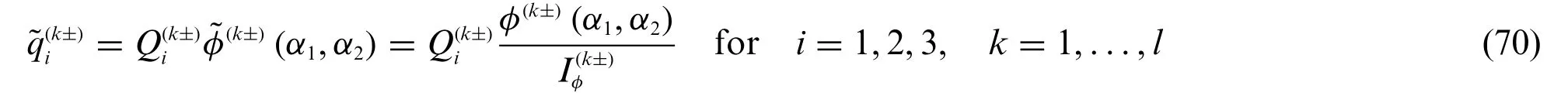
wheredenotes the surface integral ofφ(k±)(α1,α2)performed on the top(+)or bottom(-)surface of thek-th layer calculated by means of the rectangular domain

In this way,the surface integral of(α1,α2)distribution employed in Eq.(67) fits the main features of the Dirac-Delta function already outlined in Eq.(69),thus giving:

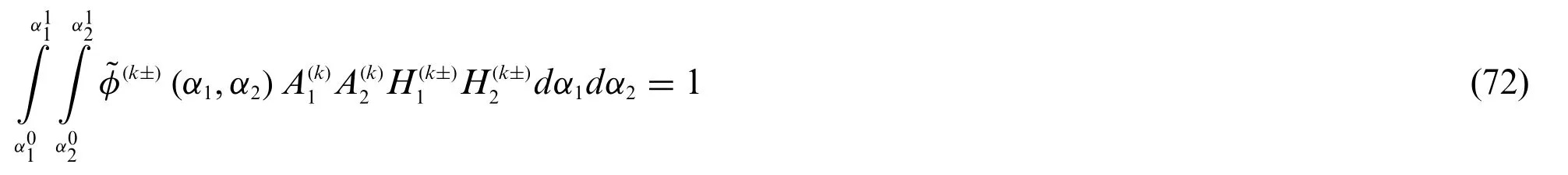
In other words,Eq.(72)requires that the resultant of the corresponding pressure associated to the concentrated load should be equal to the three-dimensional applied vector Q(k±)in all its components.A surface pressureis introduced for eachαi=α1,α2,α3principal direction,consisting in a contribution referred to the generally-shaped loadassessed in Eq.(57)and the vectorembedding the effects of concentrated loads:

Since a higher order displacement field assumption has been considered according to Eq.(26)in each layer of the structure,the Static Equivalence Principle is applied so that the computation of the virtual work associated to the vectorsgets into the derivation of a generalized surface load vectordefined within the reference surface of all the layers of the stacking sequence fork=1,...,l.One gets:

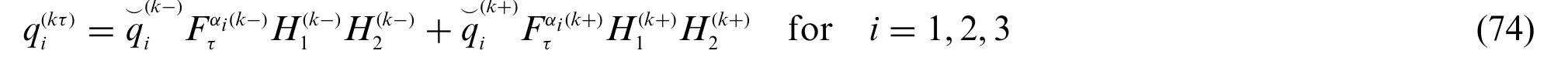
In the previous equation,refers to the computation of the thickness functionat the top and bottom,respectively,of thek-th layer.In the same way,the main curvature parametersandare introduced within the generic lamina.As a matter of fact,in all the simulations reported in the present manuscript,a perfect bonding between two adjacent laminae is assumed,therefore the structure can be loaded,according to Eq.(74),only at its top and bottom surfaces,located atζ=+h/2 andζ=-h/2,respectively.

5.2 Fundamental Relations

We now account for the energy procedure employing the well-known Minimum Potential Energy Principle [21] for the determination of the static response of the structure under the action of static loads.According to the LW approach,a stationary configuration of the potential energyΠof the shell is computed,taking into account the variation of the total elastic strain energyδΦ and virtual external workδ Le:

Integrating by parts,the following equilibrium relations are derived in terms of S(kτ)α iand q(kτ),reading as[21]:

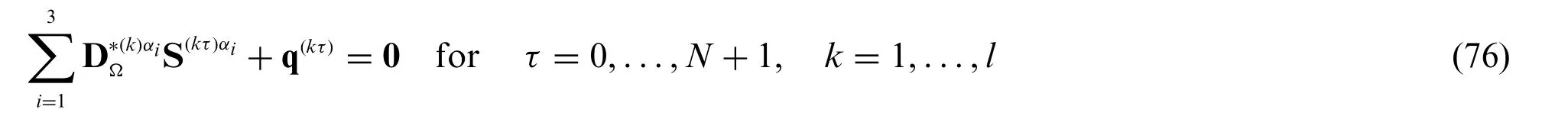
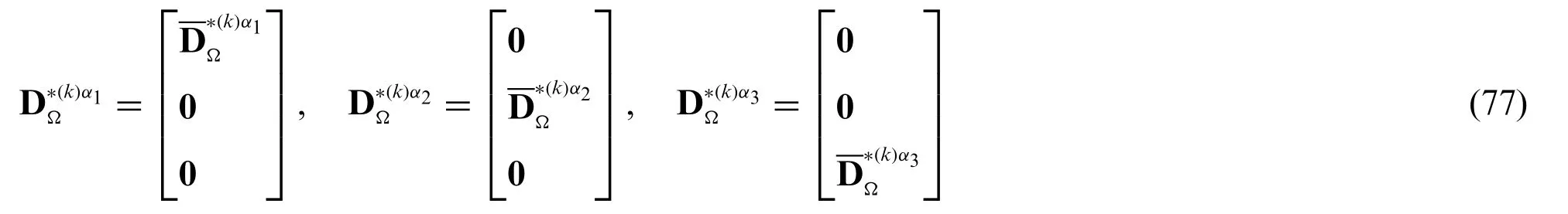
setting the following definitions:

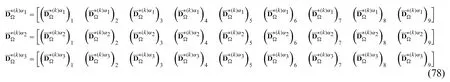
An extended version of the components of the vectors introduced in Eq.(78) has been now reported:

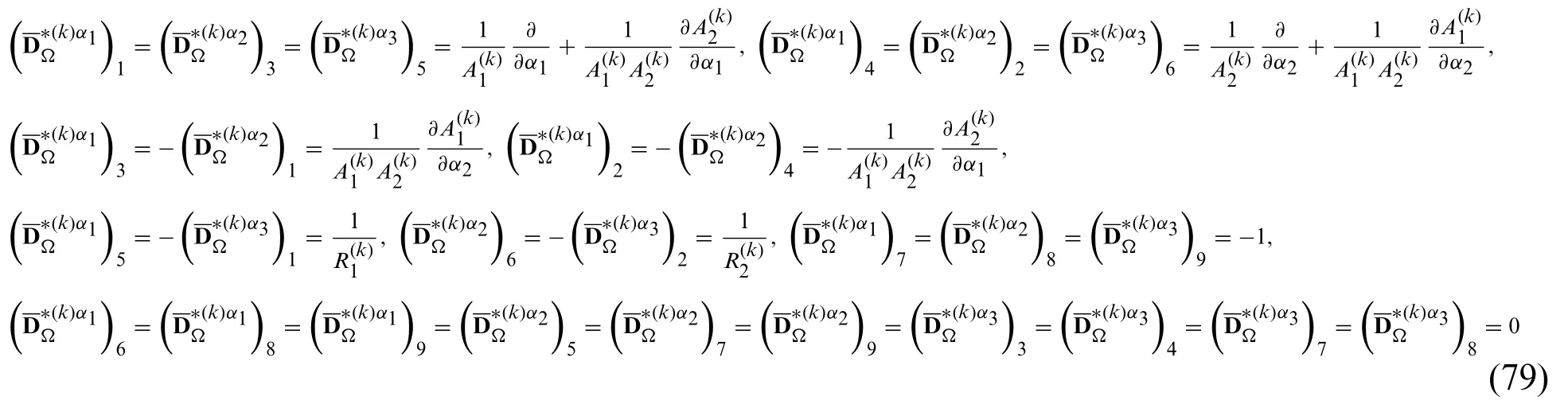
The fundamental relations for the static assessment of an anisotropic doubly-curved shell in terms of generalized displacement componentsare easily derived from Eq.(76)combined with Eq.(42)and(47),leading to an expression referred to a genericτ-th kinematic expansion order[21]:

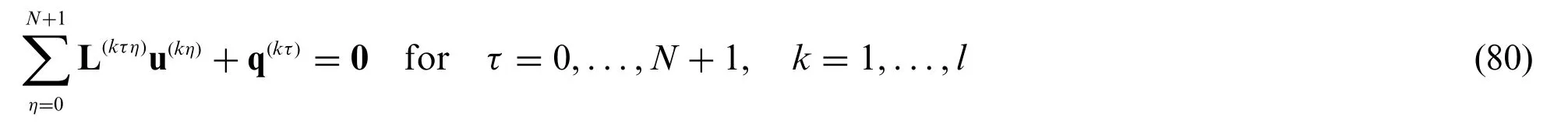
where the fundamental operator L(kτη)is defined for eachτ,η-th in a generick-th layer withk=1,...,las follows:

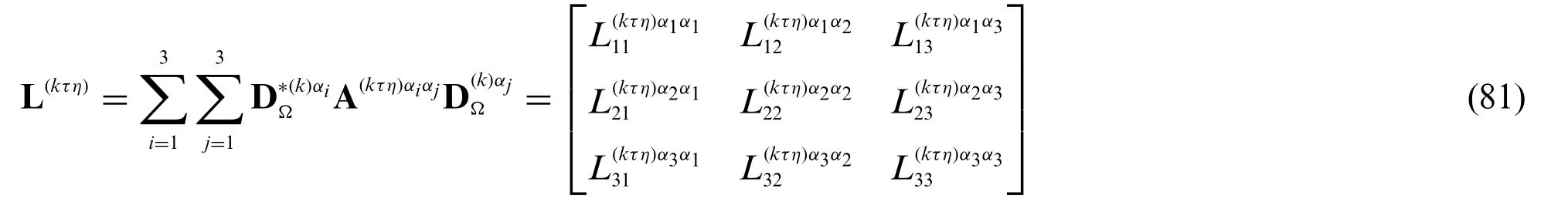
The complete expression ofwithτ,η= 0,...,N+1 andi,j= 1,2,3 can be found in Appendix B.

Starting from the physical interpretation of the kinematic variables introduced in Eq.(27),it should be recalled that the generalized displacement field vectors corresponding toτ= 0 andτ=N+1 are defined in such a way that the compatibility conditions that should be enforced between two adjacent layers are implicitly enforced,namely:

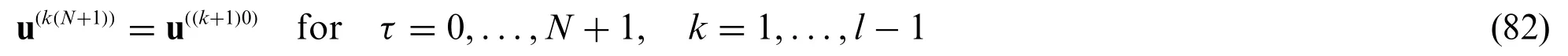
being u(k(N+1))and u((k+1)0)the generalized displacement field vectors associated to the extrados and intrados of thek-th and the(k+1)-th layer,respectively.Furthermore,Eq.(80)is assembled so that all the expansion orders of the kinematic assumption in Eq.(26)are considered,leading to the final fundamental relation:

Note that the interlaminar compatibility conditions of Eq.(82)are modelled in Eq.(83)by means of the identity matrix I located in the proper position of the fundamental operator.In this way,an independent equation is added for eachk-th layer so that the generalized displacement field associated toτ=0 is the same to the(k+1)-th lamina,referred to a kinematic expansion orderτ=N+1.

From the present energy formulation it is also possible to derive the conventional external constraints associated to the boundaries of the physical domain.If a generalized displacement field component is assigned within eachk-th layer of the laminate,the following relations should be enforced at the shell edges[21]:

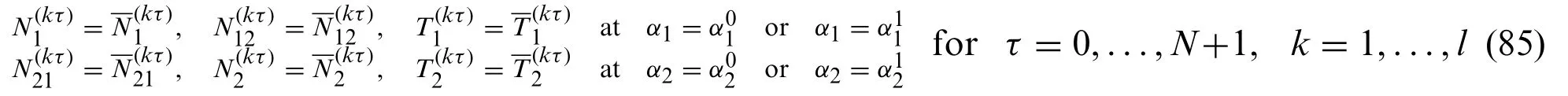
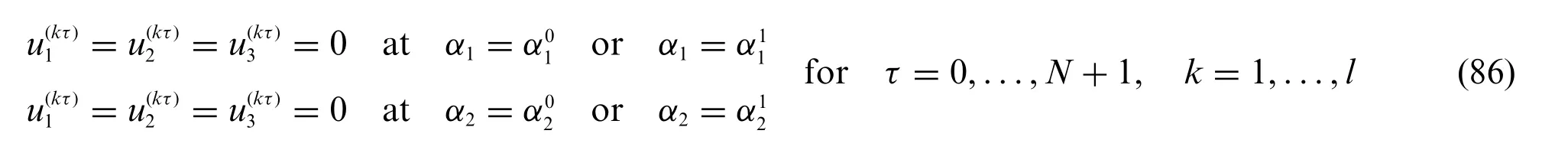
In a similar way,the free(F)edge boundary condition moves from Eq.(85)as follows:

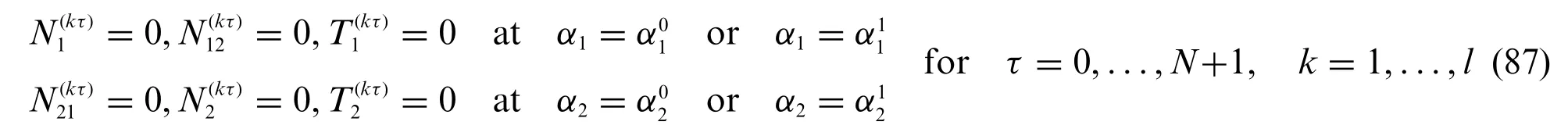
Referring to Eq.(85),the generalized stress resultants employed for the assessment of boundary conditions are enforced if the components of a boundary stress vectorare applied at the edges of the structure.Accordingly,is intended to be obtained from the sum of a prescribed stress vectorand a vector=dependent from the three-dimensional displacement field vector U(k)=

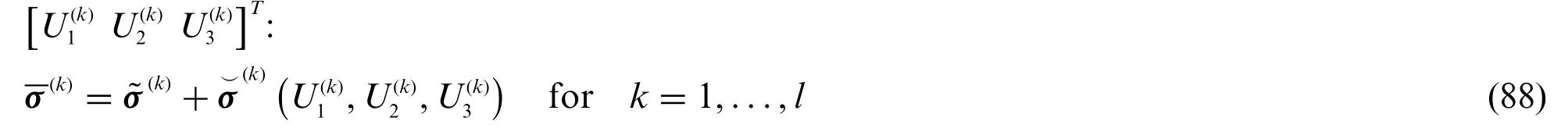
Referring to the shell sides located atα1=αs1fors=0,1 within the physical domain,the following definitions can be outlined in eachk-th layer of the stacking sequence[21]:

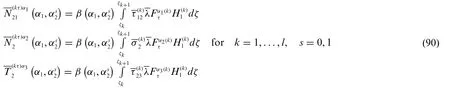
Furthermore,a parabolic stress distribution accounts for a polynomial expression ofλ:

Starting from Eqs.(89)and(90),a generalized set of non-conventional boundary conditions and prescribed stresses is developed if general in-plane univariate distributionsandwiths= 0,1,are associated to the components of the applied stresses vectorfork= 1,...,l.Tothis purpose,a dimensionless coordinateξrwithr= 1,2is introduced within the closed interval[0,1]for a smart assessment of general boundary conditions,namely:

In the case of constant in-plane distribution of stresses,the relationβs(αr)= 1 forr= 1,2 is assumed.Furthermore,two different analytical univariate expressions forhave been provided.A Double–Weibull(W)distribution accounts as follows:

By the way,based on Eqs.(89)and(90)a set of non-conventional constraints can be enforced to the model if the stress components ofare provided in each point of the three-dimensional shell edge by a series of linear elastic springs.Referring to the regions located atα1=α1sfors=0,1,it can be said that[21]:

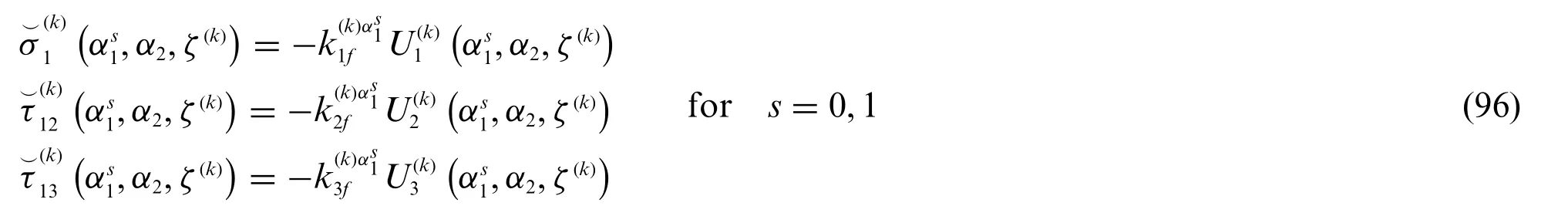
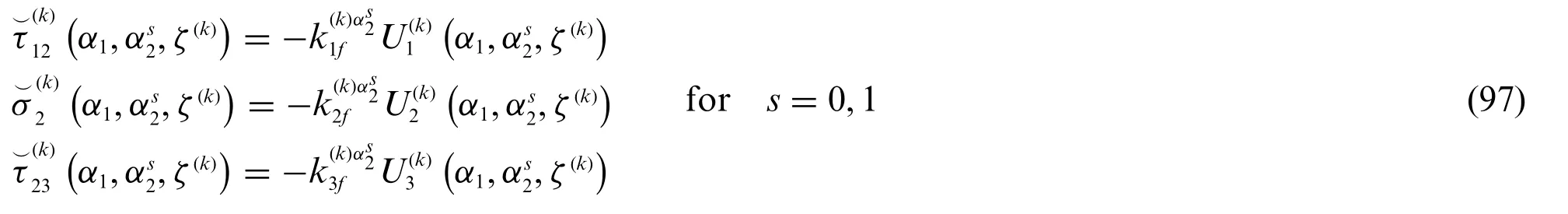
whereas Eq.(97)assumes the following form:

As a consequence,for eachτ-th kinematic expansion order withτ= 0,...,N+1,two different sets of generalized stress resultants are derived which are associated toandstress components,according to the following definitions:

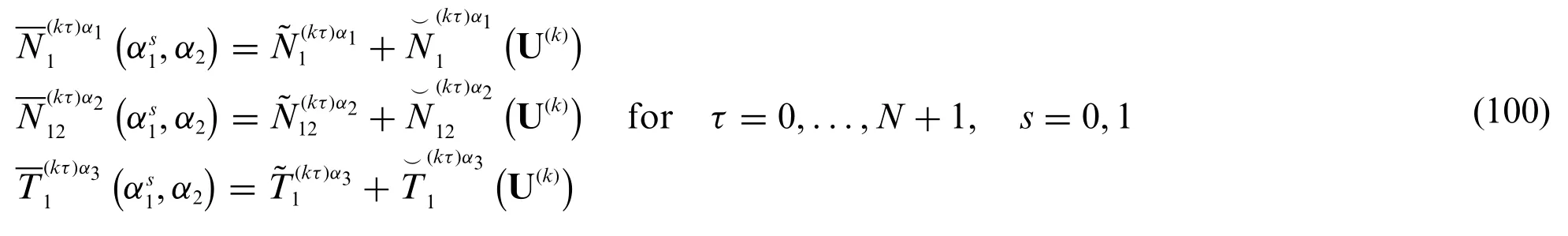
The generalized boundary stress resultants acting atα2=fors=0,1 read as follows:

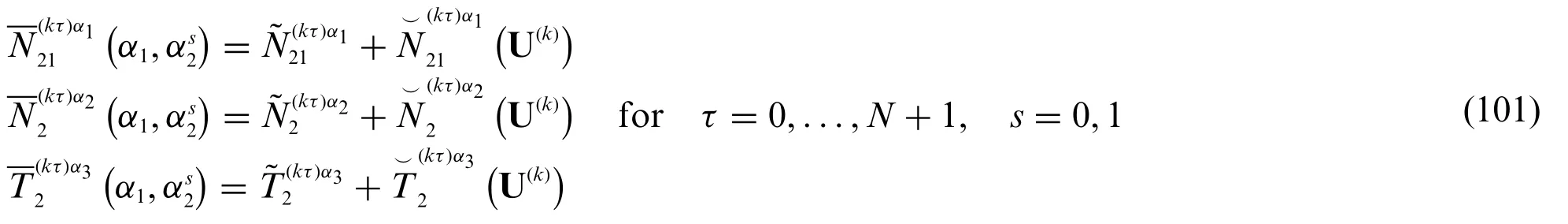
Referring to Eq.(100),the contribution coming from the applied stresses and linear springs can be arranged in the following compact matrix form:

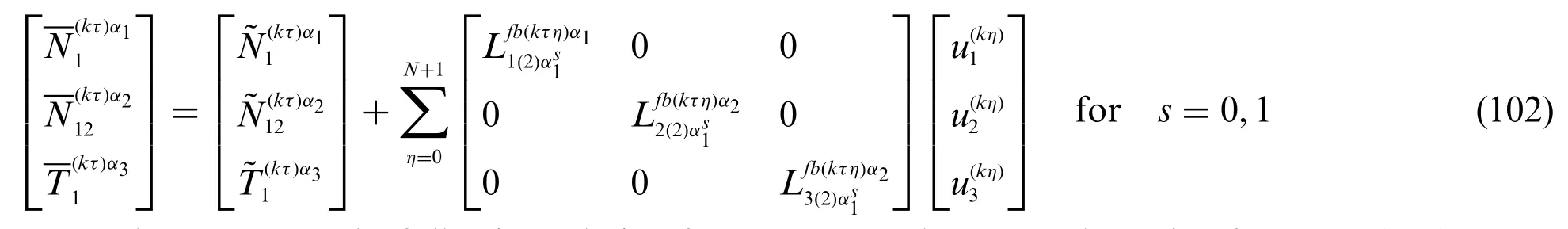
In the same way,the following relation forα2=can be assessed starting from Eq.(101):

Fundamental coefficientsoccurring in Eqs.(102) and (103) are computed for eachk-th layer andτ,η=0,...,N+1,according to the following effective expression:

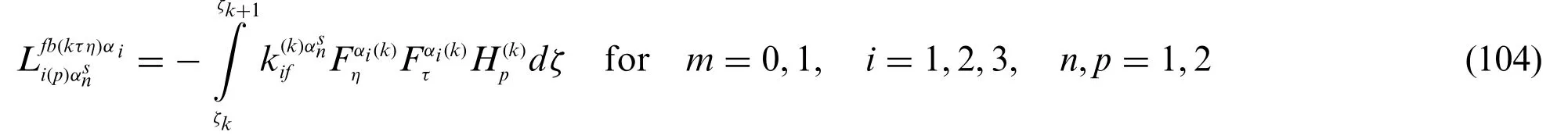
In the case of arbitrarily-shaped domains,the application of the blending functions of Eqs.(11)and(12)requires a rearrangement of natural boundary conditions assessed in Eqs.(86)and(87).To this purpose,a right-handed reference system is introduced from the geometric properties of a generic curve lying on the r(α1,α2)reference surface.The corresponding unit vectors,denoted with nn,nsand nζ,read as[21]:

wherenrifori= 1,2,3 and withr=n,s,ζare the components of the vectors at issue with respect to the shell geometric reference systemO′α1α2ζ.In particular,since nrwithr=n,s,ζstands for the local principal directions of an arbitrary curve belonging to the reference surface r(α1,α2),it should be said thatnn3=ns3=nζ1=nζ2= 0 andnζ3= 1.Referring to a particularτ-th kinematic expansion order,forτ= 0,...,N+1,the generalized displacement field vector u(τ)can be expressed with respect to such coordinate system according to the following transformation relation:

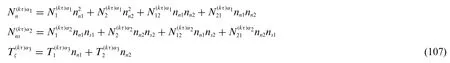
For prescribed displacementsor stressesalongside the edges of an arbitrarily-shaped shell,the mechanical and kinematic constraints reported in the following are derived from the minimum potential energy principle[21]:

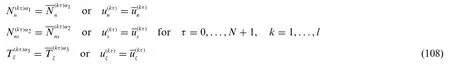
6 Equivalent Single Layer Theory

In the present manuscript a LW formulation is presented for laminated anisotropic doubly-curved shells.Since a generalized approach has been followed,the structure can be geometrically described in terms of r(α1,α2)referring to the global curvilinear coordinate systemO′α1,α2ζassessed in Eq.(1).As a consequence,the three-dimensional position vector can be expressed as[21]:

where r(α1,α2)is located in the middle thickness of the entire structure.The geometric Lamè parametersA1(α1,α2),A2(α1,α2),of the shell,as well as the main curvature radiiR1(α1,α2),R2(α1,α2),are thus calculated by means of Eq.(8).

As far as the unified formulation of the displacement field is concerned,a set of u(τ)generalized vectors forτ= 0,...,N+1 is defined on the reference surface r(α1,α2),thus turning Eq.(26)into the following one:

The thickness function matrix F(τ)is defined employing a power expansion for the displacement field.In the case of laminated structures,the Murakami’s function is adopted.For more details on the topic,the interested reader can refer to reference[24].For concentrated and surface loads within the ESL formulation,the generalized distributions of Eqs.(58)–(62) become independent from thek-th lamina.

7 Numerical Implementation with the GDQ Method

In the present section the LW model for anisotropic doubly-curved shells outlined in the manuscript is numerically tackled by means of the GDQ method.Belonging to the class of spectral collocation algorithms,the GDQ approach represents a quadrature procedure to discretize then-th order derivatives of an arbitrary function.Referring to a generic univariate functionf=f (x)withx∈[a,b],it gives[21]:

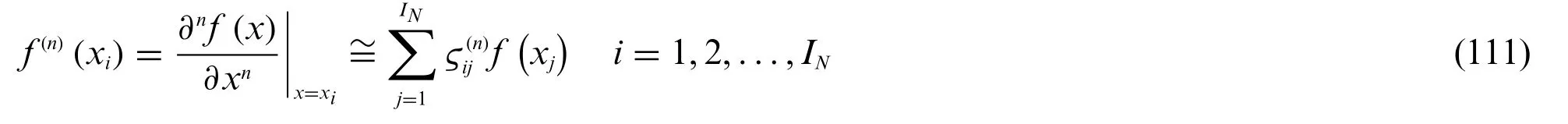
whereN ＞ndue to the consequences of the Weierstrass Interpolation Theorem.The weighting coefficients occurring in Eq.(111)are calculated from the following recursive procedure:

Accordingly,in the present manuscript the computational domain has been discretized inINandIMpoints alongα1,α2principal directions,respectively,according to the non-uniform Chebyshev-Gauss-Lobatto(CGL)harmonic distribution[21].Referring to a dimensionless domain[-1,1],the generic pointxiof the distribution withi=1,...IQis introduced so that:

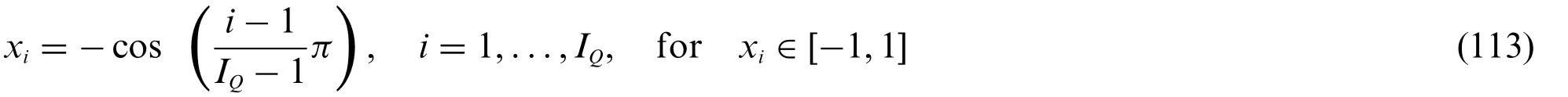
Starting from the GDQ rule in Eq.(111),the well-known GIQ method is assessed so that integrations restricted to a generic intervalof a univariate functionf=f (x)can be numerically tackled,settingxkdiscrete points,withk=1,...,l:

GIQ weighting coefficients=wjk-wikare computed following the procedure reported in reference [21].We now focus on the numerical assessment of the concentrated loads within the computational domain by means of the Dirac-Delta function according to what exerted in Eq.(69).Following the procedure suggested by references[90,91],the GDQ and GIQ rules are adopted for the implementation of the concentrated load in the present strong form problem according to Eq.(69),assuming that the vector at issue is applied in one of the selected discrete computational points.The GDQ algorithm of Eq.(111)for the discretization of the fundamental differential relations of Eq.(83)is adopted for all the internal discrete points of the computational domain,whereas the static and kinematic external constraints are numerically enforced at boundaries.Referring to the inner nodes of theIN×IMtwo-dimensional grid,it gives forr=2,...,IN-1 ands=2,...,IM-1:

where,are evaluated in each point of the computational grid according to Eq.(7),whereas the integral properties of the Dirac-Delta function of Eq.(69)are then adopted for the discretization of the fundamental governing equations in the computational point corresponding to that of the physical domain,denoted with,where the concentrated load has been applied according to Eq.(66).Some remarks are reported in references[85,90]for more details.

Furthermore,the Dirac-Delta function of Eq.(68) has been also implemented according to the generalized approach in reference[89].Moving from the methodology presented in Eq.(115),the concentrated load application pointcan be selected regardless the nature of the computational grid.In particular,a procedure based on the Lagrange interpolating Polynomials is followed so that the applied load is transferred to theIN×IMdiscrete set of point starting from an arbitrary location within the physical domain.One gets forr=2,...,IN-1 ands=2,...,IM-1[90]:

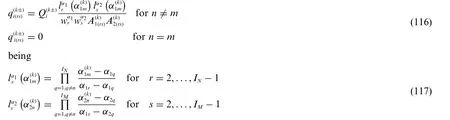
Once the fundamental differential problem outlined in Eq.(83)has been implemented by means of the GDQ method according to Eq.(111),the overcoming computational problem is efficiently solved by means of a proper condensation of the linear system.To this purpose,the unknown DOFs,embedded in the vectorδ,are arranged so thatδbandδdare referred to the boundary(“b”points)and the inner nodes(“d”points),respectively[21].One gets:

where fb,fdare the external load vectors associated to the“b”and“d”points,respectively.If Eq.(118)is expressed only in terms ofδdvector,the following reduced linear system is obtained:

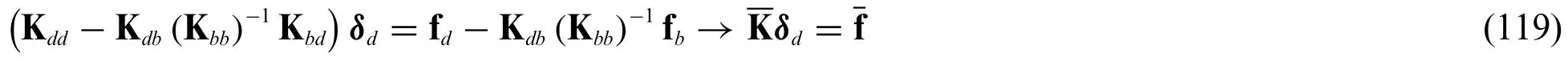
8 Post-Processing

The present formulation accounts the static structural assessment of laminated doubly-curved shell structures employing a two-dimensional formulation by LW approach.Since the solution is located at the middle surface of eachk-th layer,the higher order displacement field assumption of Eq.(26)can be adopted for the derivation of the three-dimensional response of the solid.On the other hand,the results may not fulfil the external tractions applied at the intrados and the extrados of each lamina.For this reason,a correction of stresses should be performed.

From the closed interval[-hk/2,hk/2],representing thek-th lamina thickness,a set ofITpoints is selected,whose generic onewithg= 1,...,ITis derived from the CGL harmonic distribution of Eq.(113).Then,the three-dimensional displacement field vector isevaluated in eachpoint of the three-dimensional solid,fori= 1,...,IN,j= 1,...,IMandg= 1,...,IT,employing the unified approach of Eq.(26):

In the same way,the discrete formof the threedimensional strain vector is calculated according to Eq.(35),settingi= 1,...,IN,j= 1,...,IMandg=1,...,IT:

Starting from the previous equation,it is possible to derive in the arbitrary point located atthe corresponding membrane stresses,for eachk-th layer,according to the elastic constitutive law of Eq.(44),leading to:

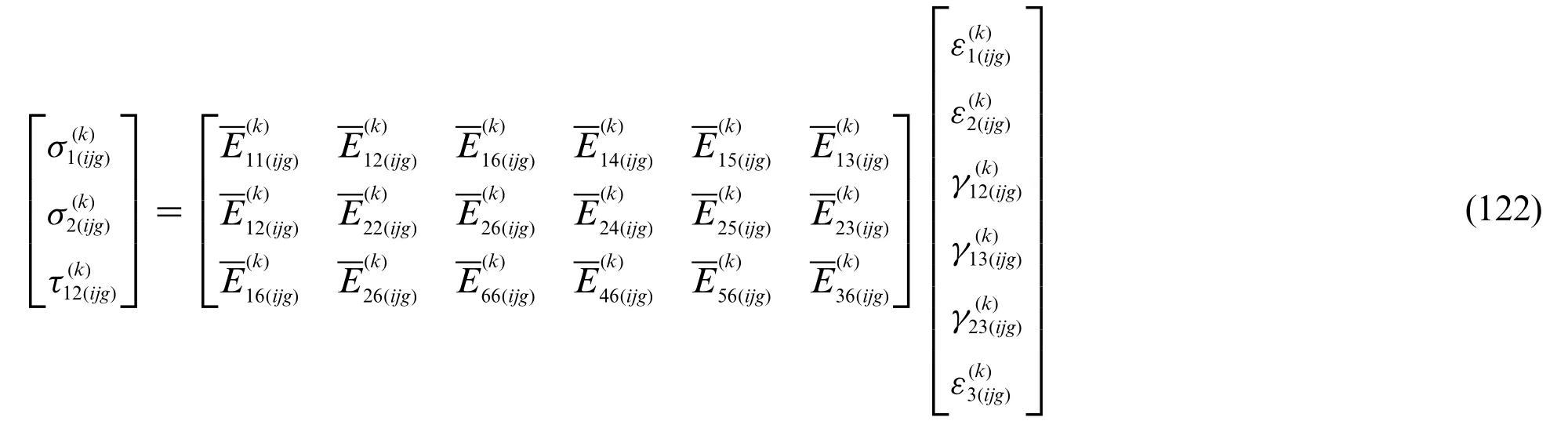
At this point,the three-dimensional equilibrium equations of a doubly-curved solid written in curvilinear principal coordinates should be recalled,remembering thatdζ=dζ(k):

witha(k),b(k),c(k)reading as:

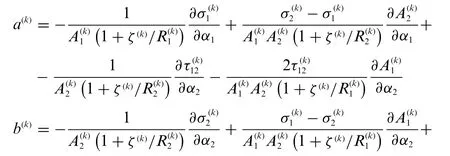
From the three-dimensional relations reported in Eq.(123),the out-of-plane stress componentsare derived for eachpoint,once the in-plane stresses are computed in Eq.(122),and their first order derivatives are calculated by means of the GDQ method of Eq.(111).Furthermore,two different loading conditions have been considered for eachk-th lamina,leading to prescribed values ofat the top and the bottom surfaces of the layer.Nevertheless,only the tractions referred toζ(k)=+hk/2 can be enforced.With particular reference to the first laminak=1,denote the in-plane components of the load vector already defined in Eq.(73) for eachapplied atζ(1)=-h1/2,one gets:

Since a perfect bonding has been considered at the interlaminar level,the following relations should be considered too:

The values of,shear stresses obtained from Eq.(123) can now be corrected so that the in-plane loading conditions referred to thel-th lamina are fulfilled,namelyandTo this end,two vectorsofIL=l·ITcomponents are introduced at eachpoint withi=1,...,INandj=1,...,IM,settings=k·g:

Each element of the vectors at issue can now be corrected so that out-of-plane shear stresses fulfil the in-plane loading conditions at the top surface of the shell[21]:

In the same way of what defined in Eq.(127),the vectorof normal stresses is introduced:

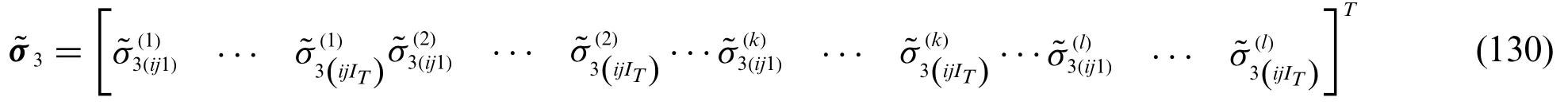
Furthermore,the out-of-plane three-dimensional strain components profile can now be adjusted employing the recovered distributions of out-of-plane stressesfors= 1,...,IL.The following relations are adopted for eachk-th layer:

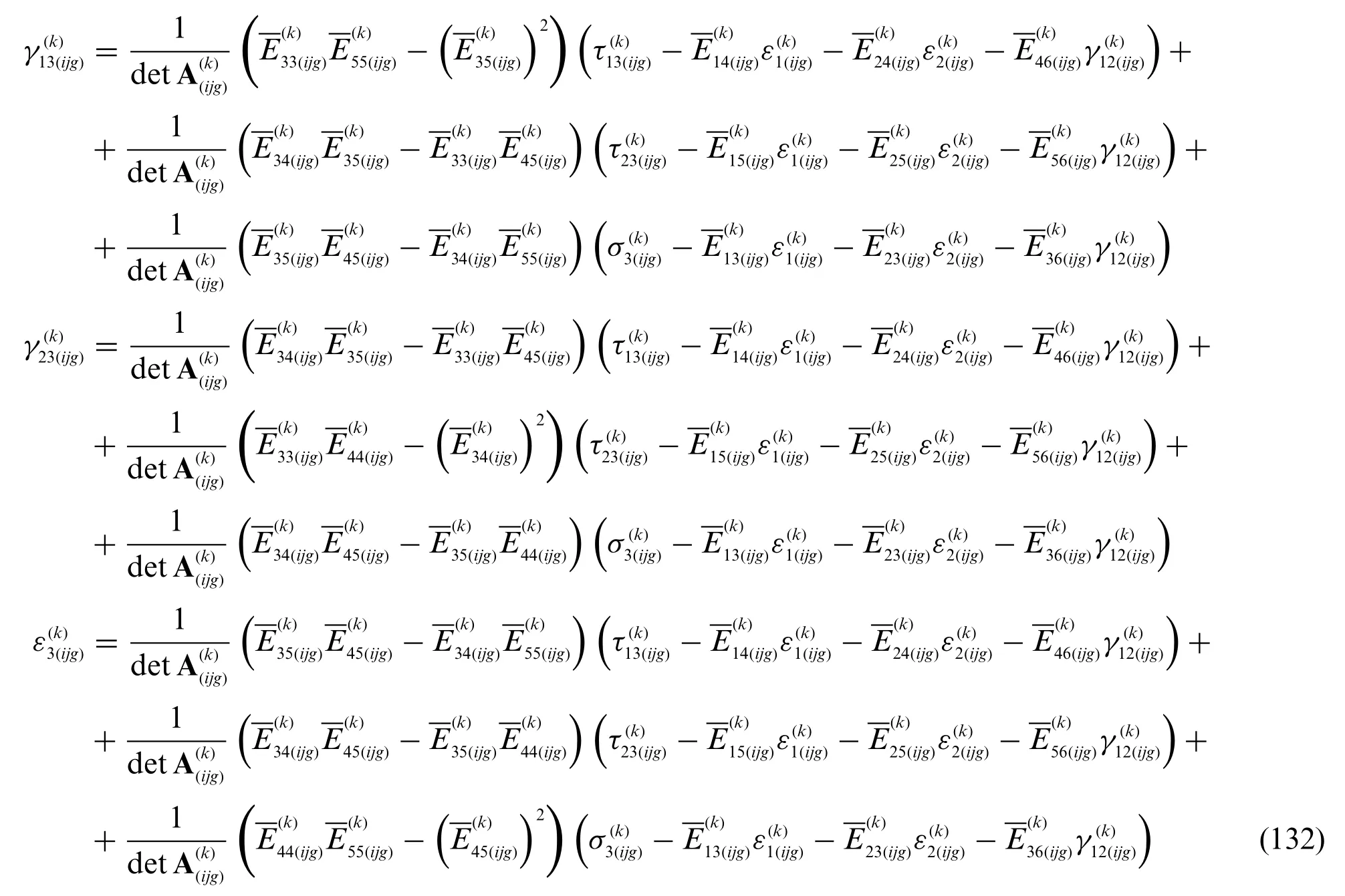
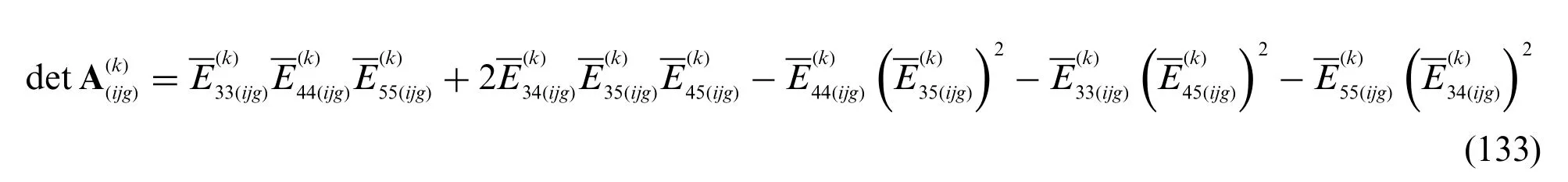
The complete procedure for the derivation of the recoveredstrain profiles is explained in reference[21].

9 Applications and Results

In the present section the LW formulation presented in the manuscript is applied to some structures of different curvature and materials,subjected to various load cases.In particular,the advantages of the present formulation compared with other trustworthy models are outlined.At a first stage,a fully-clamped beam subjected to a central concentrated load is considered,and the governing parameters of the load distributions presented in Eqs.(58)–(70)are calibrated with respect to a closedform analytical solution.After that,the static deflection of some thick shells characterized by zero,single and double curvature are calculated under different kinds of loads and boundary conditions.Furthermore,different kinds of lamination schemes have been considered,accounting for various numbers of laminae with both softcore and hardcore behaviours.In this way,the inconsistency of higher order ESL theories is outlined when such structures are employed,whereas the proposed higher order LW formulation provides very good performances with respect to three-dimensional refined solutions.

9.1 Validation for Concentrated Load Distributions

Let us consider a beam of lengthLx=10 m characterized by a rectangular cross section of dimensionsb=1 m andh=0.1 m made of isotropic AluminiumThe structure is clamped at its extremities,and it is subjected to a concentrated vertical load= -1000 N applied at its mid-span (Fig.3).A reference value for the maximum deflection of the structure has been calculated from the well-known Euler-Bernoulli Theory(EBT)according to the following expression:

beingI=bh3/12 the moment of inertia of the rectangular cross section.The same structure has been analysed with the GDQ method by means of Eq.(83) employing in Eq.(110) the FSDT kinematic field assumptions.In this way,the structure has been investigated based on the ESL two-dimensional approach.For each investigation,the percentage errore%of the solution with respect tohas been plotted,computed by means of the following expression:

As a matter of fact,in this case the boundary conditions are assigned so that a FCFC configuration is obtained according to Eqs.(86)and(87),following the nomenclature of Eq.(25).Thus,a parametric study has been performed so that the sensitivity of the main governing parameters of the concentrated load distributions presented in this manuscript is shown.

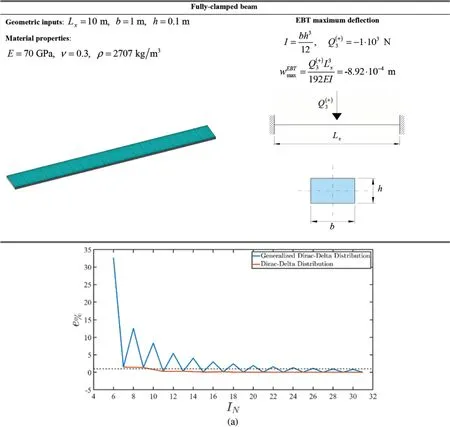
Figure 3: (Continued)

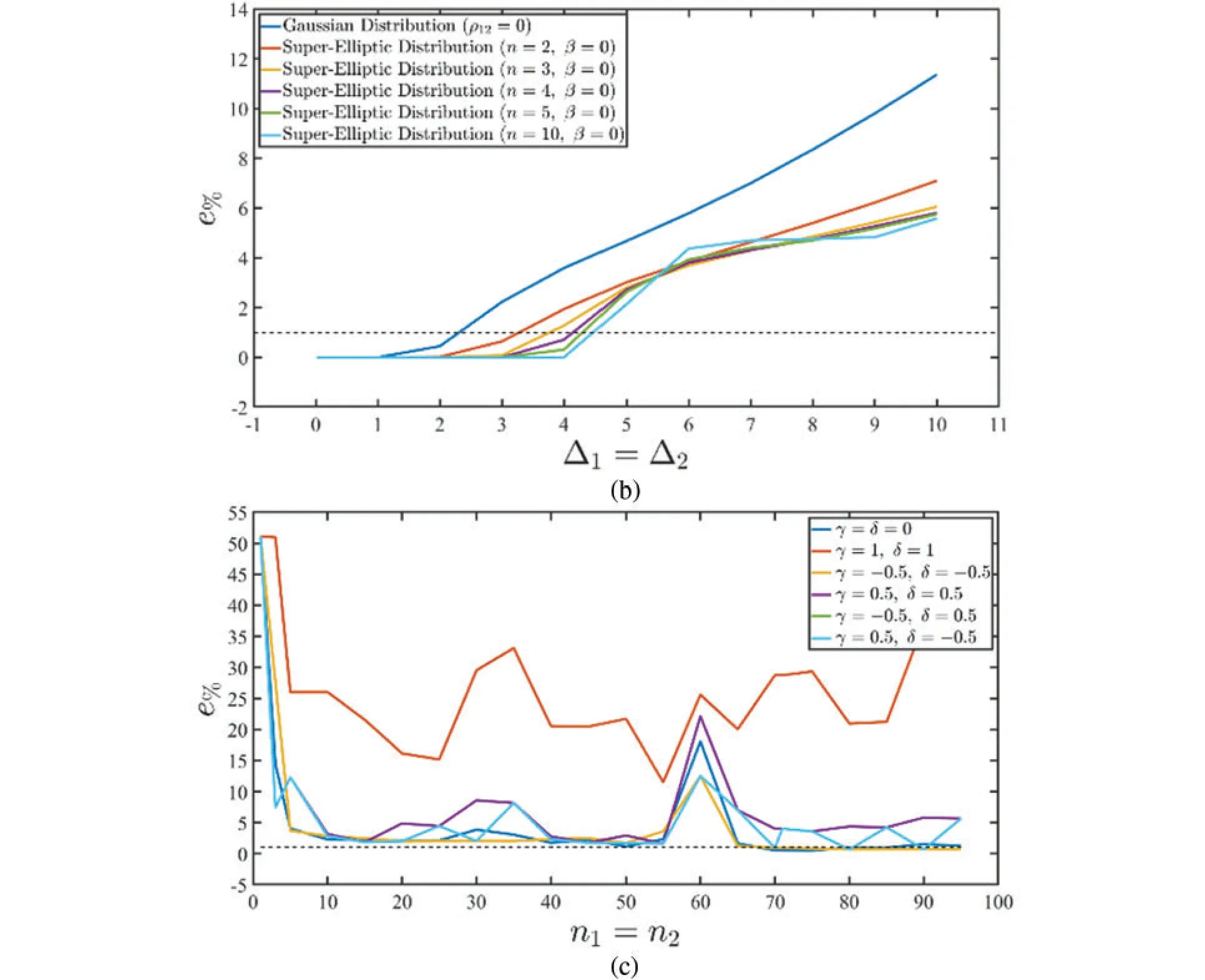
Figure 3: (Continued)

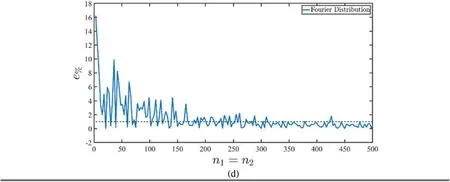
Figure 3:Calibration of the parameters of the distribution employed for the assessment of concentrated loads on the two-dimensional physical domain starting from a clamped beam subjected to a concentrated force at the middle span.A reference value of the maximum deflection has been calculated with the EBT closed-form solution.Accuracy of the numerical assessment of the Dirac-Delta function and the Generalized Dirac-Delta function (a).Accuracy of the results obtained when the Gaussian and the Super-Elliptic distribution are employed (b).Sensitivity analysis of a Jacobi polynomials-based modelling of the concentrated load (c).In (d),the precision of a two-dimensional model employing various numbers of Fourier series terms is outlined

In Fig.3a,the Dirac-Delta function of Eq.(68) has been adopted for the two-dimensional simulations according to the GDQ approach presented in Eq.(115).Moreover,the generalized version of the dispersion at issue has been studied employing the reduction to the computational nodes of the applied load according to the procedure of Eq.(116).SettingIM=31 for the numerical assessment of the two-dimensional model,the numberINof points along the beam length has been varied,showing that an increased grid dimension leads to more accurate results.More specifically,when a specific point of the computational grid is located in the middle span of the structure,i.e.,an even numberINis adopted,a percentage error(135)lower than 1%is obtained with a very reduced number of points.On the other hand,when a higher order interpolation procedure is required,at leastIN=24 discrete points are required to obtain stable and accurate results.This is due to the fact that the procedure based on a higher order interpolation of the Dirac-Delta function performs a reduction of the applied load to the adopted grid points,therefore a small accuracy loss is noticed.On the other hand,the GDQ-based integral-differential procedure for the numerical implementation of the Dirac-Delta function do not require any interpolation since the load is applied directly at the grid points.

In Figs.3b–3d,the sensitivity of the continuous distribution parameters is checked,settingIN=IM= 31.In particular,it has been shown that the Gaussian distribution of Eq.(59) provides a very good agreement with analytical solutions if the variance parametersare set equal to 2%.In the case of Super-Elliptic distributions(60)of various power exponents(Fig.3b),an increase ofn(k)does not lead to an improvement of precision of the simulation.In any case,stable results are reached if== 3%.This means that concentrated loads can be effectively described without any loss of accuracy if an equivalent pressure is applied to an area with a radius smaller than 3%of one edge of the physical domain.The efficiency of the formulation for concentrated loads by means of the Jacobi polynomials of Eq.(63)is shown in Fig.3c,where the percentage error of Eq.(135)is shown for differentγ(k)andδ(k)so that various polynomials belonging to the class at issue are employed.A sensitivity analysis with respect ton(k)1=n(k)2is shown in Fig.3c.In particular,it is shown that forγ(k)=δ(k)= -0.5 stable results with negligible errors are reached forn(k)1=n(k)2= 70,whereas other polynomials require higher order polynomials.Whenγ(k)=δ(k)=1,the proposed formulation is not capable of providing good results in any case.When the concentrated loads are implemented by means of a Fourier series expansion according to Eq.(61),at least 300 terms are required in the truncated series,as it has been shown in Fig.3d,telling that the singularity can be properly modelled with the superimposition of at least 300 sinusoidal functions.

Once the distribution of the main governing parameters are checked in Fig.3,the percentage error of Eq.(135) has been computed with respect to the discretization of the physical domain for all the continuous distributions presented in this manuscript(Fig.4).As it has been shown in the previous simulations,the employment of the Dirac-Delta function in its discrete form for the assessment of concentrated loads provides an excellent agreement with closed-form solutions even though a significative reduced number of DOFs are employed in the model.Among continuous functions,if the Super-Elliptic distribution of Eq.(60) is adopted,a fast stabilization of results with an excellent level of accuracy is seen regardless the selection of the distribution governing parameter.For this case,a constant valueδ= 0.02 has been selected,whereas the order of the distribution has been varied fromn(k)= 2 ton(k)= 10.In a similar way,the Gaussian distribution of Eq.(59),corrected according to Eq.(70),provides very good results even withIN= 11 grid points.The employment of the Fourier function of Eq.(61)withn(k)=315 terms rapidly leads to reduced values ofe%even though an oscillation is seen by varying the dimensionINof the discrete computational grid.Furthermore,for a Jacobi distribution,high values ofINare required to obtain a stable behaviour.The sensitivity of the computational grid has been checked for two different Jacobi polynomials of ordern(k)=71,namely the Legendre polynomialsand the Chebyshev polynomials of I kind,characterized byγ(k)=δ(k)= -0.5.As can be seen,the best agreement with respect to the closed-form solution of Eq.(134)is achieved when the Legendre polynomials are employed.

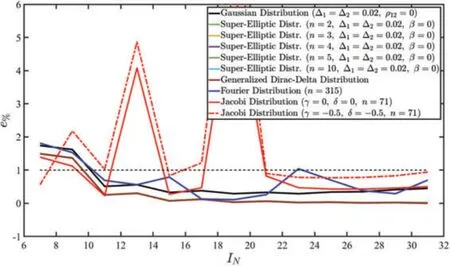
Figure 4: Parametric investigation of a clamped beam subjected to a concentrated load applied at the middle span of the structure.The discrepancy error has been calculated between the maximum deflection provided by the closed-form EBT and the numerical implementation proposed in the manuscript.The sensitivity of the computational grid has been outlined with respect to each load distribution

9.2 Validation of the LW Formulation

Once the governing parameters of the load distributions have been validated,the proposed LW methodology has been employed for the analysis of some structures of different features subjected to various loads and non-conventional boundary conditions.Accordingly,the examples of investigations have been selected so that the main advantages of the LW solutions are checked with respect to more simplified two-dimensional ESL methodologies.

In all simulations presented in this section,concentrated loads have been modelled by means of the Dirac-Delta function in Eq.(68),according to the numerical GDQ procedure.Furthermore,the three-dimensional static response of the structures at issue has been calculated from refined threedimensional simulations employing a classical 3D FEM.In this way,a reference solution is provided for validation purposes of the proposed methodology.The results have been provided in terms of the through-the-thickness dispersion of the three-dimensional kinematic and mechanical quantities in some points of the structure.

Different laminated structures have been considered,accounting for various stacking sequences with both hardcore and softcore behaviours.To this end,different classes of materials have been employed,i.e.,anisotropic,orthotropic and isotropic materials.For the first class we consider a Triclinic material[95],whose stiffness matrix is defined with respect to the material symmetry planes according to conventions Eq.(43):

For the sake of completeness,the density of the material has been taken equal toρ(k)= 7750 kg/m3.In order to provide a generally anisotropic material with softcore features,the so-called Triclinic-Soft material has been derived from Eq.(136),setting each stiffness constants equal to 1/1000 of the original one.

Referring to the group of orthotropic materials,the material stiffness properties have been expressed employing the well-known engineering constants,namely the three elastic modulithe shear moduliand the Poisson coefficientsThe relationship between the quantities at issue and the three-dimensional stiffness constantsfori,j=1,...,6 can be found in reference [21].In the following,the material properties of an orthotopic Carbon Fibre Reinforced Polymer(CFRP)of densityρ(k)=1824 kg/m3have been collected[95]:

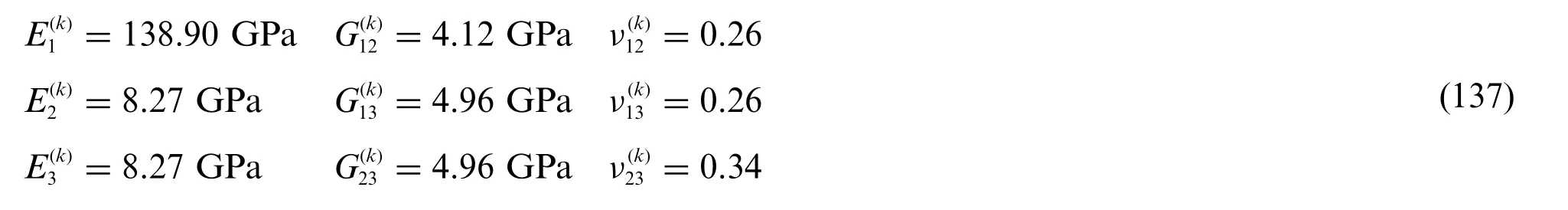
The orthotropic Graphite-Carbon Epoxyreads as follows:

In addition,the following lattice material named 3D Augmented Re-entrant Cellular Structure(3D ARCS),with densityρ(k)=66.468 kg/m3,has been considered:

Among the isotropic materials,a foam of densityρ(k)= 320 kg/m3has been considered characterized by an elastic modulusE(k)=0.232 GPa and a Poisson’s coefficientν(k)=0.2.Moreover,the Aluminium-Soft elastic modulus isE(k)= 70 MPa,whereas the Poisson’s coefficient isν(k)= 0.3 and the density has been set equal toρ(k)=2707 kg/m3.

The first example consists of a squared plate of dimensionsLx=Ly= 1 m composed by five laminates of equal thicknesshk= 0.02 m fork= 1,...,5 made of Triclinic material (first,third and fifth lamina) and Triclinic-Soft material (second and fourth lamina) of general orientations,namely(30/45/65/90).A concentrated load of reference valueQ(5+)= -1500 N and orientationsφ(5+)1=φ(5+)2=π/2 andφ(5+)3= 0 is applied at the top surface of the structure at the point locatedThe external constraints have been defined so that the West edge is fully-clamped,whereas the East one is constrained only for a half,setting a three-dimensional linear springs dispersion characterized byN/m3with=1 and an in-plane Super-Elliptic distribution withaccording to what exerted in Eq.(95).The static response of the structure has been calculated by means of the well-known FSDT and TSDT theories following the ESL approach of Eq.(110),together with the EDZ4 theory.Moreover,the employment of the Murakami’s zigzag function [21] has been checked too.Then,the analysis has been performed with the present LW formulation,accounting for various kinematic expansion orders employing Legendre polynomials.The choice of such interpolating function is based on the main outcomes of reference[24],where the sensitivity of the interpolating polynomials has been investigated with respect to the free vibration analysis.For an effective identification of the assumed thickness function,the nomenclature LD-Nis adopted,where“L”tells identify the LW approach,“D”refers to the fact that the present formulation is displacement-based,whereas “N”denotes the maximum expansion order within Eq.(26).

In Figs.5–7,the through-the thickness dispersions of the three-dimensional displacement field components,strains and stresses has been reported,respectively.These results refer to the point of the reference surface located atwithin the physical domain.Accordingly,the quantities at issue all refer to the previously discussed geometric reference systemO′α1α2ζ.Referring to Fig.5,it can be seen that the behaviour of the lamination scheme at issue cannot be well predicted by classical ESL approaches for both in-plane and out-of-plane coordinates.The EDZ4 theory provides a good agreement with the 3D FEM outcomes for the in-plane displacement field,but only the LD3 and LD4 are capable of best matching the previsions of the 3D FEM regarding vertical deflections.Similar considerations can be repeated for the strain components plotted in Fig.6.

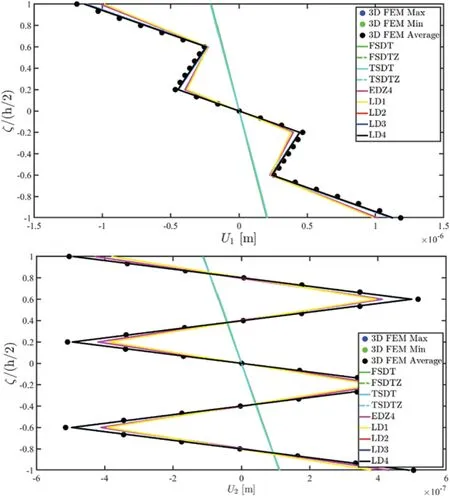
Figure 5: (Continued)

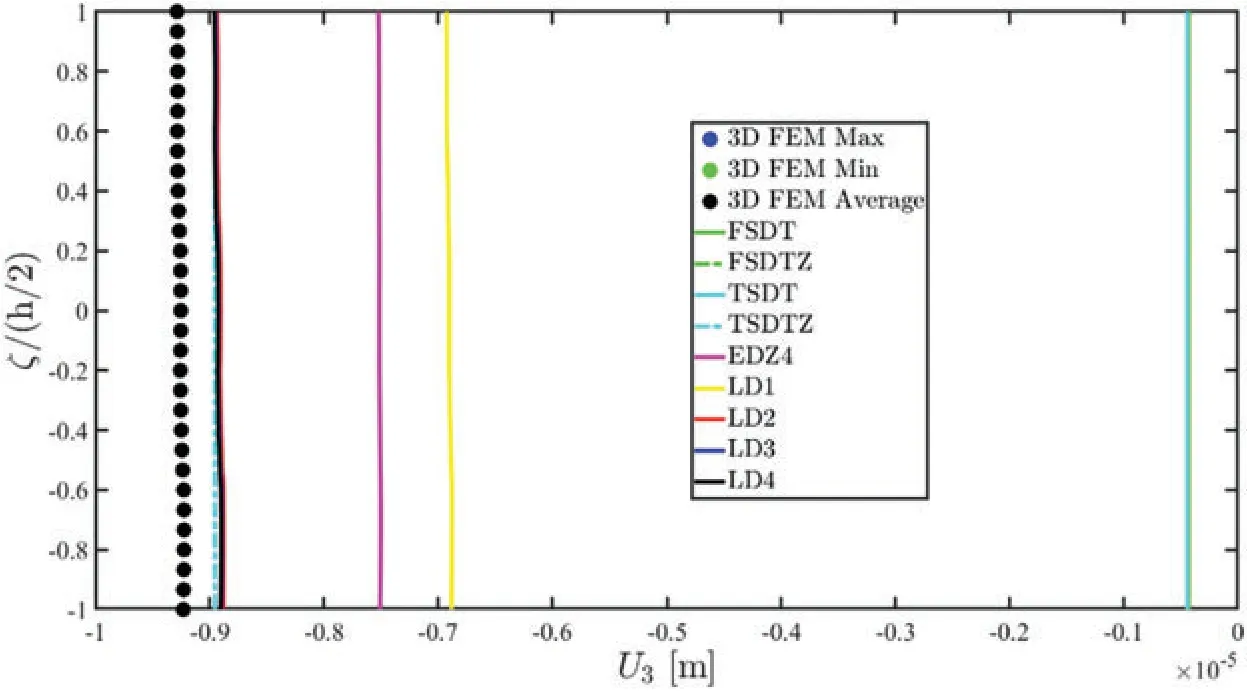
Figure 5:Through-the-thickness dispersion of the three-dimensional displacement field components Ui(α1,α2,ζ) for i = 1,2,3 of a laminated anisotropic rectangular plate subjected to a concen-trated load equal to = -1500 N and enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Figure 6: (Continued)

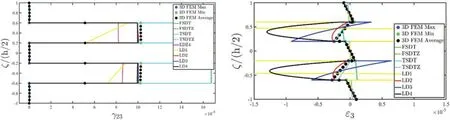
Figure 6: Through-the-thickness dispersion of the three-dimensional strain vector ε(α1,α2,ζ) of a laminated anisotropic rectangular plate subjected to a concentrated load equal to = -1500 N and enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Despite a higher order displacement field assumption(EDZ4)well predicts the in-plane axial and shear deformation unlike classical FSDT theory,a higher order LW theory is needed for the outof-plane distortions.The coupling effects and non-conventional behaviour of the selected stacking sequence is very clear in Fig.7,where the three-dimensional stress components are collected.As can be seen,all the simulation based on the LW model are capable,with a reduced number of DOFs,to predict the three-dimensional response of the structure provided by a huge computationally demanding formulation.In this way,very accurate results are provided for both in-plane and out-ofplane three-dimensional stress components starting from a two-dimensional formulation.It is also shown that higher order ESL theories with refined thickness functions does not lead good results,due to the complexity of the lamination scheme that can be found in the structure.Furthermore,the averaging method embedded in the 3D FEM for the extraction of theσ3out-of-plane normal pressure lead to a dispersion of results,whereas the proposed post-processing methodology provides a perfect fulfilment of the three-dimensional loading conditions.

Figure 7: (Continued)

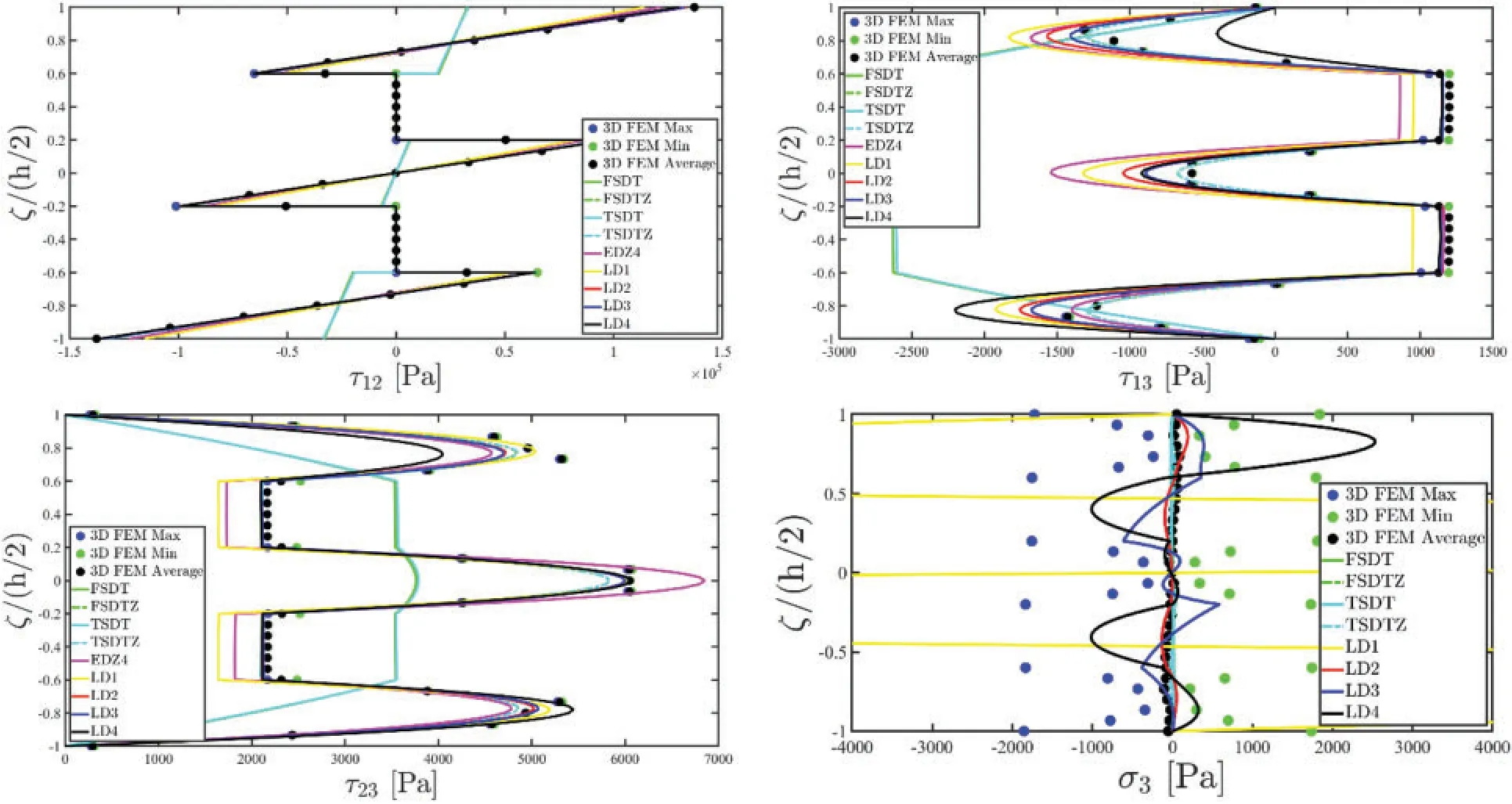
Figure 7: Through-the-thickness dispersion of the three-dimensional stress vector σ(α1,α2,ζ) of a laminated anisotropic rectangular plate subjected to a concentrated load equal to = -1500 N and enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Another simulation has been performed on an arbitrarily-shaped plate of five generally oriented layers composed by two external orthotropic sheets of Graphite-Carbon Epoxy material and a soft region characterized by two layers of Triclinic-Soft material and a central part made of isotropic foam.The distortion of the physical domain has been assessed by means of the blending functions presented in Eqs.(11)and(12),in which the boundary edges have been described by means of NURBS curves according to Eq.(13).The complete set of knots,weights and control points is reported in Fig.8.

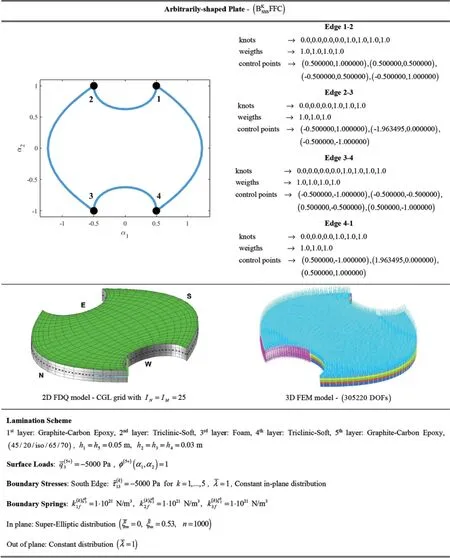
Figure 8: Geometric and mechanical properties of an arbitrarily-shaped plate composed by five anisotropic layers subjected to a surface load and a prescribed set of boundary stress.A threedimensional set of linear elastic springs has been adopted for the assessment of non-conventional external constraints

The structure is loaded from its top by a constant surface load and a distribution of stresses applied from one of its edges.The thickness distributions of the three-dimensional displacement field,strain and stress components have been depicted in Figs.9–11.

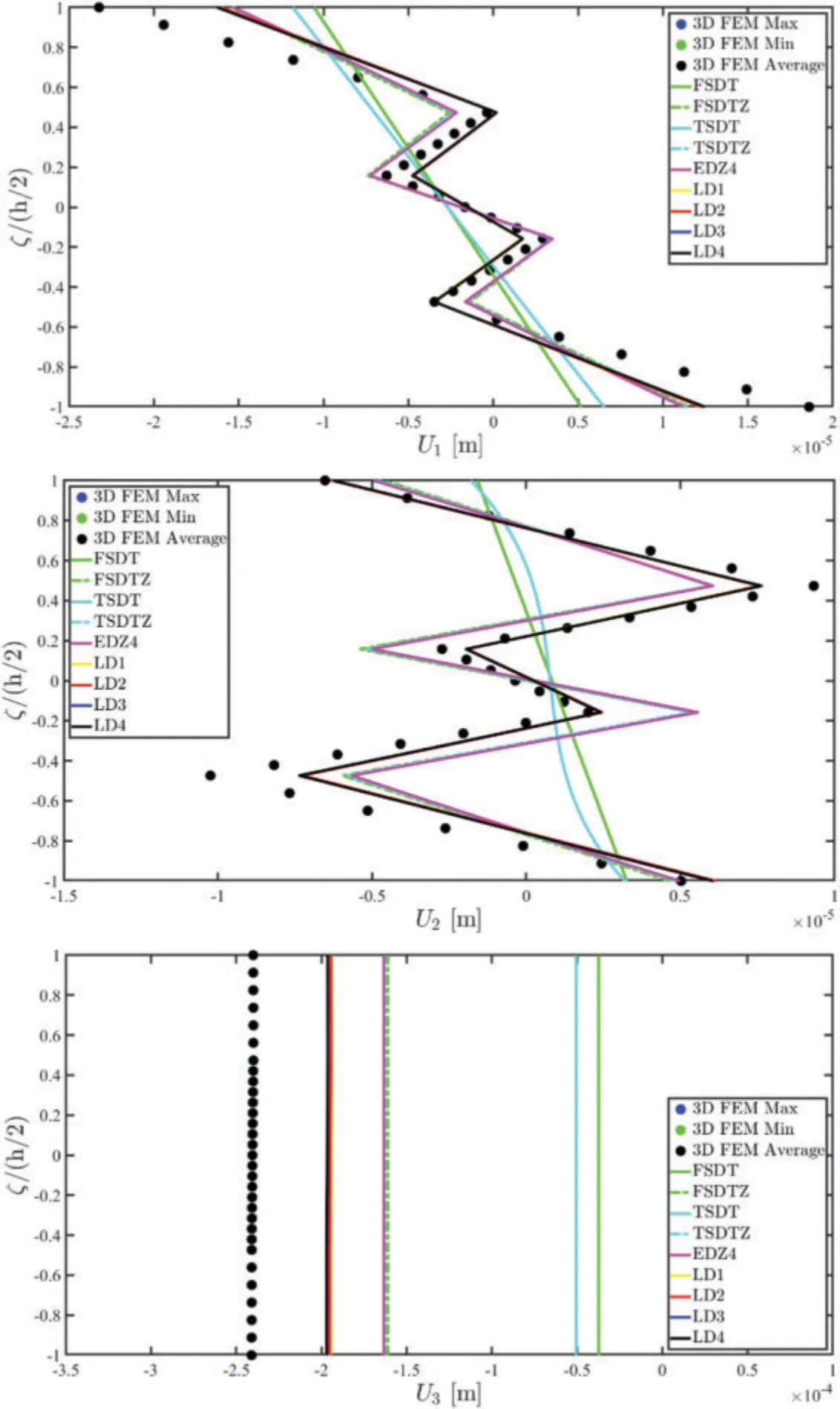
Figure 9:Through-the-thickness dispersion of the three-dimensional displacement field components Ui(α1,α2,ζ)for i = 1,2,3 of a laminated anisotropic rectangular plate of arbitrary shape subjected to a uniformly distributed load = -5000 Pa and a uniform distribution of boundary stress=-5000 Pa for k=1,...,5 applied at the South(S)side of the physical domain.The structure has been enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

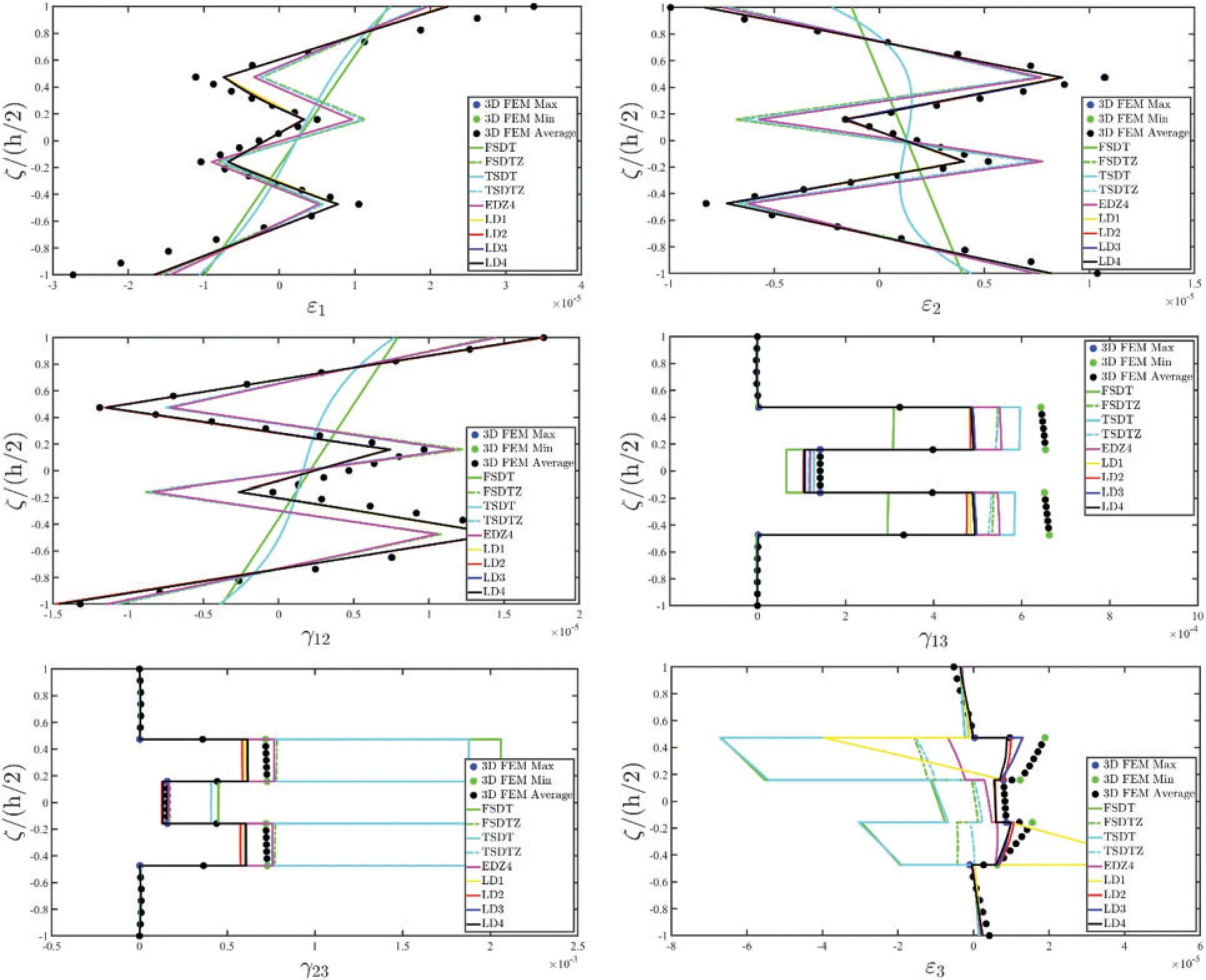
Figure 10: Through-the-thickness dispersion of the three-dimensional strain vector ε(α1,α2,ζ) of a laminated anisotropic rectangular plate of arbitrary shape subjected to a uniformly distributed load = -5000 Pa and a uniform distribution of boundary stress= -5000 Pa for k = 1,...,5 applied at the South (S) side of the physical domain.The structure has been enforced with nonconventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

As can be seen,the in-plane displacement components are characterized by a zigzag effect,whereas the out-of-plane one accounts for a constant through-the-thickness behaviour,as can be seen from Fig.9.Moreover,the LD4 two-dimensional approach best fits the previsions of the 3D FEM simulations in both in-plane and out-of-plane variables.If one refers to the strain components of Fig.10,is evident that the ESL approach is not capable of predicting the out-of-plane deformation and distortions of the central soft area of the laminated structure.In the same way,the three-dimensional stresses reported in Fig.11 provided by 3D FEM are well predicted for both in-plane and out-ofplane components if a higher order displacement field assumption is taken,due to the complexity of the lamination scheme,as well as the relative thickness of the structure.Furthermore,the results also show a perfect fulfilment of stress compatibility conditions at the interlaminar stage,even for the cases of adjacent layers of different stiffnesses.

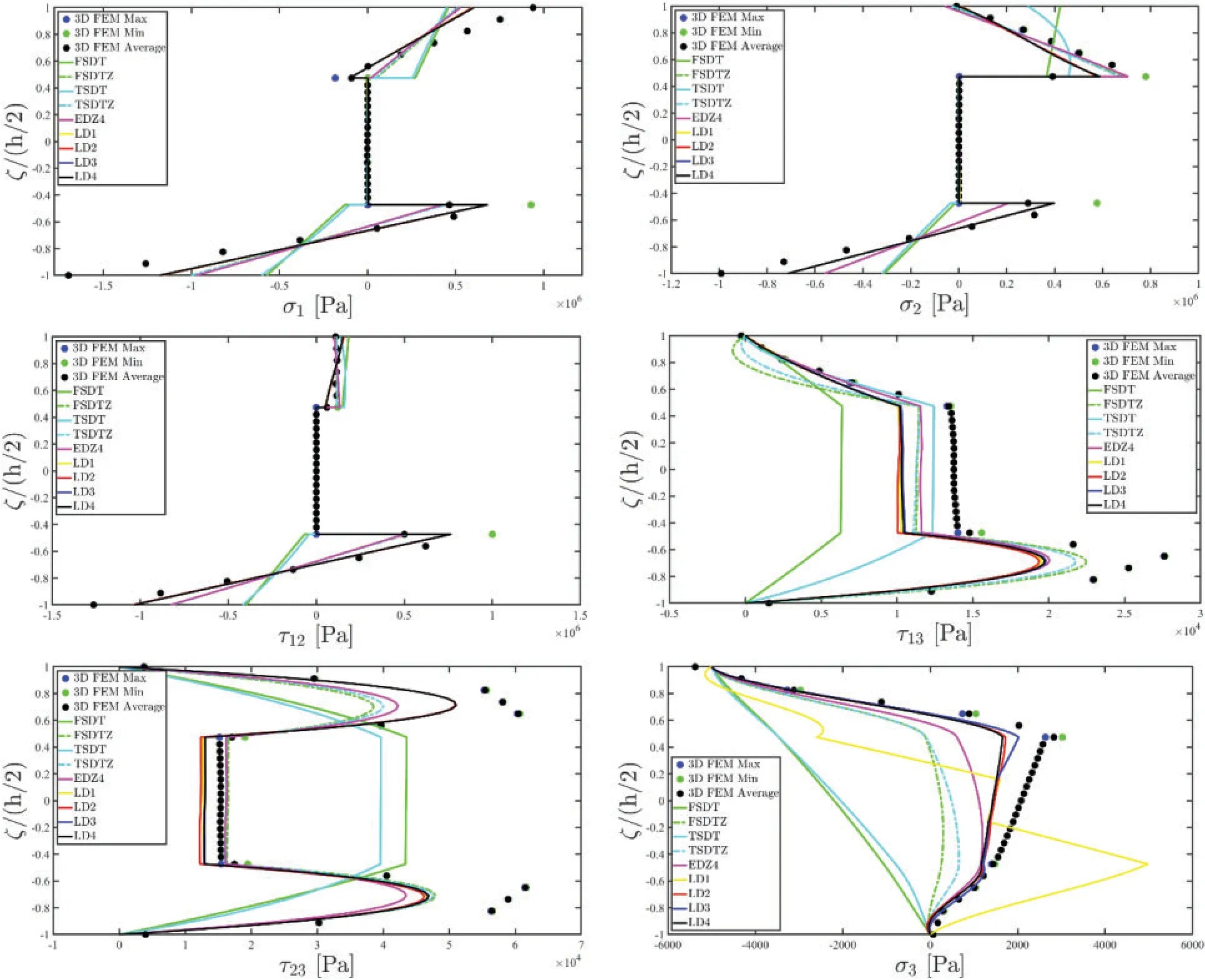
Figure 11: Through-the-thickness dispersion of the three-dimensional stress vector σ(α1,α2,ζ) of a laminated anisotropic rectangular plate of arbitrary shape subjected to a uniformly distributed load = -5000 Pa and a uniform distribution of boundary stress = -5000 Pa for k = 1,...,5 applied at the South (S) side of the physical domain.The structure has been enforced with nonconventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Two validation examples are now presented (Fig.12) in which the accuracy of the present LW theory has been checked also for the presence of the structural curvature.Accordingly,a singly-curved and a doubly-curved thick shell,namely a cylindrical and a spherical panel have been investigated.Referring to the cylindrical structure,the following parametrization of the global reference surface r(α1,α2)has been adopted[21]:

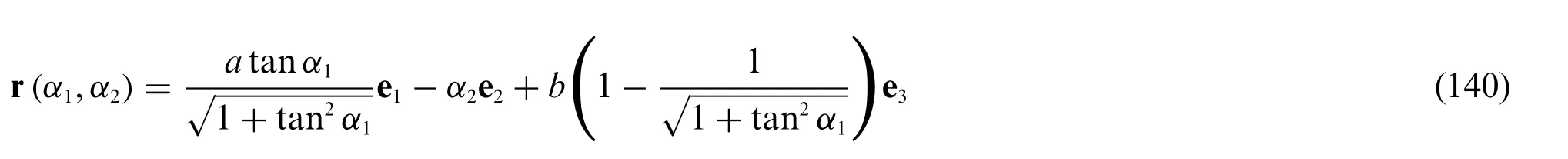
witha=b= 1 m.Thus,the physical domain has been described in principal coordinates so thatsettingα01=π/6,α11= 3α01,α02= 0 andα12= 1.The structure is made by three layers,with a lamination scheme defined according to the(45/0/30)orientation sequence.In particular,the two external layers of constant thicknessh1=h3= 0.03 m are made of a Triclinic material as presented in Eq.(136),whereas the central thick layer of thicknessh2=0.05 m is composed by Triclinic-Soft material.

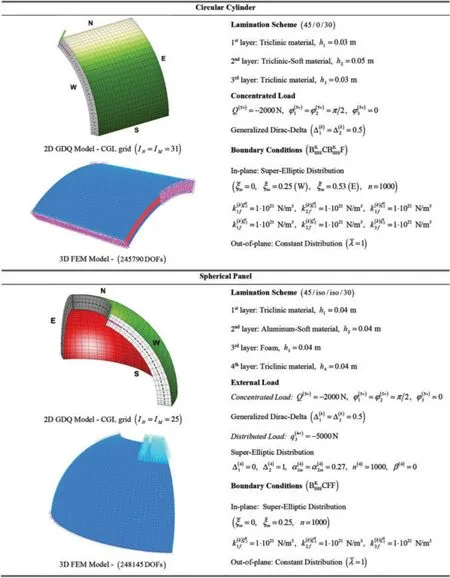
Figure 12:Geometric and mechanical main features of a singly-curved circular cylinder and a doublycurved spherical panel made of generally anisotropic materials of softcore and hardcore behaviour subjected to general loads and boundary conditions

A concentrated load with a reference value equal toQ(3+)= -2000 N has been applied at the central point of the physical domain,located atIts orientation with respect toα1,α2,ζhas been defined so that==π/2 and= 0.The external constraints,denoted withF employing a condensed notation,account for the adoption of the in-plane Super-Elliptic distribution of Eq.(95),settingn=1000 and the position parameters equal tofor the West edge,whereasis adopted in the East side of the structure.A CGL two-dimensional grid has been adopted,settingIN=IM= 31.The threedimensional response of the structure has been reported in Figs.13–15.It is evident that the predictions of the 3D FEM model regarding the displacement field can be matched only by LW approaches,among the two-dimensional formulations considered in this work(Fig.13).Moreover,an increased accuracy can be seen if the kinematic expansion order gets higher,especially for the out-of-plane displacement field components.Fig.14 shows the inconsistency of both classical and higher order ESL theories for the prediction of the three-dimensional strain components.Accordingly,the EDZ4 simulation does not fit the 3D FEM solution in the soft layer of the stacking sequence,whereas a perfectly matching can be seen when the LD4 theory is adopted for the out-of-plane elongation.Similar considerations can be made for the three-dimensional stress profiles,which have been all collected in Fig.15.Classical approaches like FSDT and TSDT do not provide good results with respect to the reference solution in any case,whereas for the in-plane stress components the higher order ESL theory can be adopted.However,for a correct prediction of the out-of-plane stress components in both hardcore and softcore layers the LW theory withN=4 is required.

Figure 13: (Continued)

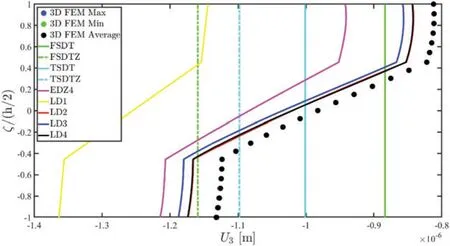
Figure 13:Through-the-thickness dispersion of the three-dimensional displacement field components Ui(α1,α2,ζ) for i = 1,2,3 of a laminated anisotropic circular cylinder subjected to a concentrated load equal to = -2000 N and enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of vari-ous orders.Thickness plots have been provided for the point of the reference surface located at

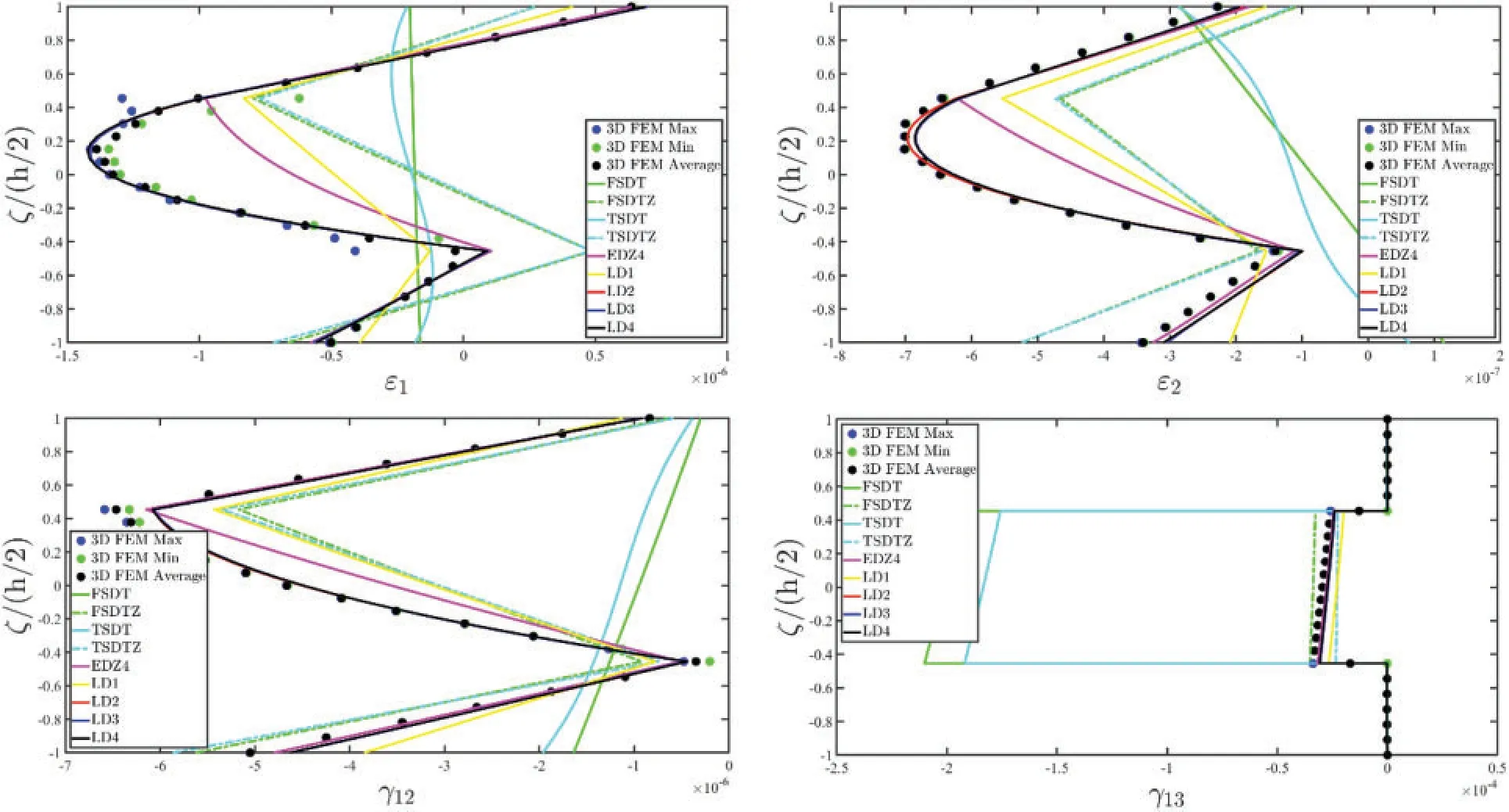
Figure 14: (Continued)

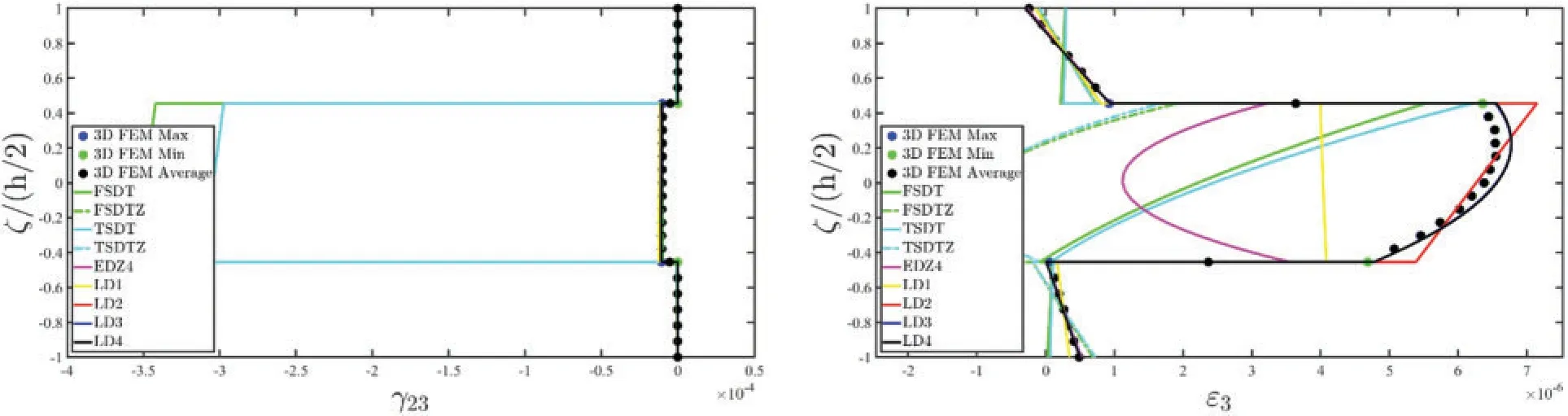
Figure 14: Through-the-thickness dispersion of the three-dimensional strain vector ε(α1,α2,ζ) of a laminated anisotropic circular cylinder subjected to a concentrated load equal to = -2000 N and enforced with non-conventional boundary conditions.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

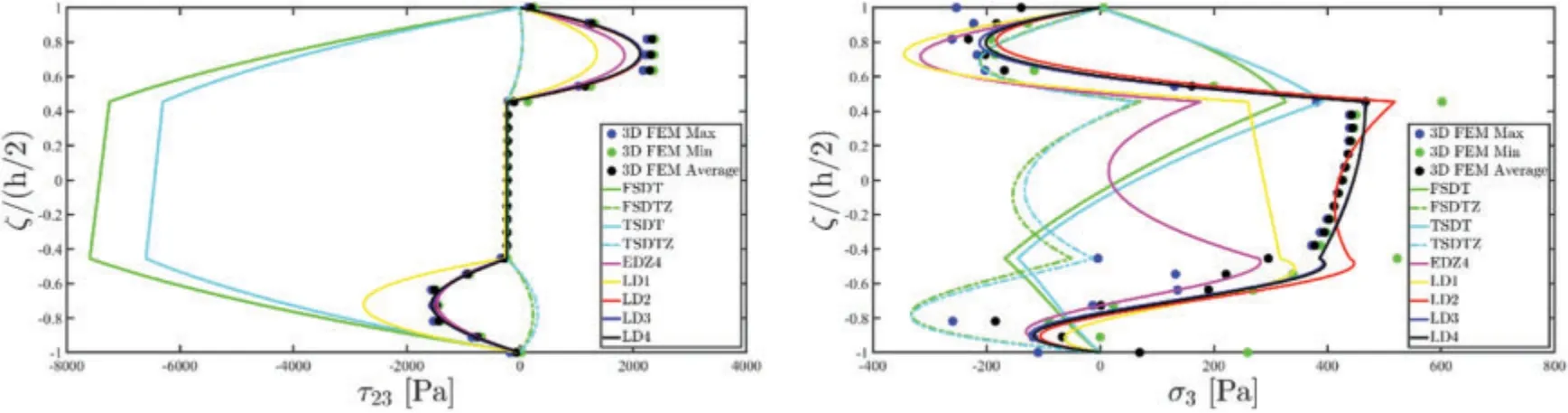
Figure 15: Through-the-thickness dispersion of the three-dimensional stress vector σ(α1,α2,ζ) of a laminated anisotropic circular cylinder subjected to a concentrated load equal to = -2000 N and enforced with non-conventional boundary conditions.The results have been provided employing

classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

The structural response of the spherical panel has been collected in Figs.16–18.Accordingly,the geometry of the structure (Fig.12) has been obtained from a parametrization of the shell reference surface r(α1,α2)obtained from the expression of a revolution surface characterized by a circular meridian[21],reading as:

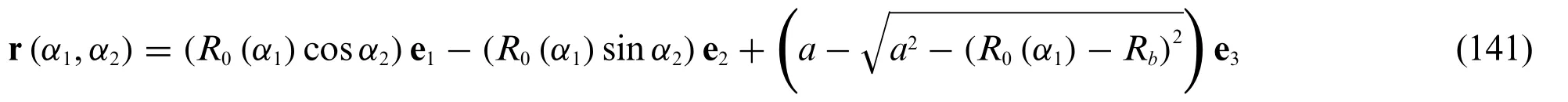
whereR0(α1)is defined for this example according to the following expression:

Figure 16:Through-the-thickness dispersion of the three-dimensional displacement field components Ui(α1,α2,ζ) for i = 1,2,3 of a laminated anisotropic spherical panel subjected to a concentrated load equal to = -2000 N and a surface pressure = -5000 Pa applied in a specified region of the physical domain.Non-conventional boundary conditions have been enforced to the structure.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Figure 17: Through-the-thickness dispersion of the three-dimensional strain vector ε(α1,α2,ζ) of a laminated anisotropic spherical panel subjected to a concentrated load equal to = -2000 N and a surface pressure = -5000 Pa applied in a specified region of the physical domain.Nonconventional boundary conditions have been enforced to the structure.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

The last simulation has been performed on a doubly-curved shell structure,namely a Super-Elliptic panel,a revolution surface whose parametrization has been reported in Fig.19.Five layers of different thicknesses have been superimposed,accounting for two hardcore external laminae of orthotropic and generally anisotropic syngonies.The softcore area has been obtained with an isotropic foam,a Triclinic-soft material and an orthotropic pantographic layer of 3D ARCS,whose homogenized engineering constants have been reported in Eq.(139).The structure is loaded with a concentrated load pressure applied at the centre of the structure,namely at the pointof the physical domain.A Super-Elliptic distribution of linear elastic springs is applied so that a portion of the East side of the structure is clamped.In Fig.19 the deflection of the structure along some meaningful parametric lines have been reported employing a CGL grid withIN=IM=25 point and a LD4 displacement field assumption.

The three-dimensional response of the structure has been obtained employing the equilibriumbased recovery procedure for the point located atand it has been collected in Figs.20–22.The employment of different kinematic expansion orders within the present LW formulation does not significantly affect the results in terms of displacement field components as it is evident from Fig.20,unlike classical and higher order ESL theories which are significantly affected by the selection of the field variable within the unified formulation.Similar considerations can be made for the three-dimensional strain components collected in Fig.21,where the LW results are in perfect agreement with each other,whereas the ESL approach is subjected to a certain instability in the results.In Fig.22,the results in terms of stress components have been provided,showing that the LW methodology provides an accurate description of the zigzag curve.In particular,referring to the out-of-plane shear components,the softcore region,characterized by three different parts,provides a change in the inclination that ESL theories are not capable of predicting at all.

Figure 20: (Continued)

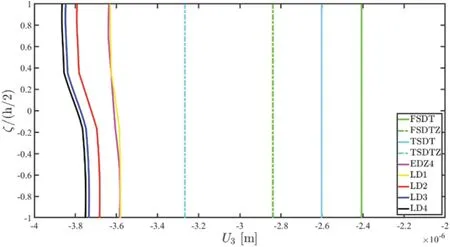
Figure 20:Through-the-thickness dispersion of the three-dimensional displacement field components Ui(α1,α2,ζ)for i=1,2,3 of a laminated anisotropic Super-Elliptic Panel subjected to a concentrated load equal to =-5000 N applied at the central point of the physical domain.Non-conventional boundary conditions have been enforced to the structure.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

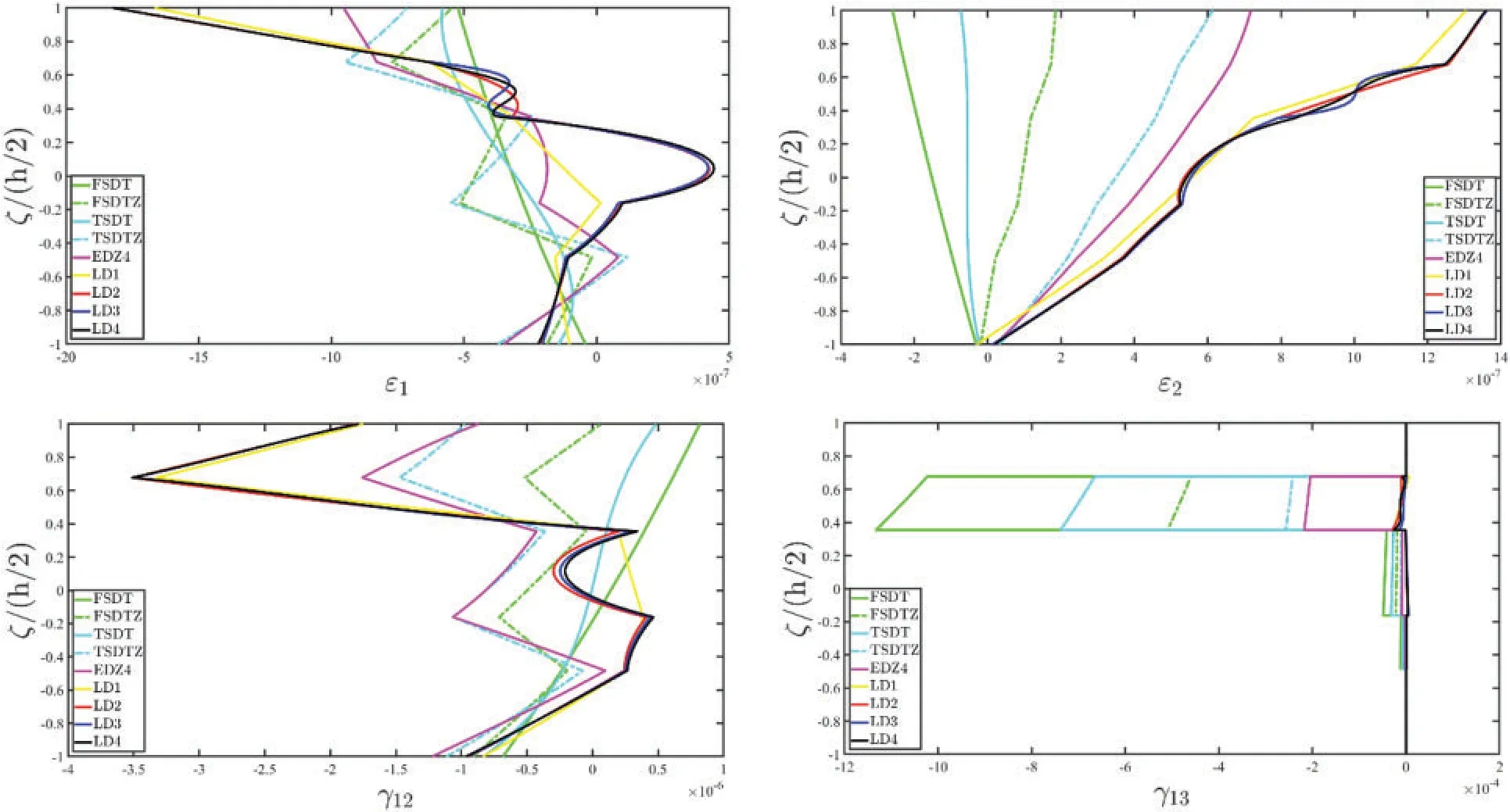
Figure 21: (Continued)

Figure 21: Through-the-thickness dispersion of the three-dimensional strain vector ε(α1,α2,ζ) of a laminated anisotropic Super-Elliptic Panel subjected to a concentrated load equal to =-5000 N applied at the central point of the physical domain.Non-conventional boundary conditions have been enforced to the structure.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

Figure 22: (Continued)

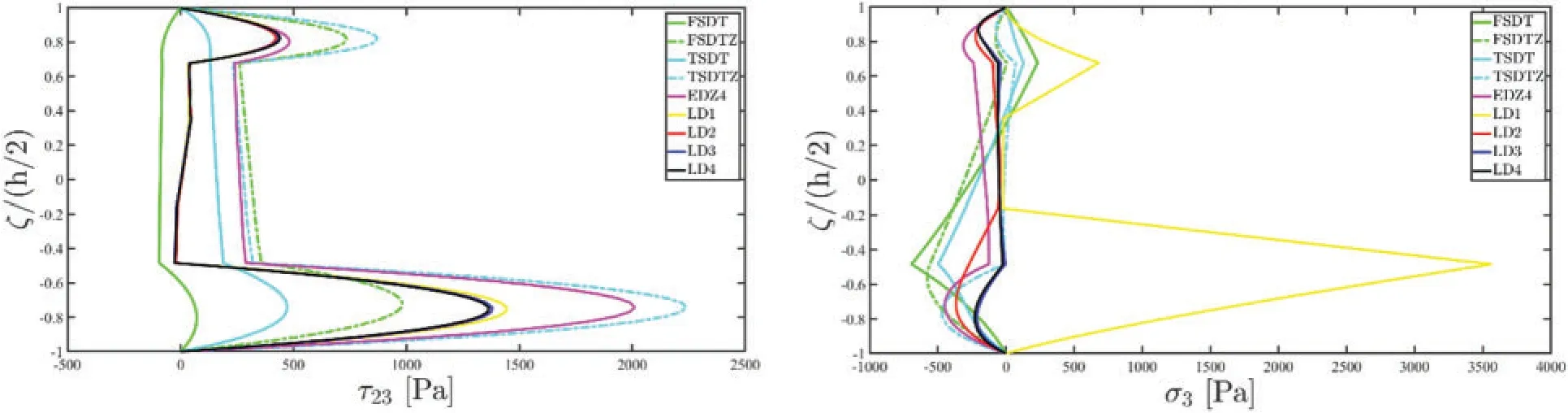
Figure 22: Through-the-thickness dispersion of the three-dimensional stress vector σ(α1,α2,ζ) of a laminated anisotropic Super-Elliptic Panel subjected to a concentrated load equal to =-5000 N applied at the central point of the physical domain.Non-conventional boundary conditions have been enforced to the structure.The results have been provided employing classical ESL theories and LW formulations of various orders.Thickness plots have been provided for the point of the reference surface located at

To sum up,it is clear that in the case of lamination scheme employing a meaningful number of superimposed laminae,the static deflection is characterized by a non-conventional behaviour due to a series of warping and coupling effects occurring between two adjacent laminae.For this reason,among two-dimensional theories,the LW implementation turns out to be a key for the determination of the three-dimensional response of the structure object of investigation.

10 Conclusions

In the present work,an innovative two-dimensional formulation has been proposed,based on the LW approach,for the linear static assessment of laminated doubly-curved shell structures made of generally anisotropic materials with arbitrary orientation.The displacement field variable has been described based on a unified formulation and higher order expansion employing different interpolating polynomials.An effective procedure has been provided for the assessment of general dispersions of surface loads applied at each layer of the laminated structure.Furthermore,the concentrated load has been successfully modelled with the Dirac-Delta function,accounting for the shell curvature effects.Moreover,a normalization of an arbitrary smooth function has been proposed,so that the singularities can be effectively simulated within the continuum model.The fundamental governing equations,derived by means of the Minimum Potential Energy Principle,have been tackled numerically in the strong form with the GDQ procedure.Then,the three-dimensional response of the structure has been recovered starting from the three-dimensional equilibrium equations.Some examples of investigations have been explored in the manuscript,in which the validity of the proposed LW approach has been validated with respect to refined three-dimensional trustworthy simulations based on the FEM,showing an excellent accuracy.Moreover,the present LW approach has allowed to properly catch a series of interlaminar coupling effects occurring in the lamination scheme,as well as several issues related to the presence of the curvature,employing a significantly reduced computational cost.

Appendix A.Generalized coefficients for the assessment of boundary conditions

We report the complete expression for coefficients of matrix O(kτη)αiαjemployed in Eq.(56),defined for eachk-th layer of the laminated structure,settingk= 1,...,landαi,αj=α1,α2.Accordingly,they relate the generalized stress resultants referred to theτ-th kinematic expansion order to the displacement field components of theη-th higher order assumptions,accounting for the anisotropic behaviour of each lamina and the shell curvature effects.

Appendix B.Higher order fundamental operator of the governing equations

Referring to a genericτ-th andη-th kinematic expansion order,the interested reader can find the complete expression of componentsfori,j= 1,2,3 of operator L(kτη)referred to thek-th layer of the stacking sequence,withk=1,...,l,occurring in the fundamental governing relations of Eq.(80),according to the notation introduced in Eq.(81).Accordingly,the coefficients at issue have been collected by row.

First row of the fundamental operator

Second row of the fundamental operator

Third row of the fundamental operator

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.