具有部分分数阶扩散项的三维Navier-Stokes 方程的适定性
黄耀芳,李 莉,董 玉,张洪林
(宁波大学 数学与统计学院,浙江 宁波 315211)
Navier-Stokes 方程描述了黏性流体的运动,而三维不可压方程解的适定性问题仍然是公开的难题.1934 年,Leray[1]证明了不可压Navier-Stokes 方程全局弱解的存在性.到目前为止,最优的正则性结果仍然归功于Caffarelli 等[2],他们证明了Navier-Stokes 方程的任何适当弱解的奇异集具有一维Hausdorff 零测度.后来,Lin[3]使用紧性方法证明了相同的结果.Vasseur[4]使用De Giorgi 为椭圆方程引入的方法证明了同样的结果.由于没有足够的耗散来控制方程的非线性性,因此标准的Navier-Stokes 方程是超临界的.
为了增强Navier-Stokes 方程的耗散,诸多学者进行了一系列改进.考虑具有超耗散的广义Navier-Stokes 方程
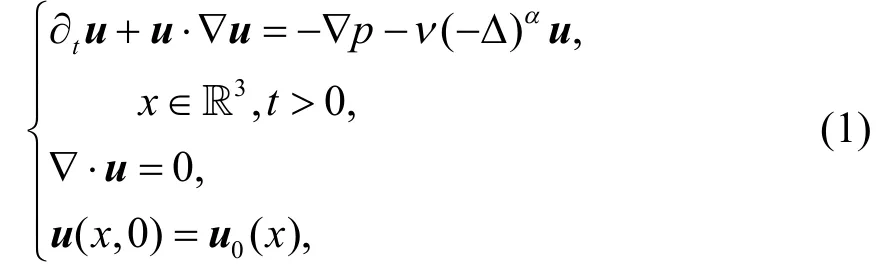
其中u=(u1,u2,u3)表示流体的速度场,p代表压力.如果α≥ 5/4且初始数据是光滑的,则该方程具有全局光滑解并且解是具有唯一性的[5-8].2009年,Tao[9]研究了具有以下对数形式的超临界超耗散项的Navier-Stokes 方程:
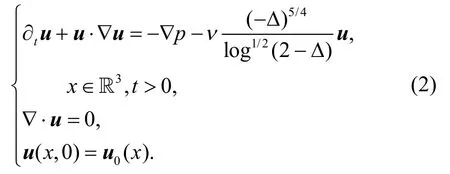
Tao 改进了上述结果并发现方程(2)对任何光滑且有紧支集的初始数据都有全局光滑解.Barbato 等[10]通过在对数弱耗散项上引入较弱的条件,进一步改进了Tao 的研究结果.学者们还研究了具有超耗散的不可压磁流体动力学方程,但结果并不完全一样[7,11].
一些数学家通过研究具有部分超耗散的Navier-Stokes 方程来改进方程(1)的结果.Yang 等[12]减少了方程(1)中的超耗散,研究了以下具有部分耗散的三维Navier-Stokes 方程的全局正则性:
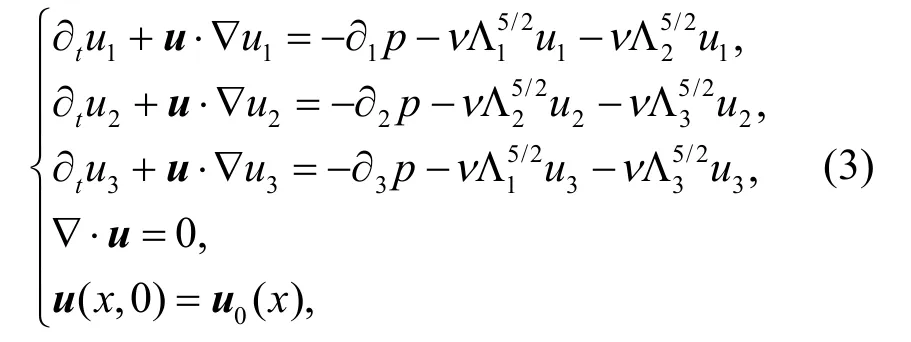
并证明了当u0∈H1(R3)时,方程(3)的强解具有全局存在性和唯一性.2021 年,Li 等[13]证明了u0∈Hs(R3)(s> 5/2)时方程(3)H s解的全局存在性和唯一性.
当所有方程中都去除沿x3方向的超耗散时,可得

受Yang 等[12]研究的启发,本文从u2和u3的方程中去除沿x3方向的超耗散,考虑以下不可压Navier-Stokes 方程的适定性:
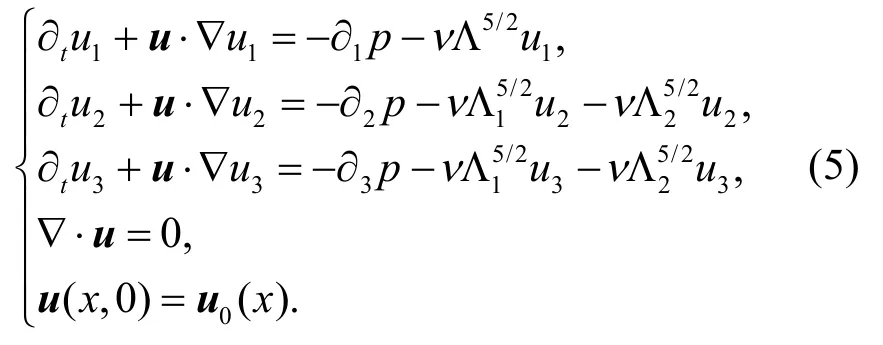
本文证明了方程(5)的1H解的全局存在性和唯一性.需要注意的是,如果u1,u2没有沿x3方向的耗散,即将从u1,u2的方程中去掉,则使用此方法不能证明以下问题的适定性:
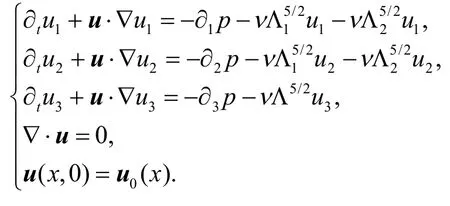
1 主要结果
首先介绍一些符号.在本文其余部分,分数阶拉普拉斯算子(-Δ)α是通过傅里叶变换定义的[14]:

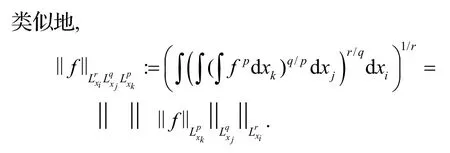
本文的主要结果可表示为如下两个定理.
定理1 假设u0∈H1(R3),则方程(5)存在一个全局解u,且满足
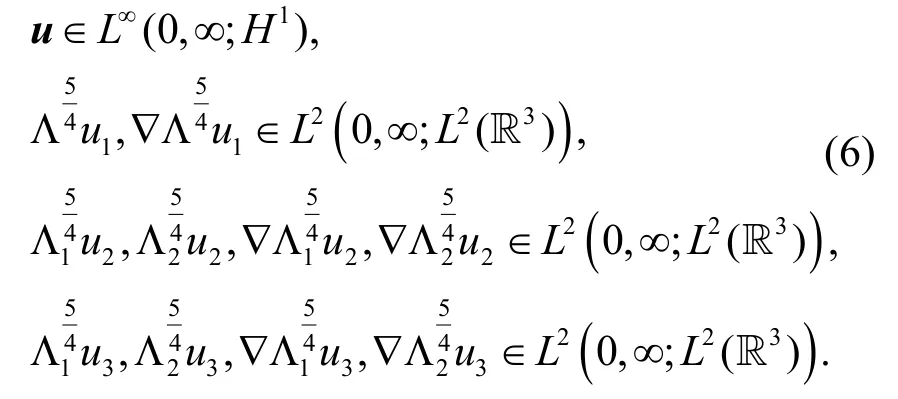
此外,如果有一个解在更好的函数空间,则可以得到下面的唯一性结果.
定理2 如果u(1),u(2)是方程(5)的两个解,它们都满足式(6)并且∇9/4u(2)∈L2(0,∞;L2(R3)),则u(1)≡u(2).
2 全局存在性和正则性的证明
首先给出用于证明上述定理的预备知识.
引理1 (Sobolev 嵌入不等式)假设2 ≤p≤∞且s>d(1/2 -1/p),则存在一个仅依赖于d,p和s的常数C,使得

此外,如果2 ≤p<+∞,式(7)对s=d(1/2 -1/p)也成立.
为了交换两个Lebesgue 范数,证明中将会使用下列Minkowski 不等式和Gagliardo-Nirenberg 不等式.
引理2 (Minkowski 不等式)假设f(x,y)是一个测度函数,x∈Rm且y∈Rn,如果1 ≤q≤p≤∞,则


下面证明解的全局存在性和正则性.取方程(5)与u的内积,分部积分并利用∇·u=0得
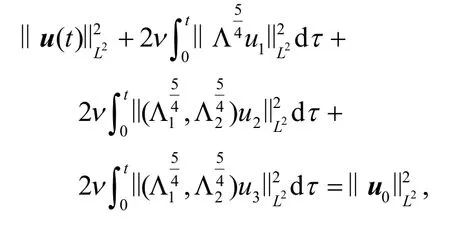
其中使用了如下记号:
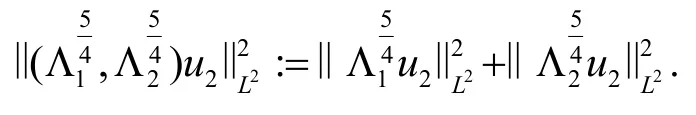
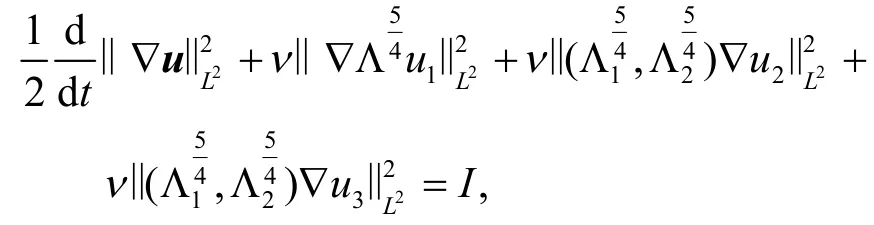
其中
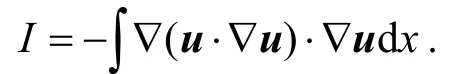
在利用散度条件∇·u=0后,可以将I写为

由于对u1及其导数有更多的控制,所以在此只给出I2和I3估计的计算.首先考虑I2,
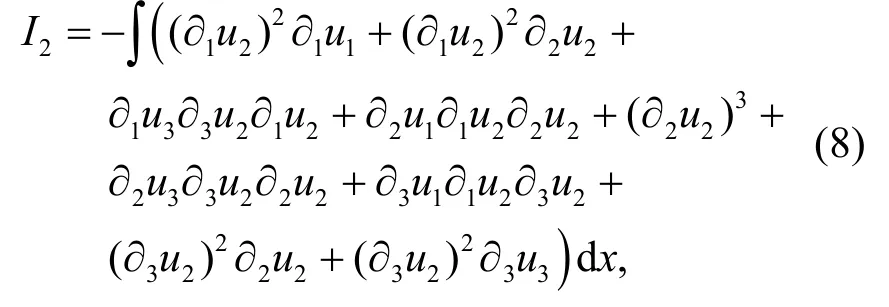
将方程(8)中的项根据它们出现的顺序依次标记为I21,I22,…,I29.
针对I21,通过分部积分有
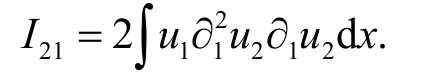
利用Hölder 不等式和引理2 得
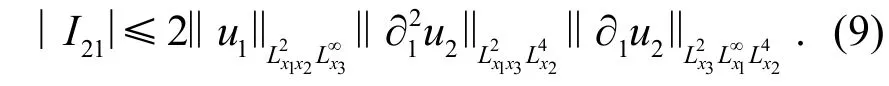
由Sobolev 不等式可得

和
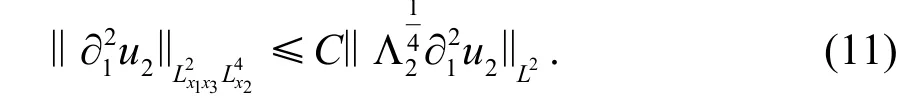
由基本不等式
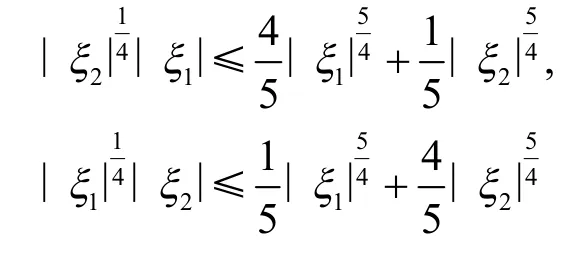
和Plancherel 定理,有
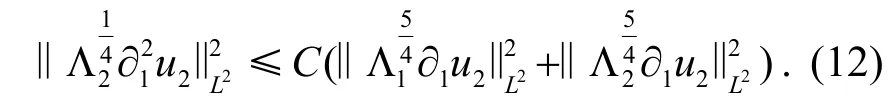
应用引理1 和引理3,取p=∞和s=1,有

其中使用了插值不等式
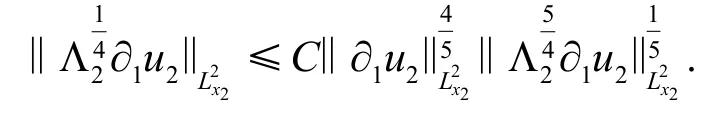
综合估计式(9)~(13)并使用Young 不等式,有
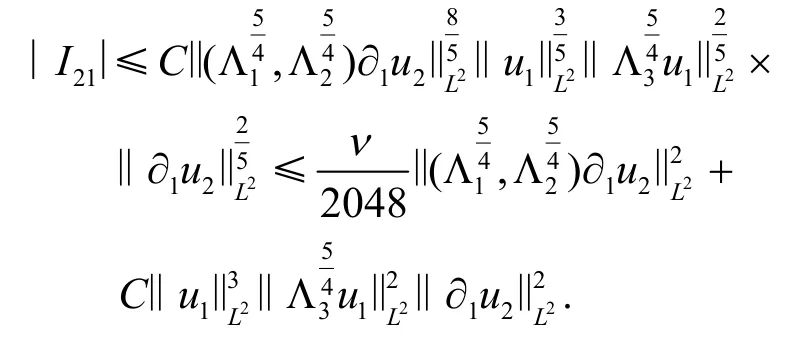
对于I22的估计,可以利用类似于I21估计的方法.通过分部积分法有
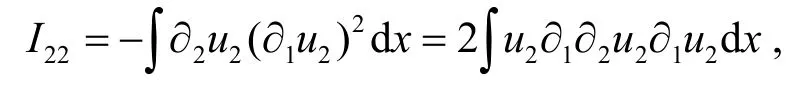
事实上,
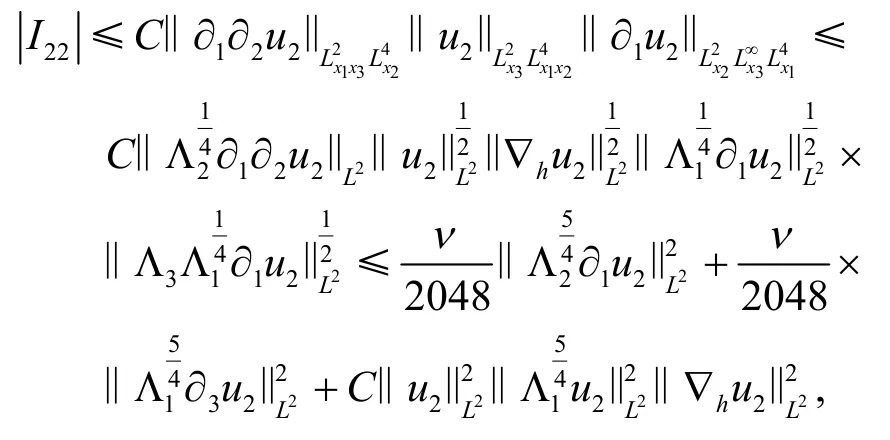
其中 ∇h=(∂1,∂2).
针对I23估计,通过分部积分有
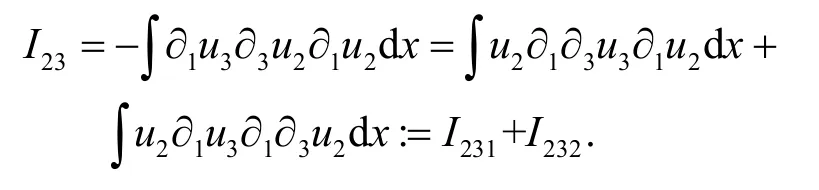
事实上,
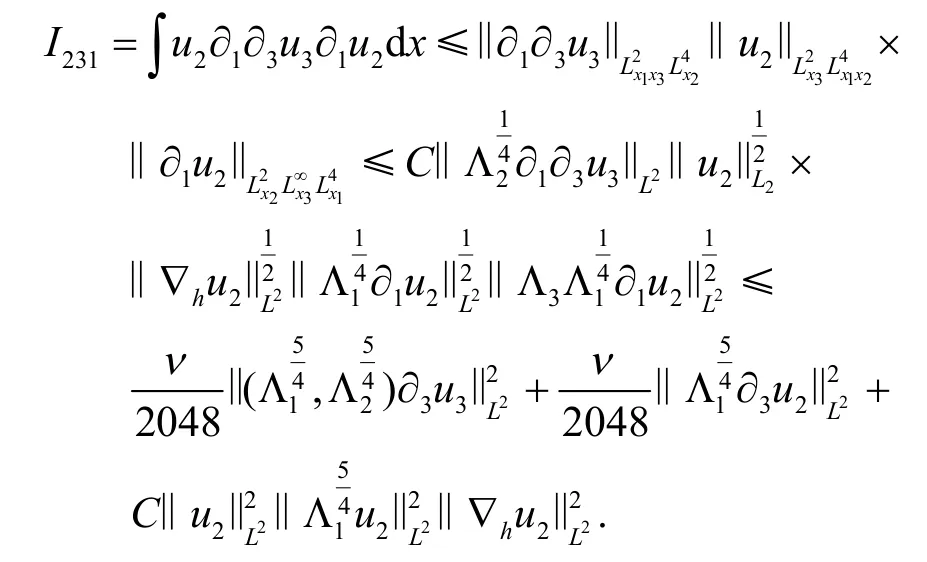
类似地,
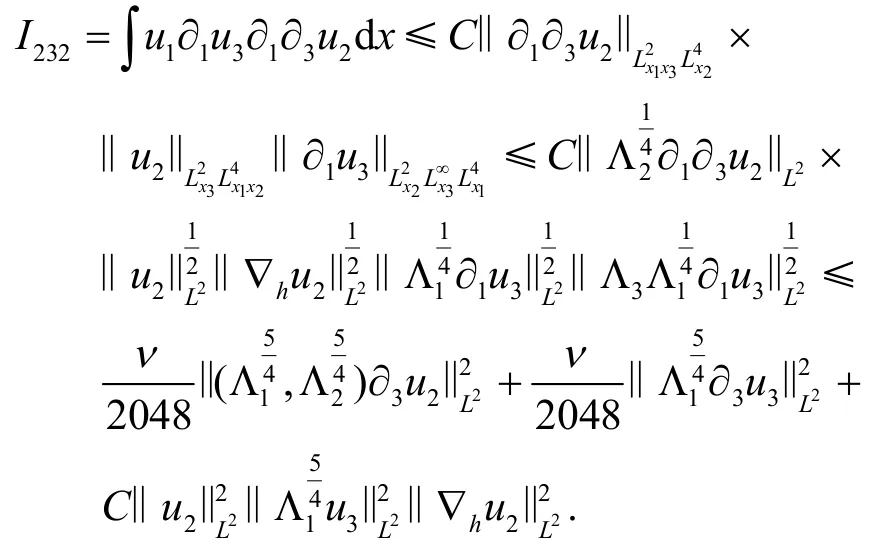
这就确定了I23的估计.
对于I24的估计,通过分部积分有
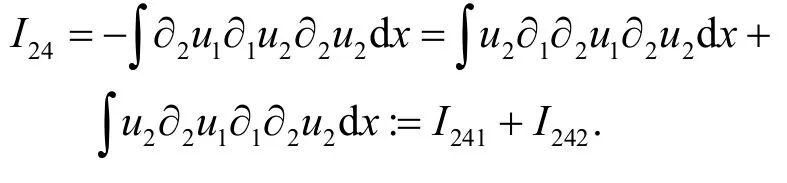
事实上,

类似地,
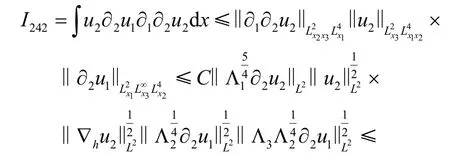
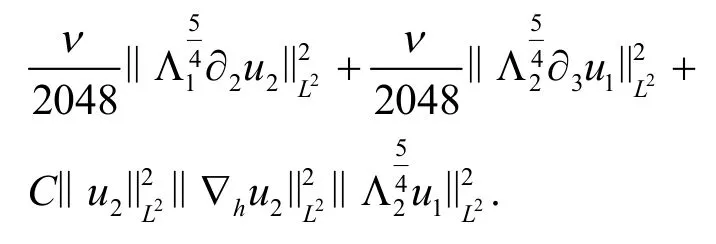
这就完成了I24的估计.
为了估计I25,利用分部积分得到
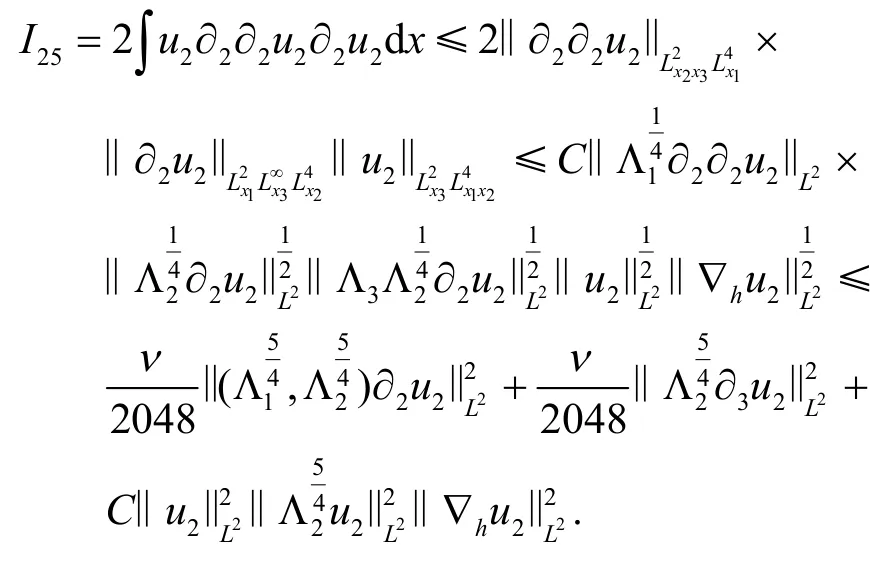
对I26的估计与I24类似.通过分部积分有

事实上,
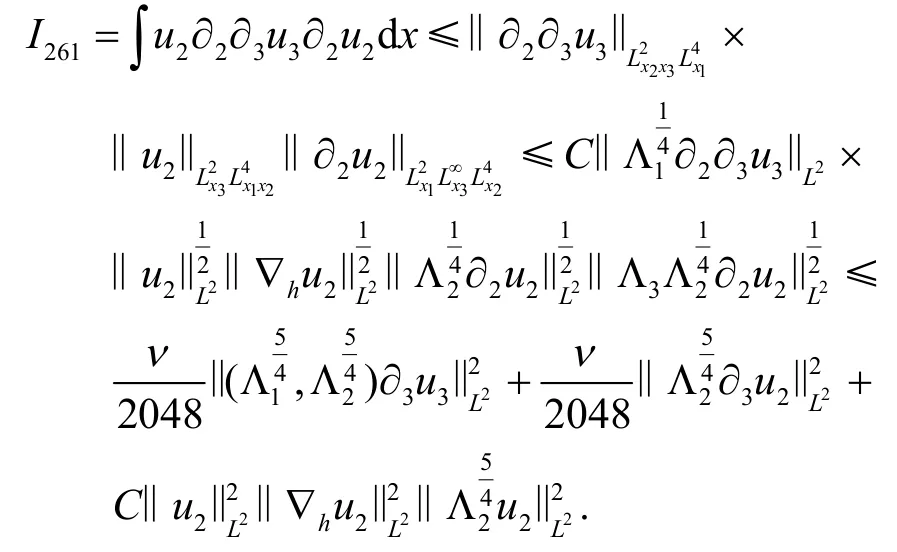
同理得
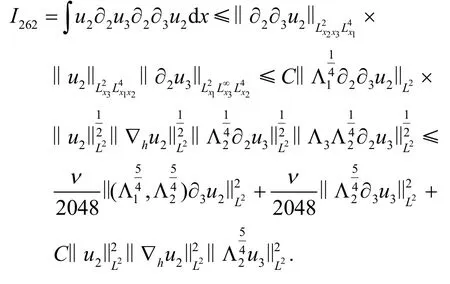
因此就得到了I26的估计.
为估计I27,通过分部积分可以得到
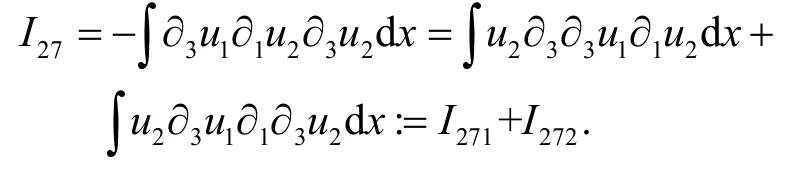
对I271的估计与I22的估计类似,因此有
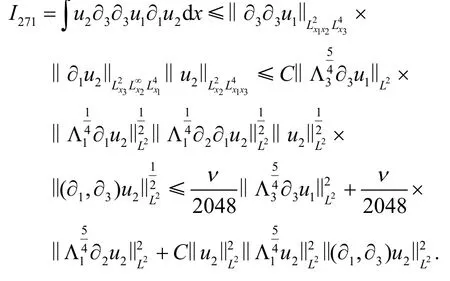
类似地,
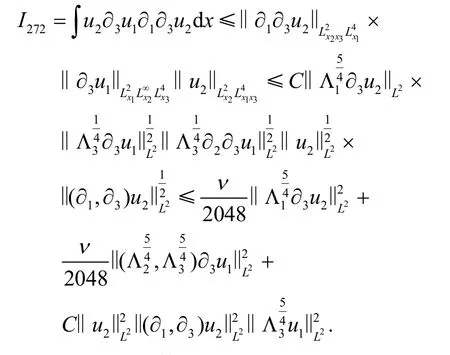
因此就完成了I27的估计.
现在转向I28和I29.通过分部积分和散度条件∇·u=0得
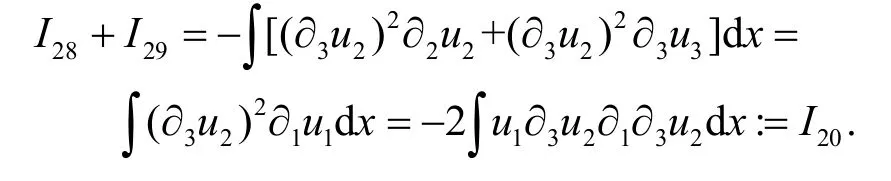
对I20的估计与I21类似.因此可得
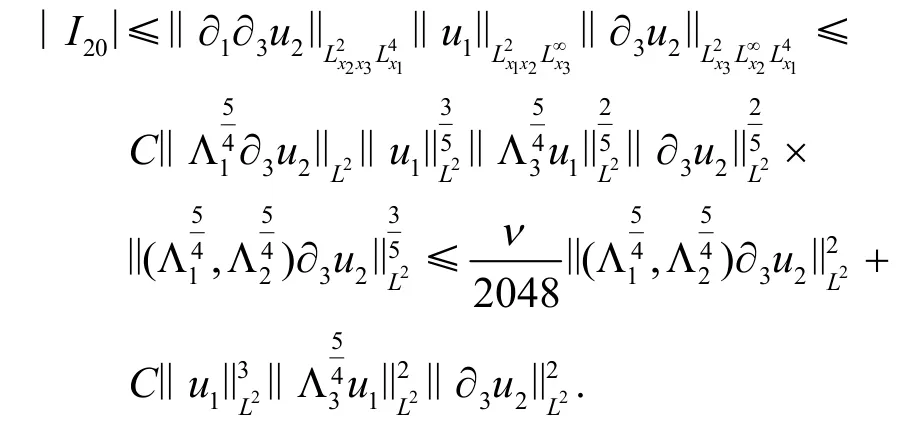
这就完成了I2的估计.
现在考虑I3.注意 ∂3u3出现在I3的许多项中,通过散度条件可以将其转换为 -(∂u11+∂2u2).更准确地说,
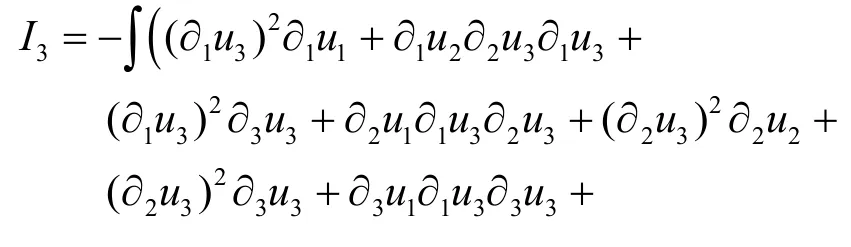

将方程(14)中的项根据它们出现的顺序依次标记为I31,I32,…,I39.
首先处理I31.
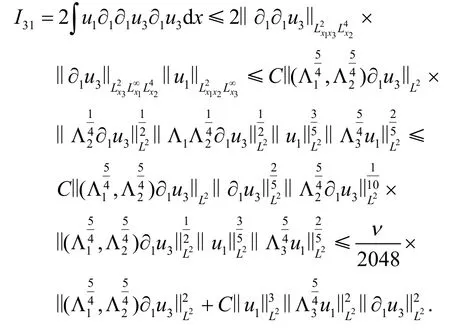
通过分部积分有
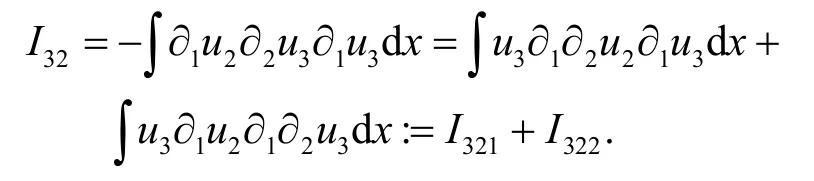
对I321的估计与I22的估计类似,因此有
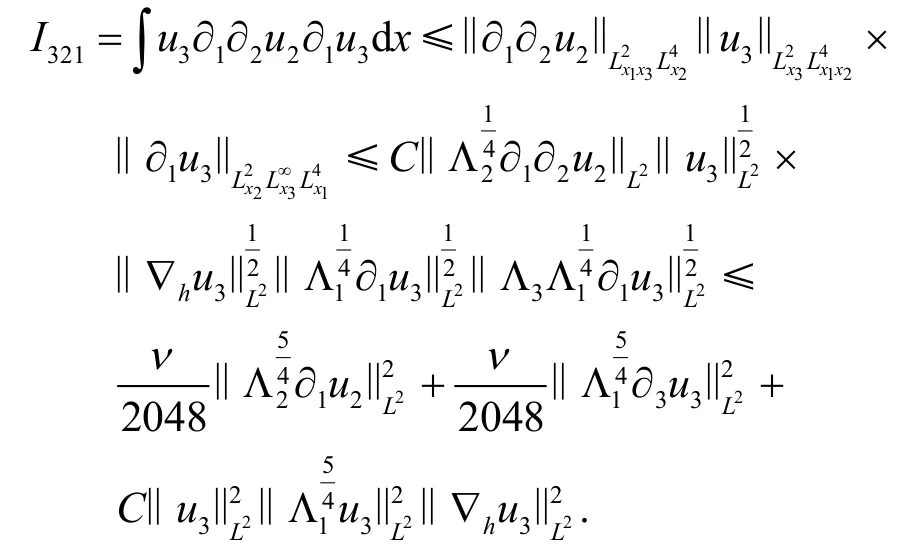
类似地,
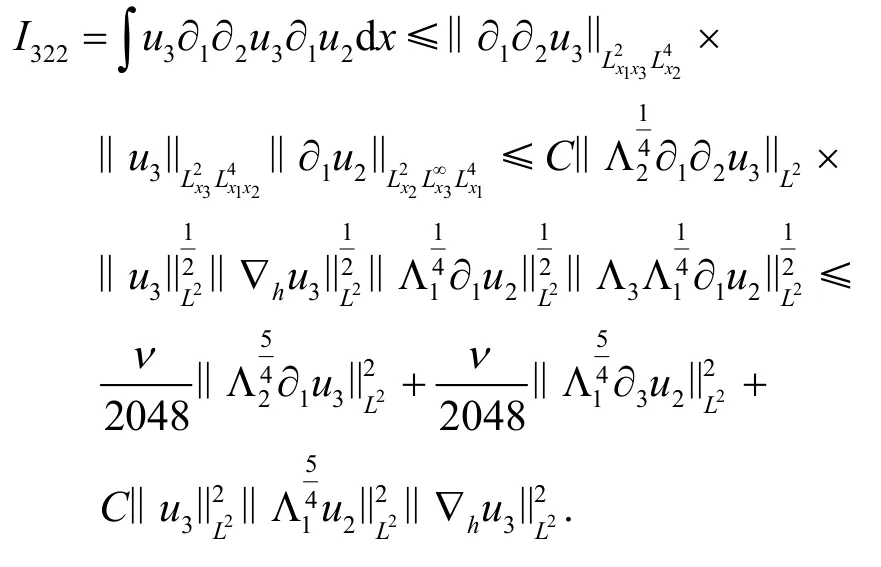
用估计I321的方法去估计I33得

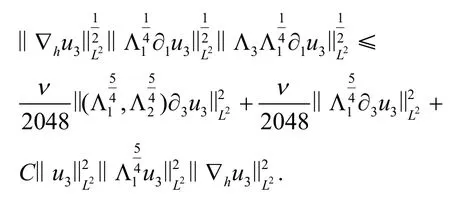
通过分部积分可得
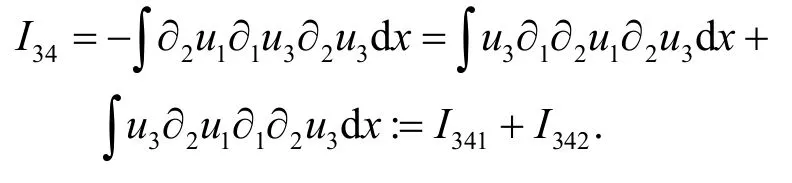
对I341的估计跟I331的估计方法类似,因此有
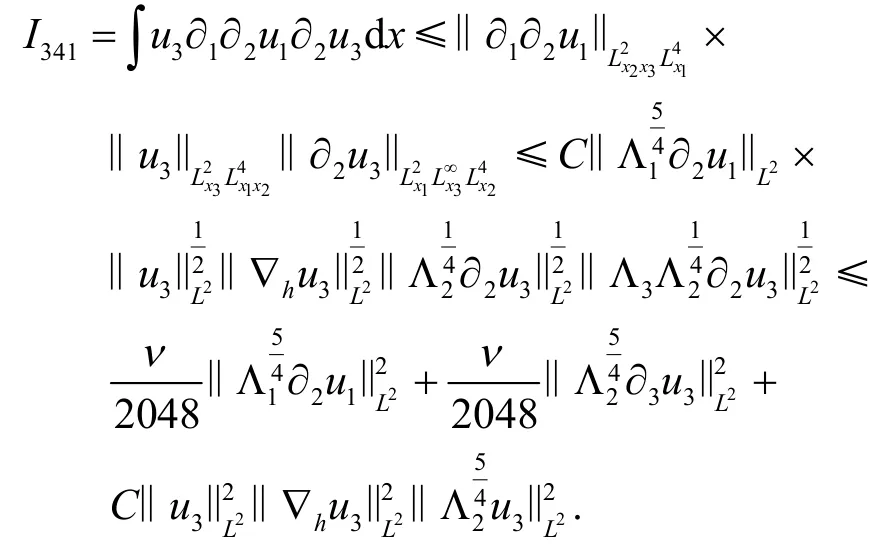
同理得
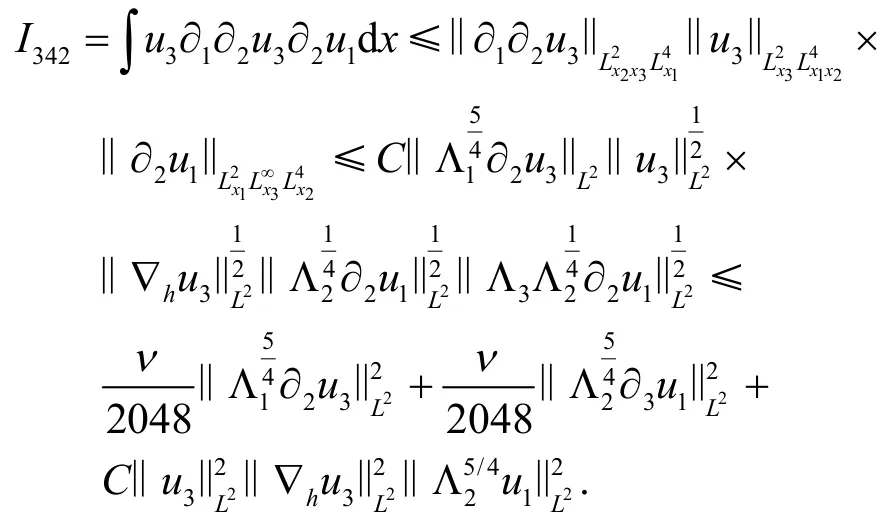
现在转向I35和I36.根据分部积分和散度条件∇·u=0有
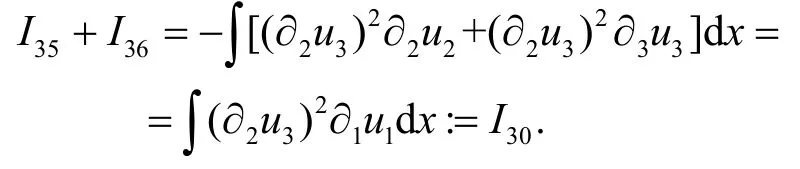
通过分部积分可得
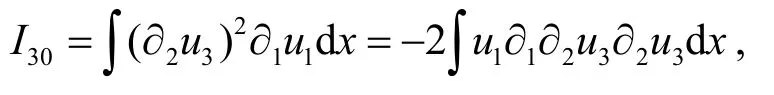
因此有
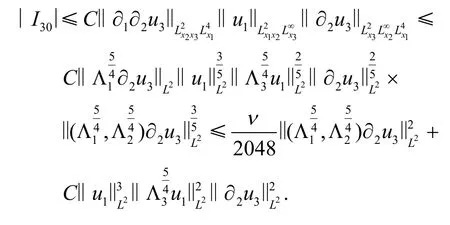
考虑I37,通过分部积分得
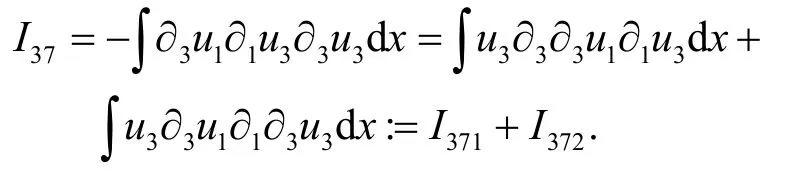
事实上,
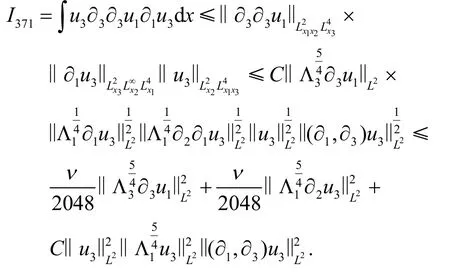
类似地,
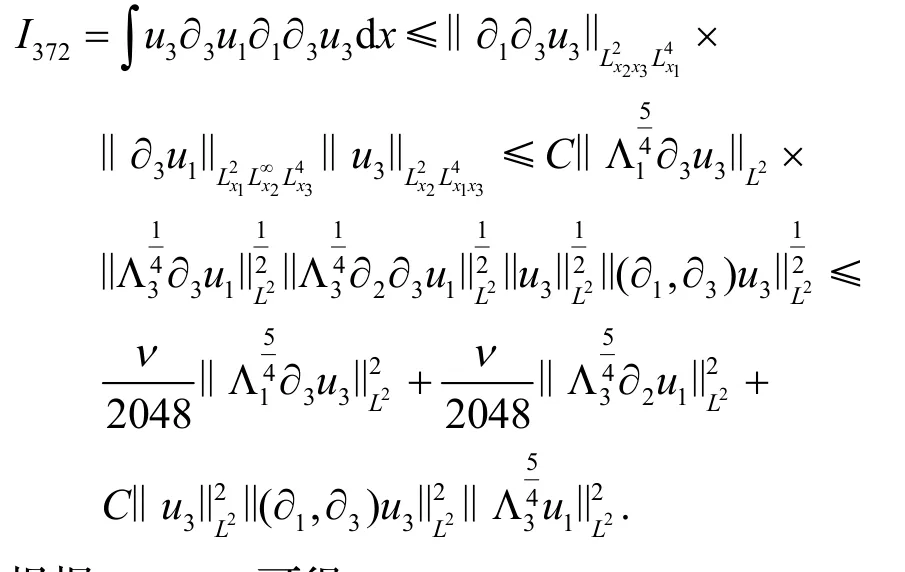
根据∇·u=0可得

用分部积分可以计算出
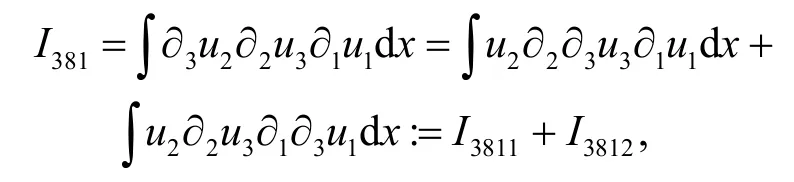
其中

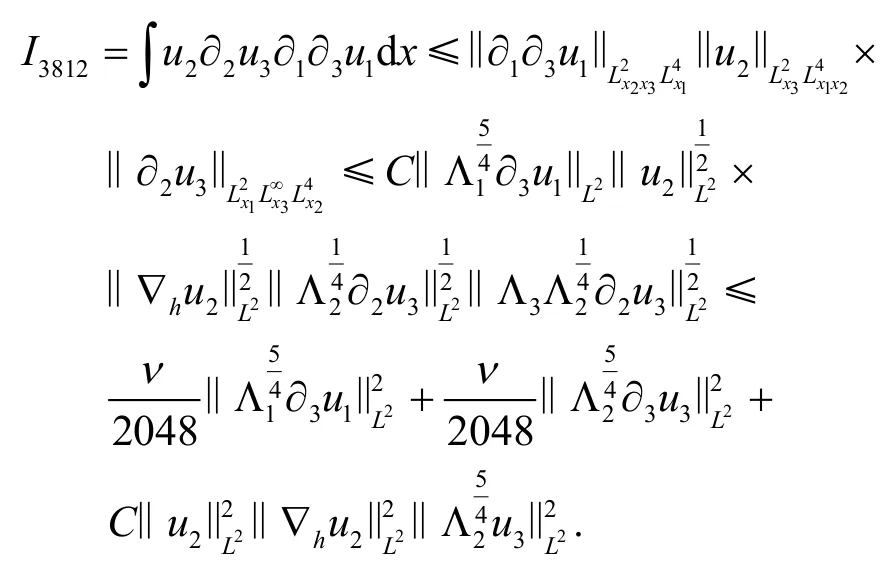
由于I382=-I22,因此省略.
根据散度条件 ∇·u=0,可以计算出
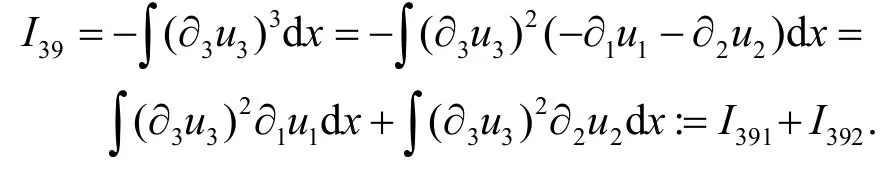
因此
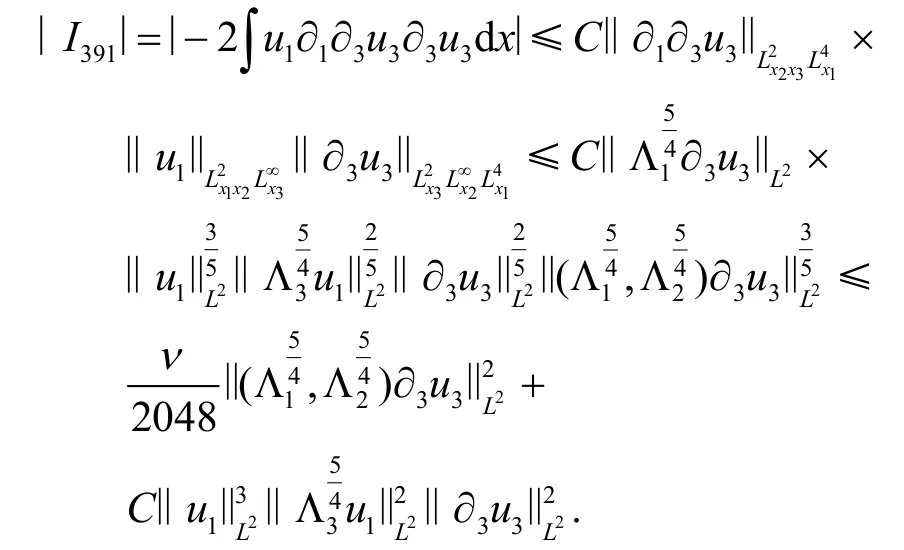
利用散度条件∇·u=0可以得到
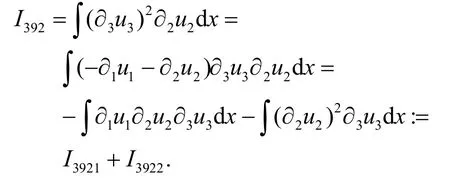
由分部积分可得
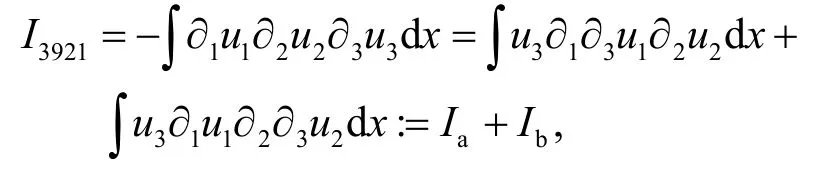
因此
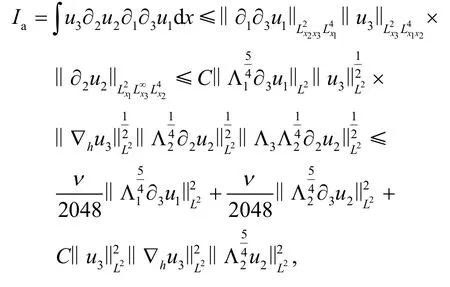
同理得
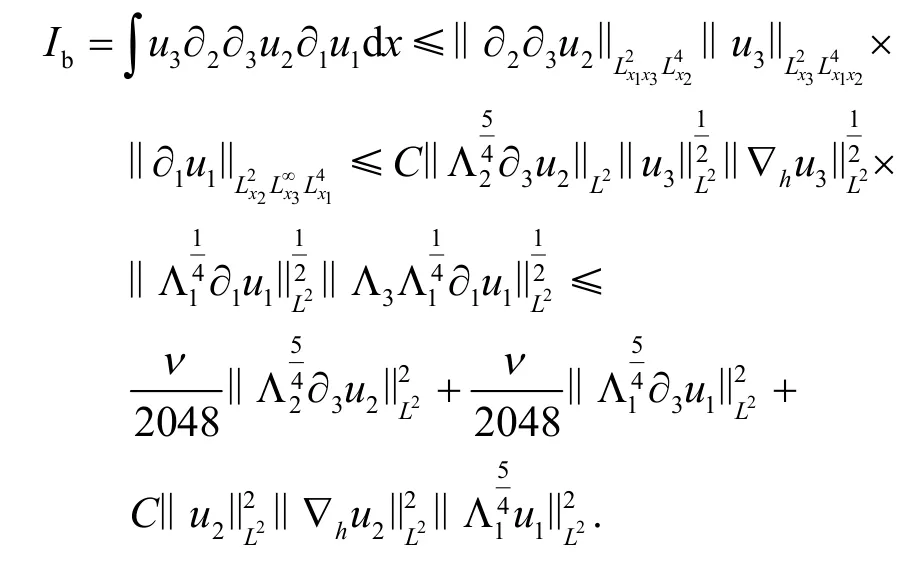
根据I342的估计,可以得到
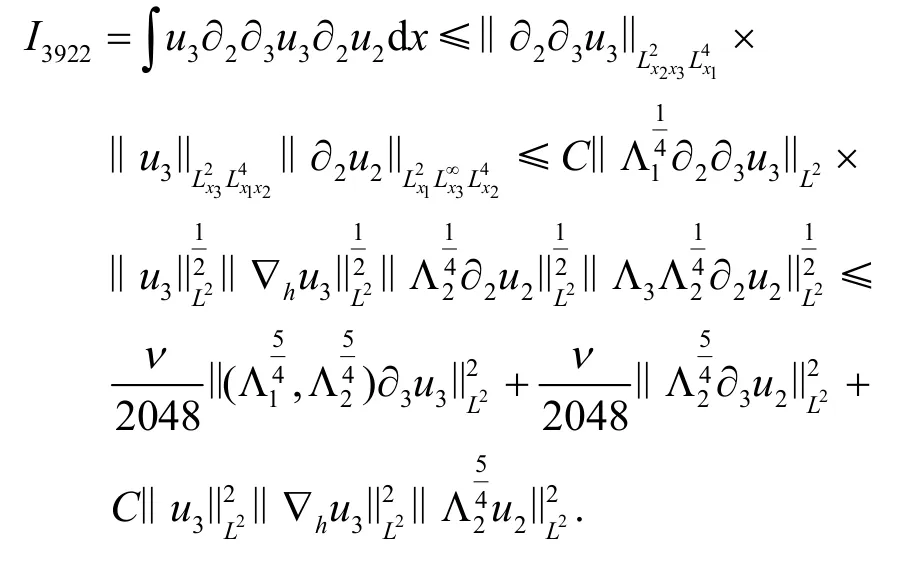
正如之前提到的,u1包含三个方向的扩散,因此I1的估计比I2和I3更简单,故在此省略了相关计算.将上述所有估计综合在一起得到
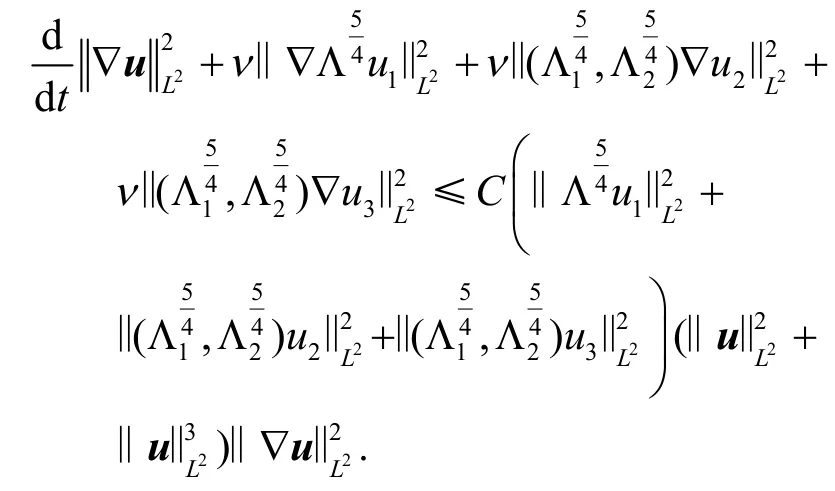
通过Grönwall 不等式可知

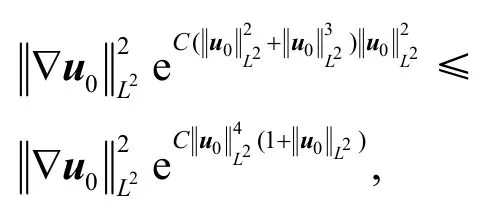
则全局存在性和正则性成立.
3 唯一性的证明
本节证明定理2 中的唯一性结果.

则其满足


由Hölder 不等式和引理1 得
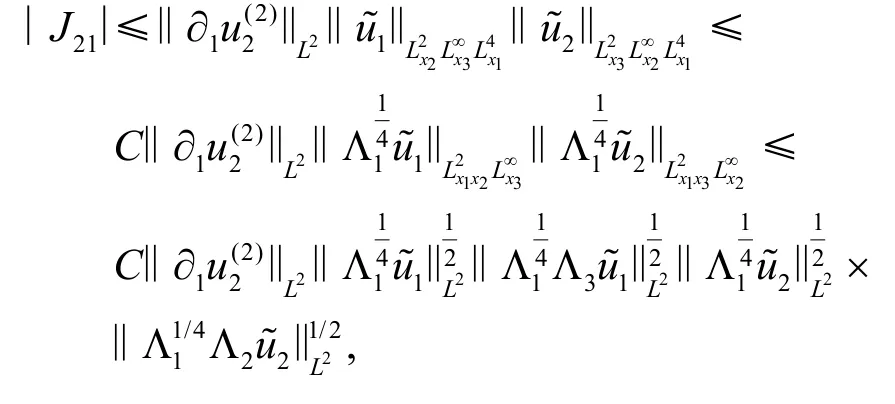
其中使用了插值不等式
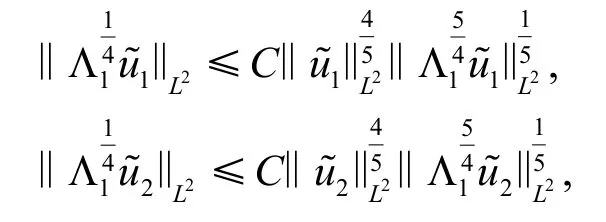
从而
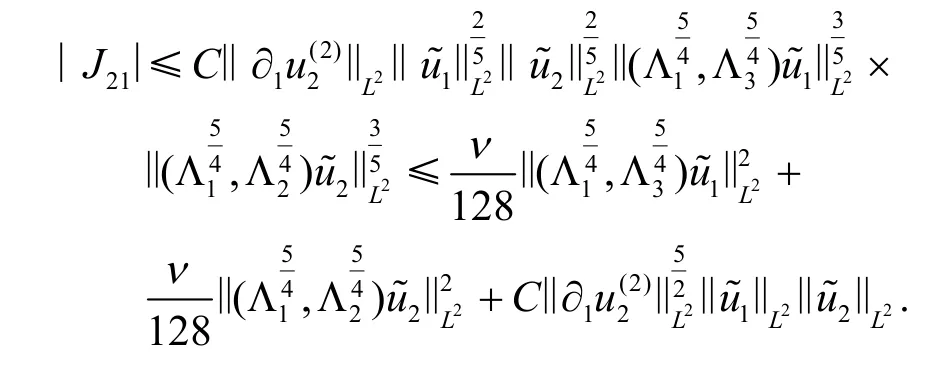
类似地,

结合J1,J2和J3的估计得


