融合黄金正弦算法和纵横交叉策略的秃鹰搜索算法

赵沛雯，张达敏*，张琳娜，邹诚诚

（1.贵州大学 大数据与信息工程学院，贵阳 550025；2.贵州大学 机械工程学院，贵阳 550025）

0 引言

为了解决较为复杂的工程问题，大量群智能算法被相继提出。群智能算法是指一类受生物群体行为启发而设计的具有分布式智能行为特征的智能算法。目前已有的群智能算法包括模拟退火（Simulated Annealing，SA）算法［1］、鸡群算法（Chicken Swarm Optimization，CSO）［2］、鲸鱼优化算法（Whale Optimization Algorithm，WOA）［3］、蝗虫算法（Grasshopper Optimization Algorithm，GOA）［4］等。

秃鹰搜索算法（Bald Eagle Search optimization algorithm，BES）是马来西亚学者Alsattar 等［5］在2020 年提出的一种新颖的、受自然启发的元启发式优化算法，通过模拟秃鹰在狩猎鱼类时的智能社会行为。与其他智能算法相比，BES 具有较强的全局搜索能力，能够有效地解决各类复杂数值优化问题。但是，BES 存在易陷入局部最优、多样性差等问题，尤其是在解决较为复杂的多峰函数问题上缺点更加明显。目前，对于标准BES 的这些缺点，贾鹤鸣等［6］提出将莱维（Levy）飞行策略与模拟退火机制引入BES，增强局部搜索与全局收敛能力，同时将改进的BES（Improved BES，IBES）用于优化支持向量机（Support Vector Machine，SVM）学习器，并将这种融合模型应用于封装式特征选择。实验结果表明，IBES 能够改善SVM 的性能，提高SVM 的效率和数据的分类精确度。

为了使算法加快收敛的同时能够跳出局部最优，本文引入了纵横交叉策略（crisscross strategy）［7］以及黄金正弦算法（Golden Sine Algorithm，Gold-SA）［8］，并对搜索阶段的位置公式进行重新定义，提出一种融合黄金正弦算法和纵横交叉策略的秃鹰搜索算法（BES with Golden Sine algorithm and Crisscross strategy，GSCBES）。实验结果表明，GSCBES 具有能够平衡全局搜索和局部搜索能力，并且在收敛速度和精度方面均有所提升。使用GSCBES 对反向传播（Back Propagation，BP）神经网络模型［9］的权值和阈值进行寻优，并将优化的BP 神经网络模型用于空气质量的预测，实验结果表明，预测精确度较优化前有所提高。

1 秃鹰搜索算法

秃鹰遍布于北美洲地区，飞行中视力敏锐，观察能力优秀。以捕食鲑鱼为例，秃鹰首先会基于个体和种群到鲑鱼的浓度来选择搜索空间，朝一个特定区域飞行；其次，在选定搜索空间内搜索水面，直到发现合适的猎物；最后，秃鹰会逐渐改变飞行高度，快速向下俯冲，从水中成功捕获鲑鱼等猎物。秃鹰搜索算法模拟秃鹰在狩猎过程中的行为，以证明狩猎各阶段的协同序列是合理的。相应地，该算法可以分为三个部分，即选择搜索空间、在选择的搜索空间内搜索和俯冲。

1.1 选择阶段

在选择阶段，秃鹰在选定的搜索空间内识别并选择最佳区域（食物量大的区域），在该区域内它们可以捕食猎物。式（1）从数学上呈现了这种行为。

其中：α∈[1.5，2]是控制位置变化的参数；r为区间（0，1）的一个随机数；Pbest表示秃鹰当前根据最佳位置选择的搜索空间被识别；Pmean表示秃鹰之前搜索的所有位置的平均分布；Pi表示第i只秃鹰的位置。

1.2 搜索阶段

在搜索阶段，秃鹰在选定的搜索空间内搜索猎物，并在螺旋空间内向不同方向移动以加速搜索。螺旋飞行数学模型采用极坐标方程进行位置更新，具体计算公式如下：

其中：a∈(5，10) 表示中心点与搜索点之间的夹角；R∈(0.5，2)表示搜索周期数；θ(i)和r（i）分别为螺旋方程的极角与极径；rand为（0，1）的一个随机数；x（i）与y（i）表示极坐标下的秃鹰位置，取值均为（-1，1）。由此可得到在极坐标下秃鹰位置更新的公式：

其中：Pi+1为秃鹰下一次的位置。

1.3 俯冲捕食阶段

俯冲捕食阶段，秃鹰从搜索空间的最佳位置摆动到目标猎物，所有的搜索点也向最佳点移动。该运动同样也使用极坐标的方式进行描述，具体计算公式如下：

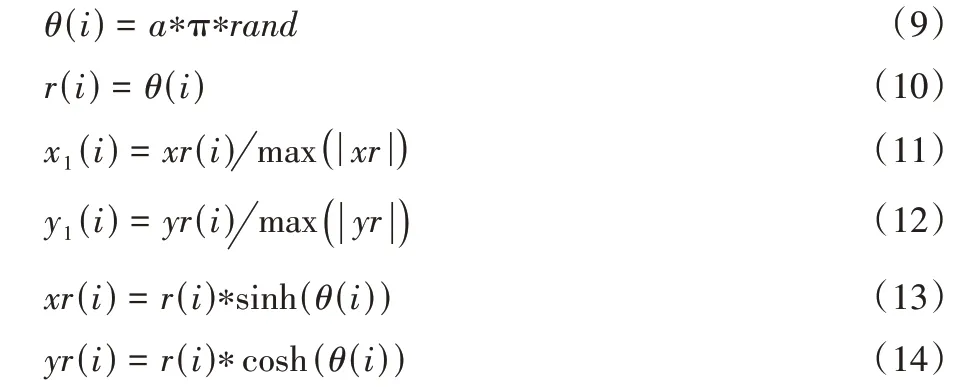
由此可得到秃鹰捕食猎物的位置更新公式为：

其中：c1和c2均为区间［1，2］的随机数，用于增加秃鹰向最佳点和中心点移动的强度。

2 本文算法

为了克服BES 收敛速度慢、精确度不高等缺点，本文对搜索阶段的秃鹰位置更新公式设置权重并引入纵横交叉策略对秃鹰搜索算法进行改进。

2.1 纵横交叉策略

秃鹰搜索算法的空间选择阶段，主要利用随机搜索的先验信息乘以α来更新位置，然后在前一个搜索区域附近选择另一个不同的搜索区域，此时若前一个搜索区域已经成为局部最优，那么下一次的搜索就会陷入局部最优造成“早熟”，导致算法收敛精度降低。为了防止秃鹰个体“早熟”，本文在个体俯冲捕食阶段之后引入了纵横交叉策略［7］，该策略能够提高解决复杂优化问题的全局搜索能力，从而提高收敛速度和求解精度。

2.1.1 水平交叉

水平交叉指对两个不同秃鹰之间在所有维度上操作的算术交叉，使不同个体之间能够相互学习，增大全局搜索能力，防止种群过早收敛，从而提高收敛速度和搜索精度。在执行水平交叉策略之前，将秃鹰个体两两不重复地设置为父代个体X（i）和X（j），并以交叉概率Ph进行算术交叉，为了尽可能多地找到解决方案，通常交叉概率设置为1。父代交叉后通过式（16）～（17）产生子代个体：

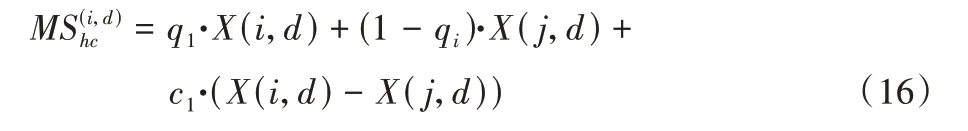
其中：q1、q2均为［0，1］的随机数；c1和c2均为［-1，1］的随机数；X（i，d）、X（j，d）分别表示为第d维的父代X（i）和X（j）；分别表示X（i，d）和X（j，d）通过水平交叉产生的第d维子代。生成的子代与父代之间进行竞争，最终保留最优个体。

2.1.2 垂直交叉

标准BES 在迭代后期易陷入局部最优，往往是因为种群在更新过程中某些个体在某一维度陷入局部最优所造成的。垂直交叉是在两个不同维度之间对所有个体进行运算的算术交叉，在整个迭代过程中，垂直交叉搜索的父种群来自水平交叉的优势解的种群，能够防止种群陷入局部最优；同时每个垂直交叉操作只产生一个子代，以便为停滞维度提供跳出局部最优的机会，而不破坏另一个可能是全局最优的维度。对个体i的第d1维和第d2维进行垂直交叉，通过式（18）得到后代个体：

其中：q为［0，1］上的随机数：为父代X（i）在第d1维和第d2维进行垂直交叉产生的子代。垂直交叉产生的子代个体与父代进行竞争，保留适应度较优的个体。

2.2 基于惯性权重的位置更新

在标准的粒子群优化（Particle Swarm Optimization，PSO）算法［10］中，对于位置更新方程，目前较多采用线性递减权值（Linearly Decreasing Weight，LDW）策略，通过引入动态权值ω获得比固定值更好的寻优结果。

其中：tmax为最大迭代次数；ωini为惯性权重初始值，ωend为惯性权重最终值。

受此启发，本文提出一种基于惯性权重的秃鹰位置更新公式，用于更新搜索阶段的位置公式，赋予秃鹰能够调整全局和局部搜索的能力，以提高标准BES 的性能。

其中：b1∈[0，1]为群体交流系数；b2∈[0，1]为个体记忆系数；通常ωini取0.9，ωend取0.4。

2.3 黄金正弦捕食机制

黄金正弦算法（Golden-SA）［8］是一种数学启发算法，该算法是受正弦的启发构建的。在该算法中，随机个体的数量与每个维度上均匀分布的搜索代理的数量相同。在Golden-SA的位置更新中引入了黄金分割系数，黄金分割能够缩小搜索范围，只在能够产生最优解的空间进行搜索，从而提高了算法的收敛速度，使算法具有较强的局部开发能力。受文献［11］启发，本文将Golden-SA 作为局部算子引入到俯冲捕食阶段的位置更新公式中，使算法的寻优空间更全面，提高算法的寻优速度以及求解精度。同时利用Golden-SA 中的r1、r2参数能够缩小搜索空间，指引秃鹰个体快速向种群最优个体靠近，降低算法陷入局部最优的可能性。具体的位置更新公式如下：

其中：r1为［0，2π］的随机数；r2为［0，π］的随机数；x1=-π+(1-τ)*2π，x2=-π+τ*2π 是根据黄金分割系数τ（τ=而得到的系数。这些系数缩小了搜索空间，允许当前值接近理想值。

2.4 算法步骤

综上所述，GSCBES 的步骤如下：

Step1 设置GSCBES 的相关参数：种群规模N，最大迭代次数tmax，搜索维度dim，搜索范围ub、lb。

Step2 计算种群中每个秃鹰个体的适应度值，并根据目标函数值的大小排序，标记出全局最优值Pbest。

Step3 根据全局最优值Pbest的位置进行搜索空间的选择，同时利用式（1）进行位置更新。

Step4 选取完搜索空间之后使用螺旋移动搜索，秃鹰个体在搜索空间搜索猎物，利用式（21）进行位置更新。

Step5 秃鹰俯冲捕食，利用式（22）进行位置更新。

Step6 引入纵横交叉策略，防止算法陷入局部最优。

Step7 判断是否达到结束条件，如果达到则输出最优结果，否则重复步骤Step2～6。

3 实验与结果分析

为了更加全面地验证本文算法性能，同时验证每个改进策略的有效性，本文的仿真实验分为5 个部分：

1）将GSCBES 与标准BES［5］以及IBES［6］比较，通过对比实验分析GSCBES 的有效性和可行性；

2）将GSCBES 与基于惯性权重位置更新的GSCBES1、融入黄金正弦算法的GSCBES2、结合纵横交叉策略的GSCBES3 进行对比，以验证不同改进策略的可行性；

3）将GSCBES 与 模拟退火（SA）算 法［3］、粒子群优化（PSO）算法［10］、融合精英反向和纵横交叉的WOA（Elite opposition-based and Crisscross optimization for WOA，ECWOA）［12］进行比较，以验证GSCBES 的优越性；

4）通过Wilcoxon 秩和检验验证GSCBES 与其他算法之间的显著性差异；

5）通过在CEC2014 基准函数中选取部分单峰、多峰、混合复合类型的函数进行优化测试，以验证GSCBES 的可行性和鲁棒性。

3.1 实验设置

为了验证本文提出的GSCBES 的性能，本文选取如表1所示的11 个Benchmark 函数作为实验对象，其中，f1～f7为单峰函数，f8～f11为多峰函数。单峰函数用于测试算法的收敛速度和收敛精度；多峰函数由于具有多个局部极值，常用来测试算法跳出局部最优的能力以及全局搜索的能力［13］。在进行仿真实验之前，为了使实验结果具有公正性和客观性，将所有算法的规模设置为30，最大迭代次数为1 000。GSCBES、BES、IBES、ECWOA、PSO 以及SA 的其他相关参数设置如表2 所示。

表1 11个测试函数Tab.1 Eleven test functions

表2 不同算法的参数设置Tab.2 Parameter setting of different algorithms

3.2 与标准BES比较

将标准BES 与GSCBES 在空间位数dim=30 的条件下对11 个测试函数进行求解，并通过最优值、平均值、标准值以及单词运行耗时t指标评估算法效能。表3 为算法在11 个测试函数上独立运行30 次的结果。

标准差反映了算法的稳定性和鲁棒性，而平均值则反映了算法收敛速度。如表3 所示，在单峰函数f1～f7中，对于函数f1～f4，GSCBES 除了能寻到函数理论最优值0 之外，平均值和标准差也均为0，表明相较于BES，GSCBES 具有更高的收敛精度且寻优结果稳定；对于函数f5和f7，GSCBES 虽没有寻到理论值0，但不论是平均值还是标准差均优于标准BES，由此可得GSCBES 具有更高的寻优精度且寻优结果更稳定；对于函数f6，虽未寻到理论值，但与标准BES 相比，平均值相差21个数量级，标准差相差20 个数量级，这些均表明GSCBES 能够得到更优的结果且收敛速度明显提升。

在多峰函数f8～f11中，对于函数f8，与标准BES 相比，GSCBES 具有较优的稳定性；对于函数f10～f11，GSCBES 虽没有寻到理想最小值，但与BES 相比，具有更高的收敛精度和寻优结果的质量，其中f10的标准值为0，表明GSCBES 具有更高的稳定性；对于f9，GSCBES 寻到理想最小值。

总之，对于11 个测试函数，相较于标准BES，GSCBES 具有更高的全局搜索能力和鲁棒性，能够跳出局部最优。

从表3 中还可以看出，不论是单峰函数还是多峰函数，GSCBES 单次运行的时间均比标准BES 长，这是由于在BES中引入本文提出的3 种改进策略后，算法搜索区域更广，找到的解更多，从而导致算法寻优时间变长，但在其余3 项指标方面，GSCBES 均有明显提高。

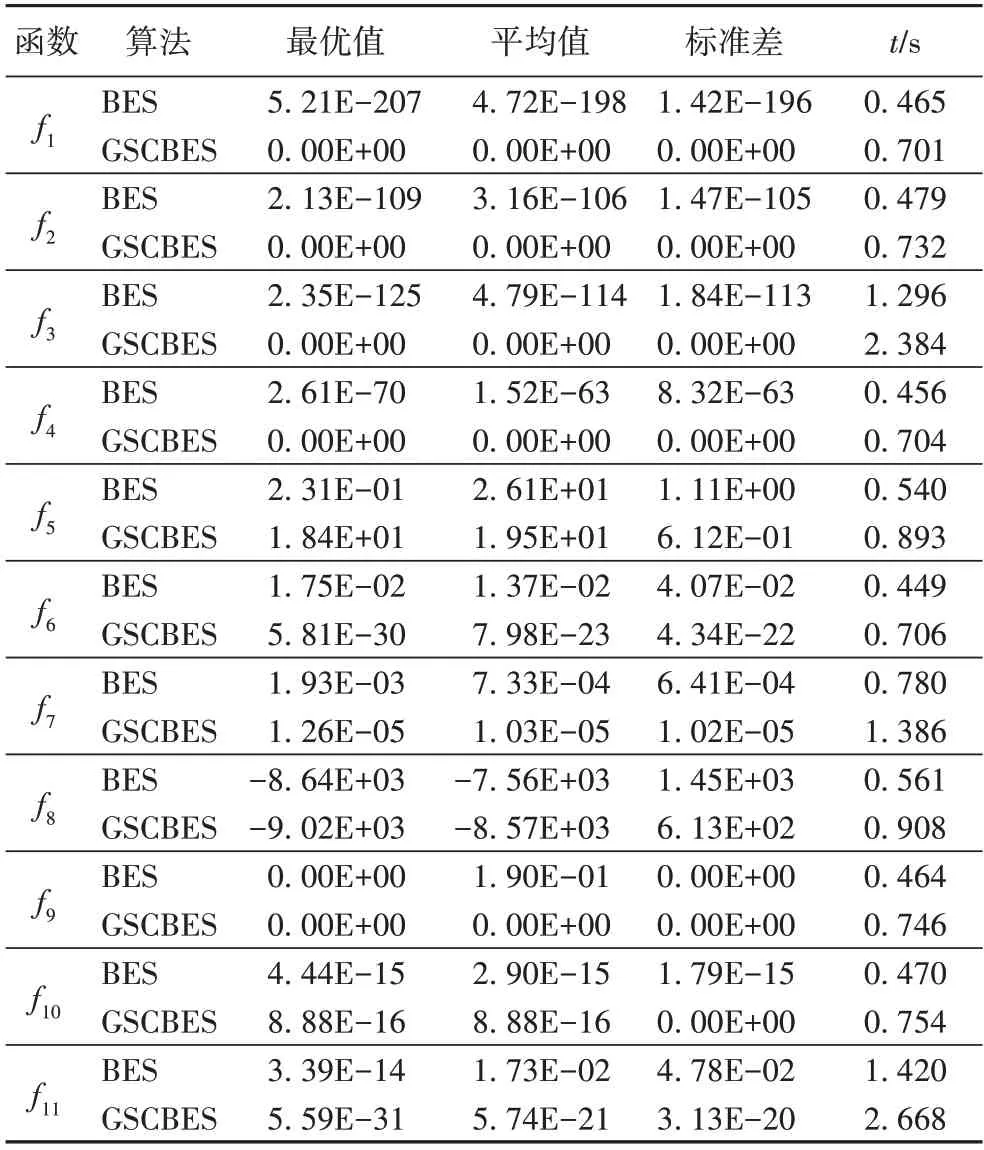
表3 GSCBES与BES测试结果的比较Tab.3 Comparison of GSCBES and BES test results

3.3 不同改进策略比较

将GSCBES 与基于惯性权重位置更新的GSCBES1、融入黄金正弦算法的GSCBES2、结合纵横交叉策略的GSCBES3进行对比，进一步验证不同策略的可行性。算法参数与3.2节相同。表4 为算法独立运行30 次的仿真结果。

由表4 可知，对于f1～f4，GSCBES 的最优值、平均值与标准差均能够达到理论值；对于函数f5～f7，GSCBES 不论是在寻优精度还是速度等方面均有显著提升；对于f8，虽然GSCBES 在其他项指标未优于标准BES，但在标准值方面有所提升，表明GSCBES 在稳定性方面优于标准BES。

具体地，GSCBES1 和GSCBES2 对于函数f1～f4、f6的有效性有显著影响，从最优值、平均值与标准差可以看出，基于惯性权重位置更新的改进策略和融入黄金正弦算法的改进策略能够有效地提高算法寻优能力以及收敛精度；对于函数f9和f12，这两种改进策略均提高了算法跳出局部最优的能力。GSCBES3 对于函数的寻优结果是3 种改进策略中效果较差的，但其在收敛精度方面相较于标准BES 也得到了提升，尤其对于函数f8，在稳定性方面有更显著的优化。从表4 的仿真结果来看，无论在单峰函数还是多峰函数中，融入3 种改进策略的GSCBES 有效地提高了收敛速度、收敛精度以及稳定性。

表4 不同策略的结果比较Tab.4 Comparison of results of different strategies

从单次运行耗时上来看，相同维度下，基于惯性权重位置更新的GSCBES1 比标准BES 耗时短，表明加入惯性权重之后增加了算法全局搜索能力；而融入黄金正弦算法的GSCBES2 和结合纵横交叉策略的GSCBES3 均比标准BES 耗时长，这是因为在标准BES 中分别加入这两种策略后，找到的解更多，从而导致寻优时间变长。

为了从多样性的角度验证改进策略的有效性，图1 给出了标准BES、GSCBES 和3 种改进策略在相同维度dim=30 条件下的收敛曲线。从图1 可以看出，无论是单峰函数还是多峰函数，GSCBES 都具有较高的收敛速度和收敛精度。其中：图1（a）～（c）为单峰函数的收敛曲线，可以看出GSCBES1和GSCBES2 具有更高的收敛精度以及更快的寻优速度，GSCBES3 是3 个改进策略中寻优效果较差的，但其寻优精度同样比BES 高；图1（d）～（f）为多峰函数的收敛曲线，可以看出，3 种改进策略算法的收敛曲线均在BES 的收敛曲线之下，且下降快，说明改进算法在相同维度下的收敛速度和收敛精度均有显著提高。综上所述，以上3 种改进策略对标准BES 的收敛性、鲁棒性等方面均有显著影响。

图1 不同改进策略下的收敛曲线对比Fig.1 Comparison of convergence curves under different improvement strategies

3.4 与其他群智能算法的比较

将GSCBES 与SA［3］、PSO［10］、IBES［6］、ECWOA［12］进行比较，分别在dim=10，30，200 的条件下对11 个测试函数进行寻优，独立运行30 次的结果如表5 所示。由表5 可知，相同维度下，PSO 的单次运行耗时最短，ECWOA 和SA 次之，GSCBES 第三，IBES 耗时最长。这是因为同PSO、SA 以及ECWOA 相比，GSCBES 在基本算法中加入了3 种改进策略之后，算法的搜索范围扩大，寻找到的解增多，导致寻优时间变长。加入惯性权重后提升了算法全局搜索能力，从而使算法的收敛速度得到提高。虽然PSO 在单次运行耗时上最短，但其寻优精度同SA 相差不大，且两者的寻优结果相对较差。ECWOA 和IBES 的收敛精度是4 种对比算法中较高的，但GSCBES 的收敛速度和稳定性明显优于其他4 种算法。

表5 各群智能算法在不同维度下的结果比较Tab.5 Comparison of results of different swarm intelligence algorithms in different dimensions

从纵向数据来看，PSO 的寻优效果最差；SA 次之；而ECWOA 只对f9求解时才能达到理论值，IBES 只对函数f1、f3和f9求解时能够寻到理论值；虽然对于函数f5和f9，GSCBES的寻优结果并不是最好的，但其相较于其他函数不仅在收敛速度方面有所提升，同时也提高了算法稳定性，尤其是f1～f4、f9，不仅能寻到理论值，同时稳定性方面也有明显的提升。

从横向数据来看，当维度dim从10 到30 再到200，对于函数f1～f3、f7，除ECWOA 外，其他算法的求解精度均有所下降，这是由于随着维度的增加，函数复杂度也增加，从而寻优时需要做更多的调整，然而GSCBES 的寻优结果仍然是最优。

对于f4、f6，算法的求解精度和稳定性均有所提升，但相较于4 种对比算法，GSCBES 不论是求解精度还是稳定性都是最高的。对于f5，随着维度的增加，5 种算法的寻优能力均有所提升，虽然GSCBES 的寻优结果没有IBES 好，但其在耗时上低于IBES，表明本文算法的全局搜索能力以及收敛速度比IBES 更优。对于f8，PSO 的收敛速度优于GSCBES，但其稳定性和鲁棒性不如GSCBES；虽然IBES 的标准差优于GSCBES，但其耗时远多于GSCBES。对于f9，所有算法的收敛速度和鲁棒性随着维度的增加均有所下降，但相较于4 种比较算法，GSCBES 的求解精度仍然最高。对于f10，除ECWOA 外，其余4 种算法不论是求解速度还是稳定性方面均有所上升，其中GSCBES 和IBES 的平均值和标准差虽一样，但在耗时上GSCBES 比IBES 短，表明在保证寻优结果的同时GSCBES 能够快速跳出局部最优。对于f11，除ECWOA和SA 外，其余算法的求解精度均有所上升，其中GSCBES 不论是稳定性还是寻优能力均是最优的，从而验证了GSCBES在低维和高维条件下均有更好的求解能力。

3.5 Wilcoxon秩和检验

为了检验本文算法与其他算法之间是否有显著的区别，验证本文算法的稳定性，使用Wilcoxon 秩和检验用作非参数统计检验以确定结果，其决定了两个样本之间的差异。假设H0：两种算法之间没有明显区别；H1：两种算法之间有明显区别。当检验结果R＜0.05 时，拒绝零假设，此时说明算法之间有显著的区别；当检验结果R＞0.05 时，接受零假设，此时说明算法之间并无显著的区别。

表6 为在相同维度dim=30 的条件下，GSCBES 与其他算法对比的秩和检验结果。其中“R”表示检验结果；“W”为显著判断结果；由于最佳算法不能与自身进行比较，故表6 中标记为“NA”，即表示无法进行显著性的判断；“+”表示GSCBES 比其他算法更具显著性；“-”表示GSCBES 的寻优能力低于其他算法；“=”表示GSCBES 与其他算法的性能并无明显的差异。

表6 Wilcoxon秩和检验结果Tab.6 Results of Wilcoxon rank sum test

从表6 可以看出，绝大部分的R 远小于0.05，相应的W值为“+”。因此，总体上GSCBES 与其他8 种算法间具有显著性差异，表明GSCBES 对于其他算法具有更高的显著优势，即有更好的寻优能力。

3.6 CEC2014基准函数上测试

为了进一步验证GSCBES 的稳定性和鲁棒性，本文在CEC2014 测试函数中选取部分单峰函数（Unimodal Function，UM）、多峰函数（Multimodal Function，MF）、混合函数（Hybrid Function，HF）和复合函数（Composition Function，CF）进行优化求解。选取的部分函数如表7 所示，本文实验种群规模为30，迭代次数为1 000，维度30。

表7 CEC2014测试函数Tab.7 CEC2014 test functions

表8 整理了部分CEC2014 测试函数独立运行30 次后各算法的平均值和标准差。由于CEC2014 函数具有复杂的表征特征，因此所有算法都较难寻到函数最优值［14］。由表8 可知，对于CEC01，与GSCBES1 相比，GSCBES 的稳定性略差，但其收敛速度最优。对于多峰函数，相较于PSO，GSCBES 的平均值略差，但其稳定性和鲁棒性方面最优。在混合和复合函数中，GSCBES 的寻优结果更接近理论值，且稳定性方面也是最优的，表明GSCBES 具有良好的有效性和鲁棒性。

表8 不同算法在CEC2014测试函数上的优化结果比较Tab.8 Comparison of optimization results of different algorithms on CEC2014 test functions

4 基于GSCBES的BP神经网络模型

BP 神经网络模型是目前使用频率较高的一种神经网络模型，根据误差来进行反向传播。但在传统BP 神经网络模型中，网络的阈值和初始权重值随机产生，使BP 存在易陷入局部最优的缺陷，这会对预测结果的精确度有所影响［15］。针对这一缺陷，本文通过引入融合黄金正弦算法和纵横交叉策略的秃鹰搜索算法GSCBES 初始化网络模型的权值和阈值，从而提高BP 神经网络模型的精确度，并将优化的BP 神经网络模型用于空气质量的预测。

4.1 初始化工作

本文使用的数据源于加州大学欧文分校（University of California Irvine）提出的用于机器学习的数据库中针对部署在意大利城市现场的气体多传感器设备的每小时的平均响应记录和气体浓度［16］。选择数据前1 900 个样本作为训练集，后100 个数据作为测试集，并对提取到的数据集采用最大最小法［17］进行归一化处理。

由于过多的隐含层会使网络结构过于复杂，导致计算量增加，所以研究中常选用三层网络，即只含有单层隐含层［18］。在构建BP 神经网络模型的结构中，隐含层节点数的确定对网络性能有很大的影响，若节点数太少，网络获取的有用信息就少；若节点数过多，不仅增加训练时间，还可能出现过拟合的现象，使网络的泛化能力下降［19］。因此本文利用经验式（23）来确定隐含层节点数。

其中：N为隐含层节点数；m为输入层节点数；n为输出层节点数；a∈[1，10]，为常数。

为了检验不同隐含层节点数下网络模型的性能，本文使用均方误差（Mean Square Error，MSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）这两项指标进行仿真评估。其中MSE 是一种衡量“平均误差”的常见方法，能够确定数据的离散程度，均方差误差越小，则表明预测模型可以获得更好的精度；MAPE 指的是所有单个观测值和真实值的绝对偏差百分比，与比例无关，可用于不同比例的预测［20］。表9 为不同节点数下网络的MSE 和MAPE，由表9 可以看出，节点数为4 时，MSE 和MAPE 均取得了最小值，因此，最终得到2-4-1 的网络结构。

表9 不同隐含层节点数下的预测误差Tab.9 Prediction errors under different hidden layer node numbers

在构建完网络结构之后，需要对网络进行参数设置。其中，学习率lr通常取值为0～1，在神经网络传播中帮助网络避免陷入局部极小，找到全局最小值；然而学习率设置过低会使网络训练速度慢，过高则会使网络出现过拟合现象［18］。本文比较了隐含层节点数为4 时，不同学习率和精确度下的预测误差，结果如表10 所示。由表10 可知，学习率和精确度均取0.01 时的预测误差值较小。最后利用GSCBES 初始化BP 神经网络模型的阈值和权值，从而提高网络结构的精确度和收敛速度。

表10 不同学习率及精确度下的预测误差Tab.10 Prediction errors at different learning rates and accuracies

4.2 神经网络模型仿真与分析

图2 为基于GSCBES 的BP 神经网络模型（GSCBES-BP）与原始BP 神经网络模型（以下简记为BP）、基于PSO 的BP（PSO-BP）的误差比较结果。通过图2 可直观地看出，相较于原始BP，GSCBES-BP 利用GSCBES 得到的最优个体来初始化BP 神经网络的阈值和权值，同时将MSE 作为秃鹰个体的适应度值，克服了原始BP 神经网络由于随机初始化权重和阈值而导致的精确度不高、易陷入局部最优等缺陷。同时由于GSCBES 中引入了黄金正弦算法和纵横交叉策略，使算法能够跳出局部最优，从而提高收敛速度和精度，这也使GSCBES-BP 经过训练之后得到的误差要小于PSO-BP 的误差。

图2 3种神经网络模型的预测误差对比Fig.2 Comparison of prediction errors of three neural network models

为了更全面地说明GSCBES-BP 优于原始BP 和PSO-BP，本文还使用平均绝对误差（Mean Absolute Error，MAE）和均方根误差（Root Mean Square Error，RMSE）进行对比。其中MAE 是一种线性分数，所有个体差异在平均值上的权重都相等，不存在误差之间正负抵消的问题，比平均误差更能表明预测值的真实水平；RMSE 对极大或极小误差十分敏感，可以很好地反映预测的精确度［21］。表11 为原始BP、PSO-BP以及于GSCBES-BP 在4 种指标下的仿真结果。由于GSCBES提高了收敛速度和精度，并且能够跳出局部最优值，它的4项指标值均小于PSO-BP；并且，由于GSCBES-BP 是将最优个体作为模型的初始化权值和阈值，使模型的预测精度得到提高，因此它的4 项指标的值均优于原始BP，同时也表明本文提出的优化方式效果较好。

表11 GSCBES-BP、PSO-BP与BP的结果对比Tab.11 Comparison of results of GSCBES-BP，PSO-BP and BP

5 结语

本文在标准秃鹰搜索算法的基础上引入新的基于惯性权重的位置更新公式、纵横交叉策略以及黄金正弦算法，提出改进的秃鹰搜索算法GSCBES，它能够跳出局部最优，具有平衡全局搜索和局部搜索能力。通过实验结果可以看出，GSCBES 在求解精度和收敛速度上都明显优于对比算法SA、IBES、PSO 和ECWOA，同时提升了算法的稳定性和鲁棒性。将GSCBES 应用于初始化BP 神经网络的权值和阈值，同时对空气质量进行预测，实验结果表明，基于GSCBES-BP 的神经网络模型预测的均方误差等结果均明显优于PSO-BP 和BP 神经网络模型。在后续的研究中，计划将改进算法应用到通信系统的频谱分配问题中，进一步验证CSCBES 算法的性能。