Stochastic Analysis for the Dynamics of a Poliovirus Epidemic Model

Ali Raza,Dumitru Baleanu,Zafar Ullah Khan,Muhammad Mohsin,Nauman Ahmed,Muhammad Rafiq and Pervez Anwar

1Department of Mathematics,Government Maulana Zafar Ali Khan Graduate College Wazirabad,Punjab Higher Education Department(PHED),Lahore,54000,Pakistan

2Department of Mathematics,Cankaya University,Balgat,Ankara,06530,Turkey

3Department of Medical Research,China Medical University,Taichung,40402,Taiwan

4Institute of Space Sciences,Magurele-Bucharest,077125,Romania

5Department of Dermatology,Rashid Latif Medical College Lahore,Lahore,54000,Pakistan

6Department of Mathematics,Technische Universitat Chemnitz,Chemnitz,6209111,Germany

7Department of Mathematics and Statistics,The University of Lahore,Lahore,54590,Pakistan

8Department of Mathematics,Faculty of Science and Technology,University of Central Punjab,Lahore,54000,Pakistan

9Department of Biochemistry,University of Sialkot,Sialkot,51311,Pakistan

ABSTRACT Most developing countries such as Afghanistan, Pakistan, India, Bangladesh, and many more are still fighting against poliovirus. According to the World Health Organization, approximately eighteen million people have been infected with poliovirus in the last two decades.In Asia,still,some countries are suffering from the virus.The stochastic behavior of the poliovirus through the transition probabilities and non-parametric perturbation with fundamental properties are studied.Some basic properties of the deterministic model are studied,equilibria,local stability around the stead states,and reproduction number.Euler Maruyama,stochastic Euler,and stochastic Runge-Kutta study the behavior of complex stochastic differential equations. The main target of this study is to develop a nonstandard computational method that restores dynamical features like positivity,boundedness,and dynamical consistency. Unfortunately, the existing methods failed to fix the actual behavior of the disease. The comparison of the proposed approach with existing methods is investigated.

KEYWORDS Poliovirus model;differential equations;methods;analysis

1 Introduction

Jenkins et al. in 2006 formulated a model in which he concluded that the use of monovalent is better than other vaccines.It provides outstanding outbreak control[1].Haldar et al.[2]introduced the poliovirus vaccine in India. Kalkowska et al. in 2020 represent a differential equation-based stochastic model for poliovirus transmission.The model shows the poliovirus transmission for 2019 to 2023 with a strategic eradication plan[3].Minor studied the types of polioviruses,vaccination,and eradication of the virus worldwide [4]. Thompson [5] investigated the transmission dynamics of the poliovirus in Nigeria.Duque-Marin et al.[6]studied two types of vaccines in the mathematical model.Denes et al.[7]presented a model which describes polio transmission in tropical regions.Cheng et al.[8]discussed a polio vaccination model in two different age classes.Alba et al.[9]addressed the correlation between climate and vaccination through a mathematical model. Shaghaghi et al. in 2018, studied that the OPV and IVPPvs vaccine was helpful for the eradication of the virus last few years [10].Shimizu in 2014 [11] explained IPV is very effective against the poliovirus, and the author reviewed the introduction,development,and characterization of the OPV vaccine.In addition,his place in the world was told.Rafique et al.in 2020 presented a mathematical model in which they discovered the dynamics of poliovirus transmission using standard methods with vaccination [12]. Nidia et al. [13]in 2007, examined the effects of the poliovirus on human life and the steps taken to eradicate the virus and discussed what steps we could take in the future to get rid of it. Thompson et al. [14]presented polio outbreaks in the USA. Kalkowska et al. introduced a model to identify poliovirus and opportunities to increase population immunity[15].Kim et al.[16]presented a model to examine the transmission of virulent circulating vaccine-derived polioviruses. Hillis [17] formulated a model in different regions before using artificial poliovirus vaccination.Mendrazitsky et al.[18]explained a disease of epidemic development model. The model analyzed other properties of polio and its nonequilibrium outbreak dynamics.Debanne et al.[19]presented a mathematical model of poliovirus in America. Naik et al. [20,21] studied the fractional modeling of cancer and HIV infection with the well-known results of stabilities.

The strategy of the paper is as follows. The first section goes to literature, and Section 2 goes to stochastic modeling of poliovirus and its fundamental properties. Section 3 goes to the proposed numerical method and its simulation with current approaches in the literature.Section 4 goes to the paper’s conclusion and remarks.

2 Poliovirus Model

For any timet,S:represents the class that is influenced by infection,E:represents the class that is disclosed by infection,I:represents an infective class,V:represents immunization class,A:represents the constant immigration rate of the human population.β:is the per unit time probability of infection transmission by the infective population.r:is the reduction in the exposed class due to transmission of infection.v:represents the proportion of recruits in the susceptible class moving to the vaccinated class,v1:is the number of vaccinated exposed populations,b:number of exposed populations moving to the infection class.μ:natural death of the human population,α:disease death rate.The first order,nonlinear,and coupled ordinary differential equations of the poliovirus epidemic model are assumed as follows:

with initial condition S(0)≥0;E(0)≥0;I(0)≥0;V(0)≥0,and(σi:i=1,2,3,4)is the peutrbation term withB(t)is the Brownian motion[22,23].

2.1 Properties[24]

This section studies the positivity and boundedness of the system ((1)-(4)). Let us consider the vector as follows:

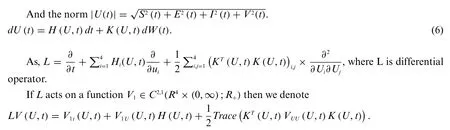
where transportation is denoted byT.

Theorem 1:For model((1)-(4))and any given initial value(S(0),E(0),I(0),V(0))∈R4+,there is a unique solution(S(t),E(t),I(t),V(t))ont≥0 and will remain inR4+with probability one.

Proof:By Ito’s formula, the model ((1)-(4)) admits a positive solution in the unique local on[0,τe],and explosion time is denoted byτe.Because the local Lipschitz condition is satisfied by all the coefficients of the model as mentioned earlier.

Next, let us show that the given model ((1)-(4)) admits this solution in the global sense; that is,τe=∞almost sure.

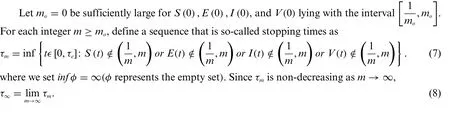
Thenτ∞≤τe.To prove,τ∞=∞.

In case of violation of statement,thenT ＞0 andε ∊(0,1)such that

this,there is an integerm1＞m0such that

Define aC4-functionV:→R+by

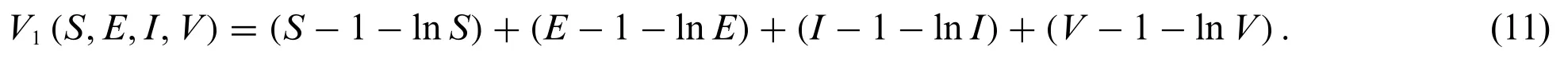
By using Ito’s formula,we calculate

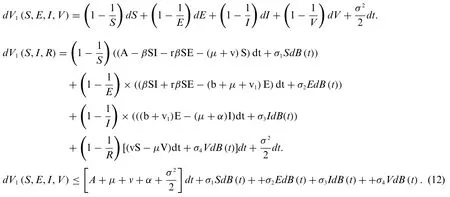
Let,N=A+μ+v+α+Then Eq.(12)could be written as

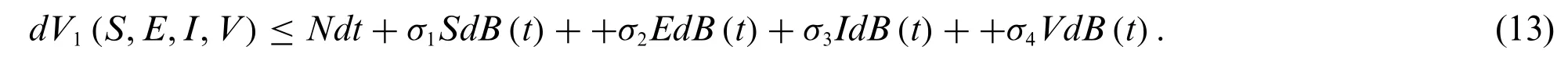
By integrating from 0 toτm∧τ,we get

whereτm∧τ=min(τm,T),the taking the expectations to lead to

Set Ωm= {τm≤T}form ＞m1,and from(15),we haveP(Ωm≥ε).For everyv∈Ωmthere are someisuch thatui(τm,v)equals eithermorfori=1,2,3;

Hence,V1(S(τm,v),E(τm,v),I(τm,v),V(τm,v))is less than min

Then we obtain

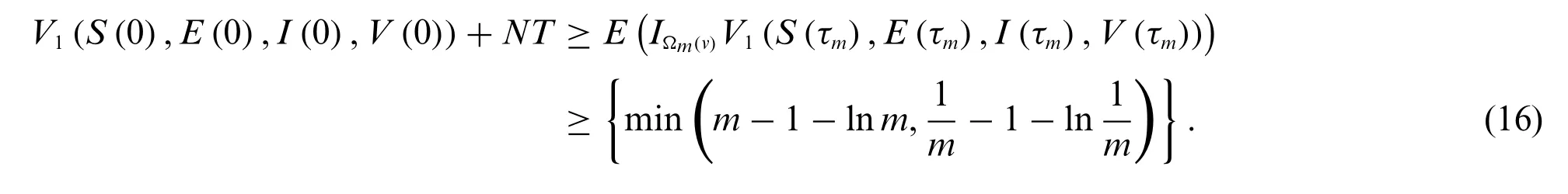
IΩm(v)of Ωmrepresents the indicator function. Lettingm→∞leads to the contradiction ∞=V1(S(0),E(0),I(0),V(0))+NT ＜∞.

As desired.

2.2 Equilibria of Model

The disease-free equilibrium of the model is K0=

The endemic equilibrium of the model is denoted by K1=(S*,E*,I*,V*).

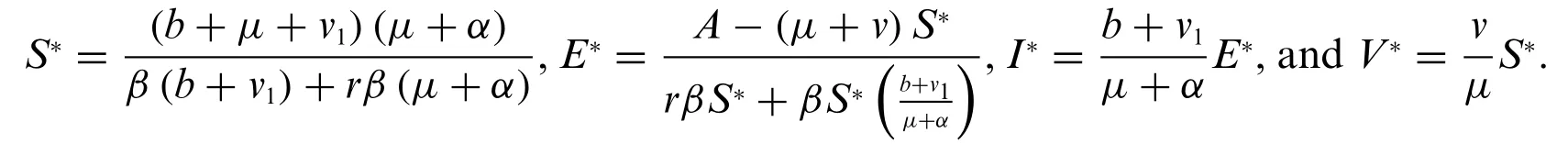
2.3 Local Stability of Model

Theorem 2:The disease-free equilibrium K0=is locally asymptotically stable ifR0＜1;otherwise,unstable ifR0＞1.

Proof:Considering the function from the system((1)-(4))as follows:

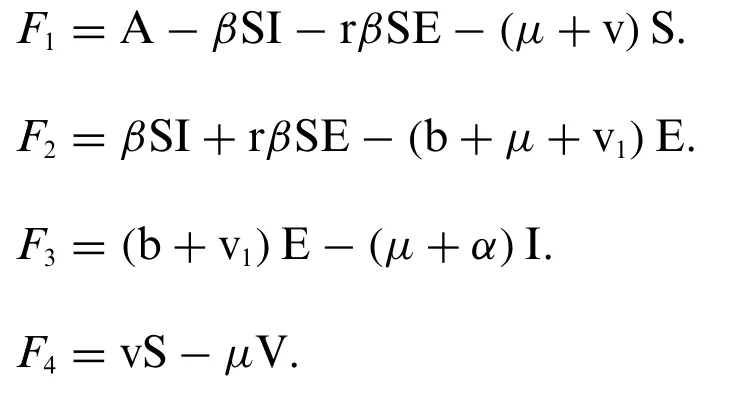
The elements of the given Jacobean Matrix atKOis as follows:

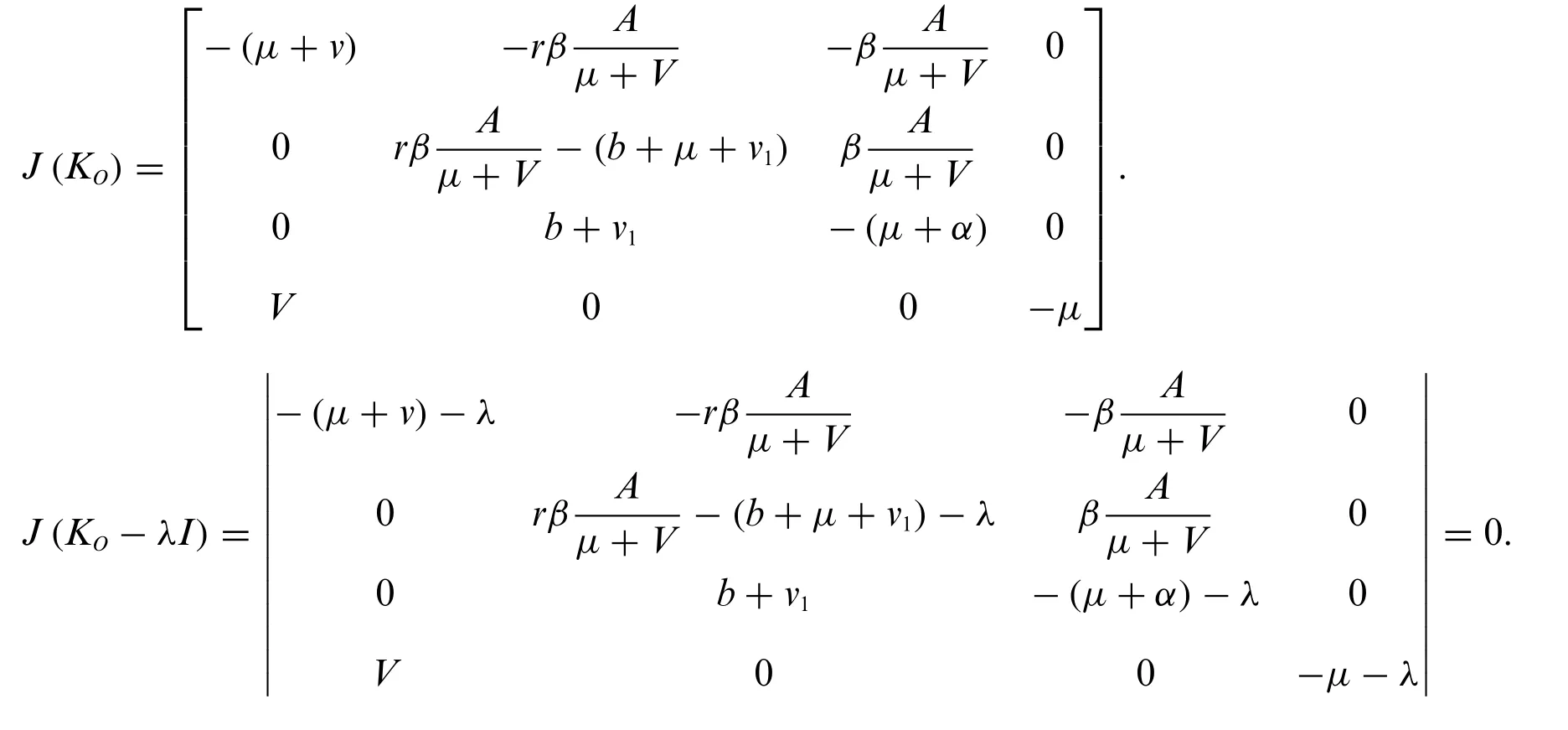
We obtain the following results by applying Routh Hurwitz criteria for 2ndorder.

A1＞0,A2＞0, ifR0,R2＜1, whereA1= [(μ+α)+(b+μ+v1)(1-R2)],A2=(μ+α)(b+μ+v1)(1-R0).

Theorem 3:The endemic equilibrium K1= (S*, E*, I*, V*) is locally asymptotically stable ifRo ＞1.

Proof:The Jacobean matrix at K1=(S*,E*,I*,V*)is as follows:

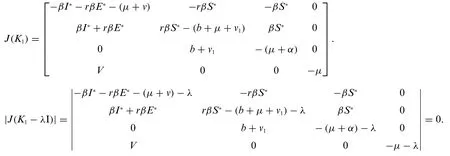
Applying Routh-Hurwitz Criterion for 3rd order,A ＞0,D ＞0,andAC ＞D,ifR0＞1.

Hence the given system is locally asymptotically stable.

2.4 Reproduction Number

The idea of reproduction number is presented in[25]by considering Eqs.(3)and(4),we get the following matrices:

The spectral radius of theFG-1is called the reproduction number is as follows:

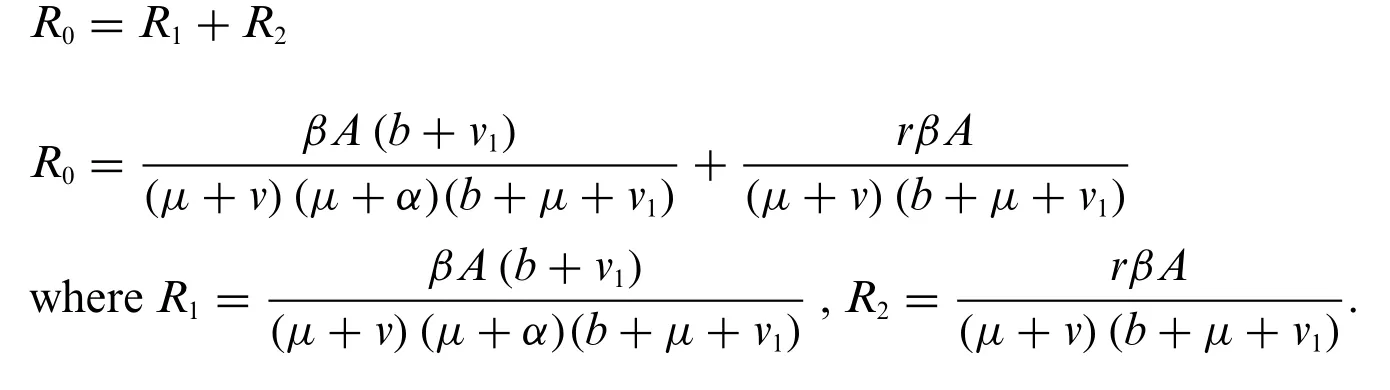
3 Stochastic Poliovirus Epidemic Model

Let us consider the vector C = [S,E,I,V]Tof stochastic differential equations (SDEs) of the poliovirus epidemic model((1)-(4)).We want to calculate the expectation and variance(see Table 1).

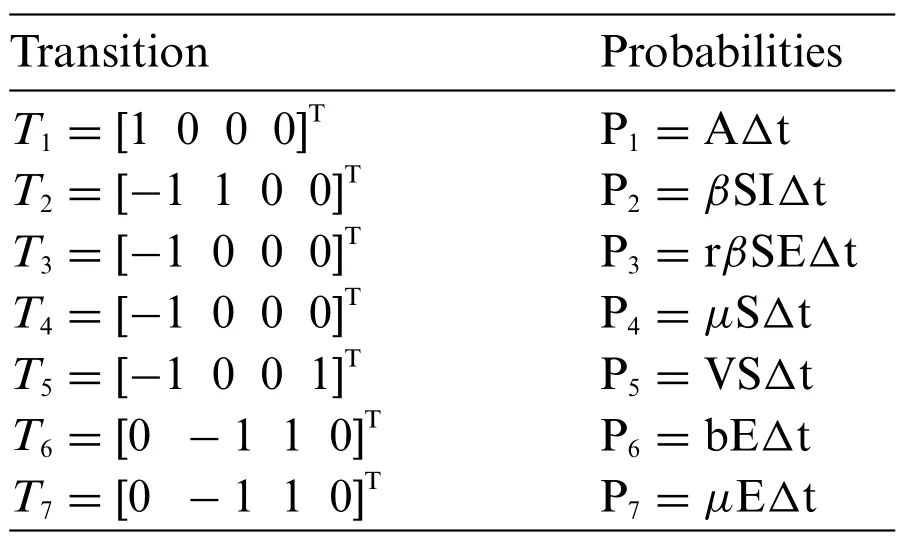
Table 1: Transition probabilities of polio epidemic model

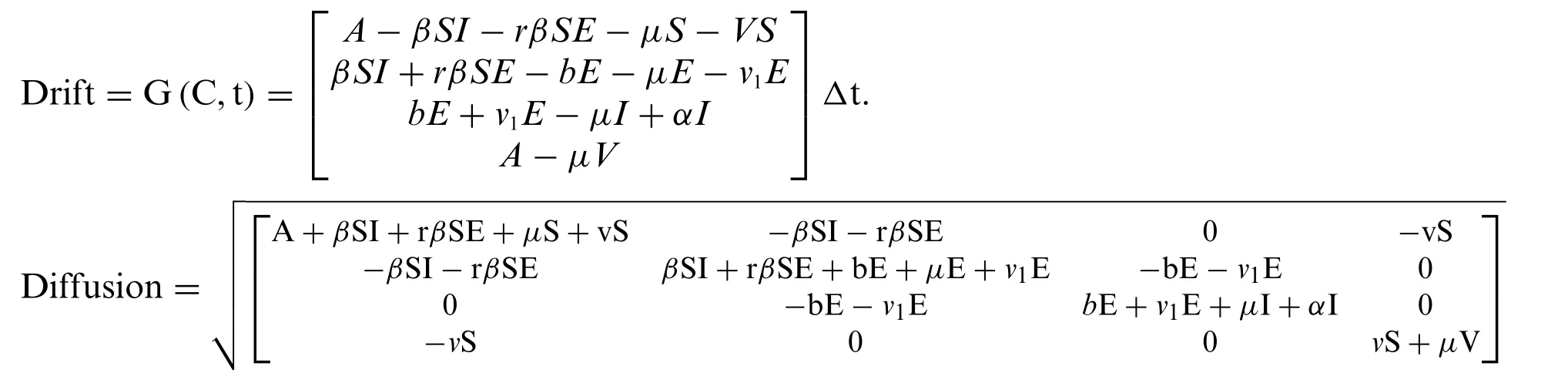
The equation of poliovirus epidemic model((1)-(4))can be written as

The Euler Maruyama approach is cast-off to determine the numerical result of the Eq.(17) by using the values of the parameters given in Table 2 as follows:

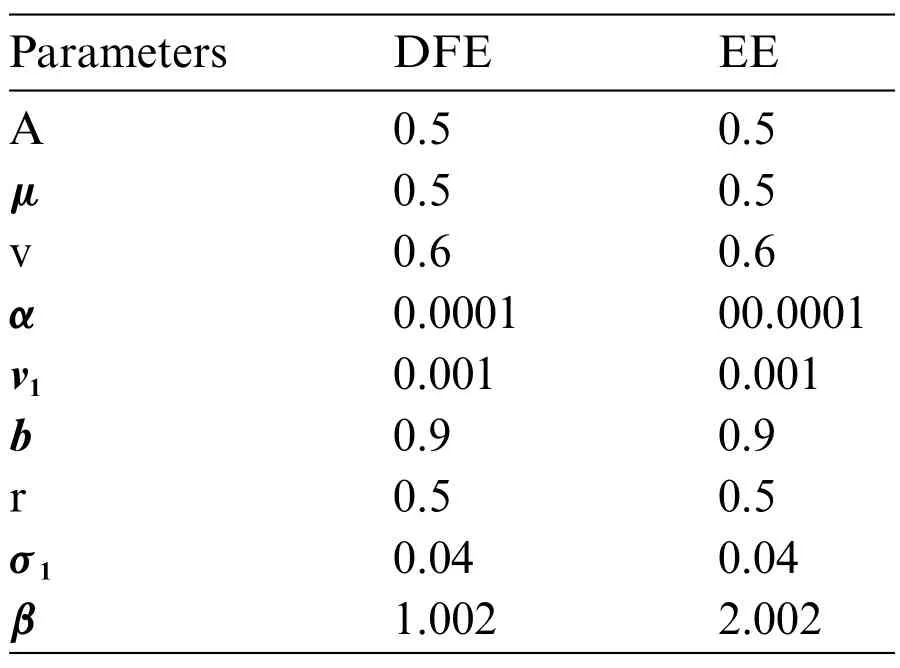
Table 2: Values of parameter[26]

Cn+1=Cn+f (Cn,t)Δt+L(Cn,t)dB.

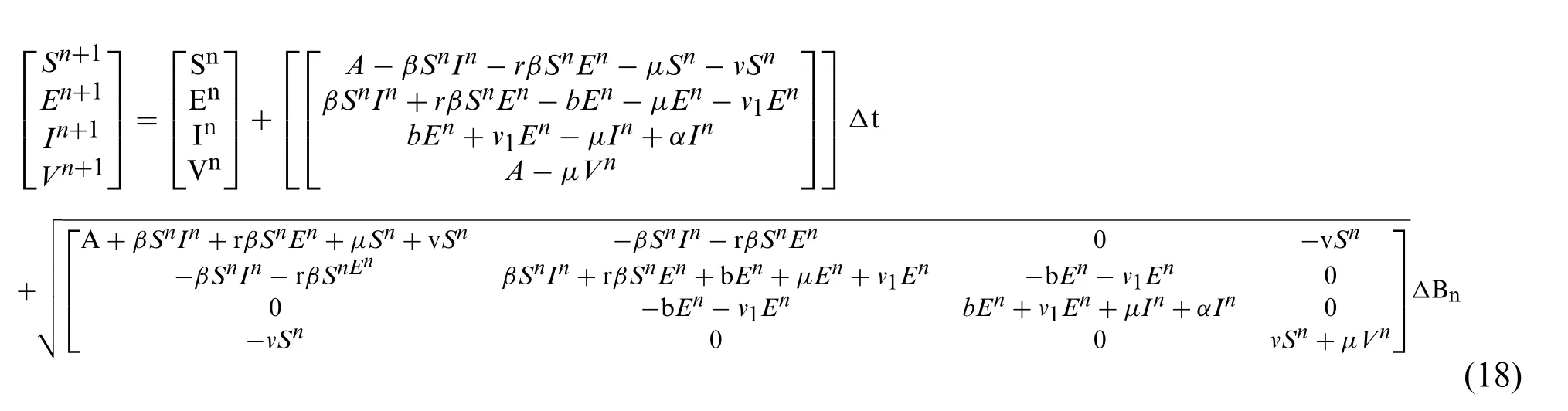
where C(0)=Co=[0.5,0.3,0.2,0.1,]T,0 ≤t ≤C and Brownian motion is denoted asB.

3.1 Stochastic Nonstandard Finite Difference Method

The stochastic NSFD can be developed for the system((1)-(4))as

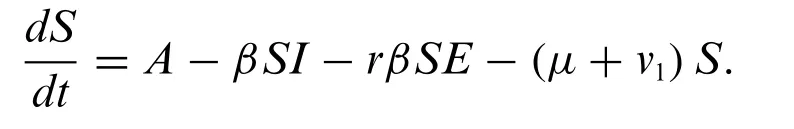
The breakdown of the proposed method for the above equation.

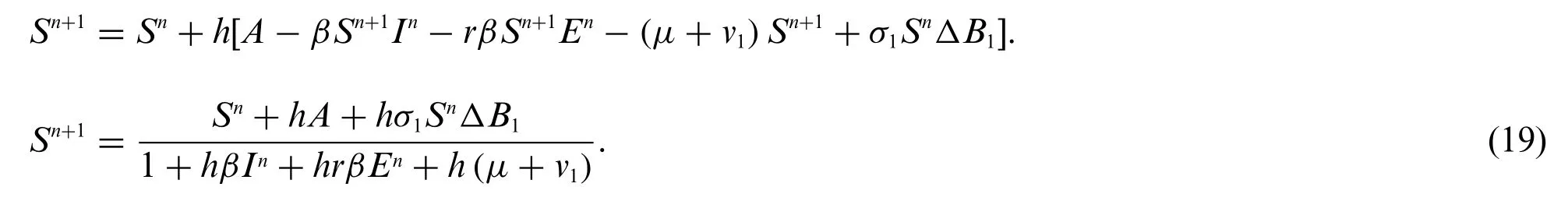
Similarly,we break the remaining system into a proposed method like(19),as follows:

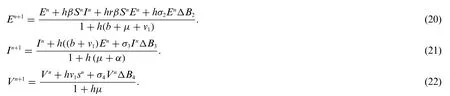
where,n=0,1,2,...,and discretization gap is denoted by“h”.

3.2 Stability Analysis

Theorem 5:The stochastic NSFD method is stable if the eigenvalues of Eqs.(19)-(22) lie in the unit circle for anyn≥0.

Proof:Let the functions L1, L2, L3, L4by assumingΔBn= 0, from the system ((19)-(22)) as follows:

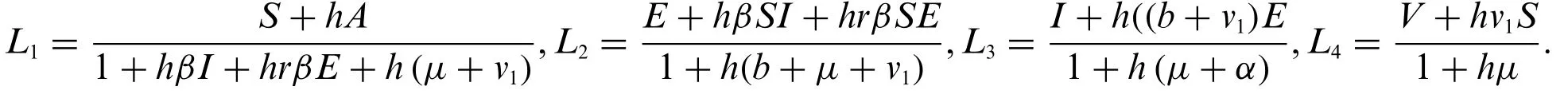
The elements of the Jacobean matrix are given as

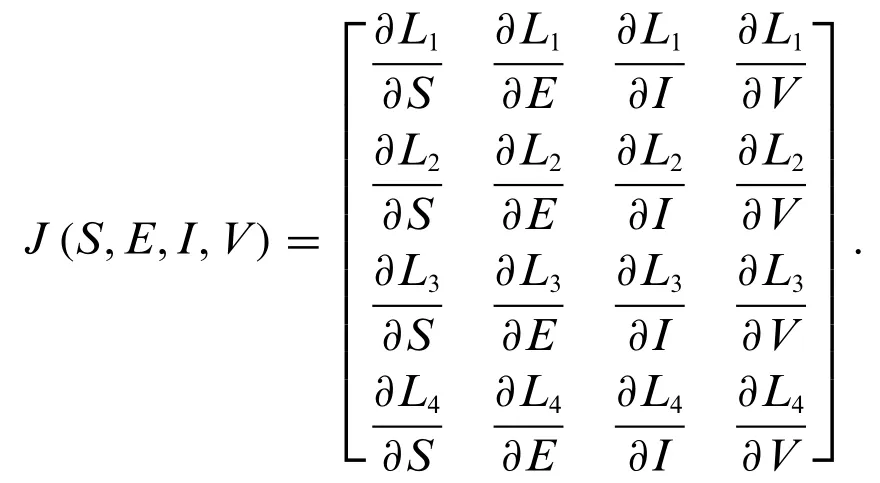
The given Jacobean matrix at K0=is as follows:

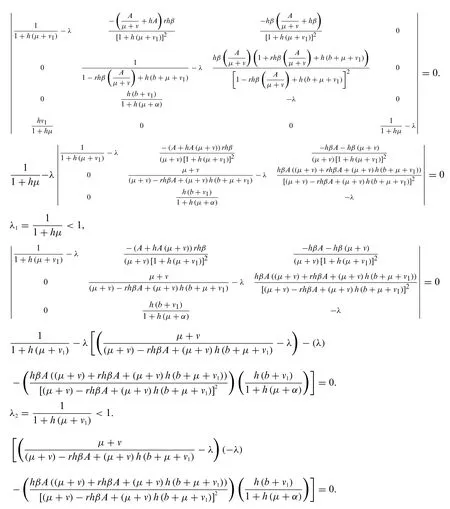
Hence,by using the Mathematica software all the eigen values of the above Jacobean matrix lie in the unit circle ifR0＜1.Thus,the system((19)-(22))is stable.

Now,for endemic equilibrium(EE)K1=(S*,E*,I*,V*).The given Jacobean matrix is

Using Mathematica software,the most many eigenvalues of the Jacobean is less than one whenR0＞1.Thus,endemic equilibrium is stable.

Figure 1: (Continued)

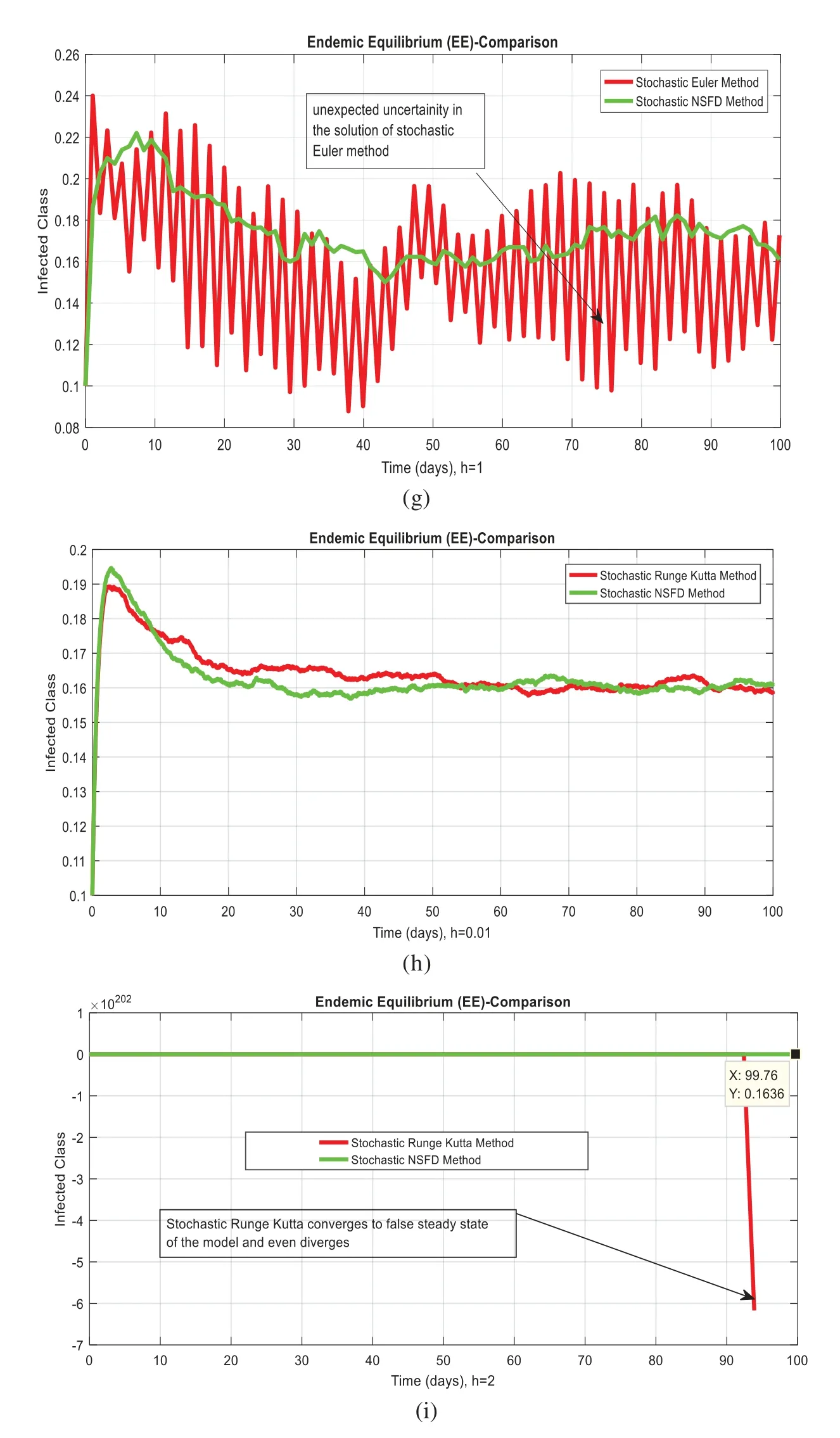
Figure 1: (a) Stochastic NSFD for DFE at h = 0.01 (b) Stochastic NSFD at h = 100 (c) stochastic NSFD for EE at h=100(d)Infected class(comparison)at h=0.01(e)Infected class(comparison)at h=0.7(f)Infected class(comparison)at h=0.01(g)Infected class(comparison)at h=1(h)Infected class(comparison-RK)of at h=0.01(i)Infected class(comparison-RK)at h=2

4 Results and Conclusion

Fig.1 admits the comparative analyses of the proposed approach with current methods in the sense of stochastic. The numerical experimentations can easily conclude that other stochastic numerical methods are conditionally convergent or diverge with larger time step values.The nature of biological properties is not consistent with existing literature methods.For this sake,the nonstandard finite difference is designed to restore the structure of continuous models.Computational methods like stochastic Euler, stochastic Runge Kutta, and Euler Maruyama are presented. Unfortunately, these methods are only applicable for the small step size.These methods diverge when we increase the time and do not obey the dynamical properties (positivity, stability, consistency, and boundedness). The stochastic nonstandard finite difference(SNSFD)method is appropriate for all complex and nonlinear stochastic epidemic models.The stochastic model is a reliable and efficient technique to handle highly nonlinear problems close to nature.The stochastic model is the extension of the deterministic model.We present the non-parametric perturbation technique for the said model. Our focus is to propose an always dynamically consistent, positive, and bounded scheme. That is why we investigate the nonstandard finite difference method in the sense of the stochastic.A comparison section is presented for the efficiency of the processes. Furthermore, we extend this idea to other types of models in the future,as shown in[27-31].

Acknowledgement:Thanks to all authors who contributed equally to preparing the article.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.