On the Mean Value of High-Powers of a Special Character Sum Modulo a Prime
Xiaodan Yuanand Wenpeng Zhang
School of Mathematics,Northwest University,Xi’an,China
ABSTRACT In this paper,we use the elementary methods,the properties of Dirichlet character sums and the classical Gauss sums to study the estimation of the mean value of high-powers for a special character sum modulo a prime,and derive an exact computational formula. It can be conveniently programmed by the “Mathematica” software, by which we can get the exact results easily.
KEYWORDS Quadratic character;the classical gauss sums;the mean value of high-power;computational formula
1 Introduction
Letpbe an odd prime,the quadratic character modulopis called the Legendre symbol,which is defined by

Many mathematicians have studied the properties of the Legendre symbol and obtained a series of important results(see[1-13]).Perhaps the most representative properties of the Legendre’s symbol are as follows:
Letpandqbe two distinct odd primes,then one has the quadratic reciprocal formula(see[14]:Theorem 9.8 or[15]:Theorems 4-6)
For any odd primepwithp≡1 mod 4,there exists two non-zero integersαpandβpsuch that(see[15]:Theorems 4-11)

In fact,the integersαpandβpin Eq.(1)can be represented by the Jacobsthal sumsφ2(r),which is(see[16]:Definition of the Jacobsthal sums)
wheresis any quadratic non-residue modulop.
Now we consider a sumA(r)be similar toβp. For any integersrwith(r,p)= 1 andk≥0, letA(r)andSk(p)be defined as follows:
In this paper,we give an exact computational formula forSk(p)withp≡1 mod 6,and prove the following result:
Theorem.Letpbe a prime withp≡1 mod 6,for any integerk,we have the identity
wheredandbare uniquely determined by 4p=d2+27b2,d≡1 mod 3 andb >0.
From this Theorem,we can immediately deduce the following four Corollaries:
Corollary 1.Letpbe a prime withp≡1 mod 6,then we have
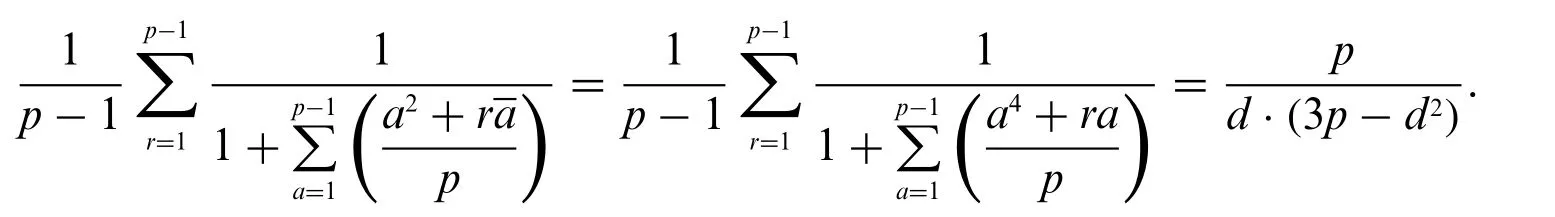
Corollary 2.Letpbe a prime withp≡1 mod 6,we have

Corollary 3.Letpbe a prime withp≡1 mod 6,then we have
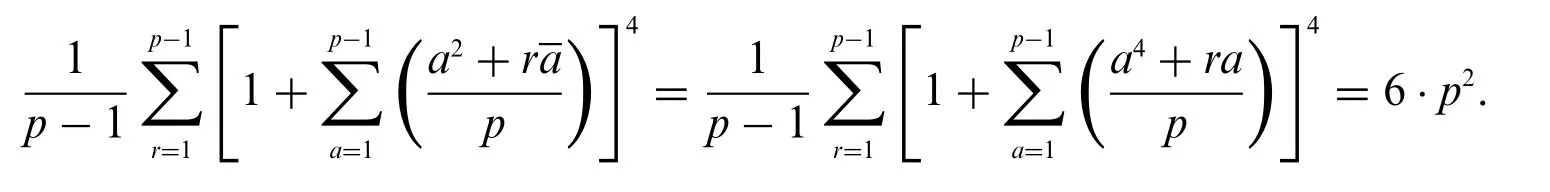
Corollary 4.Letpbe a prime withp≡1 mod 6,we have
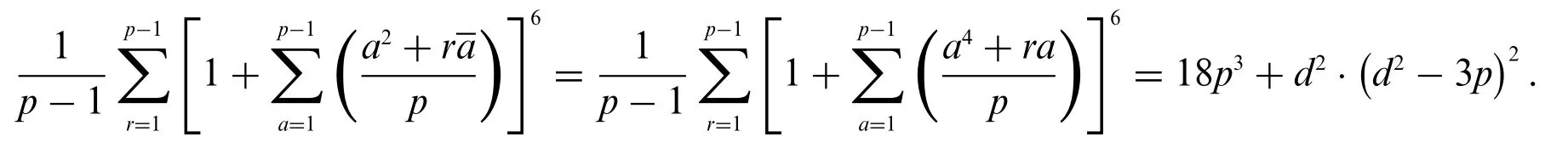
Some notes:In our Theorem,we only discuss the casep≡1 mod 6.Ifp≡5 mod 6,the result is trivial,see Proposition 6.1.2 in[16].In this case,for any integerrwith(r,p)=1,we have the identity
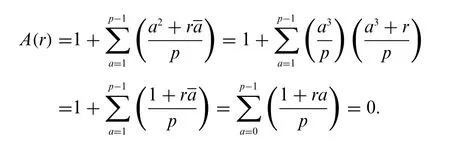
Thus,for all primepwithp≡5 mod 6 andk≥1,we haveSk(p)=0.
In addition,our Theorem holds for all negative integers.
Obviously, the advantage of our work is that it can transfer a complex mathematical computational problem into a simple form suitable for computer programming. It means that for any fixed primepwithp≡1 mod 6 and integerk,the exact value ofSk(p)can be calculated by our Theorem and a simple computer program.In Section 4,we give an example to calculate the exact results of the prime numberpwithin 200 satisfying conditionsp≡1 mod 6 andd≡1 mod 3.The exact results of calculation are summarised in Table 1.
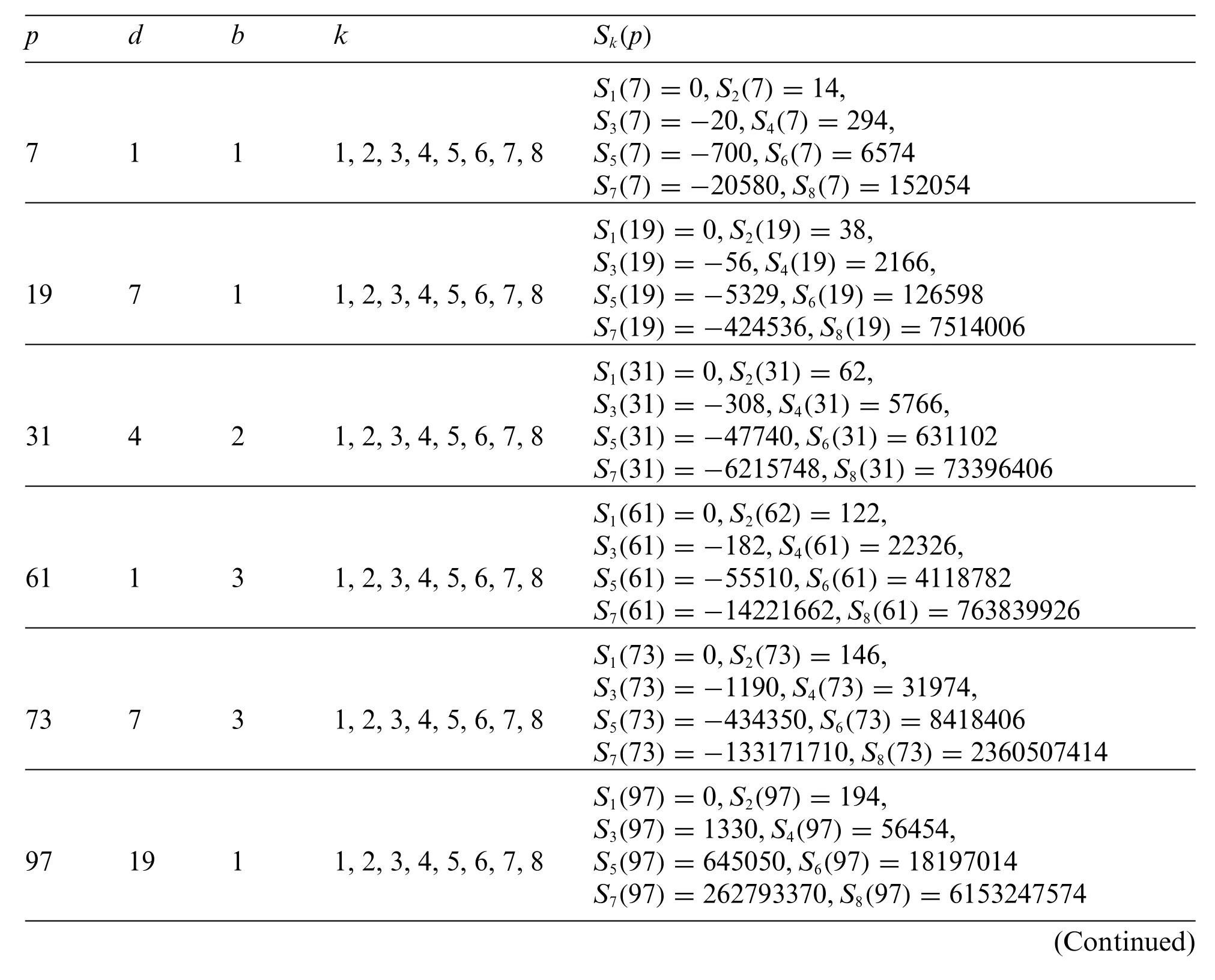
Table 1: The calculation of Sk(p)

Table 1 (continued)p d b k Sk(p)S1(103)=0,S2(103)=206,S3(103)=-1820,S4(103)=63654,103 13 3 1,2,3,4,5,6,7,8 S5(103)=-937300,S6(103)=22981486 S7(103)=-405475980,S8(103)=8087165174 S1(151)=0,S2(151)=302,S3(151)=-1748,S4(151)=136806,151 19 3 1,2,3,4,5,6,7,8 S5(151)=-1319740,S6(151)=65028622 S7(151)=-836979108,S8(151)=31764871286 S1(163)=0,S2(163)=326,S3(163)=3400,S4(163)=159414,163 25 1 1,2,3,4,5,6,7,8 S5(163)=2771000,S6(163)=89513446 S7(163)=1897026600,S8(163)=53193475094 S1(181)=0,S2(181)=362,S3(181)=-3458,S4(181)=196566,181 7 5 1,2,3,4,5,6,7,8 S5(181)=-3129490,S6(181)=118693102 S7(181)=-2379038298,S8(181)=75272130806
2 Several Lemmas
In this section,we give some simple Lemmas,which are necessary in the proofs of our Theorem.In addition,we need some properties of the classical Gauss sums and character sums,which can be found in many number theory books,such as [14,15] or [17], and we will not repeat them. First, we have the following:
Lemma 1.Letpbe a prime withp≡1 mod 3,for any third-order characterλmodulop,we have the identity
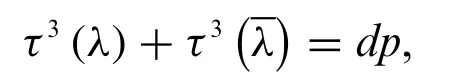
wheredenotes the classical Gauss sums withe(y)=e2πiyandi2= -1,dis the same as the one in the Theorem.
Proof.See references[18]or[19].
Lemma 2.Letpbe an odd prime,for any non-principal characterχmodulop,we have the identity
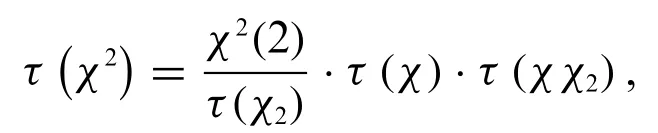
wheredenotes the Legendre’s symbol modulop.
Proof.From the properties of the classical Gauss sums we have

On the other hand,for any integerbwith(b,p)=1,from the identity
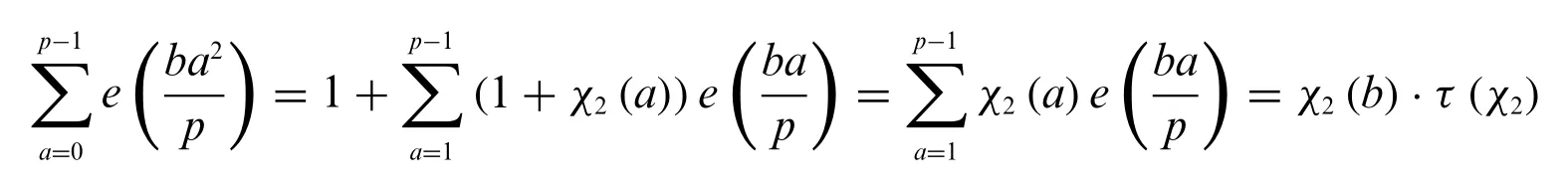
we also have
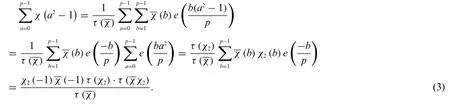
From Eqs.(2)and(3)we have the identity
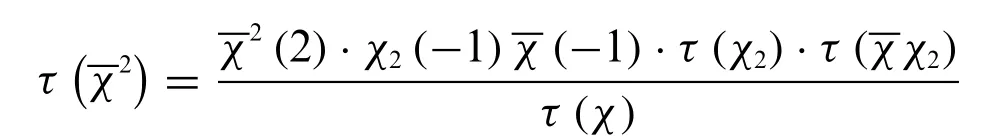
or

This proves Lemma 2.
Lemma 3.Letpbe a primepwithp≡1 mod 6,then for any integerrwith(r,p)= 1 and three order characterλmodulop,we have the identity
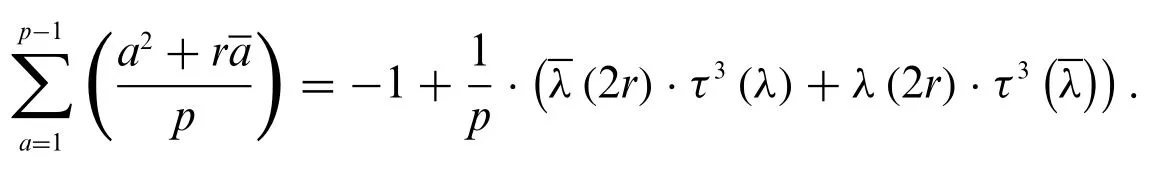
Proof.From the characteristic function of the cubic residue modulop,we have

Applying Eq.(4)we have
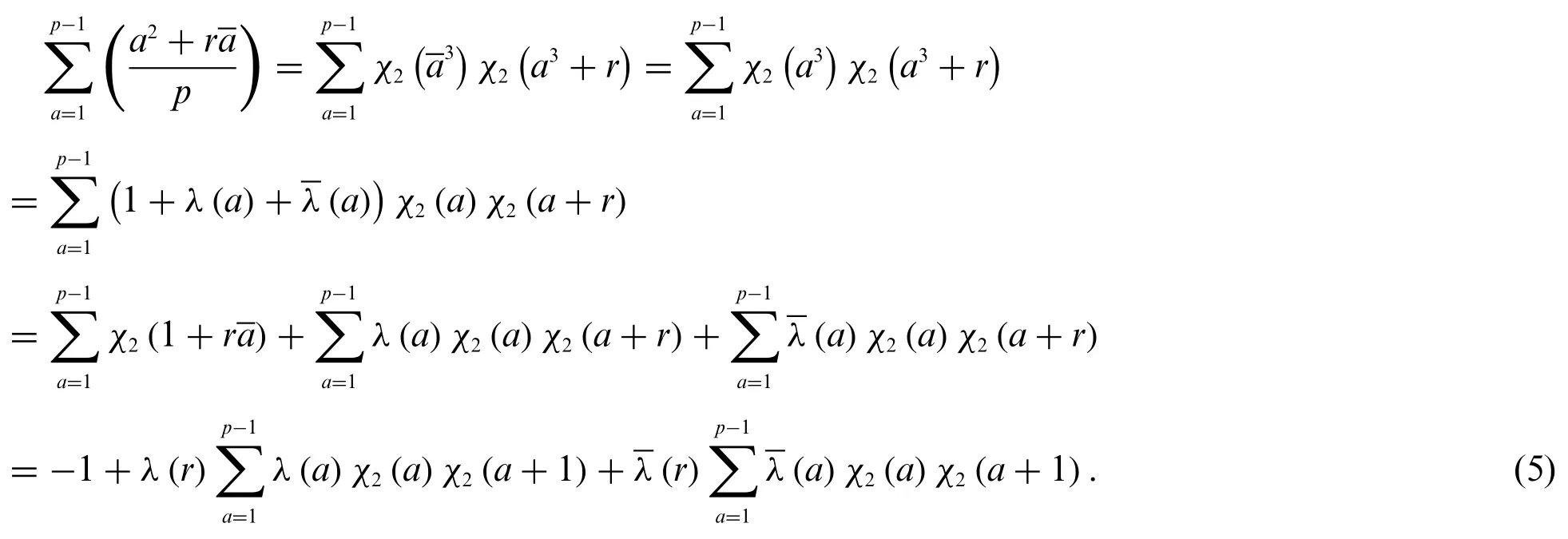
From the properties of the classical Gauss sums,we have
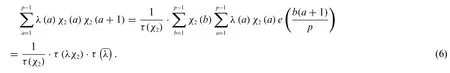
Takingχ=λin Lemma 2,we have

Note thatτ(λ)·=p,from Eqs.(6)and(7)we have

Similarly,we also have

Combining Eqs.(5),(8)and(9)we can deduce that

This proves Lemma 3.
Lemma 4.Letpbe any odd prime withp≡1 mod 6, then for any integersk≥3 andrwith(r,p)=1,we have the third order recursive formula

wheredis the same as defined in the Theorem.
Proof.Note thatλ3==χ0,the principal character modulop,from Lemma 1 and Lemma 3 we have

Indeed,for any integerk≥3,from Eq.(10)we have the third order recursive formula
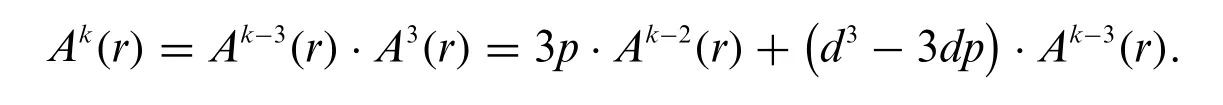
This proves Lemma 4.
Lemma 5.Letpbe any odd prime withp≡1 mod 6,then we have
S0(p)=1,S1(p)=0,S2(p)=2p,S3(p)=d·(d2-3p)and
Sk(p)=3p·Sk-2(p)+(d3-3pd)·Sk-3(p)for allk≥4.
Proof.From the definition
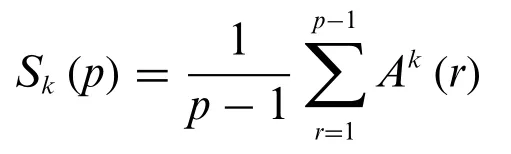
and the orthogonality of characters modulop,we have

From Eq.(10)we also have
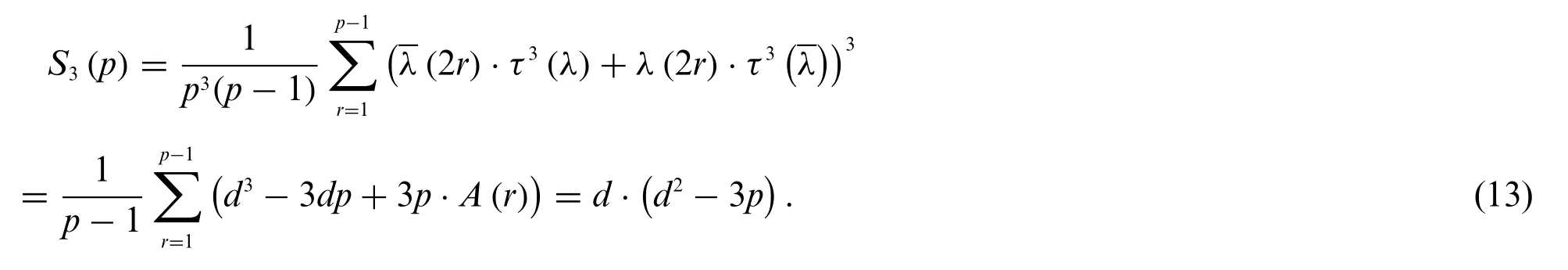
Ifk≥4,then from Lemma 4 we have

Now Lemma 5 follows from Eqs.(11)-(14).
3 Proof of the Theorem
In this section,we complete the proof of our Theorem.It is clear that the characteristic equation of the third order linear recursive formula

is

Note that 4p=d2+27b2,from Eq.(16)we have
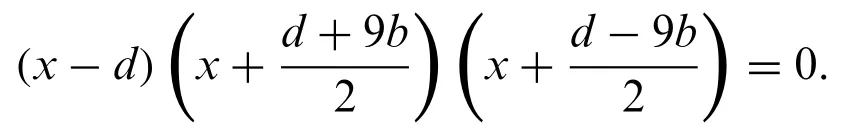
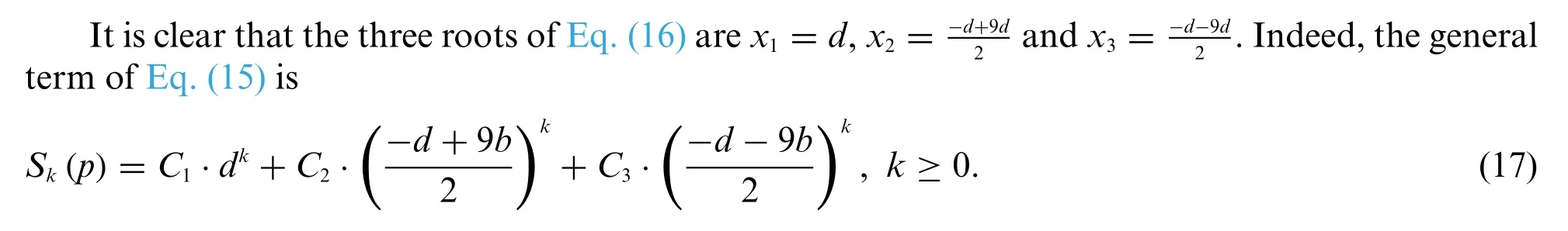
From Lemma 5 we have

Solving the Eq.(18)we can getFrom Eq.(17)we have
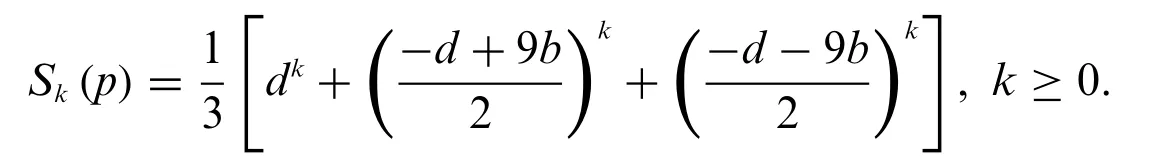
This proves our Theorem.
Obviously,using Lemma 4 we can also extendkin Lemma 5 to all negative integers,which leads to the Corollary 1 and the Corollary 2.
This completes the proofs of our all results.
4 Conclusion
In this paper,we give an exact computational formula forSk(p)withp≡1 mod 6,which is,for any integerk,we have the identity

wheredandbare uniquely determined by 4p=d2+27b2,p≡1 mod 6 andb >0.
Meanwhile, the problems of calculating the mean value of high-powers of quadratic character sums modulo a prime are given.
In the end,we use the mathematical software“Mathematica”to program and calculate the exact values ofS1(p)toS8(p)of the prime numberpwithin 200 satisfying conditionsp≡1 mod 6 andd≡1 mod 3, as shown in Table 1. Its application can also extend toSk(p)that satisfies conditionsp≡1 mod 6 andd≡1 mod 3(where 4p=d2+27b2)for anyk.See the Appendix A for this specific computer program.
Acknowledgement:The authors would like to thank the editor and referees for their suggestions and critical comments that substantially improve the presentation of this work.
Funding Statement:This work was supported by the N.S.F.(12126357)of China.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
Appendix A.

 Computer Modeling In Engineering&Sciences2023年7期
Computer Modeling In Engineering&Sciences2023年7期
- Computer Modeling In Engineering&Sciences的其它文章
- Edge Intelligence with Distributed Processing of DNNs:A Survey
- Turbulent Kinetic Energy of Flow during Inhale and Exhale to Characterize the Severity of Obstructive Sleep Apnea Patient
- The Effects of the Particle Size Ratio on the Behaviors of Binary Granular Materials
- A Novel Light Weight CNN Framework Integrated with Marine Predator Optimization for the Assessment of Tear Film-Lipid Layer Patterns
- Implementation of Rapid Code Transformation Process Using Deep Learning Approaches
- A New Hybrid Hierarchical Parallel Algorithm to Enhance the Performance of Large-Scale Structural Analysis Based on Heterogeneous Multicore Clusters
