Minimal Doubly Resolving Sets of Certain Families of Toeplitz Graph

Muhammad Ahmad,Fahd Jarad, Zohaib Zahid and Imran Siddique

1Department of Mathematics,University of Management and Technology,Lahore,54770,Pakistan

2Department of Mathematics,Cankaya University,Etimesgut,Ankara,06790,Turkey

3Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,40402,Taiwan

ABSTRACTThe doubly resolving sets are a natural tool to identify where diffusion occurs in a complicated network.Many realworld phenomena,such as rumour spreading on social networks,the spread of infectious diseases,and the spread of the virus on the internet,may be modelled using information diffusion in networks.It is obviously impractical to monitor every node due to cost and overhead limits because there are too many nodes in the network,some of which may be unable or unwilling to send information about their state.As a result, the source localization problem is to find the number of nodes in the network that best explains the observed diffusion.This problem can be successfully solved by using its relationship with the well-studied related minimal doubly resolving set problem,which minimizes the number of observers required for accurate detection.This paper aims to investigate the minimal doubly resolving set for certain families of Toeplitz graph Tn(1,t),for t ≥2 and n ≥t+2.We come to the conclusion that for Tn(1,2),the metric and double metric dimensions are equal and for Tn(1,4),the double metric dimension is exactly one more than the metric dimension.Also,the double metric dimension for Tn(1,3)is equal to the metric dimension for n=5,6,7 and one greater than the metric dimension for n ≥8.

KEYWORDS Family of Toeplitz graph;resolving sets;metric dimension;doubly resolving sets;double metric dimension

1 Introduction and Preliminaries

To understand the abstract structure of graphs,graph invariants can be a powerful tool.Metric generators in graphs have evolved into a variety of distinct types based on their popularity or usefulness.As an example,virus propagation in complicated network difficulties can be detected using the double metric dimension(DMD).

We consider a finite,undirected,and connected graphΓwith the edge setEΓand the vertex setVΓ.In a connected graphΓ, the distance between a pair of distinct vertices, saykandlinΓ, is the smallest path length among the lengths of all paths between them and is represented byd(k,l).For any two distinct verticesjandkinVΓ, a vertexl∈VΓresolves the verticesjandkif the conditiond(j,l)/=d(k,l)holds true.Letkbe a vertex ofΓandHΓ= {hμ|1 ≤μ≤ρ} be an ordered subset of the vertex setVΓ,thenr(k,HΓ)is the representation ofkwith respect toHΓwhich is theρ-vectoralso known as vector of metric coordinates.If each vertex of graphΓpossesses a unique vector of metric coordinates with respect toHΓthen the subsetHΓis called a resolving set for graphΓ.If the subsetHΓis the resolving set with the minimum number of elements inΓ,then its count becomes the metric dimension(MD)ofΓand can be denoted as dim(Γ).

It is common in computer science,chemistry,biology,and operations research to structure graph theory models.In graph theory,the computation of the resolving sets and MD for general graphs is complex.In various disciplines,such as optimization,pattern recognition,and loran detecting devices,the MD has gained all the interest due to its applications.

Slater[1],a mathematician,was the first to discover the term MD.This notion was used to describe the study of the Loran or sonar model station.Another mathematician, Harary, independently described the concept of MD with the help of Harary et al.[2].Additionally,this concept cleared the path for finding the unique recipient of a message on a network.Since then,several studies have been done on resolving sets,including[3,4].Many different tasks can be accomplished with resolving sets,like network discovery and verification[5],strategies for the mastermind games[6],as well as digital geometry,pattern recognition,and processing of images[7].The minimum order of a resolving set of Hamming graphs closely relates to the problem of weighing the coins discussed in[8,9].Also,there are numerous applications in different fields,such as chemical structures[10],robotics[11],combinatorial optimization[12],geographic routing protocols[13]for the theoretical study of the MD.

The MD of any graph is a computationally difficult problem to solve.So, valuable bounds for different types of graphs have been found.The MD of all connected graphs, as well as the MD of certain well-known graph families,such as trees,pathways,and complete graphs,were established by Chartrand et al.[10,14].For some families of generalized Petersen graphs,MD bounds were studied in [15].The MD for chorded cycles and kayak paddles graphs was found to be constant by Ahmad et al.[16].Many authors have extensively studied the MD of path-related graphs.The MD of the Kenser graph was computed by Hui et al.[17].On the other hand,Alholi et al.[18]also contributed to this area by finding that the MD is constant.Buczkowski and others[19]presented a generic concept ofk-dimensional graphs.The NP-completeness of the MD for general graphs was demonstrated by Khuller et al.[11].The minimum order of a resolving set of Jahangir graphs has also been discussed in detail by Tomescu et al.[20].

Caceres et al.[21]developed the concept of doubly resolving sets(DRSs)of a graphΓ,demonstrating that the MD of the Cartesian productΓ□Γis closely linked to the minimal doubly resolving sets(MDRSs)ofΓ.Consider the verticesk1,k2,l1,l2∈VΓ,then any pair of verticesk1,k2is said to be doubly resolved by the verticesl1,l2if the conditiond(k1,l1)-d(k1,l2)/=d(k2,l1)-d(k2,l2),holds true.A subsetNΓ∈VΓis said to be a DRS,if any two distinct vertices of graphΓare doubly resolved by some two vertices of the subsetNΓ.A MDRS is a DRS having minimum order.The order of MDRS is denoted byψ(Γ)and is termed the DMD ofΓ.Note that if the verticesl1,l2doubly resolve the verticesk1,k2thend(k1,l1)-d(k2,l1)/= 0 ord(k1,l2)-d(k2,l2)/= 0.For all graphsΓ, any DRS is obviously a resolving set,with dim(Γ)≤ψ(Γ).The MDRS problem has been proven to be NP-hard in the context of general graphs[22].Furthermore,it was shown in[21]that the upper bound on the MD of the Cartesian product ofΓandΩcan be stated as;dim(Γ□Ω)≤dim(Γ)+ψ(Ω)-1.

Therefore,DRSs are essential for studying the MD of Cartesian product graphs.These results have inspired us to work on finding the MDRSs.Also, MDRSs themselves have a unique combinatorial nature that can be seen in their integer programming model,which was shown in[22].There are several families of graphs for which the problem of finding the MDRS has been examined.For example,MDRSs of prisms [23], convex polytopes [24], and Hamming graphs [25] have all been studied in the literature.The family of circulant graphs in [26] was found to have the same MD and MDRS.The MDRSs for the line graphs of prisms and sunlet graphs were found in [27].For the first time,Chen et al.explicitly approximated the upper and lower bounds for the MDRS problem[28].In[29],the minimal resolving sets and DMD of the line graph of chorded cycles were examined.Authors demonstrated that the DMD ofL(Cnt)is exactly one greater than its MD.Ahmad et al.discussed the problem of finding the minimal resolving set and MDRS for line graphs of kayak paddles graphs[30].The authors in[31,32]presented some families of convex polytopes with constant DMD.While solving the MDRS problem,certain families of Harary graphs,layer-sun graphs have also been investigated in [33,34], respectively.Cocktail, jellyfish and necklace graphs and their line graphs have also been studied for the MD and MDRS problems,see[35-37].

Our research is the continuation of the literature work mentioned earlier.We have investigated the DMD for some particular classes of Toeplitz graphs to contribute to our knowledge of this distancebased parameter in graphs.However,this variant is helpful in many fields,for instance,diffusion over the network, epidemics in human beings, the origin of a disease outbreak, etc.Using MDRSs, it is possible to identify the source of diffusion in complicated networks.Attempting to find the source of an infection in an extensive network might be difficult,but it is still an exciting challenge.For example,to detect the spread of the virus throughout a network,we need to know when specific nodes in the network are infected.However,maintaining observer nodes that can report their infection time may be costly.In addition,the position of a node in the network affects how much information it contains.Which nodes should we use as observers in order to increase our chances of correctly identifying the source? Because of its close relationship to another well-known DRS problem, we can reduce the number of observers required to achieve perfect detection even if the initial time at which an epidemic spreads is unknown[38,39].

Liu et al.[40]determined the MD of some families of Toeplitz graphTn(1,t)forn≥t+2 given in the following theorems:

Theorem 1.1.Forn≥4,the metric dimension of Toeplitz graphTn(1,2)=2.

Theorem 1.2.Forn≥6,the metric dimension of Toeplitz graphTn(1,4)=2.

Theorem 1.3.Forn≥5,the metric dimension of Toeplitz graphTn(1,3)=3.

Detailed discussion of the rest of the article is provided in the following sections:

• Our discussion of Toeplitz graphs in Section 2 included the computation of MDRSs for the family of Toeplitz graphsTn(1,2)forn≥4.

• The MDRSs for the family of Toeplitz graphsTn(1,4),forn≥6 were conjectured in Section 3.

• The MDRSs for the family of Toeplitz graphTn(1,3)forn≥5,were discussed in Section 4.

• In Section 5,we conclude this article by expressing an opinion.

2 Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,2)

For a graphΓwithnvertices labelled as{1,2,...,n}its adjacency matrixAisn×nmatrix whosejkthentry is 1 if the vertexjand vertexkjoined by an edge and 0 otherwise.Ann×nmatrixB=bjkis known as Toeplitz matrix ifbjk=bj+1,k+1for each{j,k=1,...,n-1}.A simple undirected graphTnis Toeplitz graph if matrixn×nwhich isB=bjkis the symmetric Toeplitz matrix and for allj,k={1,...,n}satisfied the following:edgej,kis inEΓiffbjk=bkj=1.Ann×nmatrixBwill be labelled 0,1,...,n-1 which hasndistinct diagonals.The main diagonal hasbjj= 0 for allj=1,...,n,so Toeplitz graph has no loop.The diagonals{x1,x2,...,xq}containing ones 0＜x1＜x2＜...＜xq ＜n.The Toeplitz graphTn ＜x1,x2,...,xq ＞with vertex set{1,2,...,n}has edgej,kfor 1 ≤j≤k≤n,occurs iffk-j=xpfor somep,1 ≤p≤q.Toeplitz graphs are defined as graphs formed from Toeplitz matrices.Specifically,in this part,we computed the MDRSs for the family of Toeplitz graphTn(1,2).Fig.1 illustrates the graphT11(1,2).

Figure 1:The Toeplitz graph T11(1,2)

It follows from Theorem 1.1 thatforn≥4.We will also calculate thatforn≥4.To compute the distances between the vertices of the Toeplitz graphTn(1,2):DefineSω(e0)={e∈Tn(1,2):d(e0,e)=ω},which is the vertex subset inVTn(1,2)at distanceωfrome0.The Table 1 shows the setsSω(e0)for Toeplitz graphTn(1,2),wheren≥4.

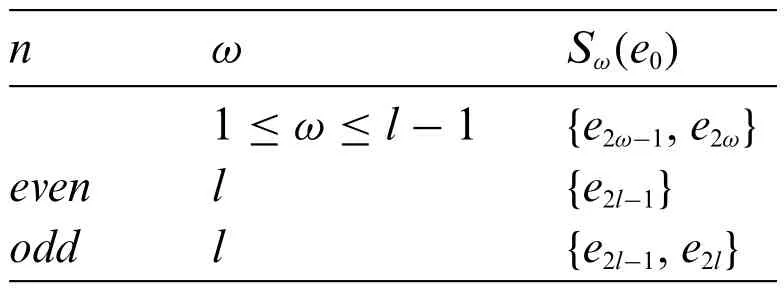
Table 1: Sω(e0)for Tn(1,2)

Due to the symmetry ofTn(1,2),wheren≥4:d(eω,eν)=d(e0,e|ν-ω|)if 0 ≤|ν-ω|≤n-1.

Due to the fact that,in order to calculate the distance between any pair of vertices inVTn(1,2),we must know the distanced(e0,e)for eache∈Tn(1,2).

Lemma 2.1.LetTn(1,2)be the family of Toeplitz graph, thenfor any even positive integern≥4.

Proof.Consider the casen=2l,wherel≥2.We must prove thatfor any even positive integern≥4.So, finding a DRS of order 2 is sufficient.The Table 2 displays the metric coordinate vectors for all vertices ofTn(1,2)with respect to the setNTn(1,2)={e1,en-1}.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 2 is 1.Using Table 2, we may check that there exist a pair of verticesf1,f2∈Sω(e0), for someω∈{1,2,...,l}, such as the conditionr(f1,NTn(1,2))-r(f2,NTn(1,2))/= 0, holds true.Also, there exist the verticesf1∈Sω(e0)andf2∈Sν(e0)for anyω,ν∈{1,2,...,l}, such asω/=ν, then the conditionr(f1,NTn(1,2))-r(f2,NTn(1,2))/=ω-ν,holds true.Therefore,the setNTn(1,2)={e1,en-1}is the MDRS.As a result,the Lemma 2.1 holds.

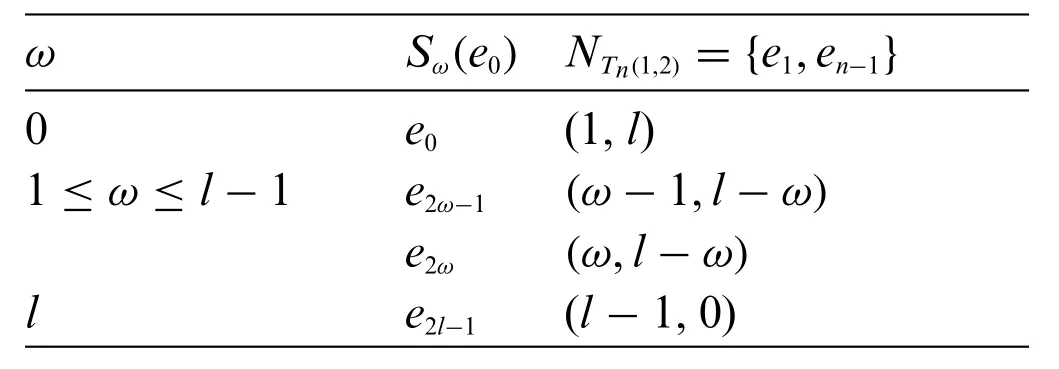
Table 2: The metric coordinate vectors for Tn(1,2),for any even positive integer n ≥4

Lemma 2.2.LetTn(1,2)be the family of Toeplitz graph,thenfor any odd positive integern≥5.

Proof.Consider the casen=2l+1,wherel≥2.We must prove thatfor any odd positive integern≥5.So,finding a DRS of order 2 is sufficient.The Table 3 displays the metric coordinate vectors for all vertices ofTn(1,2)with respect to the setNTn(1,2)={e0,en-1}.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 3 is 0.Using Table 3, we may check that there exist a pair of verticesf1,f2∈Sω(e0), for someω∈{1,2,...,l}, such as the conditionr(f1,NTn(1,2))-r(f2,NTn(1,2))/= 0, holds true.Also, there exist the verticesf1∈Sω(e0)andf2∈Sν(e0)for anyω,ν∈{1,2,...,l}, such asω/=ν, then the conditionr(f1,NTn(1,2))-r(f2,NTn(1,2))/=ω-ν,holds true.Therefore,the setNTn(1,2)={e0,en-1}is the MDRS.As a result,the Lemma 2.2 holds.

The main theorem is stated below by using Lemmas 2.1 and 2.2.

Table 3: The metric coordinate vectors for Tn(1,2),for any odd positive integer n ≥5

Theorem 2.1.LetTn(1,2)be the family of Toeplitz graph.Thenforn≥4.

Example 2.1.For the Toeplitz graphTn(1,2),wheren≥4,let us consider the setNT8(1,2)={e1,e7}.Now, the vectors of metric coordinates forT8(1,2)with respect to the setNT8(1,2)are:r(e0|NT8(1,2))=(1,4),r(e1|NT8(1,2))=(0,3),r(e2|NT8(1,2))=(1,3),r(e3|NT8(1,2))=(1,2),r(e4|NT8(1,2))=(2,2),r(e5|NT8(1,2))=(2,1),r(e6|NT8(1,2))=(3,1),r(e7|NT8(1,2))=(3,0).Thus,the setNT8(1,2)is clearly a DRS,as can be observed.

3 Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,4)

Specifically,in this part,we computed the MDRSs for the family of Toeplitz graphTn(1,4).Fig.2 illustrates the graphT11(1,4).

Figure 2:The Toeplitz graph T11(1,4)

It follows from Theorem 1.2 thatforn≥6.We will also calculate thatforn≥6.To compute the distances between the vertices of the Toeplitz graphTn(1,4):DefineSω(e0)={e∈Tn(1,4):d(e0,e)=ω},which is the vertex subset inVTn(1,4)at distanceωfrome0.The Table 4 shows the setsSω(e0)for Toeplitz graphTn(1,4),wheren≥6.

Table 4: Sω(e0)for Tn(1,4)

Due to the symmetry ofTn(1,4),wheren≥6:d(eω,eν)=d(e0,e|ν-ω|)if 0 ≤|ν-ω|≤n-1.Due to the fact that,in order to calculate the distance between any pair of vertices inVTn(1,4),we must know the distanced(e0,e)for eache∈Tn(1,4).

Lemma 3.1.for alln≥6.

Proof.We already know thatforn≥6.As a result,it suffices to demonstrate that no subsetNTn(1,4)⊆VTn(1,4)of order 2 is a DRS forTn(1,4).We can assume thate0∈NTn(1,4)because of the symmetry ofTn(1,4).Table 5 lists the non-doubly resolved pair of vertices fromVTn(1,4)that correspond to each of the five distinct forms of setNTn(1,4).Let us explain why the verticesen-2,en-3cannot be doubly resolved by any two vertices of the setNTn(1,4)= {e0,eω;ω=n-1}.It is clear that forω=n- 1, we haved(e0,en-2)=d(e0,e|n-2|)=l,d(e0,en-3)=d(e0,e|n-3|)=l+ 1,d(eω,en-2)=d(e0,e|n-2-ω|)= 1 andd(eω,en-3)=d(e0,e|n-3-ω|)= 2.So,d(e0,en-2)-d(e0,en-3)=d(eω,en-2)-d(eω,en-3)= -1, that is, the setNTn(1,4)= {e0,eω;ω=n-1} is not a DRS ofTn(1,4).The non-doubly resolved pairs of vertices for all the other types of setNTn(1,4)listed in Table 5 can be verified in the same way.

Table 5: Non-doubly resolved pairs for Tn(1,4),where n ≥6

Lemma 3.2.Letn≡0(mod4)andn≥8,we have

Proof.Suppose thatn≡0(mod4) andn≥8.We need to prove thatforn≥8.So, finding a DRS having order 3 is sufficient.Now, from Table 4 using the setsSω(e0), the following Table 6 illustrates the metric coordinate vectors for all vertices ofTn(1,4)with respect to the setNTn(1,4)={e0,e2,en-3},wheren=4landl≥2 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 6 is 0.Using Table 6, we may check that there exist a pair of verticesg1,g2∈Sω(e0), for someω∈{1,2,...,l+1},such as the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=0,holds true.Also,there exist the verticesg1∈Sω(e0)andg2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=ω-ν,holds true.Therefore,the setNTn(1,4)={e0,e2,en-3}is the MDRS.As a result,the Lemma 3.2 holds.

Table 6: The metric coordinate vectors for Tn(1,4),where n=4l,l ≥2

Lemma 3.3.Letn≡1(mod4)andn≥9,we have

Proof.Suppose thatn≡1(mod4)andn≥9.We need to prove thatforn≥9.So,finding a DRS having order 3 is sufficient.Now,from Table 4 using the setsSω(e0),the following Table 7 illustrates the metric coordinate vectors for all vertices ofTn(1,4)in relation to the setNTn(1,4)={e0,e2,en-3},wheren=4l+1 andl≥2 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 7 is 0.Using Table 7, we may check that there exist a pair of verticesg1,g2∈Sω(e0), for someω∈{1,2,...,l+1},such as the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=0,holds true.Also,there exist the verticesg1∈Sω(e0)andg2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=ω-ν,holds true.Therefore,the setNΓ={e0,e2,en-3}is the MDRS.As a result,the Lemma 3.3 holds.

Table 7: The metric coordinate vectors for Tn(1,4),where n=4l+1,l ≥2

Lemma 3.4.Letn≡2(mod4)andn≥6,we have

Proof.Suppose thatn≡2(mod4) andn≥6.We need to prove thatforn≥6.So, finding a DRS having order 3 is sufficient.Now, from Table 4 using the setsSω(e0), the following Table 8 illustrates the metric coordinate vectors for all vertices ofTn(1,4)with respect to the setNTn(1,4)={e0,e2,en-3},wheren=4l+2 andl≥1 be an integer.

Table 8: The metric coordinate vectors for Tn(1,4),where n=4l+2,l ≥1

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 8 is 0.Using Table 8, we may check that there exist a pair of verticesg1,g2∈Sω(e0), for someω∈{1,2,...,l+1},such as the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=0,holds true.Also,there exist the verticesg1∈Sω(e0)andg2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=ω-ν,holds true.Therefore,the setNTn(1,4)={e0,e2,en-3}is the MDRS.As a result,the Lemma 3.4 holds.

Lemma 3.5.Letn≡3(mod4)andn≥7,we have

Proof.Suppose thatn≡3(mod4) andn≥7.We need to prove thatforn≥7.So, finding a DRS having order 3 is sufficient.Now, from Table 4 using the setsSω(e0), the following Table 9 illustrates the metric coordinate vectors for all vertices ofTn(1,4)with respect to the setNTn(1,4)={e0,e2,en-3},wheren=4l+3 andl≥1 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 9 is 0.From Table 9, we may check that there exist a pair of verticesg1,g2∈Sω(e0), for someω∈{1,2,...,l+2},such as the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=0,holds true.Also,there exist the verticesg1∈Sω(e0)andg2∈Sν(e0)for anyω,ν∈{1,2,...,l+2}such asω/=ν,then the conditionr(g1,NTn(1,4))-r(g2,NTn(1,4))/=ω-ν,holds true.Therefore,the setNTn(1,4)={e0,e2,en-3}is the MDRS.As a result,the Lemma 3.5 holds.

The main theorem is stated below by using Lemmas 3.2-3.5.

Table 9: The metric coordinate vectors for Tn(1,4),where n=4l+3,l ≥1

Theorem 3.1.LetTn(1,4)be the family of Toeplitz graph.Thenforn≥6.

4 Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,3)

Specifically,in this part,we computed the MDRSs for the family of Toeplitz graphTn(1,3).Fig.3 illustrates the graphT11(1,3).

Figure 3:The Toeplitz graph T11(1,3)

It follows from Theorem 1.3 thatforn≥5.We will also calculate that

To compute the distances between the vertices of the Toeplitz graphTn(1,3):DefineSω(e0)={e∈Tn(1,3):d(e0,e)=ω},which is the vertex subset inVTn(1,3)at distanceωfrome0.The Table 10 shows the setsSω(e0)for Toeplitz graphTn(1,3),wheren≥5.

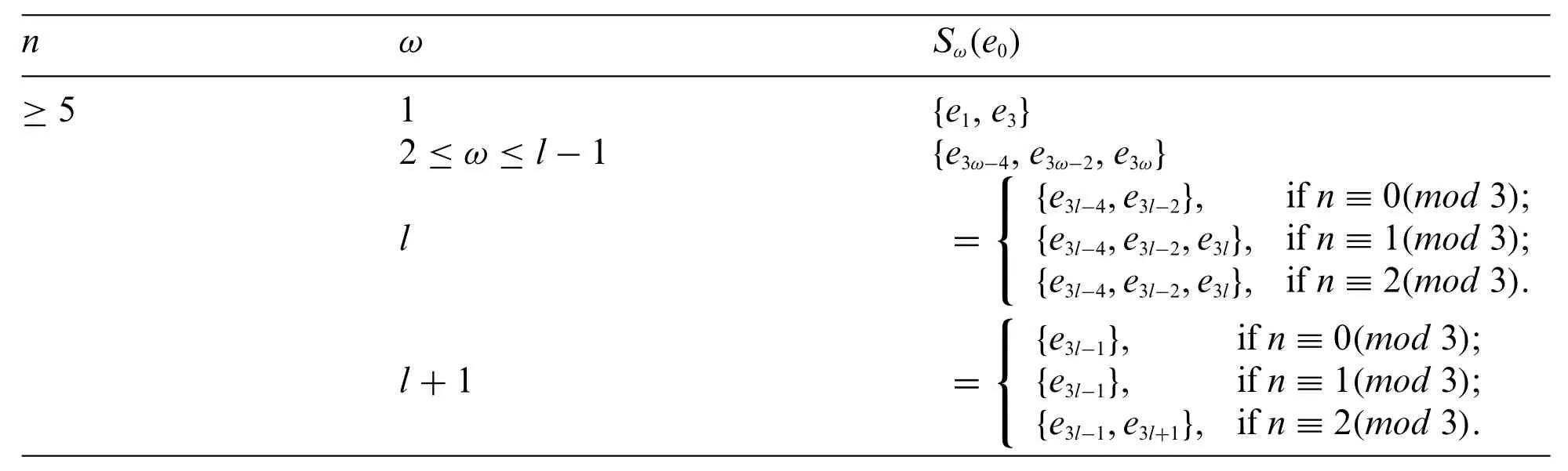
Table 10: Sω(e0)for Tn(1,3)

Due to the symmetry ofTn(1,3),wheren≥5:d(eω,eν)=d(e0,e|ν-ω|)if 0 ≤|ν-ω|≤n-1.Due to the fact that,in order to calculate the distance between any pair of vertices inVTn(1,3),we must know the distanced(e0,e)for eache∈Tn(1,3).

Lemma 4.1.,for alln≥5.

Proof.We already know that,forn≥5.As a result,it suffices to demonstrate that no subsetNTn(1,3)⊆VTn(1,3)of order 3 is a DRS forTn(1,3).We can assume thate0∈NTn(1,3)because of the symmetry ofTn(1,3).Table 11 lists the non-doubly resolved pair of vertices fromVTn(1,3)that correspond to each of the seven distinct forms of setNTn(1,3).Let us explain why the verticesen-2,en-1cannot be doubly resolved by any two vertices of the setNTn(1,3)= {e0,eω,eν;ω= 1,ν=n-2}.It is clear that forω= 1,ν=n-2,we haved(e0,en-2)=d(e0,e|n-2|)=l,d(e0,en-1)=d(e0,e|n-1|)=l+1,d(eω,en-2)=d(e0,e|n-2-ω|)=l-1,d(eω,en-1)=d(e0,e|n-1-ω|)=l,d(eν,en-2)=d(e0,e|n-2-ν|)= 0 andd(eν,en-1)=d(e0,e|n-1-ν|)= 1.So,d(e0,en-2)-d(e0,en-1)=d(eω,en-2)-d(eω,en-1)=d(eν,en-2)-d(eν,en-1)=-1,that is,the setNTn(1,3)={e0,eω,eν;ω=1,ν=n-2}is not a DRS ofTn(1,3).The nondoubly resolved pairs of vertices for all the other types of setNTn(1,3)listed in Table 11 can be verified in the same way.

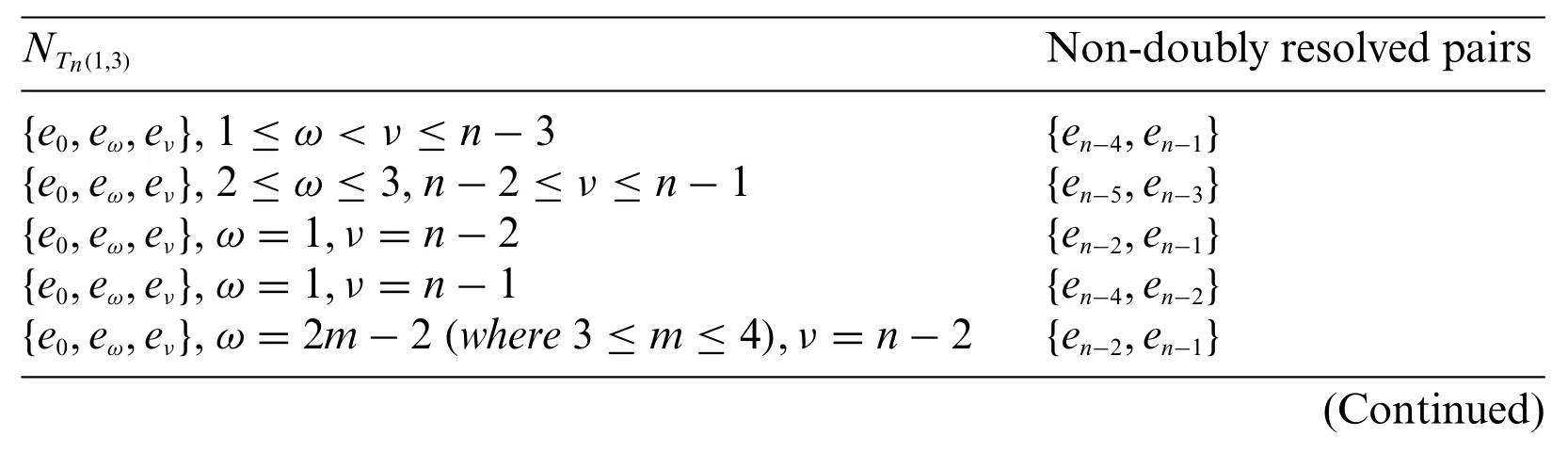
Table 11: Non-doubly resolved pairs for Tn(1,3),where n ≥5

Table 11 (continued)

Lemma 4.2.Letn≡0(mod3)forn≥6,we have

Proof.Suppose thatn≡0(mod3)andn≥6.Then,in the casen≡0(mod3)andn=6,the MDRS forT6(1,3)isNTn(1,3)= {e0,e1,e2}.Now, for the casen≡0(mod3) andn ＞6, we need to prove thatfinding a DRS having order 4 is sufficient.From Table 10 using the setsSω(e0),the following Table 12 illustrates the metric coordinate vectors for all vertices ofTn(1,3)with respect to the setNTn(1,3)={e0,e1,e2,en-2},wheren=3l,andl≥3 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 12 is 0.Using Table 12, we may check that there exist a pair of verticesh1,h2∈Sω(e0)for someω∈{1,2,...,l+1}such as the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=0,holds true.Also,there exist the verticesh1∈Sω(e0)andh2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=ω-ν,holds true.Therefore,the setNTn(1,3)={e0,e1,e2,en-2}is the MDRS.AS a result,the Lemma 4.2 holds.

Table 12: The metric coordinate vectors for Tn(1,3),where n=3l,l ≥3

Lemma 4.3.Letn≡1(mod3)forn≥7,we have

Proof.Suppose thatn≡1(mod3)andn≥7.Then,in the casen≡1(mod3)andn=7,the MDRS forT7(1,3)isNTn(1,3)= {e1,e2,e5}.Now, for the casen≡1(mod3) andn ＞7, we need to prove thatSo,finding a DRS having order 4 is sufficient.From Table 10 using the setsSω(e0),the following Table 13 illustrates the metric coordinate vectors for all vertices ofTn(1,3)with respect to the setNTn(1,3)={e0,e1,e2,en-2},wheren=3l+1,andl≥3 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 13 is 0.Using Table 13, we may check that there exist a pair of verticesh1,h2∈Sω(e0)for someω∈{1,2,...,l+1}such as the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=0,holds true.Also,there exist the verticesh1∈Sω(e0)andh2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=ω-ν,holds true.Therefore,the setNTn(1,3)={e0,e1,e2,en-2}is the MDRS.AS a result,the Lemma 4.3 holds.

Table 13: The metric coordinate vectors for Tn(1,3),where n=3l+1,l ≥3

Lemma 4.4.Letn≡2(mod3)forn≥5,we have

Proof.Suppose thatn≡2(mod3)andn≥5.Then,in the casen≡1(mod3)andn=5,the MDRS forT5(1,3)isNTn(1,3)= {e1,e2,e4}.Now, for the casen≡2(mod3) andn ＞5, we need to prove thatSo,finding a DRS having order 4 is sufficient.From Table 10 using the setsSω(e0),the following Table 14 illustrates the metric coordinate vectors for all vertices ofTn(1,3)with respect to the setNTn(1,3)={e0,e1,e2,en-2},wheren=3l+2,andl≥2 be an integer.

It turns out that the value of the first metric coordinate of the vertexe0fromSω(e0)in Table 14 is 0.Using Table 14, we may check that there exist a pair of verticesh1,h2∈Sω(e0)for someω∈{1,2,...,l+1}such as the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=0,holds true.Also,there exist the verticesh1∈Sω(e0)andh2∈Sν(e0)for anyω,ν∈{1,2,...,l+1}such asω/=ν,then the conditionr(h1,NTn(1,3))-r(h2,NTn(1,3))/=ω-ν,holds true.Therefore,the setNTn(1,3)={e0,e1,e2,en-2}is the MDRS.As a result,the Lemma 4.4 holds.

The main theorem is stated below by using Lemmas 4.2-4.4.

Theorem 4.1.LetTn(1,3)be the family of Toeplitz graph,then

Table 14: The metric coordinate vectors for Tn(1,3),where n=3l+2,l ≥2

5 Application

Recently, some applications of DRSs can be seen to localizing the epidemic source in different complex networks such as social networks, epidemics in human beings and the origin of a disease outbreak, etc.(see [38,39]).In particular, we consider a network to reduce the number of observers using the DRSs in order to achieve the perfect detection of an epidemic source.

Let us assume, a social network arranged in the form of Toeplitz networkT11(1,3), where the node setVT11(1,3)= {e0,e1,e2,e3,e4,e5,e6,e7,e8,e9,e10}represents the people and the edge setET11(1,3)={e0e1,e1e2,e2e3,e3e4,e4e5,e5e6,e6e7,e7e8,e8e9,e9e10}∪{e0e3,e1e4,e2e5,e3e6,e4e7,e5e8,e6e9,e7e10}between the nodes represents the links between the people.If the observers are placed throughout the network,and the inter-node distances are reliable and known,a direct solution can be found.But,the entire process would be very costly and time taking.

So,what are the fewest number of observers required to account epidemic source with an unknown starting time and irregular transmission delays among the nodes?Such that each node has a unique representation depending upon minimum distances from the observer nodes.In order to reduce the number of observers,we employed the MDRSNT11(1,3)={e0,e1,e2,e9}of the Toeplitz networkT11(1,3).

By using the Lemma 4.4 and Theorem 4.1,we placed the observers only on the nodese0,e1,e2,e9.It is clear from Table 14 and Fig.4 that each node has a unique representation and epidemic propagation will be optimal by placing observers at the nodese0,e1,e2,e9.This scenario explains the applicability of DRSs in source localization problems.

Figure 4:DRS in T11(1,3)

6 Conclusion

This study is concerned with the concept of calculating MDRSs of graphs using an integer linear programming formulation that has been proposed earlier in the literature.In this article, we theoretically establish the MDRSs for the certain families of Toeplitz graphsTn(1,t)fort= 2, 3, 4 andn≥t+2.We observed that the MD and DMD are equal for the Toeplitz graphsTn(1,2).Also,the DMD for the Toeplitz graphsTn(1,4)is exactly one greater than its MD.In the case ofTn(1,3),the DMD is equal to the MD forn= 5, 6, 7 and is exactly one greater than its MD forn≥8.In future work,certain classes of subdivision graphs of circulant graphsCn(1,k)will be investigated for the MDRS problem.

This research work may lead to the following open problem.

Open Problem 6.1.Investigate the minimal doubly resolving sets for the family of the generalized Toeplitz graphsTn(1,t)for all values oftandn≥t+2.

Acknowledgement:The authors are grateful to the editor and reviewers for the careful reading to improve the manuscript.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.