基于类电磁诱导透明超材料的可调谐慢光器件
沈钊阳,张清河,杨河林,向天宇
(1.三峡大学 湖北省建筑质量检测装备工程技术研究中心,湖北 宜昌 443002;2.三峡大学计算机与信息学院,湖北 宜昌 443002;3.华中师范大学 物理科学与技术学院,湖北 武汉 430050;4.贵州师范大学 大数据与计算机科学学院,贵州 贵阳 550000)
电磁诱导透明现象最初是在原子系统中产生的,是由于其电子在不同路径上相互跃迁所产生的相干过程导致的。它会使得原本不透明介质在某一频段内变得透明,并形成一个谐振窗口[1]。然而在原子系统中实现电磁诱导透明现象需要复杂的实验环境,譬如极低的温度和极强的激光照射。随着超材料的出现,使得电磁诱导透明现象能够在常温常压下被模拟实现[2-4]。它的出现不仅拓宽了电磁诱导透明现象的实现频段,还解决了主动调控的难题。
所谓超材料,指的是由亚波长尺寸的单元结构按周期或非周期排列的一种人工复合材料[5]。通过合理设计超材料的单元结构不仅能够实现对电磁波的调控,而且在完美吸波[6]、极化转换[7]等领域取得了相当多的成果。同时能够模拟一些难以实现的物理现象,如环偶极子、电磁诱导透明等。通常将能够实现类似于原子系统中电磁诱导透明现象的超材料称为类电磁诱导透明超材料。其单元结构主要由两部分组成,分别是明模和暗模,其中明模是指能够与外加电场直接作用产生强辐射,具有较低的品质因数(Quality Factor,Q);而暗模则是无法直接与电磁场相互作用,因此所产生的辐射较弱,具有较大的品质因数[8]。
在2008 年,Zhang 等[9]首次利用超材料在理论上实现了类电磁诱导透明现象,也使得类电磁诱导透明超材料的研究进入了井喷式的发展。譬如Zhu 等[10]利用风车型单元结构的超材料在微波段实现了类电磁诱导透明现象。Han 等[11]则在太赫兹波段研究了一款类电磁诱导透明超材料谐振器,其单元结构由开口谐振环和双金属线组成。然而,上述研究工作只能通过在仿真过程中改变几何参数来实现类电磁诱导透明现象的调控。在这种情况下无法进行实时的调控,是不能被称为具有可调谐性能的,这是由于实物一旦制成其相关几何参数便无法改变。但随着可重构超表面的出现,使得类电磁诱导透明现象的实时调控成为了可能。例如在单元结构的设计中引入了石墨烯[12-14]、光敏材料硅[15]或黑磷[16]等材料,通过在外部加载偏置电压或改变光照强度来实现对电磁诱导透明现象的调控。另一方面,也可以通过使用一些特殊的相变材料,如二氧化钒[17-18]等,其电磁特性可以在改变外界温度的情况下实现金属特性和介质特性的转化,从而控制类电磁诱导透明现象的产生。但由于这些材料的特殊性,使得相关研究主要集中在太赫兹波段。为了在微波段实现类电磁诱导透明超材料的可调控,研究者们通常会在金属结构中加载二极管[19-20],并通过改变外加电压对其进行调控。Feng 等[21]利用传输线超材料模拟了可调控的电磁诱导透明现象,在双开口谐振环上加载变容二极管,随着电容值的变化,谐振峰的频率和幅度产生变化,从而实现了性能的可调控。Bagci 等[22]在TEM 波导中实现了类电磁诱导透明超材料的主动调控,通过改变外加电压实现对变容二极管的电容值的调控,从而控制类电磁诱导透明现象的产生和消失。
基于以上研究背景,本文提出一种能够在自由空间中实现对类电磁诱导透明现象可调控的超材料,不仅能够控制谐振峰的频率和幅度变化,也能够控制类电磁诱导透明现象的产生和消失,使得所设计的超材料具有更加广泛的应用范围。该超材料的单元结构由矩形开缝谐振环和加载变容二极管的开缝金属线组成。通过对透射频谱进行数值仿真表明,其在10.46 GHz处产生了类电磁诱导透明现象,通过改变变容二极管的电容值实现了可调谐的性能,并利用等效电路模型拟合计算出不同电容值下的透射频谱。进一步地,对单元结构的几何参数开展了研究,表明谐振峰的强度与矩形开缝谐振环和加载变容二极管的开缝金属线的相对位置有关。利用表面电流分布和双谐振子模型分析了类电磁诱导透明现象的物理机理,并通过计算群时延指出其良好的慢光效应,可以用于设计可调谐的慢光器件。
1 模型设计和仿真
图1 为该超材料的单元结构示意图,选用相对介电常数和损耗角分别为3.38 和0.0027,厚为0.813 mm 的Rogers RO4003C 介质板,金属结构采用厚度为0.035 mm 的铜(电导率σ=5.96×107S/m)。该单元结构由矩形开缝谐振环和加载变容二极管的开缝金属线组成,其中变容二极管为BBY52-02W,是由一个0.9 Ω 的电阻、一个0.6 nH 的电感和一个可变电容组成。可变电容的取值分别为2.63,1.52,1.15,0.90 和0.76 pF,其电容值会随着外加电压的增大而逐渐减小。对应的几何参数如下所示: 介质板长度P=20 mm,介质板宽度L=13.2 mm,矩形开缝谐振环长度a=16 mm,矩形开缝谐振环宽度b=7 mm,矩形开缝谐振环开缝宽度d=6 mm,矩形开缝谐振环厚度t=0.9 mm,开缝金属线长度c=8.75 mm,开缝金属线宽度n=2.5 mm,开缝金属线缝宽g=1.5 mm。
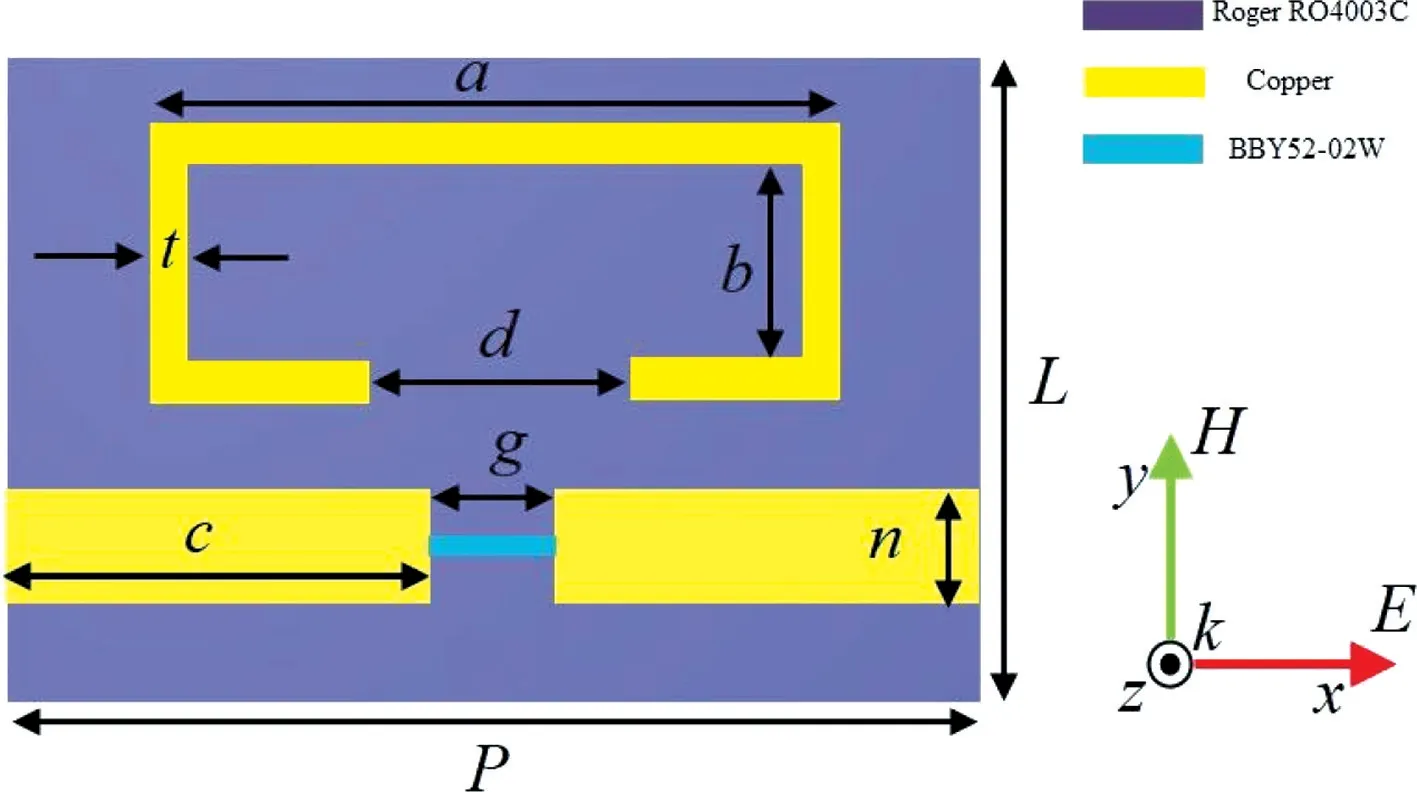
图1 单元结构示意图Fig.1 Schematic of the unit cell
本文中透射频谱的仿真结果是基于电磁仿真软件CST Microwave Studio 中频域仿真所获得的。在仿真过程中将x和y轴方向上的边界条件设置为周期结构,从而满足超材料研究过程中的无限大结构。同时z方向上的边界条件设置为开放边界,使得电磁波从z方向垂直入射至超材料。为了研究该超材料中类电磁诱导透明现象的产生原理,首先仿真计算了单一结构在电磁波作用下的透射曲线,分别是矩形开缝谐振环、开缝金属线和加载变容二极管的开缝金属线。图2(a)为电磁波垂直入射到矩形开缝谐振环时的透射频谱,可以观察到在10.38 GHz 处产生了一个谐振谷,且此时透射系数几乎为0,表明在该频率下电磁波无法通过该结构。当电磁波入射到开缝金属线时,对应的透射频谱如图2(b)所示,在整个频段内透射曲线为一条平滑上升的直线,且透射系数随着频率的增加而从0.26 增加至0.88,证明在该结构中大部分电磁波能够穿透过去。而当变容二极管加载到开缝金属线的开缝处时,透射曲线由上述的平滑直线变为了一条V 型曲线,其中谐振谷的频率和系数分别为10.56 GHz 和0.02(图2(c))。为了比较图2(a)和(c)中所产生的两个谐振谷的特性,可以对比品质因数(Q),其计算公式为Q=f/FWHM,式中f为谐振频率,FWHM 指的是半波长带宽。通过计算可得矩形开缝谐振环和加载变容二极管的开缝金属线的Q值分别为7.21和14.16。
图2 透射频谱的仿真结果。(a)矩形开缝谐振环;(b)开缝金属线;(c)加载变容二极管的开缝金属线Fig.2 The simulation results of transmission spectra.(a)Rectangle split ring resonator;(b)Cut wire;(c)Cut wire loaded variode
首先将矩形开缝谐振环与开缝金属线结合在一起,对应的透射频谱如图3(a)所示。可以观察到透射曲线在10.36 GHz 处产生了一个谐振谷,其频率与单个矩形开缝谐振环在电磁波作用下所产生的谐振谷频率几乎重合。该结果表明两者之间不存在相互作用,因此并未产生类电磁诱导透明现象。图3(b)是矩形开缝谐振环和加载变容二极管的开缝金属线组合时的仿真结果。该透射曲线在10.02 GHz 和10.81 GHz 之间形成一个透射窗并在10.46 GHz 处达到了最高值,对应的透射系数为0.75,表明在该频率下大部分电磁波都能够透过该结构。通过比较这两个结构所产生谐振谷的品质因数可以推断矩形开缝谐振环起着明模的作用,而加载变容二极管的开缝金属线则代表暗模。由此可以证明该超材料所形成的类电磁诱导透明现象是由明模和暗模之间的耦合作用所产生的。由于加载的变容二极管的电容值会随着外加偏置电压的变化而改变,使得透射频谱产生相应的变化,对应的仿真结果如图3(c)所示。随着电容值的减小,透射窗产了红移现象,并且谐振峰的强度也会逐渐降低。譬如当电容值为1.15 pF 时,其谐振峰朝着低频方向移动至9.79 GHz,同时透射系数也降低为0.63;当电容取值0.76 pF 时,透射曲线从原本的透射窗变为了一个V 型曲线,其谐振谷频率为10.51 GHz,表明该超材料在此电容值下无法实现类电磁诱导透明现象。根据图3(c)的仿真结果可以推断该超材料中的类电磁诱导透明现象可以通过调节外加电压来控制谐振峰的频率和透射系数,以及类电磁诱导透明现象的产生或消失,从而实现动态可调的性能。

图3 (a)矩形开缝谐振环和开缝金属线组合时的透射频谱仿真结果;(b)矩形开缝谐振环和加载变容二极管的开缝金属线组合时的透射频谱仿真结果;(c)不同电容值下的透射频谱仿真结果Fig.3 (a)Simulated transmission spectrum of the rectangle split ring resonator combined with the cut wire;(b)Simulated transmission spectrum of the proposed metamaterial;(c)Simulated transmission spectra with different capacitances
2 理论分析
在类电磁诱导透明超材料的设计过程中,单元结构的尺寸参数会对谐振峰的频率或透射系数产生影响。这里分别讨论了矩形开缝谐振环开缝宽度d和加载变容二极管的开缝金属线线宽n对透射频谱的影响。需要指出的是图4 中的所有结果均是在变容二极管的电容值取2.63 pF 时的仿真结果。当其他参数保持不变,d取4,5 和6 mm 时的仿真结果如图4(a)所示,可以观察到整个透射曲线会随着d的增大而产生蓝移现象。换句话说谐振峰的频率会朝着高频方向移动,但其透射系数保持在0.75 左右。图4(b)是固定其他参数为定值,而n则以0.5 mm 为一个增量由2 mm 增加到3 mm时的仿真结果。图中的透射曲线表明谐振峰的频率会随着n的增加从10.65 GHz 移动至10.31 GHz,而相应的透射系数从0.68 增加到了0.78。通过对以上两个仿真结果的分析表明,不同结构的尺寸变化均会对谐振峰的频率产生影响;然而谐振峰的透射系数主要取决于两个结构之间的相对位置。由于加载变容二极管的开缝金属线的线宽变化,使得其与矩形开缝谐振环的距离也产生了变化,而当它们之间的距离越近时,所产生的耦合强度也就越大,从而导致谐振峰的透射性能也越强。

图4 不同几何参数下的透射频谱。(a)d;(b)nFig.4 The transmission spectra with different geometric parameters.(a)d;(b)n
为了探索该类电磁诱导透明超材料的耦合过程,分别观察了两个谐振谷(10.02 GHz 和10.81 GHz)和一个谐振峰(10.46 GHz)处的表面电流分布。为了方便比较,在这三个频率下均选取了相同的电流强度区间。图5(a)是第一个谐振谷处的表面电流分布,可以观察到在该频率下金属结构上的电流密度很小且电流强度十分微弱。这些微弱的电流在加载变容二极管的开缝金属线上形成一个从右往左流动的电流束,而在矩形开缝谐振环上则集中在垂直的金属线两侧。第二个谐振谷的表面电流如图5(c)所示,虽然此时电流密度有所增加,但其电流强度依旧较为微弱,同时这些电流在两个结构上形成了三束同向平行的电流,其方向均为由左往右流动。因此两个结构之间无法形成较强的相互作用。图5(b)为谐振峰处的表面电流分布,此时的电流强度远远高于两个谐振谷处的电流强度。首先表面电流在矩形开缝谐振环上形成了两束由左向右流动的电流束;而在加载了变容二极管的开缝金属线上的电流则是从右往左流动,与矩形开缝谐振环上的电流构成了一对反向平行的电流束。因此可以推断出该超材料中的类电磁诱导透明现象是由矩形开缝谐振环和加载变容二极管的开缝金属线之间的相互作用引起的。

图5 表面电流分布。(a)10.02 GHz;(b)10.46 GHz;(c)10.81 GHzFig.5 The distributions of surface current.(a)10.02 GHz;(b)10.46 GHz;(c)10.81 GHz
为了更进一步地阐述明暗模的耦合机理,接下来用经典的双谐振子耦合模型对该超材料中的类电磁诱导透明现象进行分析。可以将两个谐振子等效为明模和暗模,并用以下公式来表示[23]:
公式(1)和(2)中的x1和x2是谐振幅度,各自的阻尼系数则用γ1和γ2表示,引入的失谐因子δ代表的是谐振频率与固有振荡器的谐振频率之间的差异。外部的激励电场可以表示为E0(t)=E0exp(iωt),明模与此激励电场的耦合强度用g表示,Ω则为两个谐振子之间的耦合强度。结合位移矢量方程xn(t)=xnexp(iωt)(n=1,2) 与频率近似处理2≈2ω1(ω -ω1) 这两个关系式,利用公式(1)和(2)简化可得透射系数与频率之间的关系如下所示[24]:
在本文中ω0表示的是谐振峰的频率10.46 GHz,接着通过拟合计算可得出对应的参数分别为γ1=2.04 GHz,γ2=0.11 GHz,Ω=0.72 GHz,δ=0.16 GHz 和g=1.03 GHz。对应的结果如图6 所示,拟合曲线用虚线表示,其在10.46 GHz 处产生了谐振峰且透射系数为0.68,两个谐振谷的频率分别为9.91 GHz 和10.99 GHz,对应的透射系数均为0.03 左右,与实线所代表的仿真结果较为吻合。从而证明了该类电磁诱导透明超材料是由于明模和暗模之间的耦合所实现的。

图6 基于双谐振子耦合模型的拟合曲线和仿真曲线Fig.6 Transmission spectra from simulation and analytical calculation based on the two-oscillators model
为了更好地阐述变容二极管对所设计的类电磁诱导透明超材料的可调控作用,接下来利用等效电路模型对相关透射曲线进行分析[25]。首先,在单元结构设计中所使用的金属线可以等效为电感,而金属结构间的间隙可以等效为电容,金属的欧姆损耗被等效为电阻。因此金属结构可以等效为一个由电容、电感和电阻串联的RLC 电路。其中明模和暗模的区别在于是否存在有源器件,因为明模是被外加电磁场所激发的,故在等效电路中可以用电源Vs来表示。由此可以得出该超材料的等效电路模型如图7(a)所示,其中矩形开缝谐振环由Vs,R1,L1和C1组成,加载变容二极管的开缝金属线则由R2,L2,C2和R,L,Cv组成的变容二极管BBY52-02W 构成,其中R=0.9 Ω,L=0.6 nH,Cv则是可调电容。需要指出的是,谐振点的频率,因此等效电路模型中电阻的阻值不会影响谐振峰频率的变化,其主要还是受到电容值和电感值的影响。图7(b)~(f)给出了在不同电容值下通过等效电路模型计算出的透射频谱与仿真曲线的对比结果,其中变容二极管的电容值分别为2.63,1.52,1.15,0.90 和0.76 pF,同时计算所得电容和电感的具体数值(L1,C1,L2,C2)列在表1 中。在图7(b)中计算所得曲线的谐振谷频率为10.02 GHz 和10.81 GHz,谐振峰的频率和透射系数分别为10.39 GHz 和0.74,三个谐振点所对应的频率与仿真结果相比存在些许偏移。但对整个透射曲线而言,拟合结果与仿真结果较为吻合。图7(c)是当变容二极管的电容值为1.52 pF 时所对应的透射曲线,虚线代表计算的谐振谷分布在9.89 GHz 和10.62 GHz,其透射系数接近于0,以及对应的谐振峰也与仿真结果十分吻合,在10.09 GHz 处具有将近74%的透射效率。而当电容值变为1.15 pF 时所得的拟合曲线中谐振峰频率偏移至9.89 GHz,与仿真结果存在0.1 GHz 的偏移。而透射系数为0.62,与仿真结果较为吻合,对应的曲线显示在图7(d)中。当变容二极管的电容值降为0.90 pF 时,计算所得的结果在9.69 GHz 处产生了一个谐振峰,而两个谐振谷分别位于9.57 GHz 和10.11 GHz,但其透射系数均为0.2 左右,与仿真结果相比差异主要集中在第二个谐振谷处。图7(f)表示当电容值变为0.76 pF时,类电磁诱导透明现象将会消失,透射曲线形成一条谐振谷。总的来说,通过等效电路模型所计算的透射曲线与仿真结果有很高的匹配度。不仅验证了该超材料中类电磁诱导透明现象是通过明、暗模之间的耦合实现的,也从侧面印证了通过对变容二极管中电容值的调节可以改变谐振峰频率和幅度,同时也可以控制类电磁诱导透明现象的产生或消失,证明其具备可调谐的性能。
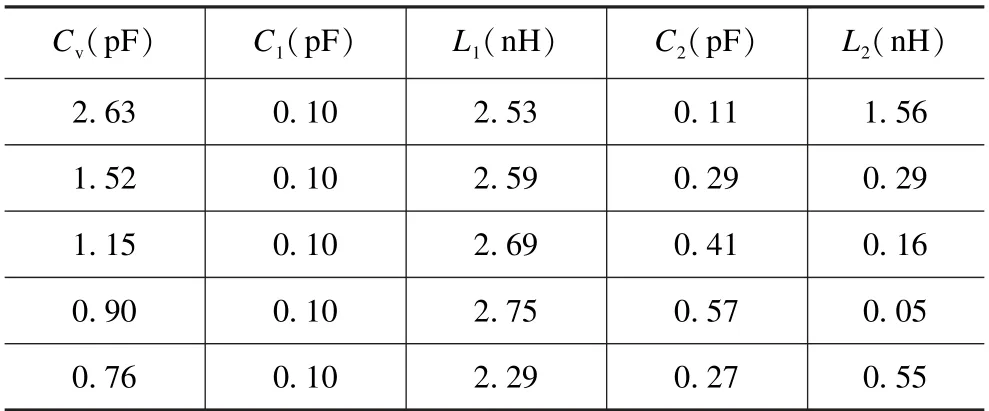
表1 变容二极管取不同电容值时等效电路模型的电容和电感取值Tab.1 Parameters of capacitance and inductance in the equivalent circuit model with different capacitances in variode

图7 (a)等效电路模型;通过等效电路计算的不同电容值下透射频谱: (b)2.63 pF;(c)1.52 pF;(d)1.15 pF;(e)0.90 pF;(f)0.76 pFFig.7 (a) The equivalent circuit model.The transmission spectra based on the equivalent circuit model with different capacitances.(b)2.63 pF;(c)1.52 pF;(d)1.15 pF;(e)0.90 pF;(f)0.76 pF
在类电磁诱导透明超材料中慢光效应是十分重要的性质之一,其往往来源于谐振峰所具有的强色散特性。所谓慢光效应是指电磁波能够在介质中以极低的群速度传播。通常使用群时延(Group Delay,τg)来描述慢光效应的能力,对应的公式为[26]:
式中:φ指的是透射相位的变化;角频率用ω来表示。图8 给出了不同电容值下所设计超材料的透射相位的变化和根据公式(4)计算所得的群时延。图8(a)给出了电容值为2.63 pF 时的透射相位和群时延,可以观察到透射相位在谐振峰处发生了急剧的变化,其相位值在透射窗口的范围内从250°降至100°。正是由于这些相位的变化使得慢光效应能够实现。所计算的群时延在10.46 GHz 处达到了最大值107 ns,表明在该频率下的电磁波可以在自由空间中传播32.1 m,但该类电磁诱导透明超材料的厚度仅为0.848 mm,因此可以印证电磁波的传播速度在该超材料中变慢了,即实现了慢光效应。根据图3(c)的仿真结果可以得出当变容二极管的电容值为1.52,1.15 和0.90 pF 时,透射频谱依旧表现出一定程度的类电磁诱导透明现象,故而仍然具备慢光效应。对应的透射相位和群时延如图8(b)~(d)所示,在这三个电容值下的透射相位均在谐振峰处产生了相位突变现象,且相位都是由高向低变化。同时通过计算可得对应的群时延分别为127,195和163 ns,证明在这三种情况下所设计的超材料依旧具有良好的慢光效应。但当电容值变为0.76 pF 时,透射相位仅仅是在谐振谷处产生了一个由低向高变化的趋势。对应的群时延的计算结果如图8(e)中的虚线所示,其数值在整个频段内的大部分位置都是接近于0 的,且在10.51 GHz 处的群时延达到了-763 ns,故不具备慢光效应。综合以上结果,可以将提出的类电磁诱导透明超材料用于研究可调控的慢光器件。

图8 不同电容值下透射相位和群时延的结果Fig.8 The results of transmittance phase and group delay with different capacitances
3 实验测试
图9(a)是由传统的电路印刷技术制作的实验样品,并在每个开缝金属线上焊接了变容二极管。为了能够同时通过加载电压改变变容二极管的电容值,在介质板的左右两侧引入了两条金属线。整个实验样品由10×14 个单元结构组成,对应的整体尺寸为210 mm× 198 mm。图9(b)是实验测试装置的示意图,在测试过程中使用到了一对双脊喇叭天线,它们分别位于实验样品的两侧,并通过同轴线与矢量网络分析仪(Agilent PNA E8362B)相连。其中一个喇叭作为发射端,另一个则是接收端,从而可以在矢量网络分析仪上获得相透射曲线的实验数据。在实验样品的两端分别用导线连接一个电压源用于加载电压,使得变容二极管的电容值改变。由于实验样品中变容二极管具有串联和并联的关系,为了使所有的电容值都发生改变,会加载较大的电压,考虑到相关的安全因素,这里仅进行了未加载偏置电压和加载20 V 偏置电压的实验测试,相应的实验结果与仿真结果的对比如图9(c)所示。在未加载偏置电压时,透射曲线在9.08~11.63 GHz 之间形成了一个透射窗口,谐振峰的频率为10.91 GHz,且透射系数接近于1,与对应的仿真结果相比,谐振峰的频率偏移了约0.45 GHz。当外加电压增加至20 V 时,变容二极管的电容值变为1.52 pF,此时谐振峰频率移至10.62 GHz,即随着电容值的减少,谐振峰频率往低频方向移动,这种变化趋势与仿真结果相似。同时观察相应透射频谱可以发现,实验结果的谐振峰频移量为290 MHz,仿真结果的频移量为350 MHz,实验结果与仿真结果在一定程度上较为吻合。实验结果表明所设计的超材料具有类电磁诱导透明特性,并且能够通过外加电压实现可调控功能。实验结果与仿真结果之间产生差异的原因可以归纳为以下几点: 首先实验样品的制作工艺误差使得样品结构参数与仿真中的尺寸参数存在一定的差异;另一方面则是实验使用的介质板的介电常数会与仿真中的介电常数有所偏差;还有一部分原因来源于变容二极管,其中实际电路中变容二极管封装带来附加阻抗以及焊接过程对金属结构之间的耦合产生影响;最后由于实验条件有限,周围环境的电磁干扰,甚至电压源产生的电磁信号也会影响实验结果。

图9 (a)实验样品图;(b)实验测试装置的示意图;(c)在外加0 V 和20 V 偏置电压下透射频谱的实验结果与仿真结果对比Fig.9 (a) The experimental sample;(b) The diagrammatic drawing of experiment setup;(c) The comparison between measured and simulated results of transmission spectra under the applied 0 V and 20 V bias voltages
4 结论
本文在微波段设计并实现了可调谐的类电磁诱导透明超材料。通过改变单元结构中变容二极管的电容值来调节谐振峰的频率和幅度变化,甚至控制类电磁诱导透明现象的产生和消失。结合透射相位计算的群时延表明该超材料具备良好的慢光效应,使其在可调控慢光器件的研究和设计中具有潜在价值。通过表面电流分布、双谐振子模型和等效电路模型对类电磁诱导透明现象进行了分析,证明了该超材料中存在明模和暗模,且它们之间存在耦合作用。通过实验测试验证所设计的超材料能够在改变外加电压后实现一定程度的可调性能。该结构的设计思路在太赫兹波段同样具备可行性,并为可调控电磁器件的设计提供理论参考。

