On Some Novel Fixed Point Results for Generalized F-Contractions in b-Metric-Like Spaces with Application

Kastriot Zoto,Ilir Vardhami,Duan Bajovi´c,Zoran D.Mitrovi´c,★and Stojan Radenovi´c

1Department of Mathematics and Computer Sciences,Faculty of Natural Sciences,University of Gjirokastra,Gjirokastra,6001,Albania

2Department of Mathematics,Faculty of Natural Sciences,University of Tirana,Tirana,1001,Albania

3Faculty of Electrical Engineering,University of Banja Luka,Banja Luka,78000,Bosnia and Herzegovina

4Department of Mathematics,Faculty of Mechanical Engineering,University of Belgrade,Beograd,11120,Serbia

ABSTRACT The focus of our work is on the most recent results in fixed point theory related to contractive mappings.We describe variants of(s,q,φ,F)-contractions that expand,supplement and unify an important work widely discussed in the literature,based on existing classes of interpolative and F-contractions.In particular,a large class of contractions in terms of s,q,φ and F for both linear and nonlinear contractions are defined in the framework of b-metric-like spaces.The main result in our paper is that (s,q,φ,F)-g-weak contractions have a fixed point in b-metric-like spaces if function F or the specified contraction is continuous.As an application of our results,we have shown the existence and uniqueness of solutions of some classes of nonlinear integral equations.

KEYWORDS(φ,F)-contraction;(s,q,φ,F)-contraction;b-metric-like space;fixed point

1 Introduction

Fixed point theory has been studied for a long time.Its application relies on the existence of solutions to mathematical problems that are based on the contraction principle.An interesting generalization of the Banach contraction principle was given by Wardowski [1,2] using a different type of contraction calledF-contraction and by Karapınar in [3] defining the type of interpolative contractions.These approaches have been extended by weakening the contractive conditions,removing some of the imposed conditions on the used mappings or relaxing axioms of the defined spaces.Starting from these aspects,many researchers have constructed new fixed point theorems in different types of spaces such as metric,b-metric and other generalized metric spaces, as cited in [3–31].Nevertheless, in the papers of Younis et al.[4,5] the notion of Kanan mappings in the view ofFcontraction in the setting ofb-metric-like spaces has been expanded and an example related to electrical engineering has been given.In this paper, we introduce general types of(s,φ,F)and(s,q,φ,F)-contractions,which are variants of Wardowski contractions in the setting ofb-metric-like spaces.Using these classes of contractive mappings,we establish unique fixed point theorems that unify and extend recent results on this topic.

2 Preliminaries

In this section,we list some well-known definitions and lemmas in terms ofb-metric-like spaces.

Definition 2.1[9].LetVbe a nonempty set ands≥1 be a given real number.A mappingb:V×V→[0,+∞)is called ab-metric-like if for allγ,δ,ν∈Vthese conditions are satisfied:

(i) b(γ,δ)=0 impliesγ=δ;

(ii) b(γ,δ)=b(δ,γ);

(iii) b(γ,δ)≤s[b(γ,ν)+b(ν,δ)].

The pair(V,b)is called ab-metric-like space(in the sequel we useb－m.l.sfor short).

In ab-metric-like space(V,b), ifγ,δ∈Vandb(γ,δ)= 0, thenγ=δ.However, the converse need not be true,andb(γ,γ)may be positive forγ∈V.

Definition 2.2[10].Let(V,b)be ab－m.l.swith parameters≥1,{νn}be any sequence inVandν∈V.Then,the following applies:

Lemma 2.3.[9].Let(V,b),be ab－m.l.swith parameters≥1.Then,the following applies:

(a) Ifb(γ,δ)=0,thenb(γ,γ)=b(δ,δ)=0;

3 Results

We begin the main section with a definition that is an expanding outlook of Wardowski type(φ,F)-contractions in the frame of a generalized metric space such asb－m.l.s.

Definition 3.1.Let(V,b)be ab－m.l.swith parameters≥1 andfbe a self-mapping onV.We say thatfis a(s,q,φ,F)-contraction if there exist the functionsF:(0,+∞)→R andφ:(0,+∞)→(0,+∞)such that

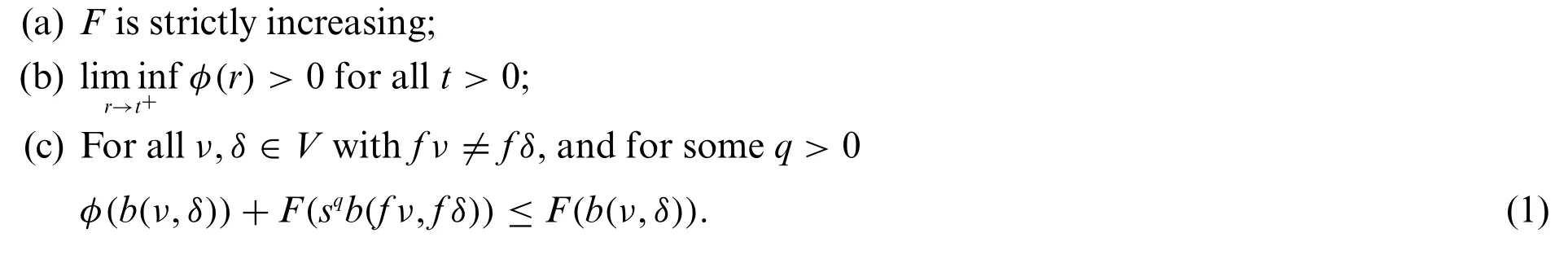
Remark 3.1.In the above definitions propertyFand conditions(1)yield

b(f ν,f δ)≤sqb(f ν,f δ)＜b(ν,δ).

The continuity of the mappingffollows from the inequalityb(f ν,f δ)＜b(ν,δ).

Remark 3.2.

· Our definition generalizes the previous definitions given in [14–16].It contains a reduced number of conditions compared with the previous definitions.

· The definition of(s,q,F)-contraction is an immediate consequence of Definition 2.1,if we takeφ:(0,+∞)→(0,+∞)to be a constant function.

· Ifs=1 we get the definition of Wardowski in[1,2]in the case of metric spaces.

· Fors=1 the definition is valid in the framework of a metric space.

The following is the first fixed point theorem for(s,q,φ,F)-contraction type mapping.

Theorem 3.1.Let(V,b)be a completeb－m.l.swith parameters≥1.Iffis a(s,q,φ,F)-contraction onV,then the functionfhas a unique fixed point inV.

Proof.Let beν0∈Vand the Picard iterative sequence {νn} defined byνn+1=f(νn)forn∈{0,1,2,...}.The proof is clear in the case that there existsn0∈N,withνn0+1=νn0.So,we will assume thatνn+1νn,which impliesf νnνn－1andb(f νn,f νn－1)＞0,for alln∈N ∪{0}.Using inequality(1),we have

Further from inequality(2),we get

sqb(νn,νn+1)＜b(νn－1,νn),

which implies

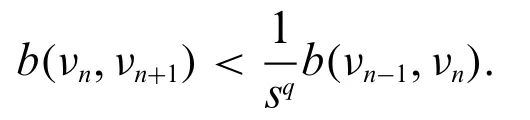
According to the(1),it follows:

that from property ofFwe get

From triangular property and(4),we have

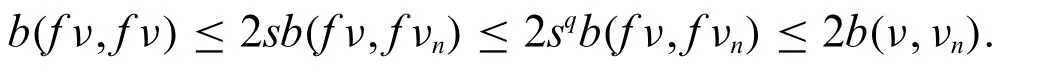
Sincefis continuous and using(3),(4)we obtain

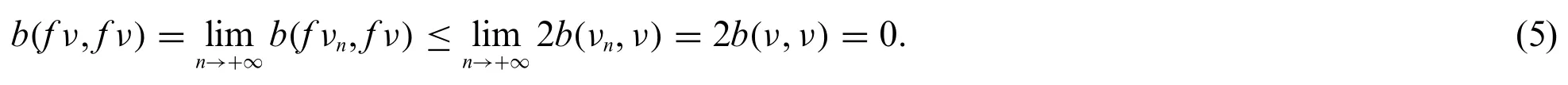
Sinceb(ν,f ν)≤s[b(ν,f νn)+b(f ν,f νn)],asn→+∞we obtain thatb(ν,f ν)= 0.Thusf ν=νand sofhas a fixed point.Also from(3),we haveb(ν,ν)= 0.To prove the uniqueness of the fixed point,suppose thatu∈Vis another different fixed point.Fromuνfollowsfuν,then

which implies

Previous inequality is a contradiction,sob(u,ν)=0 and the fixed point is unique.

Corollary 3.1.Let(V,b)be ab－m.l.swith parameters≥1 andfbe a self-mapping onV.If there exist an increasing functionF:(0,+∞)→R and a positive constantτsuch that

for allν,δ∈Vwithf νf δ,and for someq ＞0,thenfhas a unique fixed point inV.

Proof.Inequality(1)implies(6)if we setφ(r)=τ ＞0.

Example 3.1.LetV= [0,+∞)andb(x,y)=x2+y2+|x－y|2,for allx,y∈V.It is clear thatbis ab-metric-like onV, with parameters= 2 and(V,b)is complete.Also,bis not a metric-like norb-metric(nor a metric onV).Consider the self-mappingf:V→Vbyfx=For allx,y∈Vand constantq=2,we have

Taking the logarithms in the above inequality and fixingτ= ln 5 and the functionF(t)= lntthen the conditions of Corollary 3.1 are satisfied and clearlyx=0 is a unique fixed point off.

With the aim of expanding the initiated Definition 2.1 and starting a result that includes Theorem 3.1 and its respective corollaries,we will use a class of implicit relations,which makes simultaneously effective enormous literature on this topic.

LetΓ4be the set of all continuous functionsg:[0,+∞)4→[0,+∞)satisfying

(a)gis non-decreasing with respect to each variable:

(b)g(t,t,t,t)≤tfort∈[0,+∞).

Definition 3.2.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a self mapping.We say thatfis generalized(s,q,φ,F)-g-weak contraction,if there exist functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)andg∈Γ4such that

for allx,y∈Vwithfxfy,and for someq≥1.

Remark 3.3.

· The above definition reduces to a generalized(s,q,F)-g-weak contraction by settingφ:(0,+∞)→(0,+∞)to be a constant functionφ(r)=τ ＞0.

· Fixing the parameters=1 we get the definition of(φ,F)-g-weak contraction in the setting of metric and metric-like spaces.

· Fixings=1 andφ(r)=τ ＞0 we get the definition of(F-g)-weak contraction in the setting of metric and metric-like spaces.

Theorem 3.2.Let(V,b)be ab－m.l.swith parameters≥1 and the self mappingf:V→Vbe a generalized(s,q,φ,F)-g-weak contraction.IfforFis continuous,thenfhas a unique fixed point inV.

Proof.Letu0∈Vbe arbitrary and construct the Picard iterative sequence{un}asun+1=f(un)forn∈{0,1,2,...}.The proof is clear in the case that there existsn0∈N,withun0+1=un0.Therefore,we assume thatun+1un,which meansf umf un－1orb(f un,f un－1) ＞0 for alln∈N ∪{0}.Using(7)forx=un,y=un－1we have

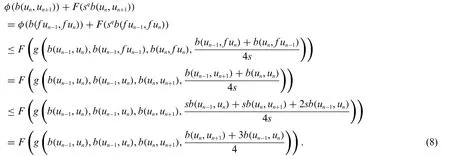
If we assume thatb(un－1,un)≤b(un,un+1),then inequality(8)yields

φ(b(un,un+1))+F(sqb(un,un+1))≤F(g(b(un,un+1),b(un,un+1),b(un,un+1),b(un,un+1)))

≤F(b(un,un+1)),

for alln∈N.So,we obtain

F(sqb(un,un+1)≤F(b(un,un+1))－φ(b(un,un+1))

＜F(b(un,un+1)),

which is a contradiction.Therefore

b(un,un+1)＜b(un－1,un),

for alln∈N.Thus,the sequence{b(un－1,un)}is decreasing and bounded below.Consequently,there existsl≥0 such thatb(un－1,un)→lasn→+∞.Ifl ＞0,then by taking the limit in(8)we get

φ(l)+F(sql)≤F(l),

which is a contradiction.Therefore,we conclude thatl=0 and

From condition(7),we get

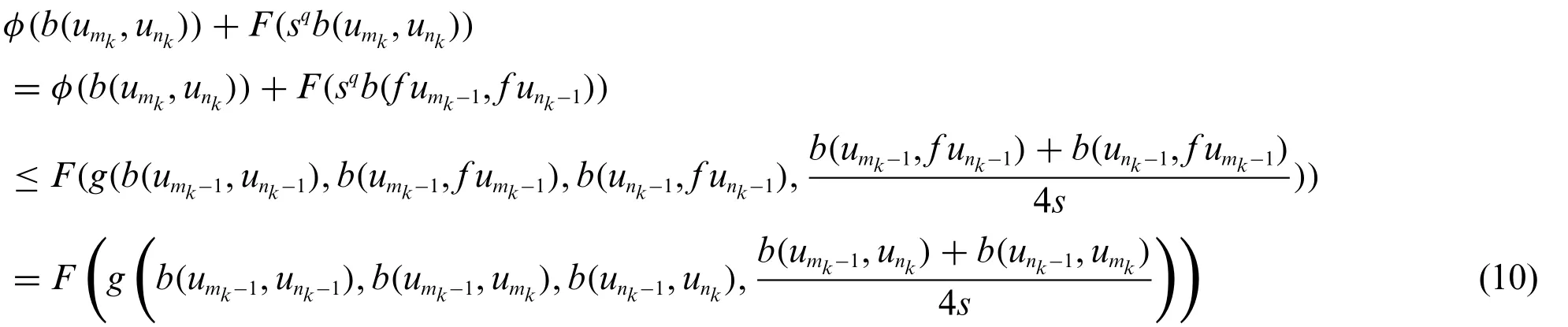
Taking the upper limit in(10)ask→+∞and using Lemma 2.3,Lemma 2.4 and(9),we get

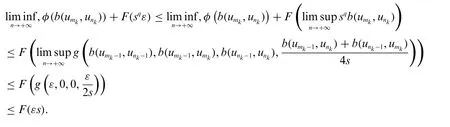
Hence,the acquired inequality

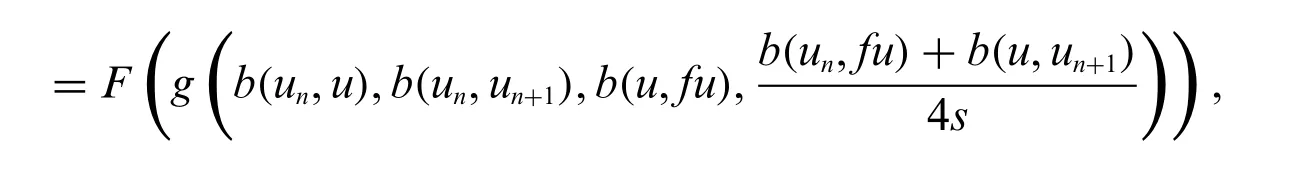
which implies

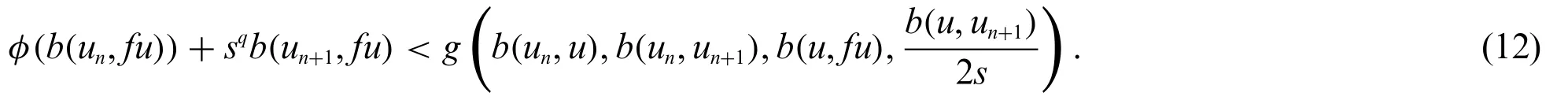
Taking the upper limit in(12),and using Lemma 2.1 and result(9),it follows that

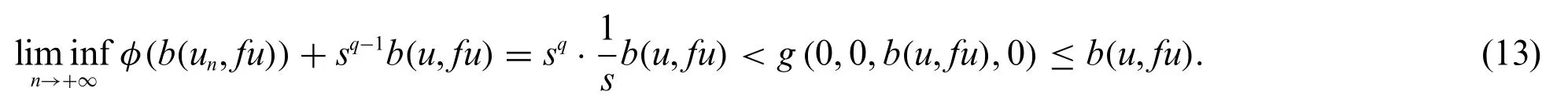
Sinceq≥1,the inequality(13)impliesb(u,fu)= 0 and thereforefu=u.Thus,uis a fixed point and

Letuandvbe two fixed points off,wherefu=uandfv=v.Sinceuv,it impliesfufv.By(7)we have

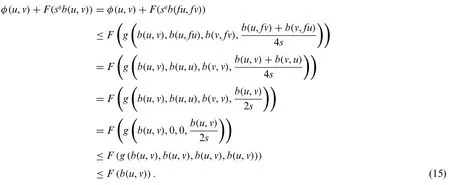
Since this is a contradiction,it impliesb(u,v)=0.Therefore,u=vand the fixed point is unique.

Theorem 3.3.Let(V,b)beb－m.l.swith parameters≥1 andf:V→Vbe a continuous selfmapping.Assume that there exist the functionsF:(0,+∞)→R,g∈Γ4and the constantτ ＞0 such that

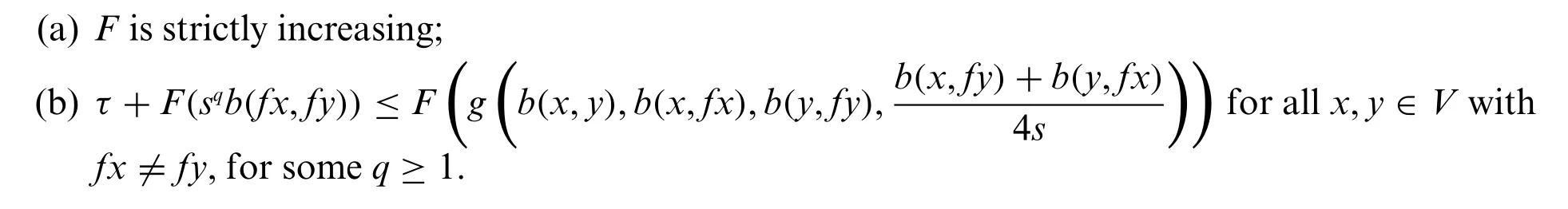
Thenfhas a unique fixed point inV.

Proof.The proof follows from Theorem 3.2.by settingφ(r)=τ.

Corollary 3.2.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that:

for allx,y∈Vwithfxfy,and for someq≥1.Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈Γ4asg(t1,t2,t3,t4)=max{t1,t2,t3,t4}.

Corollary 3.3.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that:

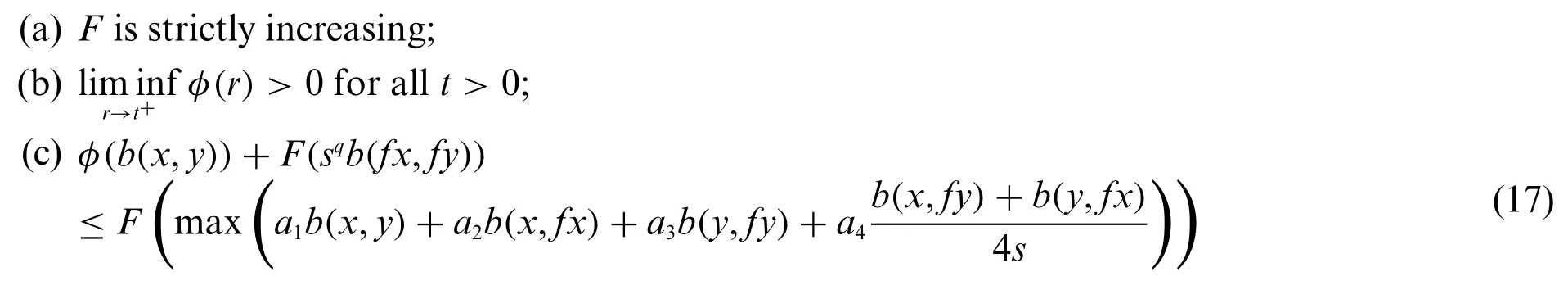
for allx,y∈Vwithfxfy,and for someq≥1.Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2.by takingg∈Γ4asg(t1,t2,t3,t4)=a1t1+a2t2+a3t3+a4t4with 0＜a1+a2+a3+a4＜1.

Recently,many authors have studied new types of contractions known as interpolative contractions and hybrid contractions.The reader can refer to[3,11,17–21].The rest of the paper deals with this type of contractions extended in the setting ofb-metric-like spaces,which can be obtained from our results as a certain special cases.

Theorem 3.4.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that

for allx,y∈Vwithfxfy,and for someq≥1.Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈Γ4as

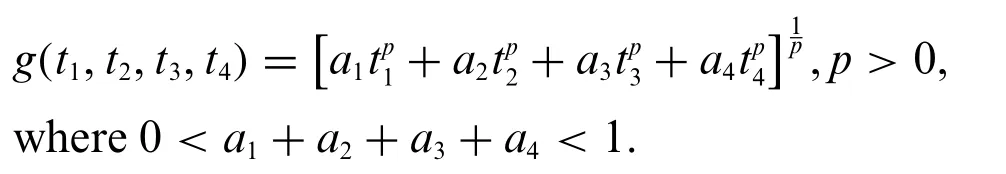
Theorem 3.5.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that

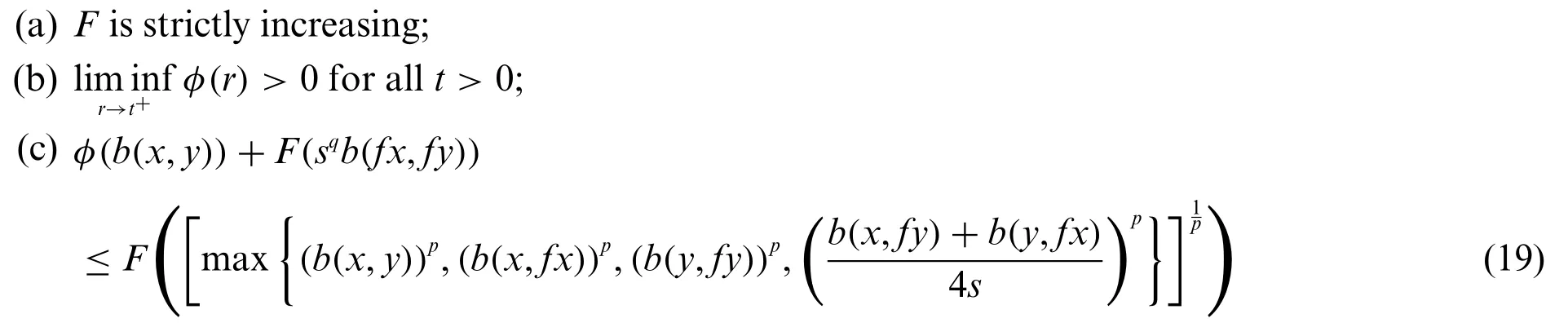
for allx,y∈Vwithfxfy,and for someq≥1.

Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈Γ4as

Theorem 3.6.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that:

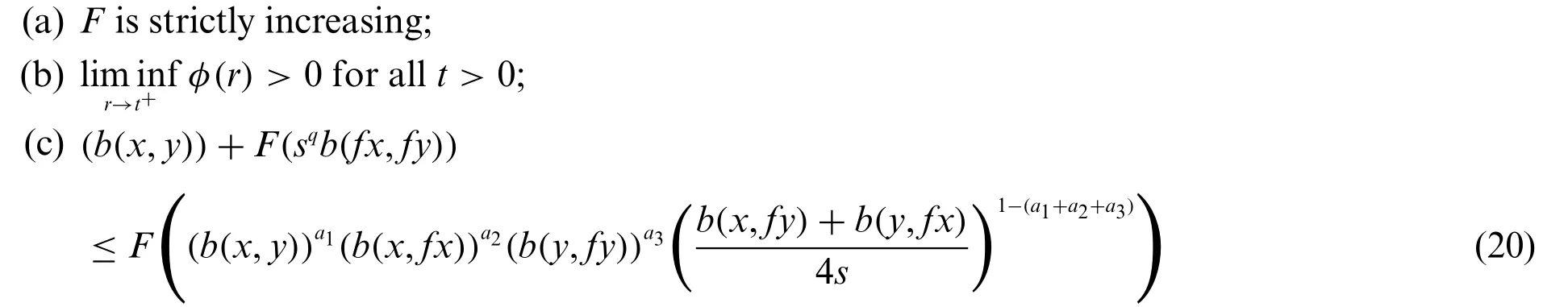
for allx,y∈Vwithfxy,and for someq≥1.

Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈Γ4as

wherea1,a2,a3∈(0,1)anda1+a2+a3＜1.

Theorem 3.7.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)andλ∈(0,1)such that

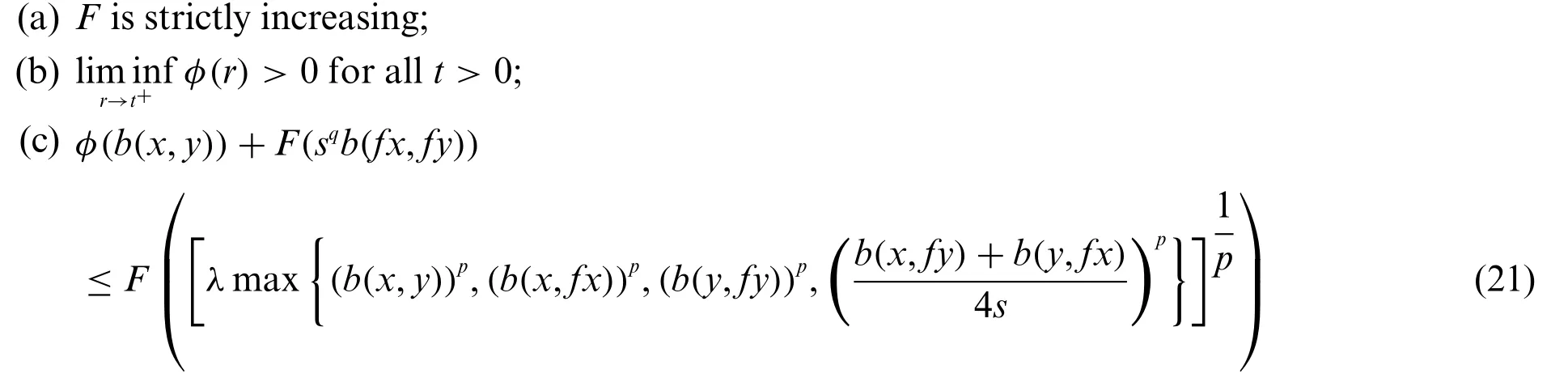
for allx,y∈Vwithfxfy,and for someq≥1.

Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈Γ4asg(t1,t2,t3,t4)=[λmaxp ＞0,λ∈(0,1).

Corollary 3.4.Let(V,b)be ab－m.l.swith parameters≥1 andf:V→Vbe a continuous self-mapping.Assume that there exist the functionsF:(0,+∞)→R,φ:(0,+∞)→(0,+∞)such that

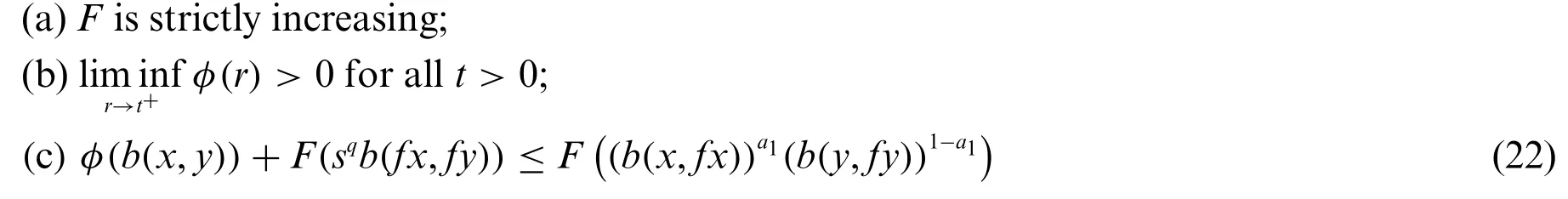
for allx,y∈VF(fix(f))withfxfy,for someq≥1.

Thenfhas unique fixed point inV.

Proof.The proof follows from Theorem 3.2 by takingg∈wherea∈(0,1).

Remark 3.4.

· Varieties of further results can be obtained by extending the setΓ4toΓ5,Γ6,Γ7,etc.

· Many significant fixed point theorems that were established for types of interpolative and hybrid contractive conditions essentially belong to the class of generalized(φ,s,q,F)-g-contractions.

4 Application

The study of the existence,nonexistence and uniqueness of the solution of differential and integral equations,plays a fundamental role in the research on nonlinear analysis and engineering mathematics.One of the main tools developed in this area consists of the application of a fixed point method.

Let us study the existence of solution for the nonlinear integral equation

whereλiare positive constants and functionsGi:[0,1]×[0,1]→R+,Hi:[0,1]×R →R fori=1,2 are given.

LetV=C([0,1])be the set of real continuous functions defined on [0, 1] endowed with theb-metric-like

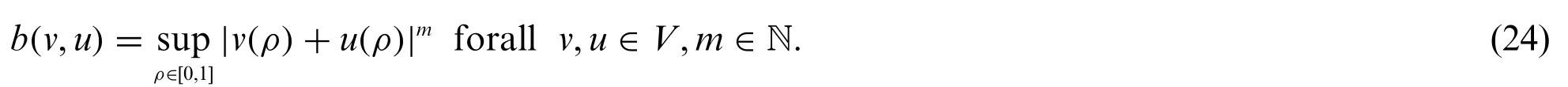
It is obvious that(V,b)is a completeb-metric-like space with parameters=2m－1.

Consider the mappingf:V→Vby

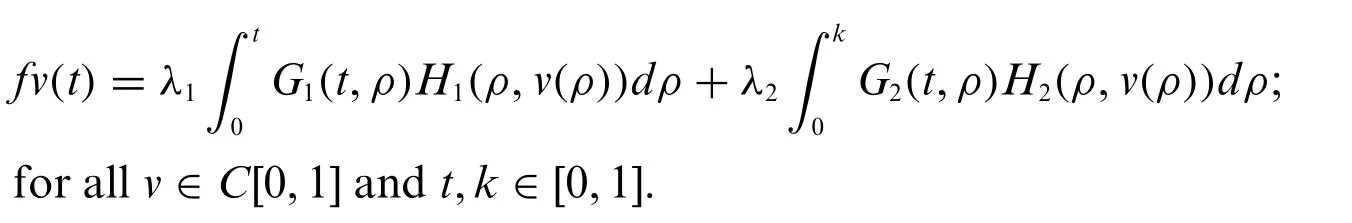
Theorem 4.1.Consider the integral Eq.(1)via the following assertions:

i.The mapping f :V →V is continuous;

ii.Hi:[0,1]×R →R are continuous and there exist constants Aisatisfying

Hi(ρ,v(ρ))+Hi(ρ,u(ρ))≤Ai|v(ρ)+u(ρ)|

for i=1,2 and t,ρ,k ∈[0,1];

iii.The constants λi,Aiand functions Gi,for i=1,2 satisfy condition

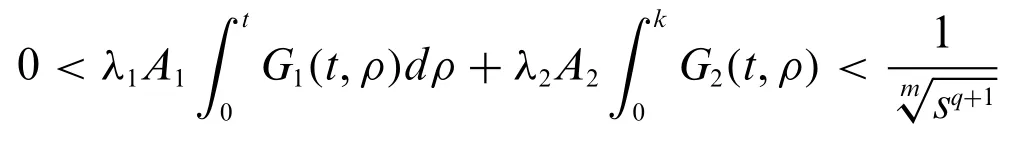
for t,k ∈(0,1)and q ≥1.Then the integral Eq.(23)has a unique solution v(t)∈V.

Proof.For all t ∈[0,1],and v,u ∈V we have

Hence,by taking logarithms in inequality(25)we get

ln s+ln(sqb(fv,fu))≤ln(b(v,u)).

Further,fixingF(ζ)=ln(ζ),τ=lnsand takingg∈Γ4asg(t1,t2,t3,t4)=t1we obtain

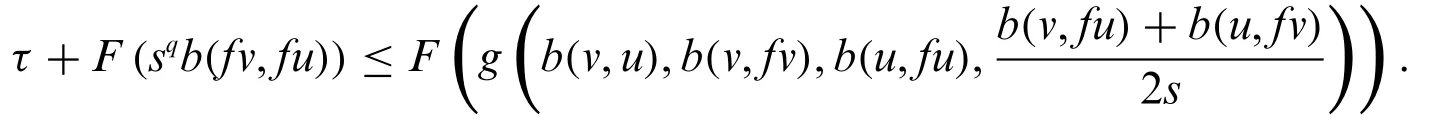
Therefore,fis a(s,q,F)-g-contraction onVand all conditions of Theorem 3.3 are satisfied.Thus,v(t)is the unique fixed point off,i.e.,the solution of the integral Eq.(23).

5 Conclusion

The Definitions 2.1 and 3.2 not only a large class of contractions in terms ofφ,s,q,gandFin the metric,b-metric, metric-like, partial metric, but also have a unifying power for both linear and nonlinear contractions in the framework ofb-metric-like spaces.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The author declares that they have no conflicts of interest to report regarding the present study.