具有非单调发生率的随机离散SIR传染病模型的稳定性

谭伟,刘茂省

(中北大学 理学院,太原 030051)

自古以来,人类就饱受各种传染病的困扰.通常,传染病可以通过空气、水、食物、接触、垂直传播(母婴传播)、体液传播等方式在人与人之间或人与动物之间广泛传播.传染病不但会影响人们的正常生活,人们的生命安全还会遭受严重威胁.因此,传染病的预防和控制已成为研究的热点.

传染病研究的开始,人们普遍认为是Daniel Bernoulli在1760年对天花疫苗接种的研究,对确定性传染病数学模型的研究早在20世纪初就开始了.直到1927年,文献[1-2]在研究伦敦流行的黑死病时提出了SI舱室模型,然后在1932年建立了SIS模型,对传染病动力学的研究做出了重要的贡献.之后许多学者对一些传染病模型进行了广泛的研究,例如SIS模型和SIR模型[3-6].且SIR传染病模型是传染病动力学中重要的数学模型之一[4-6].近几十年来,许多学者建立了基于具有随机扰动的确定性模型的随机流行病模型[6-8],并在近年来,越来越多的学者关注到差分方程模型[9-11].然而,大多数的学者都是将随机模型和离散模型分别建模来研究的,如文献[6,11],在流行病学中对差分方程所描述的随机离散模型的稳定性的研究很少.所以在本文中,主要是对随机离散的传染病模型进行研究.

1 准备知识

一般的确定性SIR传染病模型可以用以下常微分方程来表示[12]:

(1)

其中,S(t),I(t)和R(t)分别代表t时刻易感者、染病者和恢复者的数量.α为种群的招募率,β为疾病的传播率,μ为人群的自然死亡率,γ为感染个体的恢复率,α,β,μ,γ均为正参数.

传染率在流行病学中对研究起着至关重要的作用,改进流行病中的传染率更利于刻画传染病的传播机制.现实中的情况是,随着时间的推移,当传染病开始暴发时,政府实施的各种防治策略和个人预防和控制疫情的意识逐渐增强,从而对疫情的发病率有更强的抑制作用.为了使系统(1)具有更好的现实意义,在系统(1)的基础上,文献[12]进一步研究了具有非单调发生率的SIR传染病模型.模型能被表示为:

(2)

假设随机扰动强度与状态S(t)和状态I(t)在平衡点处的偏差成正比,也就是说当系统状态偏离平衡点的偏差增加时,随机扰动强度也会增加[18].并且这种随机噪声已经被许多学者应用于不同的数学模型[19-20].在上述假设下,将系统(2)加上随机白噪声后的表达式为:

(3)

通常用Euler-Marryama方法[21]对连续模型进行离散化,这种方法在之前就已经被许多学者所应用[22-23].现在对系统(3)用Euler-Marryama方法进行离散化,得到:

(4)

其中h>0是时间步长,且初始条件为S(0)=φ1(0),I(0)=φ2(0).并且在完备的概率空间(Ω,F,P)中,Fn∈F,n∈Z=(0,1,2,…)是一个σ代数簇.通常由E来表示数学期望,ωi(n+1)(i=1,2)(n∈Z)是一个在F中相互独立的随机序列且服从标准正态分布,并且对于ωi(n+1)(i=1,2,n∈Z),满足

(5)

因为系统(4)中有关R的第3个式子并不影响对其动力学行为的研究,所以将其忽略,只对以下系统进行研究:

(6)

对系统(6)的正平衡点Ee进行平移变换,u(n)=S(n)-S*,v(n)=I(n)-I*.然后可以得到以下系统:

(7)

系统(7)的零解与系统(6)的正解Ee=(S*,I*)是等价的.

将正平衡点进行平移变换到原点后,然后在点u(n)=0,v(n)=0处对系统(7)进行线性化.就可以用以下形式来表示系统(6)在平衡点Ee=(S*,I*)下的线性近似系统:

(8)

(9)

(10)

令φ(n)=(u(n),v(n))T,z(n)=(x(n),y(n))T,φ(n)=(φ1(n),φ2(n))T,T代表转置.

为了更好地研究系统的动力学行为,将引入文献[24] 中的一些重要的定义和定理.

定义1(文献[24]定义7.1) 系统(7)或(9)是依概率稳定的,如果对任意的ε1>0和ε2>0存在一个δ>0使得系统(7)或(9)的解φ(n)=φ(n,φ)满足不等式P{supn∈Z|φ(n)|>ε1}<ε2对任意初始函数S(0)=φ1(0),I(0)=φ2(0)使得P{|φ|<δ}=1.

对一个任意的非负函数Vi=V(i,z(0),z(1),…,z(i)),i∈Z,定义ΔVi为

ΔVi=V(i+1,z(0),z(1),…,z(i+1))-V(i,z(0),z(1),…,z(i)).

定理1(文献[24]定理1.1) 对于线性系统(8)或(10),若存在一个非负函数Vi=V(i,z(0),z(1),…,z(i))满足条件EV(0,φ)≤c1‖φ‖2和EΔVi≤-c2E|z(i)|2(i∈Z),其中c1和c2是正常数.那么系统(8)或(10)的零解是渐近均方稳定的.

现在考虑以下的随机差分系统:

(11)

其中σ1,σ2是常数,ωi(n+1)(i=1,2)是Fn自适应随机变量的相互独立的序列且满足条件(5).可以看出系统(8)和(10)的一般形式就是系统(11),因此,为了更加简便地研究系统(11)解的稳定性,令

(12)

矩阵P和D是对称矩阵.对于实对称矩阵P和Q来说,若P-Q是一个正定矩阵,那么P>Q.

定理2(文献[24]中定理5.1) 假设存在一个正定矩阵P,使得一个形式为(12)的半正定矩阵D满足矩阵方程ATDA-D=-P的解,且矩阵P满足

(13)

那么系统(11)的零解是渐近均方稳定的.

证明借助式(12),可以将系统(11)表示为:

z(n+1)=(A+θ(ω(n+1)))z(n),

其中

考虑Lyapunov函数V(n)=zT(n)Dz(n),所以有

ΔV(n)=V(n+1)-V(n)=zT(n+1)Dz(n+1)-zT(n)Dz(n).

然后计算ΔV的期望,得到:

EΔV(n)=E(zT(n+1)Dz(n+1)-zT(n)Dz(n))=EzT(n)[(A+θ(ω(n+1)))TD(A+

θ(ω(n+1)))-D]z(n)=EzT(n)[ATDA-D+θT(ω(n+1))Dθ(ω(n+1))]z(n)=

EzT(n)[-P+θT(ω(n+1))Dθ(ω(n+1))]z(n).

根据式(5),可以求得:

然后根据式(13),可以得到:

其中c是正数,所以凭借定理1,可以得出系统(11)的零解是渐近均方稳定的.证明完成.

接下来,将应用定理2来研究系统(6)的正平衡点和边界平衡点的稳定性.

2 正平衡点的稳定性

现在应用定理2来分析系统(8),它是式(11)的一种特殊形式,在这种情况下,系统(8)的系数矩阵是

(14)

因为ATDA-D=-P,所以可以得到:

(15)

将矩阵A的元素带入式(15)中有

(16)

根据式(13),可以得到:

(17)

然后有以下推论.

推论1若存在一个正定矩阵P,使得条件(17)对于矩阵方程(16)的解(d11,d12,d22)被满足,并且矩阵D是半正定的,那么系统(8)的零解是渐近均方稳定的.因此,对系统(7)的零解来说其就是依概率稳定的,这等同于系统(6)的正平衡点Ee是依概率稳定的.

α=4,μ=0.06,γ=0.01,β=0.2,δ=0.2,h=0.1.

(18)

并将易感个体和染病个体的初始值设为

S(0)=80,I(0)=20.

(19)

正平衡点Ee可以通过以上参数值算得Ee=(S*,I*)=(39.18,23.56).通过求解(14)得到:

对于正定矩阵P,取p11=p22=1,p12=0,所以有

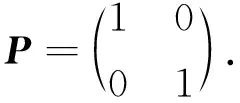
且半正定矩阵D通过求解(16)式得到:

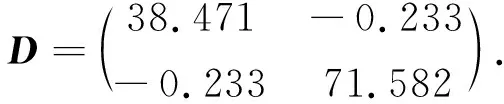
借助推论1,可以了解到如果σ1,σ2满足以下条件:

(20)

那么,系统(8)的零解是渐近均方稳定的.因此,是依概率稳定的对于系统(7)的零解,这等同于是依概率稳定的对于系统(6)的正平衡点Ee.

接下来,将验证之前的阐述借助数值仿真.在图1中展示了噪声扰动强度σ1=σ2=0的情况,图1(a)和图1(b)分别表示系统(6)和线性系统(8)的解曲线.

如图1所示,图1(a)中线性系统(8)的解曲线最终收敛到0.图1(b)中系统(6)的解曲线最终收敛于正平衡点Ee=(S*,I*)=(39.18,23.56).因此,通过观察图像也可以得出系统(8)的零解是渐近均方稳定的,系统(6)的正平衡点Ee是依概率稳定的.

然后将对加入噪声扰动的系统(6)的解进行模拟.借助式(18)和(19)中已给出的参数值和初始值,并且假设σ1,σ2的值满足条件式(20),取σ1=σ2=0.35,具有噪声扰动的系统(6)的解轨迹就可以被得到.

从图2中可以看出,随机噪声并不影响曲线的最终走向,系统(6)的解轨迹最终还是收敛到正平衡点Ee,这就表明系统(6)在正平衡点处是依概率稳定的.

3 边界平衡点的稳定性

研究边界平衡点E0=(S0,I0)的稳定性将要借助线性系统(10).类似地,将定理2应用于系统(10),在这种情况下,系统(10)的系数矩阵为

(21)

将矩阵A的元素带入式(15)中,然后得到

(22)

与推论1类似,根据式(17),以下推论可以被得到.

推论2对于线性系统(10)的系数矩阵(21),如果存在一个正定矩阵P,使方程(22)的解(d11,d12,d22)满足条件(17),且矩阵D为半正定的,则系统(10)的零解是渐近均方稳定的.因此,系统(9)的零解是依概率稳定的,这也就是说系统(6)的边界平衡点E0是依概率稳定的.

当所选择的参数不满足正平衡点存在的条件时,系统(6)中只有一个边界平衡点.在这里,取以下参数值:

α=4,μ=0.1,γ=0.9,β=0.01,δ=0.2,h=0.1.

(23)

并且初始值仍为式(19)中所给出.

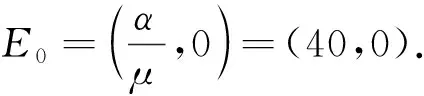
同样,对于正定矩阵P,仍取p11=p22=1,p12=0,得到

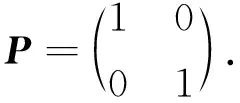
半正定矩阵D的具体形式通过求解方程(22)求得:

并且如果σ1,σ2满足以下条件:

(24)

那么,根据推论2,可以得出系统(10)的零解是渐近均方稳定的.因此,是依概率稳定的对于系统(9)的零解,这等同于是依概率稳定的对于系统(6)的边界平衡点.

根据式(23)中的参数值和式(19)给出的初始值,当随机扰动强度为0时,得到系统(6)和(10)的解曲线.如图3中的(a)和(b)所示.

如图3所示,图3(a)中线性系统(10)和图3(b)中系统(6)的解曲线最终都分别收敛到它们的平衡点.因此,通过图像,也可以得到系统(10)的零解是渐近均方稳定的,而系统(6)的边界平衡点E0是依概率稳定的.

当随机噪声强度不为0,且σ1和σ2的值满足条件(24)时,取σ1=σ2=0.4,参数值和初始值仍为式(23)和(19)中给出,然后可以得到具有随机噪声扰动的系统(6)的解轨迹.

如图4所示,可以看到,具有噪声扰动的系统(6)的解轨迹最终收敛于边界平衡点E0=(40,0),这也表明系统(6)的边界平衡点是依概率稳定的.

并且P仍为单位矩阵,此时求得矩阵D为

然而,矩阵D不是一个半正定矩阵,因此根据推论2,在这种情况下系统(6)的边界平衡点是不稳定的.

如图5所示,发现当随机噪声强度为0时,图5中代表染病者的曲线I是趋向于无穷的,所以此时系统(10)的零解是不稳定的.

然后在这种情况的基础上加入随机扰动.如图6中,当加入一个较小的噪声强度后,发现此时系统的解轨迹在图中是非常不规则的.因此,当一个正平衡点存在时,无论随机扰动是否存在,对于系统(6)来说,它的边界平衡点都是不稳定的.

4 结 论

本文基于一个具有非单调发生率的SIR传染病模型,考虑到疾病在传播过程中不可避免地受到一些随机因素的影响,在系统中加入一个随机扰动项,并假设随机扰动强度与状态S(t)和I(t)偏离平衡点的偏差成正比.通过应用欧拉方法离散化系统,得到一个随机离散系统.用Lyapunov函数方法证明了系统在平衡点处稳定的充分条件.之后,论证了随机离散SIR传染病模型在正平衡点和边界平衡点处的稳定性.

最后,应用数值仿真对正平衡点和边界平衡点的稳定性进行了验证.当所选参数和噪声强度满足给定条件时,发现适当的噪声强度不会影响系统在平衡点处的稳定性.并且还发现,当正平衡点存在时,无论随机扰动强度是多少,边界平衡点的稳定性都不会被改变,并且在这种情况下,边界平衡点是不稳定的.