题组变换做“加法”，问题解决做“减法”

徐羽 万妍青

［摘  要］ 教师在日常教学中要善于引导学生在解决复杂几何问题时，加强对基本图形变化本质的理解，注重培养学生的逻辑推理和直观想象能力，能从同类型问题中总结出基本模型并加以运用.文章以“正方形背景下的几何证明”为例，通过抓住同类型问题的本质特点，通过题组变式，并加以归纳推广，从而助力学生解决问题.

［关键词］ 正方形；几何证明；题组变换

对于几何证明，学生容易产生畏惧心理，尤其当图形复杂或条件繁多时，就会比较慌乱，没有解题思路. 笔者曾对本校学生进行过《优化问题设计对提升专题复习效率》的问卷调查，学生对于几何证明感觉难以解决的原因如图1：

通过分析，可以发现几何证明常涉及四边形与相似三角形、全等三角形的综合，图形比较复杂，对于学生的识图、研图、解图能力要求较高；同时有些题型涉及辅助线的添加，对于学生综合分析、应用能力的要求更高. 由于学生在几何证明中，没有归纳常见的数学模型，没有积累常见的基本解题方法，故只要题目稍加变式，就会变得一筹莫展.

鉴于此，在日常教学中，教师需要将一些典型证明题以题组的形式进行呈现，对题组做“加法”，即抽象基本模型（如A型、X型、子母三角形等），规范基本解法（如利用比例線段、锐角三角比、构造全等或相似等），力求一题多解或多题一解，当对一道例题进行完整的剖析，自然能培养学生化难为易、举一反三的能力. 当学生面对类似背景时，就能够很自然地抽丝剥茧、化繁为简，在问题解决的时候做“减法”，最终掌握解决此类问题的通识通法. 笔者以“正方形背景下的几何证明”为例进行阐述.

问题背景

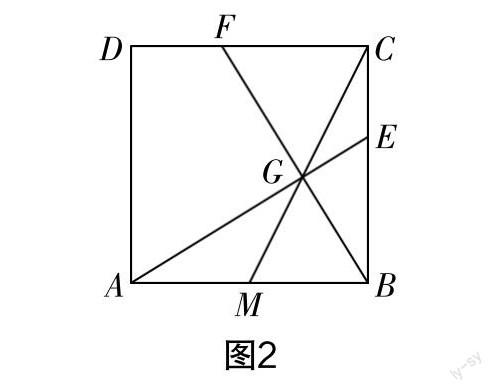
例题  如图2，已知正方形ABCD，点M是边AB的中点，连结CM. 若点G在线段CM上，且∠AGB=90°，延长AG，BG分别与边BC，CD相交于点E，F.

求证：（1）BE=CF；（2）BE 2=BC·CE.

例题分析

1. 识图，寻找边、角数量关系

在识图阶段，学生应该将条件中的文字语言和图形语言建立有机联系，抓住关键文字、几何关系，并迅速在脑海中建立其对应的基本图形，以及联想该图形特有的性质、结论，为最终获得结论奠定基础.

2. 研图：建立已知、未知间的桥梁

在识图环节，学生已经发现图形中边、角的数量关系，并将文字语言和图形语言转化为符号语言. 那么在研图环节，学生需要做的就是通过整合这些数量关系，从而通过新的隐性结论探索与未知结论的联系，找到问题解决的方案.

例题中第（1）问比较简单，结论需要证明BE=CF，而BE和CF位于两个全等的三角形中，因此通过“全等三角形对应边相等”即可得到结论. 利用正方形的性质以及结论②即可得到△ABE≌△BCF（ASA），继而得到BE=CF.

例题中第（2）问的结论BE2=BC·CE是一个等积式. 如图3，借助目标分析法，我们发现对于等积式的证明往往有以下两种方法：找到一组相似三角形，其对应边成比例；在A型或X型的基本图形中，寻找线段间的比例关系.

方法1：寻找子母三角形，根据相似三角形对应边成比例建立等量关系.

由结论①和结论②得△CGE∽△CBG，得到 CG2=BC·CE，由结论③和结论④得CF=CG，第（1）问中已经求得CF=BE，等量代换得到BE 2=BC·CE.

方法2：构造平行线，依据A型或X型的基本图形构造比例关系.

解法1：如图4，延长DC，AE交于点N. 由CD∥AB，得=，==，得CF=CN=BE，即得到=，即BE 2=BC·CE.

解法2：如图5，过点M作MN∥BC交AE于N，由MN∥BC，M为AB中点，得BE=2MN. 由MN∥BC，CF∥AB，得==，即=，BE 2=BC·CE.

3. 解图：积累基本模型，梳理基本方法

通过识图、研图的环节，虽然将一道题目顺利解决，但是如果就此画上句号，那么对部分学生而言还是停留在“就题论题”的层面，对于典型的例题，我们还需要做“加法”，进行追问：如何联想到寻找子母三角形？辅助线的添加还有其他情况吗？图中的哪些基本图形是解决问题的关键呢？正如著名数学教育家波利亚所说：“解题的价值不是答案本身，而是在于弄清‘怎样想到这个解法的，是什么促使你这样想、这样做的？”

问题（2）中BE 2=BC·CE中BE是BC和CE的比例中项，若从“相似三角形对应边成比例”思考，则BE应为子母三角形的公共边，而BE，BC，CE在一条直线上，因此寻找与BE相等的线段，将CG进行代换，利用△CGE∽△CBG，最终解决问题. 若从“平行线间对应线段成比例”思考，除了上述两种构造方法，有些学生还构造了图6的辅助线. 通过尝试，发现图6的三种辅助线都不能得到最终的结论，由于E是线段的分割点，M是线段的中点，故构造的基本图形必须同时涵盖这两个关键点. 图6的辅助线都只能得到相关的一组比例关系，因此无法得到最终的结论.

梳理整个解题过程，图7是例题中涉及的基本图形，而积累常见的基本图形和基本方法是将问题化繁为简的重要手段. 通过从复杂图形中剥离基本图形，可以将复杂问题变成一个个可以解决的小问题，通过串联小问题，达到解决问题的目的.

题组变式

题组变式是促进学生深度学习，提升学生高阶思维的有效方式. 瑞斯尼克深刻地指出：高阶思维具有不规则性和复杂性，能够产生多种解决方法，需要多种应用标准，学生能够自动调节，且包含不确定性. 而题组变式的目的就是通过对问题进行加工、补充、完善，使问题更具灵活性，从而提升学生的思维品质，培养学生的高阶思维.

1. 对调条件和结论

变式1  如图2，已知正方形ABCD，点M是边AB的中点，连结CM. 若在边BC上取一点E，满足BE 2=BC·CE，连结AE交CM于点G，交DC延长线于点N，连结BG并延长交边CD于点F.

求证：∠AGB=90°.

解法分析：尽管题目的结论和条件发生改变，但是问题的解决路径还是一致的，问题的突破点还是在于如何转化“BE 2=BC·CE”. 由于“∠AGB=90°”由已知条件变为所求结论，故寻找子母三角形的方法就行不通了. 但是构造平行线，利用比例线段求解的方法还是可行的，通过比例关系得到BE=CF，再证明△ABE≌△BCF（SAS），得到∠A=∠CBG ，最终求得∠AGB=90°. 这样的解题过程在潜移默化中培养了学生的逆向思维.

2. 改变考查形式

变式2  如图2，已知正方形ABCD，点M是边AB的中点，连结CM. 若在边BC上取一点E，满足BE 2=BC·CE，连结AE交CM于点G，交DC延长线于点N，连结BG并延长交边CD于点F.

求：tan∠CBF的值.

解法分析：由于題目中未出现线段的长度或明显的数量关系，故对求具体的三角比产生了不小的难度. 由“BE 2=BC·CE”，得E是BC的黄金分割点，=通过变式1的探索得到BE=CF，继而得到tan∠CBF==. 黄金分割比的融入在一定程度上体现了知识点的糅合，培养了学生的发散思维.

3. 改变元素关联

变式3  如图8，已知正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD，BC于点E，F，作BH⊥AF，垂足为H，BH的延长线分别交AC，CD于点G，P.

求证：（1）AE=BG；（2）GO·AG=CG·AO.

解法分析：本题是一个新的背景，但是可以发现的是图形中还是存在着子母三角形、X型基本图形. 在第（1）问中，解决方法还是围绕着利用全等三角形证明线段相等；在（2）问中，解决方法还是通过利用相似三角形、平行线间的比例线段证明线段间的比例关系. 不仅如此，本题还可以利用tan∠OBG=tan∠CBP来解决，由此产生了全新的解题思路. 这无疑提升了学生的类比、联想能力，拓展了学生的思维宽度.

以上三道问题通过从不同的角度进行变式，提升了学生不同维度的思维能力. 对题组进行变式，也是学生对知识再发现、再创造、再认识的过程. 在分析例题时，教师已充分挖掘题目内涵、总结通识通法、积累基本模型，这样做“加法”的过程帮助学生建构了系统化的知识网络，发展了深度化的高阶思维. 因此，当学生再遇到类似问题时，只需要做“减法”，剔除多余线段，抽象基本图形，利用相关结论，化未知为已知，问题便可解决.

教学建议

1. 应倡导“以题会类”而非“以题见类”

教师若采用“就题论题”的传统练习题教学模式，缺乏对知识本质的挖掘和方法的归纳，则只能起到“蜻蜓点水”之效. 虽然学生见识了多种类型，但遇到具体问题时该如何处理，恐怕只能取决于学生的自悟能力或平时量的积累所形成的“条件反射”. 因此，学生在面对复杂的几何证明时，往往显得手忙脚乱. 其实，若教师对每类问题逐一举例剖析，并适当地进行题组变式，则一定能把培养学生“以题会类”的迁移能力落到实处.

2. 应强调“基本方法”而非“剑走偏锋”

相对于代数问题，学生认为几何问题更难把控，一旦没有思路，整道题就只能被束之高阁了. 其实几何题的难度很大程度上由图形的复杂程度决定，而一个复杂的几何图形往往由多个基本图形组合而成. 如果学生已熟练掌握基本图形，他们在解题时就能对复杂问题进行拆分，做到化繁为简. 在几何教学时，教师只有引导学生积累基本图形、基本解决方法，注重题组变式，才能帮助学生实现从量变到质变的飞跃.

3. 应突出“学法指导”而非“实战演练”

解题方法是教学内容的精髓，是数学教学的灵魂，它渗透于数学教学的各个环节及问题解答过程. 专题复习的意义不在于检测学生的课堂解题能力，而在于解题方法的传授与思维方式的完善，着力点是引导学生学会“怎样转化”和“如何类化”. 因此，借助“目标分析”和“知识溯源”把思路生成的随机性转化为分析的必然性，妙用“本题属于什么类型”和“同一类型还可以怎么做”来引导学生进行迁移性的深度思考，必然能完善学生的思维方式. 由此可见，学生只有在题组分解、变换时做“加法”，才能最终在解决问题时做“减法”，从而全面提升分析问题能力，发展数学高阶思维.