可移动周期性维护排序问题的算法研究

华荣伟，潘虹，严甜海

（1.杭州医学院，浙江 杭州 310053；2.浙江大学 数学科学学院，浙江 杭州 310058）

0 引言

在实际生产中，可能因机器发生故障在一段时间内不能加工工件，也可能因预防性检修暂时停止加工，这就引出了在机器维护时段的排序问题。对机器在维护时段的排序问题研究始于20 世纪80 年代［1-2］，相关模型和结果可参考综述文献［3-5］。根据工件在加工过程中因机器维护被打断后的不同处理方式，分为三类［4］：（1）维护时段结束后，已经完成的部分作废，需重新加工该工件，称不可恢复（nonresumable）；（2）维护时段结束后，只需继续加工该工件尚未完成的部分，称可恢复（resumable）；（3）维护时段结束后，除继续加工该工件尚未完成的部分，还需处理已完成的部分，称半可恢复（semiresumable）。下文若不特别说明，所涉及的均为不可恢复问题。根据机器维护时段是否具有规律性，分为周期性维护（periodic maintenance）和非周期性维护。在周期性维护中，同一台机器两个相邻的维护时段之间具有某种规律。目前已有研究的模型大致可分为三类：相邻维护时段之间间隔恰为T，称为不可移动［6］；相邻维护时段之间间隔不超过T，称为可移动［7］；相邻维护时段之间间隔不小于-T，不超过-T，称为双向可移动［8］。一般假定维护时长t 为一固定值。对非周期性维护问题，一般均假设每台机器至多只有一个维护时段，否则很可能不存在最坏情况比为常数的近似算法［9］。因此，对有多个维护时段的周期性维护问题研究更困难，研究成果也相对较少。对于单台机、目标为极小化工件最大完工时间（makespan）、不可移动周期性维护问题，JI 等［6］证明了当时，除非P=NP，否则不存在最坏情况比小于2 的多项式时间近似算法，而最长加工时间优先（longest processing time，LPT）算法的最坏情况比恰为2。YU 等［10］以最优解所含维护次数为参数，给出了多个算法的参数最坏情况比。对单台机、目标为极小化总完工时间、可移动周期性维护问题，QI 等［7］证明了当t ＞T 时，问题是强NP-难的。QI［11］证明了最短加工时间优先（shortest processing time，SPT）算法的最坏情况比至少为，至多为。若目标为极小化工件最大完工时间、维护时段为双向可移动，XU 等［12］证明了不存在最坏情况比小于2 的多项式时间近似算法。CHEN［8］给出了最坏情况比恰为2 的算法。

平行机周期性维护排序问题以两台同型机、目标为极小化工件最大完工时间为主。对只有一台机器需要周期性维护且不可移动、另一台机器可持续加工的问题，XU 等［13］证明了列表排序（list scheduling，LS）算法和LPT 算法的最坏情况比分别为2 和。LI 等［14］给出了最坏情况比为的算法。对该问题的可恢复情形，同样存在最坏情况比为的算法。当两台机器均需周期性维护时，若维护时段不可移动，SUN 等［15］给出了最坏情况比为的算法。若维护时段双向可移动，XU 等［16］给出了最坏情况比为的算法，并证明了若P ≠NP，则不存在最坏情况比小于2 的多项式时间算法。对两台同型机，维护时段可移动、目标为极小化总完工时间的问题，SUN 等［15］给出了最坏情况比为的算法。LIU 等［17］分别研究了m台同型机和两台同类机的排序问题，其中一台机器存在不可移动周期性维护时段，其他机器均可持续加工，目标为极小化工件最大完工时间，给出了该问题相应的算法和最坏情况比。

1 可移动周期性维护排序问题

1.1 可移动周期性维护排序问题介绍

主要研究两台同型机需周期性维护且维护时段可移动、工件不可恢复、目标为极小化工件最大完工时间的排序问题。具体地，在两台机器M1，M2上分别安排n 个工件J={J1，J2，…，Jn}进行加工，工件Jj的加工时长为pj。每台机器连续加工时长不超过T后需进行一次时长为t 的维护，记。称每台机器上每个工件的连续加工时段为加工区间，k=1，2，…，共有k 个加工区间，如图1 所示。本文将给出算法的参数形式的最坏情况比。

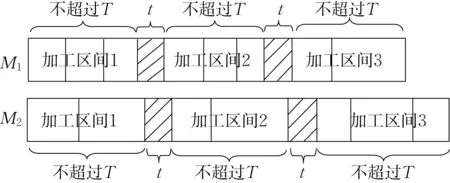
图1 需周期性维护且维护时段可移动的两台同型机Fig.1 The two parallel machines with flexible periodic maintenance activities

1.2 装箱问题与FFD 算法

可移动周期性维护排序问题与装箱问题类似。装箱问题（bin-packing）［18］描述如下：

有一组物品L={a1，a2，…，an}，物品ai的大小s(ai)∈(0，T]，需将这些物品装入容量为T 的箱子，问至少需要启用几只箱子？装箱问题也是NP-难的，本文主要涉及装箱问题的按物品大小递减的最先用（first fit decreasing，FFD）算法。

对物品重新排序：s(a1)≥s(a2)≥…≥s(an)。将物品ai（i=1，2，…，n）依次装入能容纳序号最小的箱子。具体地，如果已经启用的箱子中存在能容纳ai的箱子，则将ai放入满足此性质的序号最小的箱子，如果不存在，则将ai放入未启用的序号最小的箱子。

其中，Bi表示第i 个启用的箱子，也表示放入第i 个箱子中物品的集合，S(Bi)为装入该箱子中物品的大小之和。

引理2 若，则，…，Bb中的物品大小均不超过。

引理2 给出了FFD 算法的基本性质，证明见文献［18］。

由引理2，可对物品之和的大小做估计。

证明（i）由FFD 算法，可知对任意的1 ≤i ＜j ≤b，有S(Bi)+S(Bj)＞T，进而有

由S(Bb-1)+S(Bb)＞T，可知

证毕！

1.3 P2||Cmax 及完全多项式时间近似方案（FPTAS）

算法将调用P2||Cmax问题的近似方案，P2||Cmax即两台同型机、机器不用维护、目标为极小化工件最大完工时间。SAHNI［20］给出了该问题完全多项式时间的近似方案（FPTAS），其最坏情况比为1+ε，时间复杂度为实例规模与的二元多项式函数，其中ε为任意小的正数。

1.4 符号说明

用Cmax(σ)表示排序σ 的最大完工时间，Li(σ)表示在机器Mi上工件的最大完工时间，Pi(σ)表示在Mi上工件的总加工时间，也称Mi的负载。用bi(σ)表示在Mi上的加工区间数，Ji，k(σ)表示在Mi上第k个加工区间内加工的工件集。对任意工件集S，用P(S)表示工件集S 中工件的总加工时间。用CH表示算法H 给出的排序的目标值，C*为最优值。

2 算法的难近似性

定理1若两台机器中的任一台每连续加工时长至多为T 后需进行一次时长为t 的维护，则不存在最坏情况比小于1+β 的多项式时间近似算法，除非P=NP。

证明反证法。假设存在多项式时间近似算法A，其最坏情况比为α ＜1+β。用NP-完全的划分问题［21］进行归约，划分问题可描述为：给定n 个正整数e1，e2，…，en，满足，是否存在子集X ⊆S，使得。

给定划分问题的一个实例I，按照下述方法构造原问题的实例I'。

令T=B，t=βB，有两台机器和n 个工件，其中工件Ji的加工时间为pi=ei(i=1，2，…，n)，显然可以在多项式时间内完成归约。若实例I 的答案为存在，则令J1(σ)={Ji|ei∈X}，J2(σ)={Ji|ei∈SX}，可得最大完工时间为T 的排序，故实例I'的最优最大完工时间C*≤T。

对实例I'，由算法A 得到的排序为σA，最大完工时间为CA。不妨假设σA满足性质：

如果对于某台机器Mi，bi(σA)＞1，则

若不然，可通过合并加工时段满足该性质，使上述步骤在多项式时间内完成且目标值不增加。

如果CA≤T，则有Li(σA)≤T。由

如果CA＞T，不妨假设L1(σA)＞T。显然可得P1(σA)≥P1(J1，1(σA))+P2(J1，2(σA))，b1(σA)≥2。因此L1(σA)＞t+T。由最坏情况比的定义，可知

因此划分问题实例I 的答案是不存在。

至此，得到了划分问题的多项式时间算法，这与划分问题是NP-完全的矛盾。

证毕！

3 算法和最坏情况比分析

3.1 算 法

由定理1 可知，若不将算法的最坏情况比表示为β 的函数，当β 为非固定数时，任意算法的最坏情况比均不是有限常数。

下面给出一种近似算法H，其最坏情况比为β的一个分段函数。

3.1.1 子过程Greedy

设在当前排序中，机器Mi的完工时间为Li，Mi有bi个加工区间，在第k 个加工区间内加工的工件子集为Ji，k，k=1，2，…，bi，i=1，2。当前工件子集为Bj：

（i）对i=1，2，记li为可以在Mi上加工的最早加工区间序号，为Bj在Mi上加工Mi的最早完工时间。具体地，如果存在k ≤bi，使得P(Bj)+P(Ji，k)≤T，则令

若这样的k 不存在，则令li=bi+1，

3.1.2 算法H

运用复合思想，当工件总加工时间较短时，调用P2||Cmax的FPTAS；当工件总加工时间较长时，先分批，然后将各批作为一个整体在某个加工区间内加工。

（i）将工件加工时间视为物品的大小，T 为箱子容量，构造装箱问题实例，并用FFD 算法进行分批。记所得批数为 b，各批工件子集为B1，B2，…，Bb-1，Bb，不妨设P(B1)≥P(B2)≥…≥P(Bb)。

（ii）若P ≤2T，调用P2||Cmax的FPTAS，若在其中一台机器上工件总加工时间大于T，则在该机器上增加一个维护时段，以使在维护时段前后加工的工件总加工时间不超过T。

（iii）若 P ＞2T，则对子集族{Bi} (i=1，2，…，b) 应用子过程Greedy。

3.2 最坏情况比

下面给出算法H 的最坏情况比的上界。将算法得到的排序记为σ，先给出几个引理。

引理4若P ＜2T，则。

证明考虑工件集为J 的两台无维护时段同型机排序问题，记用FPTAS 求解该实例所得的排序为σF，最优排序为σ'。由FPTAS 的定义，可知Cmax(σF)≤(1+ε)Cmax(σ')。注意到有维护时段问题的最优值不小于无维护时段问题的最优值，即Cmax(σ')≤C*。

若在σF中，两台机器的负载均不超过T，则两台机器均不需要引入维护时段，因此

反之，假设至少有一台机器负载大于T，注意到P ≤2T，至多有一台机器负载超过T，不妨假设为机器M1。此时在机器M1上需要增加一个维护时段，因此CH≤Cmax(σF)+t。如果C*≤(1-ε)T，则

这与σF中M1的负载大于T 矛盾，所以C*＞(1-ε)T。此时

证毕！

引理5（i）记b*=b1(σ*)+b2(σ*)，则最优排序；

（ii）若b*≥3，则。

证明（i）显然成立。

（ii）若b*≥4，由（i）可知（ii）成立。若b*=3，则在σ*中完工时间较长的机器上，不妨假设为M1，必有一个维护时段。若不然，则，显然有

这与M1完工时间较长矛盾。因此，必有b1(σ*)=2且b2(σ*)=1。显然可得P1(σ*)＞T ≥P2(σ*)，否则，M1不需要维护。因此

证毕！

记

由于ε 可任意接近于0，定义

显然f0(β)≤f (β)，且f0(β)与f (β)可任意接近。图2 为函数f0(β)的图，可得f (β)的性质：

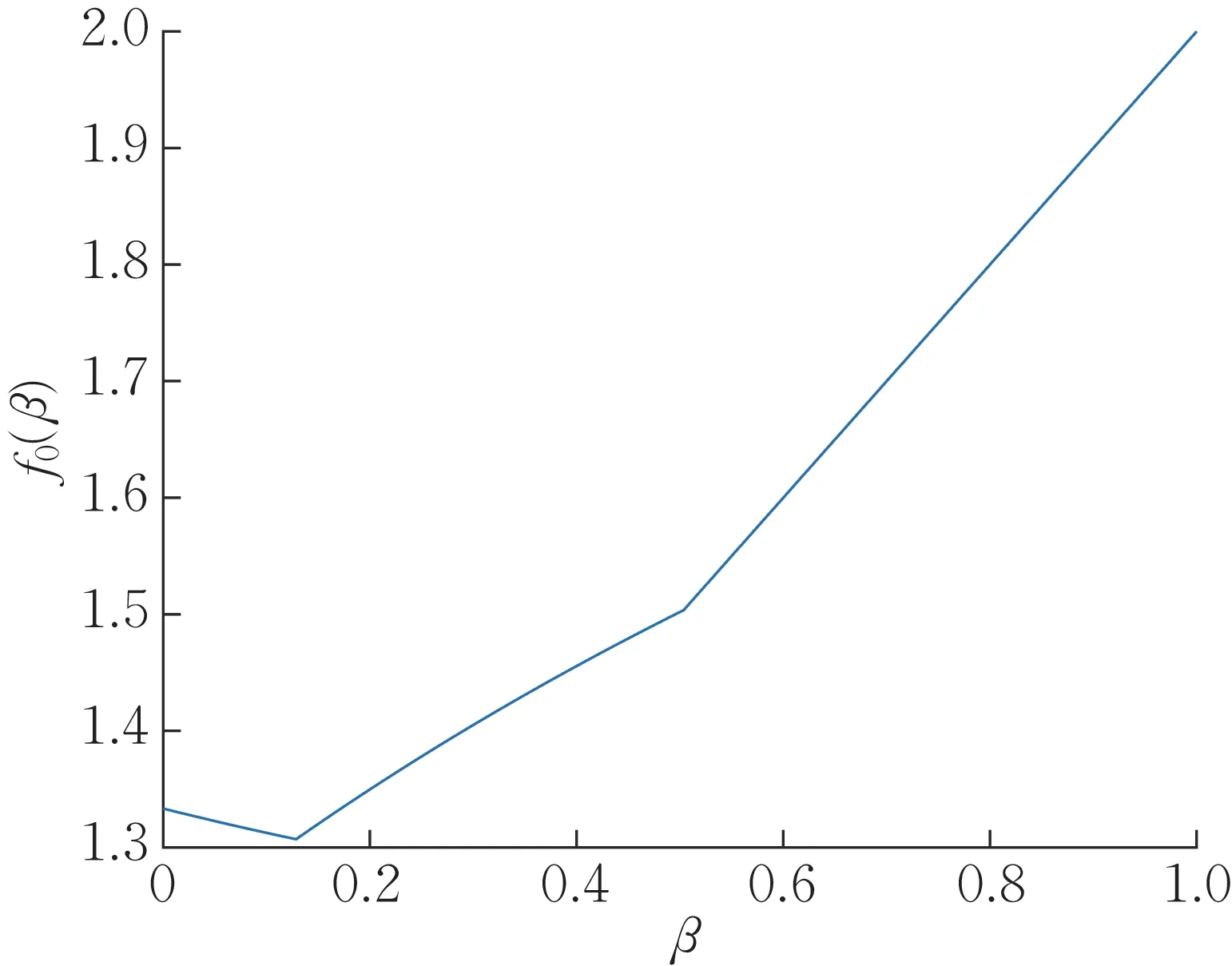
图2 函数f0(β)的图Fig.2 The function image of f0(β)

证毕！

定理2若两台机器均需周期性维护，每台机器连续加工时长至多为T 后需进行一次时长为t 的维护，算法H 的最坏情况比不超过f (β)，其中，β=。

证明根据P 的大小分情况讨论。

若P ＞2T，则b*≥≥3。

若b=3，子过程Greedy 必将B1安排在M1上加工，将B2和B3安排在M2上加工。因此，

由引理5（ii）和P ≥3P(B3)，有

如果B4批决定最大完工时间，则有

由L1(σ)+L2(σ)=P+(b-2)t=P+2t，有

由引理5（ii）、式（1）和P ≥4P(B4)，有

如果B3批为决定最大完工时间，类似地可得

由引理5（ii）、式（2）和P ≥3P(B3)，有

综上，在该情形下，由引理6（i），可得

若b ≥5 且Bb决定最大完工时间，不妨假设CH=L1(σ)。由Greedy 规则，可得

由L1(σ)+L2(σ)=P+(b-2)t，可得

由引理5（i）和P ≥bP(Bb)，有

其中，最后一个不等式由b ≥5 得到。

由引理6（ii），若b ≥5 且由最后一批决定最大完工时间，则有

若b ≥5 且Bb批不决定最大完工时间，则σ 中Bb-1批一定是决定最大完工时间的。若不然，假设σ 中L1(σ)＜L2(σ)，将Bb，Bb-1，…，Bl同时安排在M1上、Bl-1安排在M2上加工，其中l ≤b-1。假设在安排Bl-1时，Mi的完工时间为L'i(i=1，2)，则

而由FFD 算法规则，可知

这与Bl-1批被安排在M2上加工矛盾。

考虑以J{Bb}为工件集的实例I'，用FFD 算法对J{Bb}进行分批，所得工件子集恰为B1，B2，…，Bb-1。对实例I'，注意到此时b-1 ≥4，运用算法H所得排序σ'的最大完工时间与实例I 的排序σ 的最大完工时间相同，且σ'中Bb-1批决定最大完工时间，而C*(I')≤C*(I)，因此，由式（3）或式（5），有

证毕！

4 结论

对于可移动周期性维护排序问题，证明了其不存在最坏情况比小于的多项式时间近似算法，除非P=NP，同时给出了该问题的近似算法，证明了其最坏情况比不超过。