两道高三模拟试题的命题手法剖析
何 灯 叶诚理
(福建省福清第三中学 350315) (福建省福清第一中学 350300)
网传,数学解题有五重境界,从低阶到高阶分别是:正确解题、一题多解、多题一解、发现定理、自己编题.诚然,不是所有的人都具备编题的能力,但是,钻研他人命制的试题,探究其命题规律,遵循规律进行试题的再命制,不失为快速提升自身审题、解题、变题、教题、说题、命题能力的一个行之有效的途径.
受到文[1]启发,本文探究近期出现的两道高三质检试题,先从解法出发探究试题的命题规律,再借助此手法,实现试题的再命制.笔者只是旁观成题,对命题者命题过程作了思考、揣测、推演、模仿,可能并非命题者的真正命题意图,因而文中所述仅供读者参考.
1 试题解法分析
题1(福建省部分学校2022—2023学年高三12月大联考第22题)已知函数f(x)=x2e2x.
(1)求函数f(x)的极值;
(2)若关于x的不等式f(x)≥2ax+2lnx+1恒成立,求实数a的取值范围.



(1)若a<0,讨论f(x)的单调性;

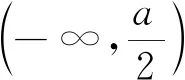

评析上述两道试题中问题(2)的求解,均是将恒成立的不等式等价变形为含p(x)- lnp(x)的形式,再借助不等式p(x)- lnp(x)-1≥0,将不等式恒成立这一条件转化为含参数a的一个不等关系,最终求得参数a的取值范围.
2 命题思路剖析
通过上述两道试题求解的逆向推演,不难管窥命题者的命题手法.笔者将其整理为如下5个步骤.
步骤一(选取不等式模型) 选择一个较为简洁的含ex或lnx的不等式,使其能够取等成立(如:x-1-lnx≥0,x-elnx≥0,ex-1-x≥0,ex-ex≥0等).题1和题2选取的不等式模型是x-1-lnx≥0.
步骤二(确定代换函数模型) 在步骤一的基础上,将不等式中的变量x替换为某个函数模型(若步骤一中选取的是含ex的不等式,则可以尝试选取xm±lnxn,a(xm±lnxn)等;若步骤一中选取的是含lnx的不等式,则可以尝试选取xmenx,axmenx(a>0)等),记得到的不等式为F(x)≥0.题1中选取的代换函数模型是x2e2x,得到F(x)=x2e2x-ln(x2e2x)-1;题2中选取的代换函数模型是axex,得到F(x)=axex-ln(axex)-1.


步骤五(进行合理设问) 为了体现题目的梯度,让不同层次的学生都能充分发挥出自己的水平,试题的第一问应当尽量浅显(可以讨论函数f(x)的单调性、极值、最值、切线等,同时为第二问的解答提供台阶,埋下伏笔).第二问研究关于x的不等式f(x)≥f(x)+G(x)-F(x)(或取“>”)或f(x)≤f(x)+F(x)-G(x)(或取“<”)恒成立,求参数a的取值范围.题1中问题(1)研究f(x)的极值,同时其单调性的确定为问题(2)的求解埋下伏笔,问题(2)研究不等式f(x)≥f(x)+G(x)-F(x)(即F(x)≥G(x))恒成立,求参数a的取值范围.题2中问题(1)研究f(x)的单调性,问题(2)研究不等式f(x)
3 新题命制赏析
本环节,笔者遵循上述五个步骤,尝试命制两道相关试题,以使读者对该类试题的命题流程获得更深入的理解.
命题1步骤一(选取不等式模型) 选取x-elnx≥0.
命题1步骤二(确定代换函数模型) 将x-elnx≥0中的x替换为axe2x,得到axe2x-eln(axe2x)≥0,令F(x)=axe2x-eln(axe2x)=axe2x-eln(ax)-2ex.
命题1步骤三(构造含参函数模型) 选取G(x)=(a-2e)x.
命题1步骤四(选定题设函数模型) 将不等式axe2x-eln(ax)-2ex≥(a-2e)x化简, 得到xe2xa-eln(ax)≥ax,取f(x)=ax-eln(ax).
命题1步骤五(进行合理设问) 为了渗透分类与整合的数学思想,同时给问题(2)的求解埋下伏笔,笔者意图将不等式x-elnx≥0内含到问题(1)中,故设定问题(1)为:讨论函数f(x)的单调性.由f(x)≥f(x)+G(x)-F(x),得f(x)≥ax(2-e2x),故设定问题(2)为:若 ∀x∈(0,+∞),f(x)≥ax(2-e2x),求实数a的取值范围.
综合上述命制过程,得到如下新题.
题3已知函数f(x)=ax-eln(ax).
(1)讨论函数f(x)的单调性;
(2)若∀x∈(0,+∞),f(x)≥ax(2-e2x),求实数a的取值范围.
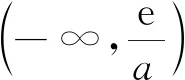
命题2步骤一(选取不等式模型) 选取ex-1-x≥0.
命题2步骤二(确定代换函数模型) 将ex-1-x≥0中的x替换为2x+lnx,得到e2x+ln x-1-2x-lnx≥0,令F(x)=e2x+ln x-1-2x- lnx=xe2x-1-2x-lnx.
命题2步骤三(构造含参函数模型) 选取G(x)=(a-2)x.
命题2步骤四(选定题设函数模型) 将不等式xe2x-1-2x-lnx>(a-2)x化简,得到xe2x-ax-lnx-1>0,取f(x)=ax-lnx+1.
命题2步骤五(进行合理设问) 笔者意图将不等式x-lnx-1≥0内含到问题(1)中,故设定问题(1)为:求函数f(x)的极值.由f(x) 综合上述过程,得到如下新题. 题4已知函数f(x)=ax-lnx+1. (1)求函数f(x)的极值; (2)若关于x的不等式f(x) 限于篇幅,题3和题4的详细求解过程此处从略,有兴趣的读者可自行研究. 本文通过深耕两道试题,开启了一段试题命制探究之旅,将试卷上“冰冷的美丽”转化为“火热的思考”.这种基于探究策略的试题研究,对数学教师专业素养的提升有极大的裨益.同时,学生通过对试题的研磨,经历对各种解答策略的比较、各类函数模型之间的结构与关系的抽象、各数值之间的分析与比较、算理与算法的甄别、数学软件与多媒体的动态演示等,有助于形成理性思维,树立科学精神与态度,从而促进智力发展,发展核心素养.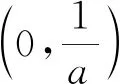
4 思考与感悟

