求流模型下带比率的集函数最大值问题求解研究*

耿红梅

（扬州工业职业技术学院）

0 引言

近几十年来，数据以流模型的方式传输的情况受到了大量的关注.在提取海量数据信息的过程中，出现了受基数约束的非次模集函数最大化问题［1］.然而，事实上，对于非次模函数的最大值，要想求解其精确值是非常困难的，很难在多项式时间内得到它的精确解.但是这些非次模优化问题的广泛应用又使其求解成为必须［2］.因此，往往通过牺牲精度来换取时间，即在多项式时间内得到问题的一个近似解，这便是近似算法［3］.在流模型下，如果收益函数是次模函数，则称该模型为流次模函数最大化问题.对于流次模优化的问题，Badanidiyuru［4］引入衡量其算法性能的4 个指标，分别为：（1）数据流被读取（访问）的次数；（2）空间复杂性，指存储数据的规模；（3）运行时间，一般指计函数值的调用（查询）次数；（4）近似比，指流结束时算法输出解的值与当前流下最优值的比［4］.与传统离线模型的近似算法相比，流算法更加注重存储空间的有效性，学者们提出许多适用于流模型次模最大化问题的算法，比如基数约束流次模最大化问题［5］、背包约束流次模最大化问题［6］、独立系统约束的流次模最大化问题、带滑动窗口的次模最大化问题和在线次模最大化问题等［7］.对于大规模流数据的次模优化问题，由于之前的次模优化算法需要反复访问完整的数据集，人们不能将它们直接应用于海量流数据，因此Badanidiyuru团队在《Streaming submodular maximization：massive data summarization on the fly》一文中提出了一种求解在基数约束下的次模极大化问题的有效方法.在大规模机器学习应用中，除了流算法，还有其他一些关于次模集函数最大化的算法，包括在线算法、随机贪婪算法、分散式演算法等［8］.该文主要通过构造一个满足流模型下条件的带比率集函数，改进之前已有的算法，并进行分析和证明，以获得相应的近似比，更快速更精确地解决在提取海量流数据信息的过程中出现的受基数约束的非次模集函数最大化问题.

1 相关理论概述

1.1 问题提出

1.2 基本定义

定义1［9］（多项式时间算法）称一个算法是多项式时间可解的，如果该算法对于问题输入占有空间大小为n的时间复杂度为O（nk），其中k是一个非负整数.

定义2［9］（P类）所有可以用确定型图灵机在多项式时间内求解的判定问题.

定义3［9］（NP 类）所有可以用非确定型图灵机在多项式时间内接受的判定问题实例.

定义4［9］（近似比）一个α－近似算法A定义如下：对于实例x，可以证明算法A的近似解A（x）的值不会比最优值OPT的α倍更多（或更少，这取决于具体问题）.

系数α称为算法A的近似比.

定义5［10］（次模函数）如果对于任意子集X，Y ⊆G，有f（X）＋f（Y）≥f（X ∩Y）＋f（X ∪Y），则称集合函数f是次模函数.

定义6［10］（边际增益）对于任意e ∈G和S ⊆G，△f（e，S）＝f（e ｜S）＝f（S ∪｛e｝）－f（S）表示数据e加到集合S中产生的边际增益.

定义7［10］（单调性）如果对于任意S ⊆T ⊆G，都有f（S）≤f（T），则称集合函数f单调不减.

定义8［10］（归一化）如果f（∅）＝0，则称集合函数f是归一化的.

定义9［10］（次模最大化）一般来说，次模函数的最大化问题可以定义为：

其中集合函数f：2G→R ≥0在具有基数约束的子集S上，即｜S ｜≤k.

定义10［13］（非次模）非次模集函数f 的定义：对于任意S ⊆T，e ∉T，γ ∈［0，1］有

2 算法设计

该文改进了在流模型下满足基数约束的求解非次模函数最大化问题的3种算法.算法的主要思想是提前设置一个阈值，这些算法的结果从一个空集开始，即S ＝∅，如果新元素同时满足阈值条件和基数约束，就将其添加到解集S中.

2.1 已知最优值的算法

在经典的次模极大化贪婪算法中，会在每次迭代中选择具有高边际值的元素，但是在流模型中决定当前元素是否具有足够的边际增益是一个挑战.一般的想法是以某种方式将其与最优值OPT进行比较.如果能够知道所有的数据信息，就可以利用二分法找到最优值.但在流模型中，要找到最优值并不容易，因此，在该文中假设了OPT为式（1）的最佳值.此外，还需要设置一个直观的值来模拟满足αOPT ≤v ≤OPT 的最优值，其中α ∈［0，1］.将递减收益率γ与v相结合，改进了之前已有算法的系数，重新构造一个特定的阈来计算新的来源元素.

算法1给定一个基集G，令n ＝｜G ｜，整数k ≤n，一个集合函数f，f 的递减收益率为γ ∈［0，1］，参数α ∈［0，1］，实数v∈［αOPT，OPT］，令S ∶＝∅，i ∶＝1.

步骤2如果i ＝n，输出S；否则，令i ∶＝i ＋1，再回到步骤1.

传递次数、存储元素的内存和每个元素的更新时间（读取新元素时的oracle调用次数）可以通过以下引理来估计.

引理1只扫描一次数据流，存储最多k 个元素，每个元素有O（1）更新时间.

为了分析算法的性能保证，提出以下技术引理来判断子集S 在每一个循环中的平均质量水平.

引理2在子集为S 的算法的每一个循环中，有

证明可以通过数学归纳法来证明式（2）.

定理1对于任意给定的实数α ∈［0，1］和具有递减收益率γ ∈［0，1］的非次模函数f，算法产生一个集合S，使得｜ S ｜≤k，且f（S）≥，其中OPT是式（1）的最优值.

证明考虑以下关于约束算法输出的解集S的基数的2种情况.

2.2 已知最大单例值的算法

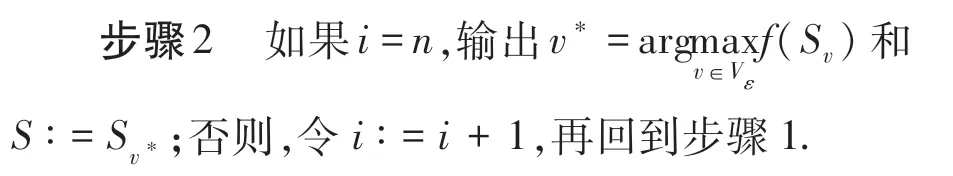
引理3算法扫描数据流两次，最多存储O（klog（k／γ）／ε）个元素，每个元素的更新时间为O（log（k／γ）／ε）.

下面的引理表明最优值候选集包含一个接近真正最优值的值.

引理4存在一个值v ∈Vε，使得（1－ε）OPT ≤v ≤OPT.

定理2算法对于任意0 ＜ε ＜1，0 ≤γ ≤1输出解集S，使得｜S ｜≤k，且有f（S）≥

证明同样考虑两种情况.

2.3 更新近似最优值候选集的算法

算法3给定一个基集G，令n ＝｜G ｜，整数k ≤n，一个带有递减收率γ ∈［0，1］的集合函数f，设m：＝0，i：＝1，V0：＝∅，V：＝｛（1 ＋ε）l｜l ∈Z｝.对于每一个v ∈V，设Sv：＝∅.

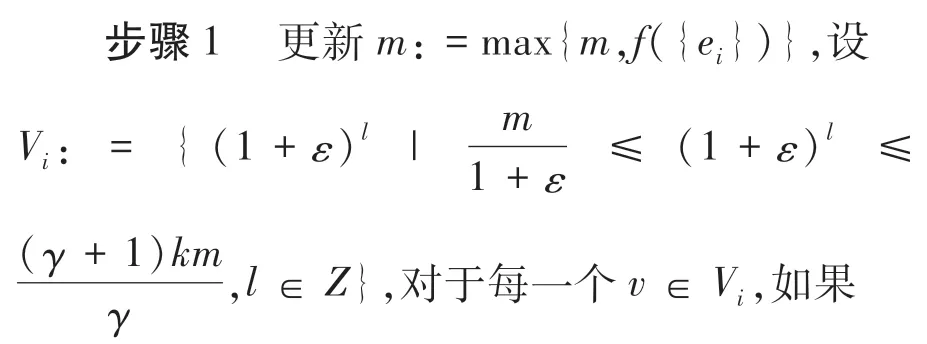
其中｜Sv｜＜k，则设Sv∶＝Sv∪｛ei｝，删除所有Sv，使v ∈Vi－1＼Vi.

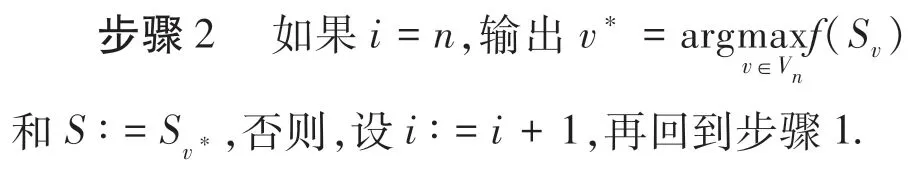
引理5［2］算法只扫描一次数据流，最多存储O（klog（k／γ）／ε）个元素，每个元素有O（log（k／γ）／ε）更新时间.

下面的引理6表明了阈值在i（v）之前不满足.因此，可以假设从一开始就检查每一个v.

引理7对于任意ε ∈（0，1），算法产生了满的解集S，其中γ是f的递减收益率.

3 结论

该文研究了流模型下受基数约束的非次模集函数的最大化问题，主要改进了三种利用递减收益率的算法.算法1 只扫描一次数据流.存储元素的内存为k，每个元素的更新时间为O（1），近似比为，其中α ∈［0，1］为参数，γ ∈［0，1］为集合函数的递减收益率.算法1 要求知道最优值，但实际上这通常是不可能的，而算法2构造了一组数字，其中至少有一个数字接近最优值.为此，算法2 必须扫描数据流两次并存储O（klog（k／γ）／ε）个元素.算法2 的近似比为，每个元素的更新时间为O（log（k／γ）／ε）.在算法3中，当每次扫描数据流中的新元素时，就会更新近似最优值的候选集.因此，它只需要扫描一次数据流就可以保持相同的近似比率、储存元素的内存以及算法2中每个元素的更新时间.其实，除了利用递减收益率，还有一些其他方法也可以用来研究非次模函数，比如次模比和曲率.现有工作中关于次模最大化的研究有很多，但是对于非次模最大化的问题有待更加深入的研究和探讨.