巧用源于教材的变式拓展 提升学生素养

武威第八中学 徐殿雄

数学教学离不开解题,掌握数学就意味着要善于解题.解题不仅仅是单纯的解答或推证出结果,更重要的是如何探源溯流,找寻试题结论的本质,挖掘试题背后蕴藏的思想,通过解题引发学生思考与交流,提升数学思维能力,形成和发展学生的数学学科核心素养.

1 从源头探究

例1求直线l1:3x+4y-2=0和l2:2x+y+2=0的交点坐标.

解析：l1和l2的交点为M(-2,2).过程略.

评注：这是人教A版普通高中数学选择性必修第一册第70页例1,基础题,主要考查两条直线的交点问题,考查学生的“数学运算”核心素养,其实质就是联立直线方程,求解方程组.

思考：交点为M(-2,2)的直线l1和l2唯一吗?,若不唯一,如何表示?

众生:不唯一.

师:我们把过该点的直线叫直线系,如何用方程来表示,请先看下面的探究.

拓广探究：已知λ为任意实数,当λ变化时,方程3x+4y-2+λ(2x+y+2)=0表示什么图形?图形有何特点?

分析1：令3x+4y-2=0且2x+y+2=0,则方程组的解是x=-2,y=2,即方程3x+4y-2+λ(2x+y+2)=0表示过点M(-2,2)的一族直线系.

分析2：令λ=0,1时,分别得到方程3x+4y-2=0和x+y=0,联立方程并解得x=-2,y=2,即方程3x+4y-2+λ(2x+y+2)=0表示经过点M(-2,2)的一族直线系.

变式不论λ为何值,直线(3+2λ)x+(4+λ)y-(2+2λ)=0都恒过定点.

在教学中从典例出发,适时改编设问方式换一副“新面孔”,有助于学生创新意识和创新精神的培养,在变式中抓住题源,似曾相识,更能充分调动学生的积极性,开阔视野,发展核心素养.这种含参直线恒过定点的问题在实际应用中较为广泛,如在圆锥曲线有关定点、定值问题中常常用到这种方法.

2 从特殊到一般拓展探究

例2已知直线l1:A1x+B1y+C1=0与直线l2:A2x+B2y+C2=0相交,证明方程A1x+B1y+C1+λ(A2x+B2y+C2)=0 (λ∈R)表示过l1与l2交点的直线.

证明：设P(x0,y0)是直线l1与l2的交点,则有A1x0+B1y0+C1=0且A2x0+B2y0+C2=0.于是A1x0+B1y0+C1+λ(A2x0+B2y0+C2)=0(λ∈R),所以D(x0,y0)也是直线A1x+B1y+C1+λ·(A2x+B2y+C2)=0(λ∈R)上的点.问题得证.

评注：本题涉及过两条相交直线交点的直线系方程如何写;反之,如何求出含参的直线系的交点坐标.特别地,若P(x0,y0)是两条互相垂直的直线l1与l2的交点,则过点P的直线系方程是y-y0=k(x-x0),即(y-y0)-k(x-x0)=0,应用十分广泛.

先从直线方程的特殊性(x,y的系数及常数项已知)到直线方程一般式(x,y的系数及常数项未知)的变式,再到用变化的观点去学习教材知识,抓住直线“变”与交点“不变”的核心,培养学生的创新意识.同时,这种变式的方法为发挥教材中习题的典型性、示范性提供了可借鉴的方法[1].

3 类比联想,拓展圆系方程探究

由直线系方程是否可以联想到圆系方程呢?回答是肯定的.把“两条直线相交”改为“两圆相交”,可以类比写出圆系方程,这样可获得同类知识的相关结论并灵活加以运用.

例3求圆心在直线x-y-4=0上,并且经过圆x2+y2+6x-4=0与圆x2+y2+6y-28=0的交点的圆的方程.

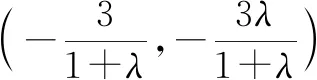
评注：解析2正是例2结论的推广,利用此结论解题能打破常规思维(如解析1),方法简便,过程简洁.

4 类比联想,拓展曲线系方程探究

除直线系方程和圆系方程外,我们大胆地联想还会有“椭圆系”“双曲线系”以及“抛物线系”方程,而这些方程可用“曲线系”方程代表.联想、类比获得同类知识的相关结论,能使学生在解题过程中体会、理解解决这类问题方法和区别所在,提高学生分析问题的能力.

例4已知曲线C1:f1(x,y)=0与C2:f2(x,y)=0相交,证明方程f1(x,y)+λf2(x,y)=0 (λ∈R)表示过C1与C2交点的曲线.

本题仿照例2容易得证,利用此结论易求教材第98页习题2.5的第7题:求经过M(2,-2)以及圆x2+y2-6x=0与x2+y2=4交点的圆的方程.

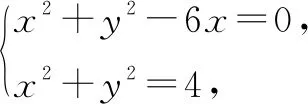
解法2：设所求圆的方程为x2+y2-6x+λ(x2+y2-4)=0.因为M(2,-2)在圆上,将它代入方程,得λ=1,所以所求圆的方程为x2+y2-3x-2=0.

评注：本题还可以设出圆的一般方程,将三点坐标代入求解.这两种解法比较,显然解法2简捷明了,精彩纷呈.解题的关键是正确设出圆的方程.这是过两条曲线交点的曲线系方程的标准形式,也给出了求该曲线恒过某一定点的方法.由易到难、由简单到复杂的变化,能使学生从变中发现数学题之间的联系与本质区别以及题目“难”与“易”的辩证关系.

5 直线与圆位置关系中的定点、定值问题

例5已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.

(1)求证:直线l恒过定点.(2)直线l被圆C截得的弦何时最长、何时最短?并求截得的弦长最短时m的值以及最短弦长.

(1)证明：直线l:(2m+1)x+(m+1)y-7m-4=0可化为x+y-4+m(2x+y-7)=0.

所以直线l恒过定点A(3,1).

(2)解：直线l被圆C截得的弦长最长时,直线l过圆心;直线l被圆C截得的弦长最短时,弦心距最大,此时CA⊥l.

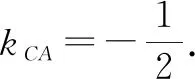
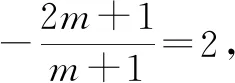
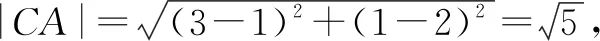
评注：本题考查直线恒过定点与弦长的计算问题.第(1)问利用例2的结论可以获解;第(2)利用圆的特殊性,明确过圆内定点的弦何时最长,又何时最短,然后利用弦心距、弦之半、半径构成直角三角形获解.

如果本题第(1)问证明“不论m为何值时,直线l和圆C恒有两个交点”,那么只需判断直线l恒过的定点在圆内即可,或联立直线和圆的方程,得到含参的关于x的一元二次方程,再用判别式即可判断.

6 高考真题再现及其结论的应用

我们发现教材基础题与高考选拔题确实有一定的差异,但不能因此抛开教材,而应更加熟练地掌握教材内容及其中蕴含的方法,这样才能从容应对“源于教材而高于教材”的高考题.

(1)求E的方程;

(2)证明:直线CD过定点.

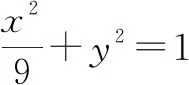
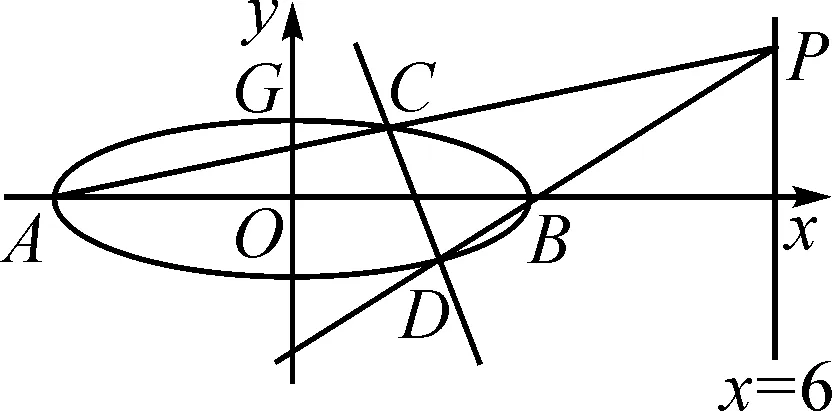
图1

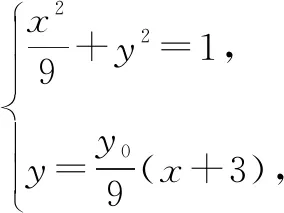
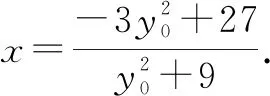
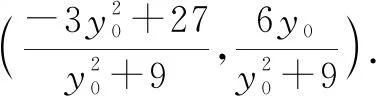
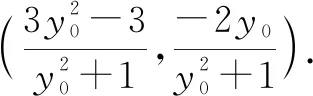
所以,直线CD的方程为

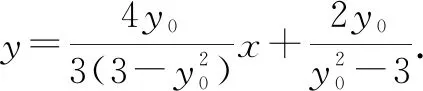
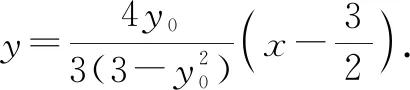
评注：本题第(1)问主要考查了椭圆的简单性质及方程思想.第(2)问欲证明直线CD过定点,首先要求出直线CD的方程,这个方程是用点P的纵坐标y0作为参变量表示的;其次,需要分别求出C,D两点的坐标,而C,D两点的坐标已知条件说得很清楚;最后,用直线方程的点斜式写出方程,化为y-y0=k(x-x0)的形式,即可说明直线恒过点(x0,y0).证明的目标很明确,需要转化思想和推理论证能力,对学生计算能力的要求较高.学生往往对含字母的运算望而生畏,心有余而力不足,导致证明半途而废.

7 结束语

挖掘教材知识、串联教材各考点的知识,根本目的在于让学生能够触类旁通、融会贯通,学会探索和研究,在交流探究过程中,培养分析问题和解决问题的综合品质.圆锥曲线中一个重要考点就是定点、定值问题,由于隐去题析增强了探索性,所以增加了试题的难度.因此,教师应引导学生打牢基础,教会学生能够把教材前后之间的知识点、考点、相互关联点交织成网,掌握解题过程中“动中求静,静中窥动”的思维特点.通过分析图形找定点、探索共性寻定点、巧赋值找定点、仔细观察猜定点等方法培养学生综合运用知识的能力.这类问题正因为探索性强[2],因而是发展学生创新思维、全面提升学生素质的好题材,教学中一定要充分利用其教学价值.