6轴工业机器人工作空间快速求解
李星辰,杨国庆,王宪,胡文洪
(湖南科技大学 机电工程学院,湖南湘潭 411100)
机器人工作空间是评价机器人工作性能的一项重要指标[1]。工作空间分为可达工作空间和灵巧工作空间。可达工作空间是指机器人末端执行器参考点所能到达的位置的集合,灵巧工作空间是指机器人末端执行器能以任意姿态到达的位置的集合[2]。实际上,由于机器人的几何属性和关节运功范围的限制,机器人的灵巧工作空间是不存在的[3]。在工程实际中,通常采用灵活工作空间代替灵巧工作空间[4]。
机器人工作空间是机器人设计与优化的重要依据。王晓华等以六轴缝纫机器人为对象,通过对机器人末端的可达工作空间分析确定了缝纫机器人在工作时各关节的最佳运动范围[5]。荆学东等以六轴双臂服务机器人为对象,求解了双臂各自的可达工作空间,以协作空间最大为优化目标,对机器人的结构参数进行了优化[6]。赵智远等研制了9自由度超冗余串联机械臂,以可达工作空间与灵活工作空间为优化目标,对机械臂的构型进行了优化设计[7]。贾世元等以六轴机械臂为对象,以全局灵活性为优化目标,对机械臂尺寸参数进行了优化设计[8]。
目前,求解机器人工作空间的方法主要有3类:几何法、解析法和数值法[9]。几何法可以得到机器人的解剖面或解剖线,但受到自由度数的限制,无法精确描述多自由度机器人的工作空间,主要用于平面机器人的求解[10]。解析法是通过多次包络求解机器人工作空间的方法,可以求出工作空间边界的数学方程,但求解过程复杂,主要用于关节数量少于3个的机器人[11]。数值法是将多个关节角组合代入到正向动力学方程,求解出机器人末端在任务空间的坐标,最终得到工作空间的方法,求解简单,适用于任意结构的机器人工作空间的求解[12]。
在数值方法中,求解机器人工作空间最为常见的方法就是蒙特卡洛方法。传统蒙特卡洛法的主要问题是工作空间点分布不均匀,大部分工作空间点产生在工作空间内部,导致工作空间边界求取精度不高,当提高工作空间点数量以提升工作空间边界求取精度时,大量工作空间点任然出现在工作空间内部,造成了计算资源的浪费,导致求解速度较慢。针对上述问题,徐振邦等利用蒙特卡洛法生成了一个种子工作空间,对于每个工作空间点数量较少的位置,在其内部选取一个参考点,在生成该点的关节角附近多次随机抽样并代入正向运动学方程,一次性得到多个工作空间点。这种方法使工作空间点云密度分布更加均匀,提高了工作空间边界处的精确度,但该方法的求解效率与分块数有关,需要根据具体的结构进行调整,并且拓展得到的工作空间点过于集中[13]。刘志忠等先利用蒙特卡洛法生成了一个种子空间,对种子空间分层,寻找每层的边界点,在边界点附近生成多个随机点,多次迭代,直到形成精确的边界。这种方法提高了工作空间边界处的精度,但求解精度依赖于分层数量,分层过少时精度不高,分层过多时消耗时间长[1]。
本文依托的国家重点研发计划“面向铸造行业的机器人智能化生产线研制及在航天装备与发动机关键部件制造上的示范应用”的一个研究任务是“设计多台面向铸造行业的机器人”,在初步确定机器人设计参数以后,需要对设计参数进行优化设计,优化设计过程中需要反复计算工作空间,因此有必要对机器人的工作空间求解方法进行改进。本文针对传统蒙特卡洛法求解精度低、求解速度慢的缺陷,提出了改进方法。利用传统蒙特卡洛法生成种子空间,拓展随机点数量较少的子空间,动态调整正态分布概率密度函数的参数,得到了可达工作空间。接着,利用可操作度评估了机器人的灵活性,从可达工作空间筛选出灵活种子空间,多次拓展灵活种子空间边界,并且正态分布标准差动态可调,得到了灵活工作空间。
1 研究对象及运动学模型
本文研究对象为湖南科技大学与长沙长泰机器人有限公司正在联合研制的6轴重载工业机器人,该机器人的6个关节均为转动关节,本体自重1 110 kg,负载能力210 kg,最大臂展2 674 mm,重复定位精度± 0.2 mm,具体结构如图1所示。
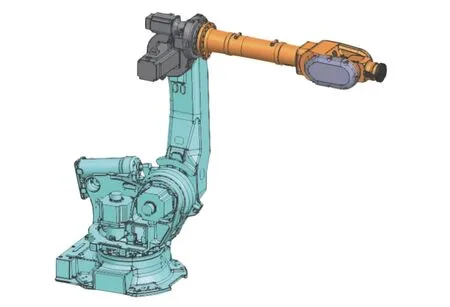
图1 6轴机器人结构示意图Fig.1 6-axis robot structure diagram
机器人运动学模型是求解机器人工作空间的基础,本文建立机器人连杆坐标系如图2所示,其中部分关节只表示了转轴的X轴和Z轴,对应的Y轴可根据右手定则求得。改进的D-H 参数表如表1所示,关节运动范围如表2所示,其中,ai代表连杆长度,di代表连杆偏移量,θi代表关节角,αi代表扭转角。

表2 6轴机器人关节运动范围Tab.2 Range of motion of 6-axis robot join
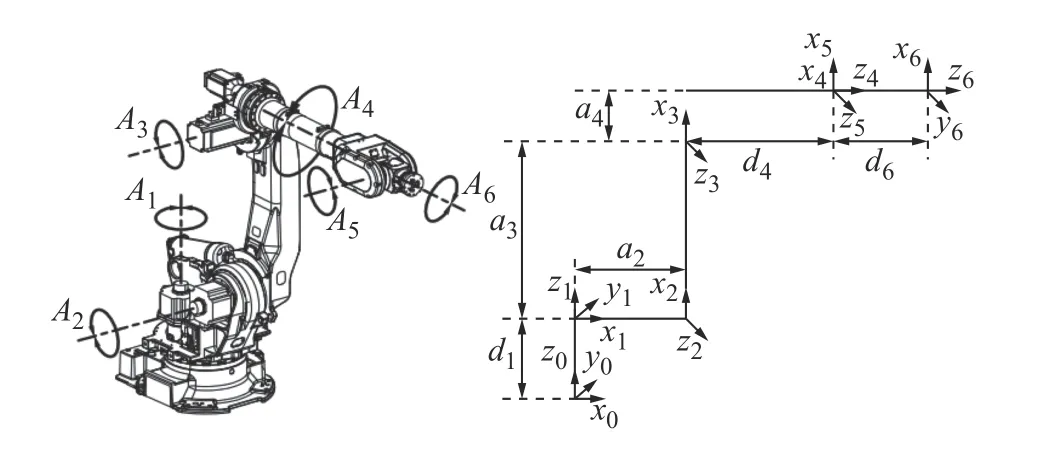
图2 6轴机器人坐标系Fig.2 6 axis robot coordinate system
相邻关节坐标系i-1和i之间的齐次变换矩阵为
式中:s=sin;c=cos。机械臂末端执行器的正向运动学方程为
式中:R为末端执行器坐标系相对与基坐标系的姿态矩阵;P为末端执行器在基坐标系中的位置向量。
2 可达工作空间分析
2.1 传统蒙特卡洛法
蒙特卡洛法是一种基于概率统计理论,用于模拟随机现象的数值方法。在求解机器人工作空间时,在各个关节角取值范围内随机抽取大量的关节角变量值进行组合,将这些关节角值组合带入正向运动学方程,计算出机器人末端执行器参考点的坐标值,这些参考点所包络的空间就是机器人工作空间。
传统蒙特卡洛法存在的问题如下:求解机器人工作空间时,工作空间边界的具体位置由工作空间边界的参考点给出,工作空间内部的点意义不大。然而,虽然传统蒙特卡洛法随机抽取的关节角值服从均匀分布,但关节空间到工作空间的映射是非线性的,大量工作空间点出现在工作空间内部,导致工作空间的精度不高。当增加随机抽取的关节角值组合的数量时,大部分参考点任然出现在非工作空间边界部分,虽然工作空间的精度变高,但大量的工作空间点没有意义,造成了计算资源的浪费。
2.2 方法的改进
根据上述分析,传统蒙特卡洛法的主要问题是工作空间点分布不均匀,大部分工作空间点产生在工作空间内部,导致工作空间边界求取精度不高的同时求解速度慢。针对上述问题,本文提出一种改进的蒙特卡洛法,该方法由3个部分组成。1)生成种子空间。利用传统蒙特卡洛法生成大量的工作空间点,用长方体包络所用种子空间点,划分成数个相等的子空间。2)拓展种子空间。筛选出需要拓展的子空间,利用正态分布抽样对这些子空间拓展,同时设置一个精度阈值确保拓展后的工作空间足够准确。为了保证拓展产生的点出现在边界附近,正态分布概率密度函数的方差会根据拓展后的点的位置进行调整。3)输出可达工作空间。多次重复拓展过程,直到每个子空间得到精确描述,输出可达工作空间。本文提出的改进蒙特卡洛法的具体步骤如下。
2.2.1 生成种子空间
用传统蒙特卡洛法对每一关节生成N个随机角度值,按序号组成对应关节角值组合。将关节角值组合代入正向运动学方程,求解出工作空间点在三维笛卡尔坐标系中的坐标值P(x,y,z),记录参考点在3个坐标轴方向的最大值和最小值,表示为Xmax,Ymax,Zmax和Xmin,Ymin,Zmin。
将所有工作空间点用长方体包络起来,由于种子空间位于实际工作空间之内,为了使实际工作空间位于长方体之内,确保拓展后的工作空间点都在种子空间内,将长方体的边长延长 ∆,求得能够包络实际工作空间的长方体,长方体的顶点坐标为
式中:l,w,h分别为长方体的长、宽、高。
将求得的长方体分别沿3个坐标轴方向分成nx,ny,nz等距部分,整个长方体被分成了k=nx×ny×nz个相等的子空间,根据每个子空间的位置进行编号,存储每个子空间内的工作空间点数量m,并存储每个工作空间点的位置信息以及关节角信息。
2.2.2 拓展种子空间
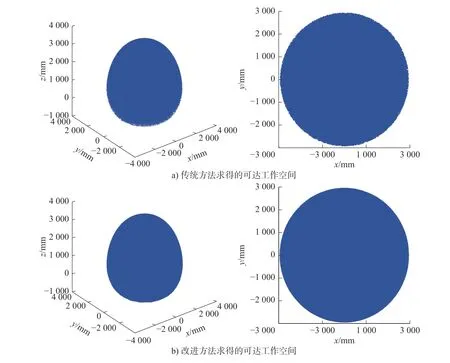
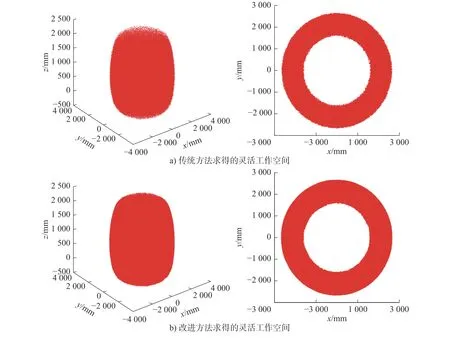
为了在提高可达工作空间边界求取精度时,减少计算资源的浪费,并且方便灵活工作空间的求解,应对每个工作空间点数量较少的子空间进行拓展。设置工作空间点数量阈值n,对每个子空间判断,若子空间内包含工作空间点并且工作空间点数量m 对每一个需要拓展的子空间i,随机抽取一个该子空间内部的工作空间点p,找到与该点对应的关节角值组合q。在关节角值组合q附近利用正态分布概率密度函数选取随机值,均值 µ=q,标准差σ初始值依据具体情况进行设定。取值后对新空间点的合理性进行判断,若关节角值组合q的每个关节角值都在该关节角的取值范围内,则保留该取值;若不满足,则舍弃该次取值并重新取值。将取得的关节角值组合q′代入正向运动学方程,产生一个新的工作空间点p′,并存储新生成工作空间点p′的位置信息和关节角信息。为了使得每个本应存在工作空间点的子空间均得到拓展,计算出工作空间点p′所在的子空间ic,读取子空间ic的工作空间点数量mc,对其进行判断,若mc=0,则将子空间存入列表L。为了避免拓展后的工作空间点集中出现在一个工作空间点附近,每拓展一次后进行判断,若该子空间中的工作空间点数量小于阈值n,则重新在该子空间中的工作空间点中任意抽取一个点p,重复拓展过程,直到该子空间中的工作空间数量大于阈值n。 由于部分子空间与实际工作空间的交集较小,在拓展这一类子空间时,新生成的点p′虽然大部分出现在被拓展点p附近,却出现在被拓展点p所在的子空间之外,导致该子空间附近的子空间产生大量的工作空间点,造成了计算资源的浪费。同时,部分位于关节角范围边界处的关节角值组合q,在产生新的关节角值组合q′时,q′常常出现在关节角取值范围外,需要重新取值,造成了资源的浪费。为了减少上述的计算资源的浪费,需要根据新生成的关节角值q′和工作空间点p′的位置调整正态分布的方差 σ。用nf代表拓展时新生成的关节角值在对应关节角取值范围外的次数,用nl代表拓展时新生成的工作空间点出现在被拓展点p所在子空间外的次数,当nf大于临界值时,表明正态分布方差 σ过大,将正态分布方差 σ除以一个大于1的数 δ以缩小方差 σ,方差σ 调整后,将nf置零;当nl大于临界值时,表明该子空间与实际工作空间的交集较小,将正态分布方差 σ除以一个大于1的数δ 以缩小方差 σ,方差 σ调整后,将nl置零。每拓展完一个子空间后,nf、nl置零。 2.2.3 输出可达工作空间 列表L中的子空间全部拓展后,每个子空间已得到精确描述,得到可达工作空间,输出储存的点的位置信息。改进方法的整体流程框图如图3所示。 图3 可达工作空间求解流程图Fig.3 Reachable workspace solution flow chart 求解机器人灵活工作空间,首先需要对机器人的灵活性进行评估。机器人灵活性评估指标主要有最小奇异值、条件数和可操作度[14]。其中,最小奇异值和条件数只考虑了机器人末端执行器在某一位置的特定方向上的灵活性,而可操作度指标则考虑了机器人末端执行器在该位置上每个方向的灵活性[15]。因此,本文利用可操作度指标评价机器人的灵活性。 可操作度的定义由Yoshikawa 给出[16]。对于一个n自由度的机器人,其末端运动学微分方程为 可操作度是对机器人在某一位行下的各方向灵活性的综合度量,可操作度越大,灵活性越好,当可操作度为0时,机器人雅克比矩阵不可逆,机器人处于奇异位行。 灵活工作空间求解分为3个阶段,第一阶段生成灵活种子空间,第二阶段拓展灵活种子空间,第三阶段输出灵活工作空间。 第一阶段:求解得到可达工作空间,对每个工作空间点进行灵活性评估,求得每个点对应的可操作度值 ω,筛选出最大可操作度值 ωm,记录产生该位姿的关节角组合qm。利用正态分布在关节角组合qm附近取随机值组合qm′,计算与关节角组合随机值qm′对应的可操作度值 ω′,对 ω′进行判断,若 ω′大于最大可操作值 ωm,则将由该关节角组合qm′生成的工作空间点信息取代由qm所生成的工作空间点信息,否则,舍弃本次取值。若新产生可操作值 ω′共有a(a为一常数,依据具体情况设定)次小于最大可操作值 ωm,则说明当前求得的最大可操作值 ωm已十分接近实际最大值,终止本次计算。设置可操作度阈值为 式中 γ为一个小于1的常数。以可操作度阈值 ωc为分界点,将可操作度大于 ωc的工作空间空间点被定义为灵活工作空间点,筛选出灵活工作空间点,生成灵活种子空间。 第二阶段:采用本文所述的改进蒙特卡洛法对种子空间进行选取和拓展。与求解可达工作空间不同之处在于:1)在筛选需要拓展的子空间时,增加一个判定条件,若该子空间周围的26个子空间中存在工作空间点数量为零的子空间,即该子空间为边界空间时,将该空间编号存入列表L,否则,舍弃该编号。2)在存储新生成的工作空间点的判断中,加入新的约束,若由新生成点p′生成的的可操作度 ω′大于 ωc,则存储;否则舍弃。 第三阶段:列表L中的子空间全部拓展后,工作空间边界求取足够精确,得到灵活工作空间,输出灵活工作空间。改进方法总体流程如图4所示。 图4 灵活工作空间求解流程图Fig.4 Flexible workspace solution flow chart 对本文研究对象,分别用传统蒙特卡洛法和本文所述的改进蒙特卡洛法在MATLAB 编程,进行工作空间求解仿真,并利用MATLAB 中的拟合函数求解工作空间体积。当工作空间点数量为1.5×106时,用传统蒙特卡洛法求解的工作空间如图所示。当采用本文所示的改进蒙特卡洛法求解工作空间时,各参数设置如表3所示,得到的可达工作空间如图5所示,最终得到的工作空间点数量为1 299 133个。 表3 改进蒙特卡洛法参数设置Tab.3 Improved Monte Carlo method parameter Settings 图5 机器人可达工作空间Fig.5 Robots can reach the workspace 对比两种方法求解出的工作空间,可以得到以下结论:当工作空间点数量大致相同时,采用传统蒙特卡洛法求得的工作空间点大部分出现在工作空间内部,得到的工作空间边界求取精度低,采用本文所述的改机蒙特卡洛法求得的工作空间点分布均匀,得到的工作空间边界求取精度高。 通过不断增加传统蒙特卡洛法的随机工作空间点数量,使求解得到的工作空间越来越接近实际工作空间。用生成的工作空间体积变化表示工作空间的变化,逐渐增加工作空间点数量,工作空间的体积随工作空间点数量增加的变化如表4所示,当工作空间点数量达到 2×107时,体积变化不再明显,体积为75.238 m3。采用改进方法求解,当体积达到75.356 m3时,仅需要 1 .2991×106个工作空间点,所需参考点仅是传统方法的6.49%。 表4 可达工作空间体积随工作空间点变化表Tab.4 Reachable workspace volume change table with workspace points 采用本文所述的方法求解灵活工作空间,当参数设置如表3所示,同时 γ=0.8、a=1 500时,求解的灵活工作空间如图6所示,工作空间点数量为718 324,最大可操作值 ωm=3.01,求解的灵活工作空间体积为24.929 m3。 图6 机器人灵活工作空间Fig.6 Flexible workspace for robots 不断增加传统蒙特卡洛法的随机工作空间点数量,当工作空间点数量达到 5×106附近后,继续增加工作空间点数量时,最大可操作值 ωm几乎不再变化,最大可操作值 ωm=3.01。利用传统方法求解的工作空间点数量为 2×107的可达工作空间计算灵活工作空间,筛选出的灵活工作空间点数量为611 749,求解的灵活工作空间体积为23.625 m3。灵活工作空间如图6所示。 上述结果表明:当利用十分精确的可达工作空间计算灵活工作空间时,改进方法求解得到的工作空间点数量与传统方法相近,最大可操作值 ωm十分接近实际最大可操作度值,灵活工作空间体积更为精确,灵活工作空间体积相对提高了 5.52% 。 1)分析了在设计过程中求解机器人工作空间的传统蒙特卡洛法存在的问题。传统蒙特卡洛法随机点分布不均,大量随机点出现在工作空间内部,降低求解精度的同时还造成了计算资源的浪费。 2)针对上述问题,以6轴机器人为对象,提出了一种基于蒙特卡洛法的工作空间求解方法。生成种子空间并划分成多个子空间,对工作空间点数量较少的的子空间进行拓展,根据拓展后工作空间点的位置调整随机函数的参数,确保了新产生的点位于工作空间边界附近,多次拓展,使工作空间足够精确,得到可达工作空间。仿真结果表明:当求得工作空间十分精确时,改进蒙特卡洛法所需的工作空间点数量仅是传统方法的 6.50% 。 3)在可达工作空间求解方法的基础上提出了灵活工作空间的求解方法。利用可操作度概念评估机器人的灵活性,从可达工作空间筛选出灵活种子空间,利用可调参数的正态分布多次拓展灵活种子空间边界,直到边界足够精确,得到灵活工作空间。仿真结果表明:当利用十分精确的可达工作空间计算灵活工作空间时,改进方法和传统方法求解得到的工作空间点数量相近,但求解得到的灵活工作空间体积更为精确,体积较传统方法提高了5.52%。 4)本文提出的基于蒙特卡洛法的机器人工作空间求解方法能够用于机器人工作空间的求解,并且能在保证求解精度的前提下可极大的提升求解效率,为后续的机器人优化设计提供了便利。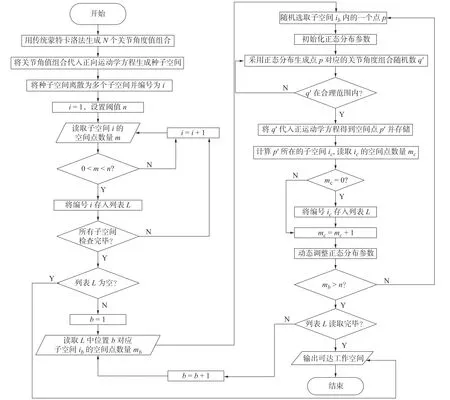
3 灵活工作空间分析
3.1 机器人可操作度分析
3.2 灵活工作空间求解方法
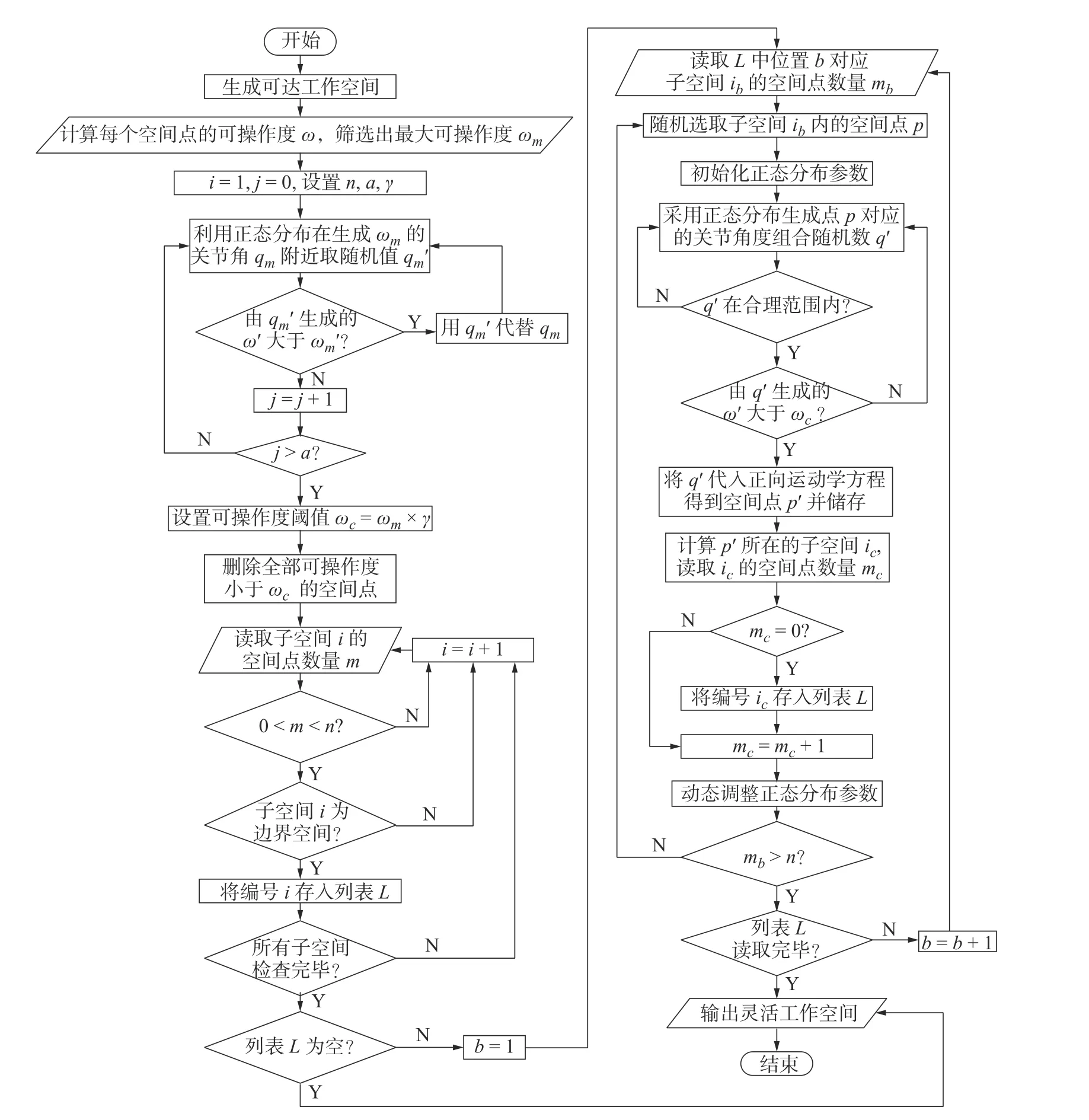
4 求解实例
4.1 可达工作空间求解
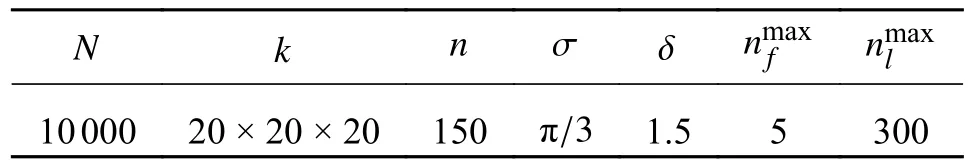

4.2 灵活工作空间求解
5 结论

